MathProf - Rotationsparaboloid - Rotationskörper - Paraboloid

Fachthema: Rotationsparaboloid - Volumen

MathProf - Analysis - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Veranschaulichung des Prinzips der Ermittlung der Volumina von Rotationskörpern (Herleitung) am Beispiel eines Paraboloids.

Ein frei bewegbares und drehbares, dreidimensionales Koordinatensystem erlaubt die Durchführung interaktiver Analysen bzgl. Sachverhalten und relevanter Zusammenhänge zu diesem Fachthema.

 

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.
 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

 

Themen und Stichworte zu diesem Modul: Paraboloid - Drehparaboloid (Rotationskörper) - Volumen

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.
 

 

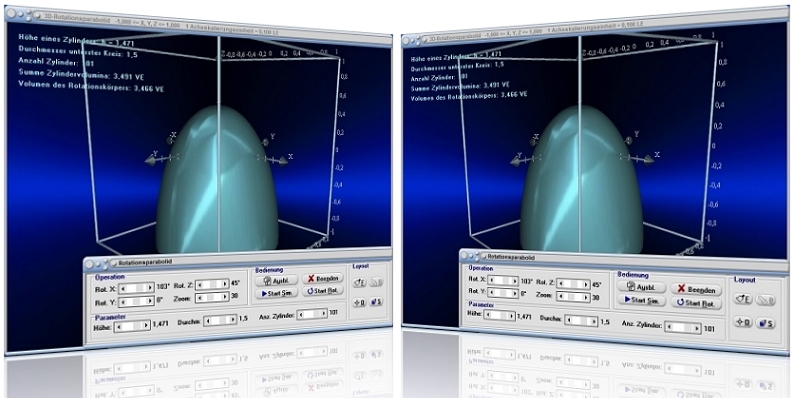
Modul Rotationsparaboloid

 
Im kleinen Unterprogramm [Analysis] - [Integrationsverfahren] - Rotationsparaboloid kann das Prinzip zur Ermittlung der Volumina von Rotationskörpern am Beispiel eines Rotationsparaboloids untersucht werden.

Um derartige Volumina errechnen zu können, wird der Rotationskörper in eine bestimmte Anzahl von Scheiben (Zylinder) gleicher Dicke zerlegt. Je größer die Anzahl verwendeter Scheiben und je geringer somit die Dicke der Scheiben wird, desto genauer kann das exakte Volumen eines Körpers bestimmt werden. Durch eine Aufsummierung der Volumina der einzelnen Scheiben kommt man zum Ergebnis.

Positionieren Sie die auf dem Bedienformular zur Verfügung stehenden Schieberegler Höhe, Durchm. und Anz. Zylinder, durch welche Sie die Höhe und den Durchmesser des Paraboloids, sowie die Anzahl zu verwendender Zylinder einstellen können.

Bei jeder Veränderung einer Rollbalkenposition werden die Ergebnisse durchgeführter Berechnungen ausgegeben. Das Programm ermittelt hierbei die Summe der Zylindervolumina (Summe Zylindervolumina) in Abhängigkeit von der Anzahl verwendeter Zylinder (Anzahl Zylinder) und stellt diese dem wahren Wert des Volumens des Rotationskörpers gegenüber (Volumen des Rotationskörpers).

Durch eine Bedienung der Schaltfläche Start Sim. kann eine Simulation gestartet werden. Die Schaltfläche trägt hierauf die Bezeichnung Stop Sim. Angehalten werden kann die Simulation durch eine erneute Betätigung dieser.

Vor dem Start einer Simulation wird ein Formular zur Verfügung gestellt, auf welchem Sie durch Aktivierung der entsprechenden Kontrollkästchen die Auswahl zu simulierender Parameter treffen.

Hinweis:

Die Geschwindigkeit zur Durchführung einer Rotationssimulation können Sie verändern, indem Sie den Schalter O auf dem Bedienformular betätigen und auf dem Einstellungsformular im Formularbereich Rotationsgeschwindigkeit den Rollbalken Verzögerung positionieren (voreingestellt: 160).

Um diesen Wert zu speichern, aktivieren Sie auf dem Einstellungsformular das Kontrollkästchen Eingest. Optionen speichern und bedienen die Schaltfläche OK. Die Speicherung dieses Werts erfolgt fachthemenbezogen, nicht unterprogrammbezogen.

Beim Aufruf von Beispielen mit Rotationssimulation verwendet das Programm den unter Globale Optionen - 3D-Beispiele eingestellten, und nicht den mit Hilfe des Rollbalkens Verzögerung voreingestellten, Wert!
 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
 

Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.

Integrationsmethoden

Integration

Integration mit Funktion in expliziter Form - Rotation um x-Achse

Integration mit Funktion in expliziter Form - Rotation um y-Achse

Werden die Rollbalken auf dem Bedienformular wie folgt positioniert:

Höhe: h = 0,725

Durchmesser des untersten Kreises: d = 1,5

Anzahl dargestellter Zylinder: 20

so ermittelt das Programm:

Die Summe der Volumina der dargestellten Zylinder beträgt 1,77 VE. Das (wahre) Volumen des Rotationskörpers beträgt 1,708 VE.
 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2
 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Rotationsparaboloid zu finden. 

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

MathProf 5.0 - Unterprogramm Flächen 2. Ordnung

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

Unsere Produkte

 
Nachfolgend aufgeführt finden Sie Kurzinfos zu den von uns entwickelten Produkten.

 

I - MathProf 5.0
Mathematik interaktiv
 

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.
 

 

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
 

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Analysis
• Kurzinfos zum Themengebiet Geometrie
• Kurzinfos zum Themengebiet Algebra
• Kurzinfos zum Themengebiet 3D-Mathematik
• Kurzinfos zum Themengebiet Stochastik
• Kurzinfos zum Themengebiet Vektoralgebra
• Kurzinfos zum Themengebiet Trigonometrie
• Kurzinfos zu sonstigen Themengebieten

---

 

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in MathProf implementierten Modulen finden Sie, indem Sie den Reiter MathProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 

II - PhysProf 1.1
Physik interaktiv
 

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.
 

 

Durch die Benutzung dieses Programms wird es ermöglicht, bereits bekannte Fachthemeninhalte aufzuarbeiten und entsprechende Sachverhalte numerisch wie auch grafisch zu analysieren. Mittels der freien Veränderbarkeit der Parameter von Einflussgrößen bei der Ausgabe grafischer Darstellungen besteht in vielen Unterprogrammen die Möglichkeit, Veränderungen an dargestellten Zusammenhängen manuell oder durch die Anwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
 

Eine Übersicht aller in PhysProf 1.1 zur Verfügung stehender Programmteile finden Sie im PhysProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Kurzinfos zu Inhalten einiger Unterprogramme von Physprof 1.1 erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Mechanik
• Kurzinfos zum Themengebiet Elektrotechnik
• Kurzinfos zum Themengebiet Optik
• Kurzinfos zum Themengebiet Thermodynamik
• Kurzinfos zu sonstigen Themengebieten

---

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in PhysProf implementierten Modulen finden Sie, indem Sie den Reiter PhysProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
 

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

 

 
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
 

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

---

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.