PhysProf - Durchschnittsgeschwindigkeit - Geschwindigkeit - Weg - Zeit

Fachthemen: Bewegung und Geschwindigkeit
PhysProf - Kinematik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Durchführung von Untersuchungen zur Bewegungslehre bzgl. des Richtungsverhaltens von Geschwindigkeiten in der Ebene.
Dieses Teilprogramm ermöglicht die Praktizierung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte. Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul: |
 |  |
Bewegung und Geschwindigkeit
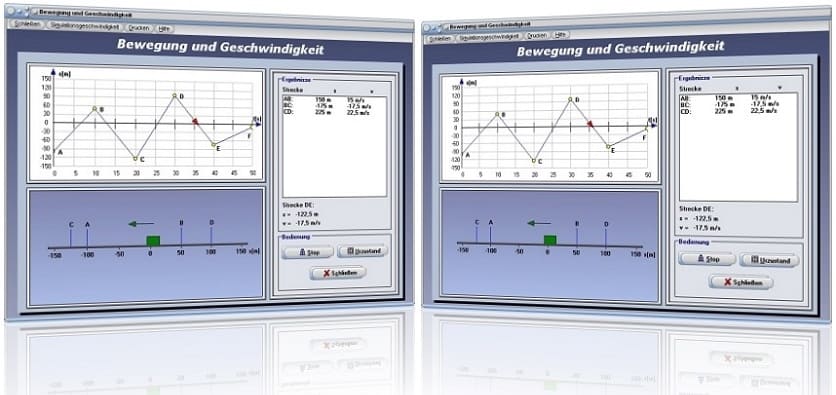
Modul Bewegung und Geschwindigkeit
Mit Hilfe des Unterprogramms [Mechanik I] - [Bewegung und Geschwindigkeit] können Untersuchungen bzgl. des Richtungsverhaltens von Geschwindigkeiten in der Ebene durchgeführt werden.

Bewegung - Geschwindigkeit - Abbildung 1

Bewegung - Geschwindigkeit - Abbildung 2
Die Geschwindigkeit beschreibt, in welcher Zeit und in welcher Richtung ein Körper während dem Lauf der Zeit seine Position ändert.
Als Momentangeschwindigkeit wird die innerhalb eines (kurzen) Zeitintervalls zurückgelegte Strecke Δs (Δx) dividiert durch durch das Zeitintervall Δt bezeichnet. Geometrisch kann die momentane Geschwindigkeit beim Ablauf einer gleichförmigen Translation aus folgendem Zusammenhang gedeutet werden:

Hierbei sind:
v: Momentane Geschwindigkeit [m/s]
x1: Zurückgelegter Weg zur Zeit t1 [m]
x2: Zurückgelegter Weg zur Zeit t2 [m]
t1,t2: Zeit [s]
Findet die Bewegung von einem kleineren X-Wert zu einem größeren statt, so besitzt die Geschwindigkeit einen positiven Wert. Findet sie hingegen in umgekehrter Richtung statt, so erhält sie ein negatives Vorzeichen.
Bewegt sich ein Körper von unten nach oben, so wird die Geschwindigkeit als positiv, bewegt er sich hingegen von oben nach unten, als negativ betrachtet. Allgemein gilt: Eine negative Geschwindigkeit liegt vor, wenn diese einen negativen Zahlenwert (< 0) annimmt. Eine positive Geschwindigkeit ergibt sich bei einem Zahlenwert > 0 für diese.
Eine zusammengesetzte Bewegung ist eine Bewegung, die sich aus mehreren Bewegungsformen zusammensetzt. Diese können unterschiedlicher Art sein. Zwei Fachthemengebiete die sich mit der Bewegung auseinandersetzen sind die Kinematik (Lehre der Beschreibung der Bewegung) sowie die Dynamik (Kinetik), die als Lehre der Ursachen von Bewegung bezeichnet wird.
Als Bewegungsgleichung wird eine Funktionsgleichung bezeichnet, die die zeitliche Entwicklung und die Bewegung eines Körpers im Raum bzw. eines mechanischen Systems vollständig beschreibt.
Als Bewegungsänderung kann die Beschleunigung sowie das Bremsen angesehen werden.
Mit einem Weg-Zeit-Diagramm wird der durch einen bewegten Körper zurückgelegte Weg zeitabhängig grafisch dargestellt. Ein derartiges Diagramm wird in diesem Modul für eine zusammengesetzte Bewegung ausgegeben und kann analysiert werden.
Programmbedienung
Einige der oben beschriebenen Sachverhalte können Sie in diesem Programmmodul untersuchen. Bedienen Sie die Schaltfläche Start, so wird der aufgezeichnete Bewegungsablauf von einem Pfeil durchlaufen, welcher die Richtungsorientierung der Geschwindigkeit vektoriell darstellt.
Synchron zu diesem Ablauf wird im unteren Diagramm die momentane Richtung der Geschwindigkeit der ablaufenden Bewegung dargestellt und nach dem Erreichen eines Punktes, ab welchem ein Richtungswechsel eintritt, werden die entsprechenden Werte ausgegeben. Mit Hilfe des Schalters Urzustand können Sie die grafische Darstellung wieder in den Anfangszustand versetzen.
Die mittlere Geschwindigkeit (Durchschnittsgeschwindigkeit oder durchschnittliiche Geschwindigkeit) beschreibt die Geschwindigkeit, die ein Objekt besessen hätte, wenn dieses über einen bestimmten Zeitraum hinweg mit gleichmäßiger Geschwindigkeit bewegt worden wäre.
1. Ohne Anfangsgeschwindigkeit
Die mittlere Geschwindigkeit (Durchschnittsgeschwindigkeit) einer gleichförmig (gleichmäßig) beschleunigten geradlinigen Bewegung ohne Anfangsgeschwindigkeit kann wie folgt berechnet werden:
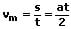
vm: Mittlere Geschwindigkeit [m/s]
s: Zurückgelegter Weg [m]
a: Beschleunigung [m/s²]
t: Zeit [s]
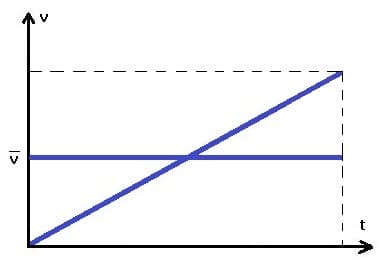
Mittlere Geschwindigkeit ohne Anfangsgeschwindigkeit: vt-Diagramm
2. Mit Anfangsgeschwindigkeit
Bei einer beschleunigten geradlinigen Bewegung mit Anfangsgeschwindigkeit gilt für die Durchschnittsgeschwindigkeit:
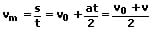
vm: Mittlere Geschwindigkeit [m/s]
v0: Anfangsgeschwindigkeit [m/s]
v: Geschwindigkeit zur Zeit t [m/s]
s: Zurückgelegter Weg [m]
a: Beschleunigung [m/s²]
t: Zeit [s]
Gilt es, ein zeitliches Intervall einer solchen Bewegung unter der Berücksichtigung des bereits zurückgelegten Weges s0 zu berechnen, so kann dies wie nachfolgend gezeigt erfolgen:
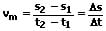
vm: Mittlere Geschwindigkeit [m/s]
t1,t2: Zeit [s]
s1: Zurückgelegter Weg zur Zeit t1 [m]
s2: Zurückgelegter Weg zur Zeit t2 [m]
Δt: Zeitdauer [s]
Δs: Zurückgelegter Weg [m]
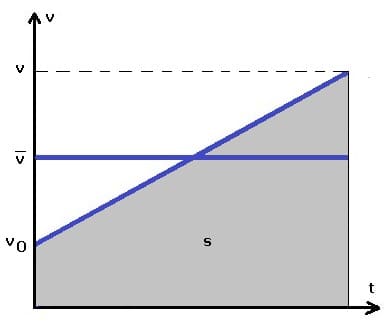
Mittlere Geschwindigkeit mit Anfangsgeschwindigkeit: vt-Diagramm
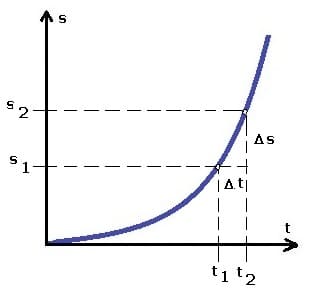
Mittlere Geschwindigkeit mit Anfangsgeschwindigkeit: st-Diagramm
Der Zeitmittelwert (oder zeitlicher Mittelwert) ist der Durchschnitt (das arithmetische Mittel) eines Anfangs- und Endwerts einer Zeitperiode. Er wird mittels nachfolgend gezeigter Formel beschrieben:

f(t): Zeitlicher Mittelwert [s]
f: zeitabhägige Funktion [s]
Δt: Dauer des Intervalls [s]
t: Zeit [s]
Körper können Bewegungen ausführen, die sich aus mehreren Teilbewegungen zusammensetzen. Dieser Fall wird als Überlagerung von Bewegungen oder Superposition bezeichnet. Diese Tatsache wird auch Superpositionsprinzip oder Unabhängigkeitsprinzip genannt.
Werden von einem Körper gleichzeitig zwei oder mehrere Teilbewegungen ausgeführt, so überlagern sich diese unabhängig voneinander und es resultiert eine überlagerte Bewegung. Hierbei addieren sich die einzelnen Wege, Geschwindigkeiten und Beschleunigungen in vektorieller Form. Einzelne Teilbewegungen können in gleicher oder in beliebiger anderer Richtung zueinander erfolgen.
Es gilt für den Weg s, die Geschwindigkeit v und die Beschleunigung a:



Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Gleichförmige Bewegung sowie unter Wikipedia - Bewegung zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
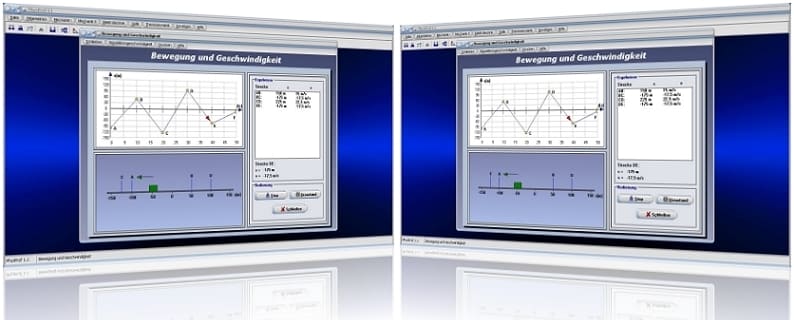
Unterprogramm Bewegung und Geschwindigkeit

PhysProf 1.1 - Unterprogramm RLC-Kreis

MathProf 5.0 - Unterprogramm Kurven in Parameterform

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















