MathProf - Platonische Körper - Dodekaeder - Regelmäßige Polyeder

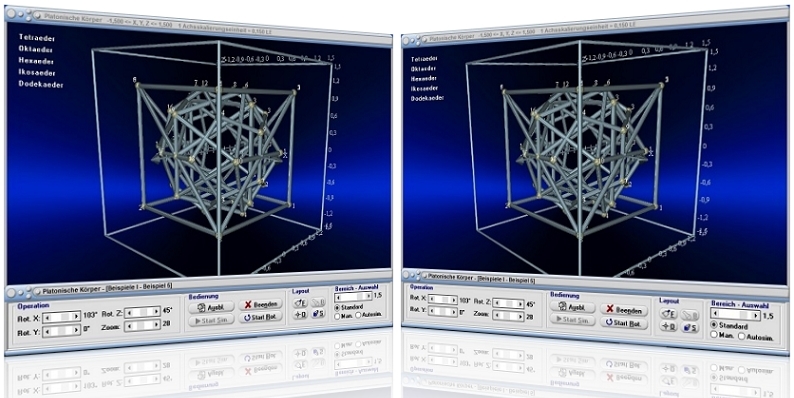
Modul Platonische Körper

---

 

Das Unterprogramm [Geometrie] - Platonische Körper ermöglicht die Berechnung, sowie die dreidimensionale räumliche Darstellung Platonischer Körper.

 

Im dreidimensionalen Raum existieren lediglich exakt fünf regelmäßige Polyeder, die von untereinander kongruenten (deckungsgleichen) Vielecken begrenzt werden. Dieser Sachverhalt ist seit der Antike bekannt. Diese Polyeder werden als platonische Körper bezeichnet. Regelmäßig bedeutet in diesem Zusammenhang, dass keine Ecke und keine Fläche des Gebildes herausgehoben ist. Die platonischen Körper sind die Polyeder die über größtmögliche Symmetrie verfügen.
 
Nachfolgend aufgeführt sind einige besondere Regelmäßigkeiten platonischer Körper:

 - all ihre Flächen besitzen die gleiche Anzahl an Ecken
 - all ihre Kanten besitzen die gleiche Länge
 - all ihre Winkel sind gleich groß
 - in all ihren Ecken stößt die selbe Anzahl an Kanten zusammen

Inkugel - Umkugel: Jeder platonische Körper verfügt über eine Symmetrie, die es ermöglicht eine Inkugel sowie eine Umkugel zu konstruieren. Die Inkugel berührt jede seine Flächen innenseitig. Seine Umkugel berührt jede seiner Ecken.

Dualität: Werden alle benachbarten Seitenmitten eines platonischen Körpers miteinander verbunden, so entsteht hierdurch ein innerer Körper, der wiederum selbst ein platonischer Köper darstellt. Ein Tetraeder ist zu sich selbst dual.

Die fünf platonischen Körper sind:
 

• Tetraeder (Vierflächner - Dreiseitige Pyramide)

• Oktaeder (Achtflächner)

• Hexaeder (Sechsflächner, Würfel)

• Ikosaeder (Zwanzigflächner)

• Dodekaeder (Zwölfflächner) 

 
Ein Tetraeder ist ein regelmäßiges Polyeder, welches vier gleichseitige Dreiecke als Seitenflächen besitzt und über sechs Kanten gleicher Länge verfügt. Ein reguläres Tetrader wird auch als dreiseitige Pyramide bezeichnet. Es hat vier Ecken.

Ein Hexaeder (Würfel) ist ein Körper, welcher sechs kongruente Quadrate als Seitenflächen besitzt und über zwölf Kanten gleicher Länge verfügt. Es hat acht Ecken.

Ein Oktaeder ist ein regelmäßiges Polyeder, welches acht kongruente Dreiecke als Seitenflächen besitzt und über zwölf Kanten gleicher Länge verfügt. Es hat sechs Ecken.

Ein Dodekaeder ist ein regelmäßiges Polyeder, welches 12 kongruente Fünfecke als Seitenflächen besitzt und über dreißig Kanten gleicher Länge verfügt. Es hat zwanzig Ecken.

Ein Ikosaeder ist ein regelmäßiges Polyeder, welches 30 Dreiecke als Seitenflächen besitzt und über zwölf Ecken verfügt, in welchen sich je fünf Seitenflächen berühren. Es hat zwölf Ecken.


Das Programm ermittelt bei der Ausführung von Berechnungen für den entsprechenden Körper in Abhängigkeit von der eingegebenen Kantenlänge:

• Volumen
• Oberfläche
• Inkugelradius
• Kantenkugelradius
• Umkugelradius
• Anzahl der Ecken
• Anzahl der Kanten
• Anzahl der Flächen (Vielecke)
• Kanten pro Fläche
• Kanten pro Ecke
• Winkel zwischen zwei Flächen

  

 
Der Eulersche Polyedersatz besagt: Bei jedem konvexen Polyeder mit e Ecken, f Flächen und k Kanten gilt: e + f - k = 2.
 
Dies bedeutet: Werden alle Ecken und Flächen eines Polyeders zusammengezählt und wird hiervon die Anzahl der kanten des Polyeders abgezogen, so resultiert stets die Zahl 2. Dies gilt in jedem aller möglichen Fälle!
 
Beispiel Ikosaeder:

Anzahl Ecken: 12
Anzahl Flächen: 12
Anzahl Kanten: 30
Es gilt: e + f - k = 2 -> 12 + 20 - 30 = 2
 

 
Nachfolgend aufgeführt sind Formeln, die zur Berechnung der Werte entsprechender Größen des entsprechenden platonischen Körpers benötigt werden.
 

Tetraeder:

Höhe: h = √6·a / 3
Oberfläche: A = √3·a²
Volumen: V = √2·a³ / 12
Radius der Umkugel: r_u = √6·a / 4
Kantenkugelradius: r_k = √2·a / 4
Radius der Inkugel: r_i = √6·a / 12
 
Oktaeder:

Oberfläche: A = 2·√3·a²
Volumen: V = √2·a³ / 3
Radius der Umkugel: ru = √2·a / 2
Kantenkugelradius: rk = a / 2
Radius der Inkugel: r_i = √6·a / 6

Hexaeder:

Oberfläche: A = 6·a²
Volumen: V = a³
Radius der Umkugel: r_u = √3·a / 2
Kantenkugelradius: rk = √2·a / 2
Radius der Inkugel: r_i = a / 2

Ikosaeder:

Oberfläche: A = 5·√3·a²
Volumen: V = 5/12·a³·( 3 + √5)
Radius der Umkugel: r_u = √10 + 2·√5·a / 4
Kantenkugelradius: rk = ( 1 + √5 )·a / 4
Radius der Inkugel: r_i =  a / 12·√3 /( 3 + √5 )

Dodekaeder:

Oberfläche: A = 3·a²·√25 + 10·√5
Volumen: V = a³ / 4·(15+  7 + √5)
Radius der Umkugel: r_u = √1 + √5·a / 4·√3
Kantenkugelradius: r_k = ( 3 + √5 )·a / 4
Radius der Inkugel: r_i =  √(25 + 11·√5)/10·a / 2

Mit:
a: Kantenlänge
 

Nachfolgend aufgeführt ist eine Übersicht, die Auskunft über die Anzahl der Ecken, Kanten und Fläche einzelner platonischer Körper gibt.
 

Körper	f	n	e	m	k
Tetraeder	4	3	4	3	6
Hexaeder	6	4	8	3	12
Oktaeder	8	3	6	4	12
Dodekaeder	12	5	20	3	30
Ikosaeder	20	3	12	5	30

mit:
e: Anzahl der Ecken
f: Anzahl der Flächen
k: Anzahl der Kanten
m: Anzahl der Kanten je Ecke
n: Anzahl der Vieleckseiten je Kante

Begrenzungsflächen:

Tetraeder: 4 gleichseitige Dreiecke
Oktaeder: 8 gleichseitige Dreiecke
Ikosaeder: 20 gleichseitige Dreiecke
Hexaeder: 6 Quadrate
Dodekaeder: 12 regelmäßige Fünfecke
   
 

 

Grafische Darstellung - Beispiel 1 - Dodekaeder


Grafische Darstellung - Beispiel 2 - Hexaeder


Grafische Darstellung - Beispiel 3 - Ikosaeder


Grafische Darstellung - Beispiel 4 - Oktaeder


Grafische Darstellung - Beispiel 5 - Tetraeder
 

Bei der Kantenkugel handelt es sich um eine Kugel, die alle Kanten des gegebenen Polyeders berührt. Die Inkugel eines Polyeders ist die Kugel, die alle Flächen des gegebenen Polyeders berührt. Die Kugel auf der alle Ecken des gegebenen Polyeders liegen, wird als Umkugel bezeichnet.
 

Berechnung und Darstellung

 
Gehen Sie folgendermaßen vor, um Berechnungen mit Platonischen Körpern (regulären Polyedern) durchzuführen und sich diese darstellen zu lassen:
 

1. Selektieren Sie durch die Aktivierung des entsprechenden Kontrollschalters (Tetraeder, Hexaeder, Oktaeder ...) den Körper mit dem Berechnungen durchzuführen sind.
    
2. Geben Sie den Wert der Kantenlänge des Polyeders in das dafür vorgesehene Feld ein.
    
3. Nach einer Bedienung der Schaltfläche Berechnen werden die Ergebnisse in der dafür zur Verfügung stehenden Listbox ausgegeben.
    
4. Wählen Sie mit Hilfe der aufklappbaren Auswahlbox Auswahl die Art, wie Sie Körper dargestellt bekommen möchten. Hierzu stehen die weiter unten aufgeführten Möglichkeiten zur Verfügung.
   
   Bei Wahl einer Rohr- oder Liniengitterdarstellung kann durch die Aktivierung der daraufhin benutzbaren Kontrollkästchen Tetraeder, Oktaeder, Hexaeder, Ikosaeder oder Dodekaeder bestimmt werden, welche der Körper in Form von Draht- bzw. Rohrgittermodellen (gemeinsam) dargestellt werden sollen.
    
5. Legen Sie durch die Aktivierung des entsprechenden Kontrollschalters (Ohne Kugel, Inkugel, Kantenkugel, Außenkugel) fest, ob lediglich die Darstellung des Körpers erfolgen soll, oder ob dessen In-, Kanten- bzw. Außenkugel ebenfalls grafisch ausgegeben werden soll.
    
6. Klicken Sie auf die Schaltfläche Darstellen.

 
Die Ausgabe der grafischen Darstellung kann auch durch Ausführung eines Doppelklicks auf einen entsprechenden Eintrag in der linksseitig angeordneten Tabelle eingeleitet werden.

 
 

  

Im Formularbereich Darstellung können Sie durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende Einstellungen vornehmen, die bei Ausgabe der grafischen Darstellung der Zusammenhänge wirksam werden:
 

• Punkte: Darstellung der Eckpunkte des Körpers ein-/ausschalten

• Punkte als Kugeln: Darstellung der Eckpunkte des Körpers als (kleine) Kugeln ein-/ausschalten

• Punkte beschriften: Beschriftung der Eckpunkte des Körpers ein-/ausschalten

Durch die Bedienung der aufklappbaren Auswahlbox in diesem Formularbereich werden zudem folgende Optionen zur Verfügung gestellt, das Layout eines dargestellten Körpers zu beeinflussen:
 

• Gefüllt - Kanten als Rohre einzeln: Darstellung der Körperkanten als Rohre, inkl. der Füllung von Flächen

• Gefüllt - Kanten als Linien einzeln: Darstellung der Körperkanten als Linien, inkl. der Füllung von Flächen

• Gefüllt - Ohne Kantenmarkierung einzeln: Darstellung der Körperkanten, ohne Begrenzungsmarkierung und ohne die Füllung von Flächen

• Rohrgitterdarstellung einzeln: Darstellung eines einzelnen Körpers in Form eines Rohrgittermodells, ohne die Füllung von Flächen (Körpernetz)

• Liniengitterdarstellung einzeln: Darstellung eines einzelnen Körpers in Form eines Liniengittermodells, ohne die Füllung von Flächen (Körpernetz)

• Rohrgitterdarstellung mehrfach: Gleichzeitige Darstellung eines, oder mehrerer Körper in Form von Rohrgittermodellen, ohne die Füllung von Flächen (Körpernetz)

• Liniengitterdarstellung mehrfach: Gleichzeitige Darstellung eines, oder mehrerer Körper in Form von Liniengittermodellen, ohne die Füllung von Flächen (Körpernetz)

  

 

 

In diesem Unterprogramm besteht die Möglichkeit, sich Darstellungen auf folgende Art und Weise ausgeben zu lassen:
 

• Standard: Statische Darstellung von Platonischen Körpern im Raumkoordinatensystem (voreingestellt)

• Man.: Manuelle Drehung und Verschiebung von Platonischen Körpern im Raumkoordinatensystem, durch die Bedienung von Rollbalken

• Autosim.: Drehung und Verschiebung von Platonischen Körpern im Raumkoordinatensystem, durch die Ausführung einer Autosimulation

Nach Aktivierung der Kontrollschalter Man. bzw. Autosim. werden Rollbalken mit nachfolgend aufgeführten Bezeichnungen zur Verfügung gestellt, bei deren Bedienung Folgendes durchgeführt wird:
 

• α: Drehung des Platonischen Körpers, um den eingestellten Winkel, um die x-Achse

• β: Drehung des Platonischen Körpers, um den eingestellten Winkel, um die y-Achse

• γ: Drehung des Platonischen Körpers, um den eingestellten Winkel, um die z-Achse

• x: Verschiebung des Platonischen Körpers, um den eingestellten Wert, entlang der x-Achse

• y: Verschiebung des Platonischen Körpers, um den eingestellten Wert, entlang der y-Achse

• z: Verschiebung des Platonischen Körpers, um den eingestellten Wert, entlang der z-Achse

Bzgl. der Funktionalität von Schaltflächen gilt es Folgendes zu berücksichtigen:

 

Schaltfläche Start Sim.:

 

Nach einer Bedienung der Schaltfläche Start Sim. werden die Farben der Polyederflächen vom Programm mit Hilfe eines Zufallsgenerators erzeugt, ansonsten verwendet es die durch Konfiguration voreingestellten Flächenfüllfarben.

 

Schaltfläche Start Rot.:

 

Wurde der Kontrollschalter Autosim. aktiviert, so führt das Programm nach einer Bedienung der Schaltfläche Start Rot. eine Autosimulation durch und bewegt den entsprechenden Polyeder entlang der gewählten Achse(n), bzw. dreht ihn um diese. Alle gewählten Bewegungen werden gleichzeitig und gemeinsam ausgeführt. Für die Auswahl der auszuführenden Bewegungen wird ein Bedienformular zur Verfügung gestellt. Auf diesem wählen Sie, durch die Aktivierung der entsprechenden Kontrollkästchen, die Art der durchzuführenden Simulationen. Mit Hilfe des Rollbalkens Rotationsgeschwindigkeit legen Sie die bei Durchführung der Simulation zu verwendende Rotationsgeschwindigkeit fest. Bedienen Sie hierauf die Schaltfläche Ok, so wird die Simulation ausgeführt. Beenden können Sie diese wieder, wenn Sie die Schaltfläche Stop Rot. bedienen.

 

Rollbalken Bereich:

 

Durch die Positionierung des Rollbalkens im Formularbereich Bereich-Auswahl legen Sie den zur grafischen Ausgabe zu verwendenden Darstellungsbereich fest.

 

Schaltfläche F:

 

Flächenfüllfarben können Sie festlegen, indem Sie die Schaltfläche F bedienen. Aktivieren Sie hierauf den entsprechenden Kontrollschalter zur Auswahl des Vielecks, dem die Farbwerte zugewiesen werden sollen und bewegen Sie die drei zur Verfügung stehenden Schieberegler zur Einstellung der RGB-Werte (Rot, Grün, Blau) bis die entsprechende Füllfarbe im gewünschten Farbton angezeigt wird. Bedienen Sie hierauf die Schaltfläche Ok. Sollen diese Farbeinstellungen sitzungsübergreifend gespeichert werden, so aktivieren Sie zuvor das Kontrollkästchen Speichern. Diese Farbeinstellungen werden nur verwendet, wenn keine Farbsimulation aktiviert wurde.

 

Schaltfläche B:

 

Nach der Ausführung eines Klicks auf die Schaltfläche B kann durch die Aktivierung des Kontrollschalters Solide oder Transparent festgelegt werden, ob die Füllung der Polyederflächen solide oder transparent erfolgen werden soll.

 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen oder deren Frageworte die Wörter Welche?, Welcher?, Welches? bzw. Wodurch? sind, beantwortet werden und zugrunde liegende Sachverhalte können einfach erklärt werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Weitere Videos zum Fachthema Platonische Körper finden Sie auf Youtube unter den folgenden Adressen:

Video 1 - Platonische Körper
Video 2 - Platonische Körper
Video 3 - Platonische Körper
Video 4 - Platonische Körper

Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.

 

 

Archimedische Körper

Spezielle Polyeder

 

Nach einer Aktivierung des Kontrollschalters Tetraeder (Dreiseitige Pyramide), der Eingabe des Zahlenwerts 5 in das Feld Kantenlänge, gibt das Programm nach einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse für das Tetraeder mit der Kantenlänge 5 aus:

Kantenlänge: 5

 

Volumen V: 14,731 VE

Oberfläche O: 43,301 FE

 

Inkugelradius r_i= 1,021

Kantenkugelradius r_k= 2,85

Umkugelradius r_u= 3,061

 

Anzahl der Ecken: 4

Anzahl der Kanten: 6

Anzahl der Flächen: 4

 

Kanten pro Fläche: 3

Kanten pro Ecke: 3

 

Winkel zwischen zwei Flächen: γ = 70° 32'
 

 

Grafische Darstellung - Beispiel 6 - Hexaeder und Ikosaeder


Grafische Darstellung - Beispiel 7 - Hexaeder


Grafische Darstellung - Beispiel 8 - Ikosaeder


Grafische Darstellung - Beispiel 9 - Ikosaeder, Hexaeder und Dodekaeder


Grafische Darstellung - Beispiel 10 - Tetraeder


Grafische Darstellung - Beispiel 11 - Dodekaeder


Grafische Darstellung - Beispiel 12 - Dodekaeder


Grafische Darstellung - Beispiel 13 - Dodekaeder


Grafische Darstellung - Beispiel 14 - Tetraeder


Grafische Darstellung - Beispiel 15 - Ikosaeder


Grafische Darstellung - Beispiel 16 - Dodekaeder


Grafische Darstellung - Beispiel 17 - Dodekaeder

     
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Platonische Körper
Wikipedia - Tetraeder
Wikipedia - Würfel
Wikipedia - Oktaeder
Wikipedia - Dodekaeder
Wikipedia - Ikosaeder
 

 
Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
 

 

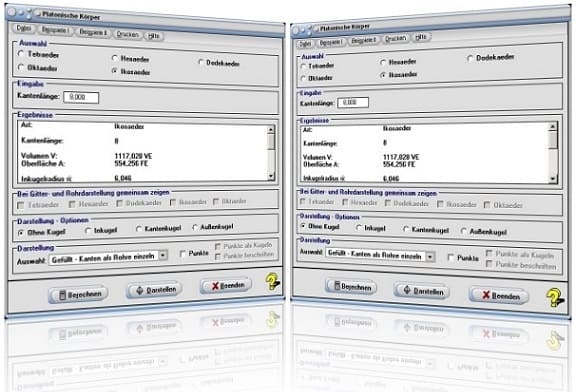
Startfenster des Unterprogramms Platonische Körper
 

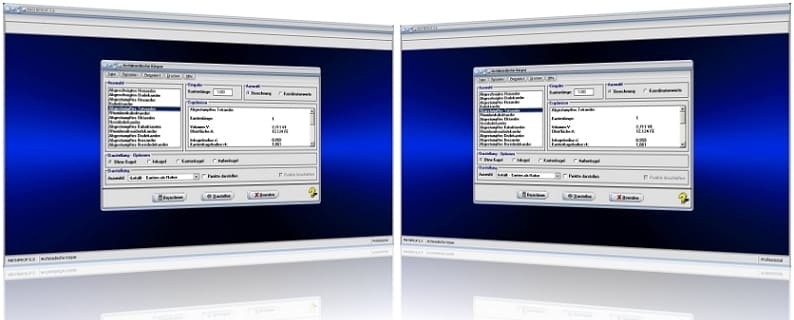
MathProf 5.0 - Startfenster des Unterprogramms Archimedische Körper

---

MathProf 5.0 - Grafikfenster des Unterprogramms Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---