MathProf - Matrizen - Determinanten - Eigenvektoren - Eigenwerte

Fachthemen: Matrizen, Determinanten, Eigenwerte und Eigenvektoren
MathProf - Lineare Algebra - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.
Ein Programm, welches als unter anderem als Begleiter beim Maschinenbau-Studium oder Elektrotechnik-Studium zur Lösung anspruchsvoller Aufgaben sowie zur Erlangung tiefergreifenden Fachwissens der Mathematik eingesetzt werden kann.

Online-Hilfe
für das Modul zur Durchführung verschiedener Matrixoperationen mit quadratischen Matrizen.
Durch den in diesem Unterprogramm integrierten Matrizenrechner erfolgt unter anderem das Berechnen der Eigenwerte einer Matrix sowie derer Eigenvektoren und die Durchführung der Matrizenaddition, der Matrizeninversion, der Matrizenmultiplikation mit zwei Matrizen. Auch das Berechnen der Determinante der entsprechenden Matrix wird vom implementierten Rechner ausgeführt.
Des Weiteren kann die Ausführung der Singulärwertzerlegung (SVD) von Matrizen veranlasst werden. Zudem werden der Rang einer Matrix sowie die Norm einer Matrix (Matrixnorm) ermittelt.
Neben vielen anderen Arten der Matrizenrechnung bestehen in diesem Modul folgende Möglichkeiten Operationen mit Matrizen durchführen zu lassen:
Matrizen addieren, Matrizen subtrahieren, Matrizen multiplizieren, Matrizen dividieren, Matrizen quadrieren, Matrizen potenzieren, Matrizen diagonalisieren, Matrizen transponieren, Matrizen lösen, Matrizen normieren und Matrizen invertieren.
Die Praktizierung der Inversion einer Matrix erfolgt mit Hilfe des Gauß-Jordan-Algorithmus. Zudem kann die Skalarmultiplikation von Matrizen mit reellen Zahlen sowie die Bildung vom Exponential dieser veranlasst werden.
Auch die Berechnung einer Matrix mit komplexen Zahlen wird ermöglicht. Die vom Programm ermittelten numerischen Lösungen werden in einer Tabelle ausgegeben und lassen sich ausdrucken.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte I zu diesem Modul:Matrizen - Matrix - Determinante - Eigenwert - Eigenvektor - Determinanten - Eigenwerte - Eigenvektoren - Matrizenrechnung - Matrizen berechnen - Matrix berechnen - Matrix lösen - Matrizenrechner - Matrizengleichung - Inverse Matrix - Inverse Matrizen - Komplexe Matrizen - Komplexe Matrix - Invertieren - Diagonalisieren - Diagonalisierung - Quadrieren - Addieren - Subtrahieren - Multiplizieren - Dividieren - Transponieren - Potenzieren - Invertierte Matrix - Kehrmatrix - Transponierte Matrix - Normieren - Norm - Matrixnorm - Rang einer Matrix - Charakteristisches Polynom - Dreiecksform - Matrixprodukt - Einführung - Bedeutung - Was bedeutet - Begriff - Begriffe - Welche - Welcher - Welches - Wodurch - Mathe - Mathematik - Dimension - Matrixmultiplikation - Hoch - 2 - 3 - 4 - 5 - Matrix A - Det - Det A - Zahl - Division - Subtraktion - Mal - Durch - Plus - Minus - Orthogonale Matrix - Komplexe Eigenwerte - Komplexe Eigenvektoren - Matrizenmultiplikation - Eigenwertproblem - SVD - Matrix mal Matrix - Singulärwertzerlegung - Einheitsmatrix - Permutationsmatrix - Vertauschungsmatrix - Exponential - Matrixexponential - Lösen - Produktmatrix - Vektoren - Spaltenvektor - Zeilenvektor - Zeilenstufenform - Rechenweg - Algebra - Herleitung - Beweis - Erstellen - Element - Zeile - Spalte - 2x2 - 3x3 - 4x4 - 5x5 - nxn - Invertierbare Matrix - Invertierbare Matrizen - Inverse 2x2 Matrix - Inverse 3x3 Matrix - Diagonalform - Übergangsmatrix - Übungen - Übungsaufgaben - Üben - Aufgaben - Lösungen - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Singularität - Regularität - Übergangsmatrizen - Zwei Matrizen - Antisymmetrische Matrix - Dreiecksmatrix - Diagonale Matrix - Obere Dreiecksmatrix - Untere Dreiecksmatrix - Hauptdiagonale - Nebendiagonale - Laplacescher Entwicklungssatz - Laplace - Unterdeterminante - Algebraisches Komplement - Adjunkte - Matrixexponentialfunktion |
Themen und Stichworte II zu diesem Modul:Symmetrische Matrix - Faktorisieren - Faktorisierung - Operationen - Reguläre Matrix - Singuläre Matrix - Elementarmatrizen - Elementarmatrix - Nullmatrix - Matrizenprodukt - Skalarmultiplikation - Skalar - Eigenwertprobleme - Schiefsymmetrische Matrix - Invertierung - Jacobi-Verfahren - Eigenschaften - Mehrere Matrizen - Erklärung - Einfach erklärt - Beschreibung - Definition - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Bestimmen - Bestimmung - Berechnen - Rechner - Rechnen - Berechnung - Komplex - Plotten - Plotter - Präsentation - Produkt - Vektor - Was ist - Was sind - Lösen - Matrixrechnung - Lösung - Lösen - Bilden - Spalten - Zeilen - Symmetrisch - Asymmetrisch - Matrix umformen - Matrizen umformen - Formel - Schreibweise - Sarrus-Regel - Regel von Sarrus - Vektoren - Addition - Matrizenaddition - Multiplikation - Rechengesetze - Rechenregeln - Gleichheit - Definit - Definitheit - Positiv definit - Semidefinit - Negativ definit - Negativ semidefinit - Indefinit - Stabile Verteilung - Grenzmatrix - Übergangsprozess - Grundoperationen - Zustandsvektor - Minorantenkriterium - Hauptminoren - Minor - Minoren - Diagonalmatrix - Kommutativgesetz - Assoziativgesetz - Gesetze - Regeln |
Matrizen - Determinanten
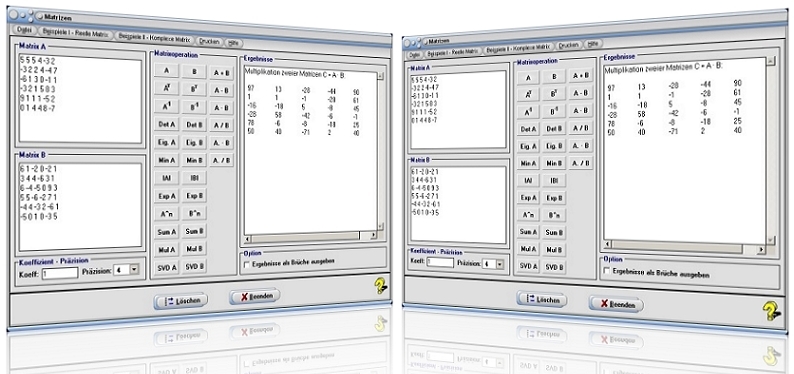
Modul Matrizen
Das Unterprogramm [Algebra] - Matrizen ermöglicht die Durchführung von Matrizenrechnungen (Operationen) mit quadratischen Matrizen.

Der in diesem Modul umgesetzte Matrizenrechner bietet hierbei sowohl die Möglichkeit der Durchführung von Operationen (Berechnungen) mit quadratischen Matrizen reeller Zahlen, wie auch der Ausführung von Operationen (Berechnungen) mit komplexen Zahlen. Eine Übersicht zu den mit diesem Programm durchführbaren Operationen ist im Folgenden zu finden.
1. Matrixoperationen mit Matrizen reeller Zahlen
Grundoperationen mit einer Matrix:
- Transponierung einer Matrix (Transponierte Matrix)
- Invertierung einer Matrix (Inverse Matrix - Matrizeninversion)
- Potenzierung einer Matrix (Potenzierte Matrix)
- Faktorisierung einer Matrix (Faktorisierte Matrix)
- Multiplikation einer Matrix mit einer reellen Zahl (Matrixmultiplikation)
Erweiterte Operationen mit einer Matrix:
- Ermittlung des Werts der Determinante einer Matrix
- Bildung des Exponentials einer Matrix
- Singulärwertzerlegung einer Matrix (SVD)
- Ermittlung der Eigenschaften einer Matrix: Norm einer Matrix, Rang einer Matrix, Dimension einer Matrix, maximales und minimales Element einer Matrix, Summe der Diagonalelemente einer Matrix
- Ermittlung der Eigenwerte und Eigenvektoren einer Matrix
- Ermittlung des minimalen und maximalen Eigenwerts einer Matrix
Operationen mit zwei Matrizen:
- Addieren zweier Matrizen (Matrizenaddition)
- Subtrahieren zweier Matrizen(Matrizensubtraktion)
- Multiplizieren zweier Matrizen (Matrizenprodukt)
- Dividieren zweier Matrizen (Matrizendivision)
- Multiplikation einzelner Elemente zweier Matrizen
- Division einzelner Elemente zweier Matrizen (kein Element der Matrix B darf 0 sein)
2. Matrixoperationen mit Matrizen komplexer Zahlen
Grundoperationen mit einer Matrix komplexer Zahlen:
- Transponierung einer Matrix komplexer Zahlen
- Invertierung einer Matrix komplexer Zahlen
- Potenzierung einer Matrix komplexer Zahlen
- Faktorisierung einer Matrix komplexer Zahlen
- Multiplikation einer Matrix mit einer reellen oder komplexen Zahl (Skalarmultiplikation)
Erweiterte Operationen mit einer Matrix komplexer Zahlen:
- Ermittlung des Werts der Determinante einer Matrix komplexer Zahlen
- Ermittlung der Eigenschaften einer Matrix komplexer Zahlen (Norm, Rang, Dimension, maximales und minimales Element, Summe der Diagonalelemente)
- Ermittlung der Eigenwerte und Eigenvektoren einer Matrix komplexer Zahlen
Operationen mit zwei Matrizen komplexer Zahlen:
- Addition zweier Matrizen komplexer Zahlen
- Subtraktion zweier Matrizen komplexer Zahlen
- Multiplikation zweier Matrizen komplexer Zahlen (Matrixmultiplikation)
- Division zweier Matrizen komplexer Zahlen
- Multiplikation einzelner Elemente zweier Matrizen (Matrizenprodukt)
- Division einzelner Elemente zweier Matrizen (kein Element der Matrix B darf 0 sein)
I - Matrizen
Im folgenden sind Erläuterungen zu wichtigen Grundbegriffen zu diesem Fachthema aufgeführt.
Grundlegendes - Definition - Schreibweise
Definition einer Matrix:
Aus einer Matrix vom Typ (m,n) wird ein aus m·n reellen Zahlen bestehendes rechteckiges Schema verstanden, welches m waagerecht angeordnete Zeilen und n senkrecht angeordnete Spalten besitzt.
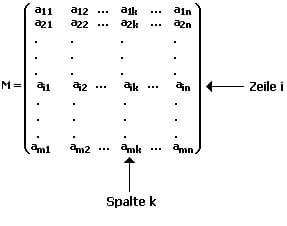
Bezeichnungen:
aik: Matrixelement
i: Zeilenindex (i = 1,2,3 ... m)
j: Spaltenindex (j = 1,2,3 ... n)
Spezielle quadratische Matrizen:
Zeilenmatrix: Eine Zeilenmatrix ist eine Matrix, welche nur eine Zeile besitzt
Spaltenmatrix: Eine Spaltenmatrix ist eine Matrix, welche nur eine Spalte besitzt
Nullmatrix: Eine Nullmatrix ist eine Matrix bei welcher alle Elemente Null sind
Quadratische Matrix: Eine quadratische Matrix ist eine Matrix mit gleich vielen Spalten und Zeilen
Rechteckige Matrix: Eine rechteckige Matrix ist eine Matrix mit n Spalten und m Zeilen, mit m ≠ n
Transponierte Matrix: Eine transponierte Matrix ist eine Matrix bei welcher Zeilen und Spalten miteinander vertauscht sind. Das Durchführen einer Vertauschung dieser Art wird als das Transponieren einer Matrix bezeichnet.
Diagonalmatrix:
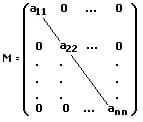
Eine Diagonalmatrix ist eine Matrix, bei welcher alle außerhalb der Diagonale liegenden Elemente verschwinden (gleich Null sind). Eine Matrix dieser Art wird auch als Diagonalform einer Matrix bezeichnet.
Einheitsmatrix:
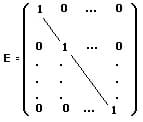
Eine Einheitsmatrix ist eine Matrix, bei welcher alle auf der Diagonale liegenden Elemente den Wert 1 besitzen.
Dreiecksmatrix:
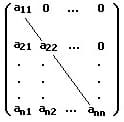
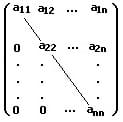
Eine Dreiecksmatrix (oder Dreiecksform einer Matrix) ist eine Matrix, bei welcher alle oberhalb oder unterhalb der Diagonale liegenden Elemente verschwinden (gleich Null sind).
Obere Dreiecksmatrix: Als obere Dreiecksmatrix wird eine Matrix bezeichnet, falls alle Elemente unterhalb der Hauptdiagonale einen Wert von null besitzen.
Untere Dreiecksmatrix: Als untere Dreiecksmatrix wird eine Matrix bezeichnet, falls alle Elemente oberhalb der Hauptdiagonale einen Wert von null besitzen.
Symmetrische Matrix: Eine symmetrische Matrix ist eine Matrix, bei welcher alle Elemente spiegelsymmetrisch zur Hauptdiagonalen angeordnet sind.
Schiefsymmetrische Matrix (antisymmetrische Matrix): Eine schiefsymmetrische Matrix (antisymmetrische Matrix) ist eine Matrix, bei welcher alle Elemente auf der Hauptdiagonalen verschwinden (gleich Null sind).
Reguläre Matrix - Singuläre Matrix (Singularität - Regularität): Eine quadratische, n-reihige Matrix A heisst regulär, wenn ihre Determinante einen von Null verschiedenen Wert besitzt. Ist dies nicht der Fall so heisst sie singulär.
Grenzmatrix: Als Grenzmatrix wird eine Matrix bezeichnet, welche durch eine Multiplikation mit einem beliebigen Zustandsvektor zu einer stabilen Verteilung führt. Sie findet Verwendung bei Austausch- bzw. Übergangsprozessen. Bei einem Übergangsprozess wird aus einer bisherigen Verteilung eine neue berechnet. Jede Spalte einer Grenzmatrix ist in skalarer Form proportional zur stabilen Verteilung. Bei einem derartig ausgeführten Prozess erfolgt die Berechnung einer neuen Verteilung aus der bislang bestehenden.
Zustandsvektor: Mit Hilfe eines Zustandsvektors werden Zustände eines Systems abgebildet. Nach Durchführung einer Multiplikation des Zustandsvektors mit der entsprechenden Übergangsmatrix, wird der Zustand eines Systems beschrieben, welcher nach Ausführung eines weiteren Schritts vorliegt.
Komplexe Matrix: Als komplexe Matrizen werden Matrizen bezeichnet, bei welchen anstelle von reellen Zahlen komplexe Zahlen als Elemente Anwendung finden. Matrizen dieser Art finden z.B. in der Elektrotechnik, insbesondere der Wechselstromtechnik Verwendung. Eine komplexe Matrix besitzt komplexe Eigenwerte und komplexe Eigenvektoren.
Inverse Matrix (Kehrmatrix): Zu jeder regulären Matrix existiert maximal eine inverse Matrix (Kehrmatrix). Reguläre Matrizen lassen sich umkehren. Sie werden als inverse Matrizen bezeichnet. Die zu A inverse Matrix heißt invertierte Matrix und trägt die Bezeichnung A-1. Es gilt:
A·A-1 = A-1·A = E
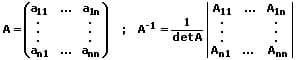
Eine reguläre Matrix ist nur dann umkehrbar (besitzt dann eine inverse Matrix), wenn det A ≠ 0. Das Bilden einer inversen Matrix wird auch Inversion genannt bzw. mit dem Begriff invertieren beschrieben.
Invertierbare Matrix - Invertierbare Matrizen:
Eine Matrix A mit n x n Elementen wird als invertierbar bezeichnet, wenn eine inverse Matrix A-1 mit der gleichen Anzahl an Elementen existiert, so dass gilt: A· A-1 = A-1· A = En. En ist die Einheitsmatrix.
Matrixexponential - Matrixexponentialfunktion: Als Matrixexponential oder Matrixexponentialfunktion wird eine Funktion in Form einer Menge quadratischer Matrizen charakterisiert die gleichbedeutend zur gewöhnlichen Exponentialfunktion definiert ist. Sie besitzt nachfolgend gezeigte Gestalt.

Nachfolgend wird auf die Bedeutung weiterer Fachbegriffe zu diesem Thema eingegangen:
Matrizenrechnung: Als Matrizenrechnung wird das Rechnen mit Matrizen bezeichnet. Matrizenrechnung stellt ein Kerngebiet der linearen Algebra dar und umfasst unter anderem die Addition und Subtraktion von Matrizen sowie die Multiplikation einer Matrix mit einem Skalar. Sie wird unter anderem dafür eingesetzt, lineare Abbildungen darzustellen sowie lineare Gleichungssysteme zu beschreiben und zu lösen.
Zeilenvektor - Spaltenvektor: Matrizen mit nur einer Zeile oder einer Spalte werden Vektoren genannt. Eine einzelne Zeile einer Matrix wird als Zeilenvektor bezeichnet. Eine einzelne Spalte einer Matrix trägt die Bezeichnung Spaltenvektor. Die Summe aller Werte einer Zeile heißt Zeilensumme. Die Summe aller Werte einer Spalte heißt Spaltensumme.
Gleichheit zweier Matrizen: Zwei Matrizen A(i,k) und B(i,k) heißen gleich, wenn sie in all ihren Elementen übereinstimmen.
Matrixmultiplikation - Matrizenmultiplikation: Die Durchführung einer Multiplikation zweier Matrizen wird als Matrixmultiplikation oder Matrizenmultiplikation bezeichnet. Es handelt sich um die multiplikative Verknüpfung von Matrizen.
Elementarmatrix - Elementarmatrizen: Als Elementarmatrix wird eine quadratische Matrix bezeichnet, die sich entweder durch die Änderung eines einzigen Werts oder durch das Vertauschen zweier Zeilen von einer Einheitsmatrix unterscheidet.
Charakteristisches Polynom: Das charakteristische Polynom pA(λ) einer quadratischen Matrix A gibt Auskunft über einige ihrer Eigenschaften. Es wird außerdem zum Berechnen von Eigenwerten und Eigenvektoren verwendet.
Matrixexponential - Matrixexponentialfunktion: Als Matrixexponential oder Matrixexponentialfunktion wird eine Funktion auf der Menge der quadratischen Matrizen bezeichnet. Es handelt sich hierbei um eine mathematische Funktion deren Argument aus einer Matrix besteht.
Orthogonale Matrix: Als orthogonale Matrix wird eine reelle, quadratische Matrix bezeichnet, deren Spalten- und Zeilenvektoren orthogonal hinsichtlich des Skalarprodukts sind.
Matrizengleichung:
Als Matrizengleichungen werden Gleichungen bezeichnet, bei welcher die Elemente einer unbestimmten Matrix zu ermitteln sind.
Produktmatrix:
Das Ergebnis einer durchgeführten Matrizenmultiplikation wird als Matrizenprodukt, Matrixprodukt oder Produktmatrix bezeichnet.
Diagonalisieren (Diagonalisierung) einer Matrix: Unter dem Diagonalisieren einer Matrix wird das Umwandeln einer quadratischen Matrix in eine Diagonalmatrix verstanden.
Rang einer Matrix: Der Rang einer Matrix A vom Typ (m,n) beschreibt die höchste Ordnung r aller von Null verschiedenen Unterdeterminanten von A. Die Schreibweise des Rangs einer Matrix lautet: RG(A) = r
Singulärwertzerlegung: Als Singulärwertzerlegung (abgekürzt SVD) wird die Darstellung einer Matrix in Form eines Produkts dreier besonderer Matrizen bezeichnet. Aus dieser Darstellung können die Singulärwerte einer Matrix abgelesen werden. Diese charakterisieren die Eigenschaften einer Matrix in ähnlicher Form wie die Eigenwerte einer Matrix.
Eigenwerte - Eigenvektoren:
Die Eigenwerte einer Matrix lassen sich als Wurzeln ihres charakteristischen Polynoms interpretieren. Beim Eigenvektor einer Abbildung handelt es sich in der linearen Algebra um einen Vektor, dessen Richtung durch die Abbildung nicht verändert wird. Ein Eigenvektor wird somit lediglich skaliert und nicht verändert. Er darf kein Nullvektor sein. Der hierbei zugrunde liegende Skalierungsfaktor wird als Eigenwert der Abbildung bezeichnet.
Mit Hilfe des charakteristischen Polynoms lassen sich somit die Eigenwerte (und hierauf die Eigenvektoren) einer quadratischen Matrix berechnen. Dies erfolgt, indem dessen Nullstellen bestimmt werden.
Eigenwertproblem: Mit dem Begriff Eigenwertproblem wird die Aufgabe beschrieben, die Eigenwerte und / oder Eigenvektoren einer quadratischen Matrix zu bestimmen.
Jacobi-Verfahren: Das Jacobi-Verfahren (Jacobi Verfahren) wird in diesem Modul zur numerischen Berechnung aller Eigenwerte und Eigenvektoren symmetrischer Matrizen eingesetzt. Es ist ein iteratives Verfahren.
Permutationsmatrix (Vertauschungsmatrix): Bei einer Permutationsmatrix (Vertauschungsmatrix) handelt es sich um eine Matrix, bei der in jeder Spalte und in jeder Zeile exakt ein Eintrag den Wert 1 besitzt und alle anderen Einträge den Wert null besitzen.
Rechengesetze - Rechenregeln - Definitionen
Nachfolgend aufgeführt sind die für Matrizen geltenden Rechengesetze (Rechenregeln).
(A + B ) + C = A + (B + C) (Assoziativgesetz)
A + 0 = A
(A · B ) · C = A · (B · C)
(αA) · B = A · (αB ) = α· (A · B)
C · (A + B ) + C = C · A + C · B
(A + B ) · C = A· C + B · C
(A · B )t = Bt · At
Für quadratische Matrizen gilt zudem:
A · I = I · A = A
Für alle Matrizen gilt:
A · B ≠ B · A
Stochastische Matrix - Übergangsmatrix - Prozessmatrix
Eine Übergangsmatrix wird verwendet, um die Übergangswahrscheinlichkeiten von Markow-Ketten zu formulieren. Übergangsmatrizen sind quadratische Matrizen, bei denen alle Zeilensummen und Spaltensummen den Wert Eins besitzen. Alle ihre Elemente besitzen Werte zwischen Null und Eins. Mit Hilfe derartiger Matrizen lässt sich das Eintreten zukünftiger Zustände im Voraus berechnen. Matrizen dieser Art werden auch mit dem Begriff stochastische Matrix bezeichnet. Prozessmatrizen sind ebenfalls Matrizen die zur Berechnung zukünftiger dynamischer Entwicklungen verwendet werden. Matrizen dieser Art benötigen jedoch keine Zeilen- bzw. Spaltensummen von 1.
II - Determinanten
Definition einer Determinante:
Bei Determinanten handelt es sich um reelle Zahlen, welche quadratischen Matrizen aufgrund bestimmter Rechenvorschriften zugeordnet werden.

aik: Elemente der Determinante (i, k = 1, 2, 3 ... n)
Eine Determinante ist eine Funktion von n x n Veränderlichen, die als quadratisches Schema geschrieben wird. Die in einer Reihe nebeneinander stehenden Elemente bilden ein n-Tupel, welches als Zeile einer Determinante bezeichnet wird. Die aus den in einer Reihe untereinander stehenden Elementen gebildeten m-Tupel sind die Spalten der Determinante.
Dreireihige Determinanten:
Die dreireihige Determinante einer Matrix besitzt den Wert:
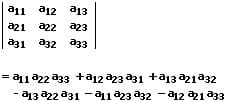
Determinanten dreireihiger Matrizen können nach folgendem Schema, der Regel von Sarrus, errechnet werden:
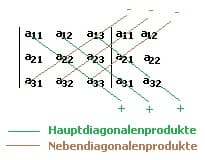
Hierbei werden die beiden ersten Spalten der 3-reihigen Determinante rechts an die Determinante gesetzt. Der Determinantenwert wird ermittelt, indem die drei Hauptdiagonalenprodukte (+) addiert und hiervon die drei Nebendiagonalenprodukte (-) subtrahiert werden. Die Hauptdiagonalen verlaufen von links oben nach rechts unten. Die Nebendiagonalen von links unten nach rechts oben.
Es gilt:
D = a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a11a23a32 - a11a21a33
In Worten: Summe der Produkte der Hauptdiagonalen minus Summe der Produkte der Nebendiagonalen.
Beispiel:
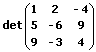
![]()
Eigenschaften einer Determinante:
- Eine Determinante ist in jeder ihrer Zeilen linear
- Beim Vertauschen zweier Zeilen ändert die Determinante ihr Vorzeichen
- Beim Vertauschen der Zeilen mit den Spalten ändert die Determinante ihr Vorzeichen nicht
- Eine Determinante ändert ihren Wert nicht, wenn zu einer Zeile eine Linearkombination anderer Zeilen addiert wird
- Eine Determinante besitzt den Wert Null, wenn eine Zeile lediglich aus Nullen besteht, oder wenn zwei Zeilen identisch sind (wenn die Elemente einer Reihe zu einer parallelen Reihe proportional sind)
Unterdeterminanten (Minoren):
Eine Unterdeterminante entsteht durch das Streichen von k beliebigen Zeilen und k beliebigen Spalten einer n-reihigen Determinante. Hierbei entsteht eine (n-k)-reihige Determinante, welche als (n-k)-te Unterdeterminante der ursprünglichen Determinante bezeichnet wird. Eine Unterdeterminante wird auch als Minor bezeichnet.
Algebraisches Komplement - Adjunkte:
Werden die i-te Zeile und die j-te Spalte einer Determinante gestrichen, so erhält man eine Unterdeterminante (n-1)-ter Ordnung. Wird diese Unterdeterminante mit einem Vorzeichen (-1)j+i versehen, so wird diese Größe das algebraische Komplement oder Adjunkte des Elements aij genannt. Sie wird mit Aij bezeichnet.
Eine Determinante kann nach den Elementen einer beliebigen Zeile entwickelt werden:
D = ai1 · Ai1+ ai2 · Ai2 + ai3 · Ai3 + ... ain · Ain
Laplacescher Entwicklungssatz:
Mit Hilfe des Laplaceschen Entwicklungssatzes lässt sich eine Determinante nach den Elementen einer beliebigen Zeile oder Spalte entwickeln.
Bei der Entwicklung nach den Elementen der i-ten Zeile gilt:

Bei der Entwicklung nach den Elementen der k-ten Spalte gilt:

Aik = (-1)i+k·Dik
Aik: Algebraisches Komplement von aik in D
Dik: (n-1)-reihige Unterdeterminante von D
Regeln zum Rechnen mit Determinanten:
Der Werte einer n-reihigen Determinante ändert sich nicht, wenn eine der nachfolgenden Umformungen mit ihr durchgeführt wird:
1. Besitzen alle Elemente einer Zeile oder Spalte einen gemeinsamen Faktor λ, so darf dieser vor die Deteminante gezogen werden.
2. Wird zu einer Zeile bzw. Spalte einer Determinante ein beliebiges Vielfaches einer anderen Zeile bzw. Spalte addiert, so ändert sich der Wert der Determinante nicht.
3. Zwei Zeilen oder Spalten einer Determinante dürfen vertauscht werden, wenn das Vorzeichen der Determinante geändert wird.
Hinweise zur Definitheit einer Matrix
Definitheit einer Matrix:
Durch die Bestimmung der Definitheit wird ermittelt, welche Vorzeichen eine reelle quadratische Form annehmen kann, die durch eine Matrix erzeugt wurde. Durch die Untersuchung, ob eine Matrix positiv oder negativ definit ist kann geprüft werden, ob entsprechende Bedingungen erfüllt werden. Besitzt eine Matrix weder eine positive noch eine negative Definitheit oder Semidefinitheit, so wird sie als indefinit bezeichnet. Unter anderem erfolgt durch deren Ermittlung bei der Bestimmung lokaler, mehrdimensionaler Extremstellen die Kategorisierung hinsichtlich der Tatsache, ob es sich um Maxima oder Minima handelt. Zur Bestimmung der Definitheit von Matrizen existieren verschiedene Methoden. Die beiden meist angewandten sind die Eigenwertmethode sowie die Bestimmung des Hauptminorantenkriteriums.
Um zu untersuchen, ob eine Matrix positiv oder negativ definit ist, wird folgende Vorgehensweise angewandt:
Ist x ∈ Rn ein n-zeiliger Spaltenvektor und xT der zugehörige transponierte Zeilenvektor, so ist eine symmetrische Matrix A ∈ Rnxn unter Betrachtung der quadratischen Form:
positiv definit, falls xTAx > 0, ∀ x ∈ Rn, x ≠ 0
positiv semidefinit, falls xTAx ≥ 0, ∀ x ∈ Rn, x ≠ 0
negativ definit, falls xTAx < 0, ∀ x ∈ Rn, x ≠ 0
negativ semidefinit, falls xTAx ≤ 0, ∀ x ∈ Rn, x ≠ 0
mit:
x ∈ R: n-zeiliger Spaltenvektor
xT: transponierter Zeilenvektor
Um zu untersuchen, ob eine Matrix A ∈ Rnxn positiv definit, negativ definit, semidefinit oder indefinit ist, wird die Eigenwertmethode verwendet. Für A gilt:
alle λi > 0: positiv definit
alle λi ≥ 0: positiv semidefinit
alle λi < 0: negativ definit
alle λi ≤ 0: negativ semidefinit
Besitzt A sowohl positive, wie auch negative Eigenwerte, so ist die Matrix indefinit.
mit:
λi, i,1 ...,n
Details zur Definitheit sowie deren Bestimmung sind unter Wikipedia - Definitheit zu finden.
III - Programmbedienung
Im Folgenden wird auf die Benutzung dieses Programmmoduls eingegangen.
Bedienschaltflächen
Die Bedienung einer Schaltfläche in diesem Unterprogramm mit nachfolgend aufgeführten Bezeichnungen bewirkt:
| A: | Ausgabe einer Matrix A |
| AT: | Transponierung einer Matrix A |
| A-1: | Bildung der Inverse INV(A) einer Matrix A |
| Det A: | Ermittlung der Determinante einer Matrix A |
| Eig. A: | Ermittlung der Eigenwerte sowie der Eigenvektoren einer Matrix A |
| Min A: | Ermittlung des min. und max. Eigenwerts einer Matrix A, sowie derer zugehöriger Eigenvektoren |
| |A|: | Bestimmung der Norm, des Rangs, der Dimension, sowie Ausgabe des minimalen und maximalen Elements einer Matrix A |
| Exp A: | Bildung des Exponentials Exp(A) einer Matrix A |
| A^n: | Potenzierung einer Matrix A mit dem Wert n, der im Eingabefeld Koeff. festgelegt wurde |
| Sum A: | Bildung der Summe der Diagonalelemente einer Matrix A |
| Mul A: | Multiplikation aller Elemente einer Matrix A mit einem Faktor, der im Eingabefeld Koeff. festgelegt wurde |
| SVD A: | Singulärwertzerlegung der Matrix A(SVD) → A = USV |
| B: | Ausgabe einer Matrix B |
| BT: | Transponierung einer Matrix B |
| B-1: | Bildung der Inverse INV(A) einer Matrix B |
| Det B: | Ermittlung der Determinante einer Matrix B |
| Eig. B: | Ermittlung der Eigenwerte sowie der Eigenvektoren einer Matrix B |
| Min B: | Ermittlung des min. und max. Eigenwerts einer Matrix B, sowie derer zugehöriger Eigenvektoren |
| |B|: | Bestimmung der Norm, des Rangs, der Dimension, sowie Ausgabe des minimalen und maximalen Elements einer Matrix B |
| Exp B: | Bildung des Exponentials Exp(B) einer Matrix B |
| B^n: | Potenzierung einer Matrix B mit dem Wert n, der im Eingabefeld Koeff. festgelegt wurde |
| Sum B: | Bildung der Summe der Diagonalelemente einer Matrix B |
| Mul B: | Multiplikation aller Elemente einer Matrix B mit einem Faktor, der im Eingabefeld Koeff. festgelegt wurde |
| SVD B: | Singulärwertzerlegung der Matrix B(SVD) → B = USV |
| A+B: | Addition einer Matrix A und einer Matrix B → C = A+B |
| A-B: | Subtraktion einer Matrix B von einer Matrix A → C = A-B |
| A·B: | Multiplikation einer Matrix A mit einer Matrix B → C = A·B (Matrizenprodukt) |
| A/B: | Division einer Matrix B durch eine Matrix A → C = A/B |
| A.·B: | Multiplikation der Elemente einer Matrix A mit den Elementen einer Matrix B → C = A.·B |
| A./B: | Division der Elemente einer Matrix B durch die Elemente einer Matrix A → C = A./B |
Berechnung - Matrix-Operationen
Voraussetzungen:
Matrixelemente müssen durch (mindestens ein) Leerzeichen voneinander getrennt werden. Zwischen negativen Vorzeichen (Minuszeichen) und Zahlenwerten darf sich kein Leerzeichen befinden. Die Anzahl der Matrixelemente einer Reihe muss mit der Anzahl der Matrixelemente einer Zeile übereinstimmen (n x n - Matrix). Das Programm erkennt (bei korrekter Zahlenwerteingabe) die Dimension der Matrix automatisch, es ist hierfür nichts einzustellen. Zeilen sollten lückenlos von oben nach unten beschrieben werden. Als Dezimalseparatoren sind sowohl Punkt als auch Komma zugelassen. Die Anzahl der Zeilen bzw. Spalten darf die Zahl 50 nicht überschreiten (max. 50 x 50 - Matrix).
Bei Berechnungen mit komplexen Zahlen gilt:
Zwischen dem Realteil und dem Imaginärteil einer komplexen Zahl darf sich kein Leerzeichen befinden (sondern lediglich die Zeichen + oder -). Das Programm erkennt automatisch, ob es Berechnungen mit komplexen Zahlen durchzuführen hat, oder nicht. Es ist hierfür nichts einzustellen. Besitzt eine komplexe Zahl keinen Realteil, so kann diese Zahl auf eine der folgenden Arten definiert werden: 0+3i oder 3i. Besitzt sie keinen Imaginärteil, so kann sie wie folgt definiert werden: 2+0i oder 2.
Sind o.a. Bedingungen erfüllt, so führen Sie Folgendes aus, um Berechnungen mit Matrizen durchführen zu lassen:
- Zur Ausführung von Operationen mit nur einer Matrix, definieren Sie deren Koeffizienten im Eingabebereich Matrix A bzw. Matrix B.
- Vor Durchführung der Potenzierung, oder der Multiplikation aller Elemente einer Matrix legen Sie im Eingabefeld Koeff. den Wert des Koeffizienten für die entsprechende Operation fest (auch die Eingabe komplexer Zahlenwerte ist möglich, z.B. 3+2i).
- Die Anzahl zu verwendender Dezimalstellen bei der Ausgabe von Ergebnissen bestimmen Sie durch die Wahl des gewünschten Werts aus der Auswahlliste Präzision (voreingestellt: 4).
- Bedienen Sie hierauf die entsprechende Schaltfläche zur Durchführung einer Operation, so gibt das Programm die Ergebnisse dieser im rechtsseitig angeordneten Ausgabefeld aus (sind nicht alle Ergebnisse zu sehen, so bedienen Sie den horizontalen bzw. vertikalen Rollbalken des Ausgabefelds).
- Sind die Ergebnisse im Ausgabefeld zu löschen, so klicken Sie auf die Schaltfläche Löschen.
- Um die Eingaben der Werte für Matrix A oder Matrix B zu löschen, klicken Sie in die linke obere Ecke des entsprechenden Eingabefelds, markieren dieses bei Gedrückthalten der linken Maustaste und einer Bewegung des Cursors von oben nach unten und bedienen hierauf die Taste Entf. Alternativ hierzu kann auch der Menübefehl Urzustand herstellen verwendet werden.
-
Möchten Sie mit den Ergebniswerten einer ermittelten Matrix weitere Operationen durchführen, so markieren Sie diese im Ausgabefeld durch ein Gedrückthalten und eine anschließende Bewegung der linken Maustaste.
Verwenden Sie hierauf die Tastenkombination Strg-C (Kopieren in Zwischenablage) und löschen Sie die Eingaben im entsprechenden links angeordneten Eingabefeld für Matrix A oder Matrix B. Klicken Sie in die linke obere Ecke des entsprechenden Eingabefelds und benutzen Sie die Tastenkombination Strg-V (Einfügen aus Zwischenablage).
Sofern die o.a. Voraussetzungen erfüllt sind, können hierauf weitere Operationen mit den Werten der zuletzt ermittelten Matrix durchgeführt werden. Das Programm formatiert kopierte Matrizen hierbei automatisch bei Durchführung einer nächsten Operation - es sind somit keine Veränderungen (Entfernung von Leerzeichen etc.) notwendig.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Beispiele
Beispiel 1 - Reelle Zahlenwerte:
Gegeben sei Matrix A:
| 8 | 1 | -7 | -2 |
| 3 | -2 | 8 | 0 |
| -5 | 1 | 3 | -4 |
| 6 | 0 | -1 | 3 |
sowie Matrix B:
| -4 | 1 | -2 | 6 |
| 6 | -1 | 4 | -6 |
| 3 | -4 | -3 | -3 |
| -2 | 5 | -8 | -6 |
Es gilt, alle nachfolgend aufgeführten Operationen mit diesen Matrizen durchführen zu lassen.
-
Transponierung einer Matrix
-
Invertierung einer Matrix
-
Ermittlung der Determinante einer Matrix
-
Ermittlung der Eigenwerte und Eigenvektoren einer Matrix
-
Ermittlung des minimalen und maximalen Eigenwerts einer Matrix
-
Ermittlung der Norm, des Rangs, der Dimension, des minimalen und maximalen Elements einer Matrix
-
Bildung des Exponentials einer Matrix
-
Potenzierung einer Matrix
-
Ermittlung der Summe der Diagonalelemente einer Matrix
-
Multiplikation einer Matrix mit einer reellen Zahl
-
Singulärwertzerlegung einer Matrix (SVD)
-
Multiplikation einzelner Elemente zweier Matrizen
-
Division einzelner Elemente zweier Matrizen
-
Addition zweier Matrizen
-
Subtraktion zweier Matrizen
-
Multiplikation zweier Matrizen (Matrizenprodukt)
-
Division zweier Matrizen
Legen Sie hierfür alle Zahlenwerte der Koeffizienten für Matrix A und Matrix B in den dafür vorgesehenen Bereichen fest.
Transponierung einer Matrix
Wird ein Klick auf Schaltfläche AT ausgeführt, so wird für die zu A transponierte Matrix AT ausgegeben:
Transponierte Matrix AT:
| 8 | 3 | -5 | -6 |
| 1 | -2 | 1 | 0 |
| -7 | 8 | 3 | -1 |
| -2 | 0 | -4 | 3 |
Invertierung einer Matrix
Ein Klick auf die Schaltfläche A-1 bewirkt die Ausgabe der Inverse Inv(A) der Matrix A:
Inverse der Matrix A - Inv(A):
| -0,5152 | -0,4242 | -0,3333 | -0,7879 |
| -4,9545 | -4,2273 | -2,5 | -6,6364 |
| -1,0455 | -0,7727 | -0,5 | -1,3636 |
| -1,3788 | -1,1061 | -0,8333 | -1,697 |
Determinante einer Matrix
Nach einer Bedienung der Schaltfläche Det A wird für die Determinante Det(A) der Matrix A ausgegeben:
Determinante der Matrix A: Det(A) = 66
Eigenwerte und Eigenvektoren einer Matrix
Bei einer Bedienung der Schaltfläche Eig. A wird für die Eigenwerte und Eigenvektoren der Matrix A ausgegeben:
Eigenwerte der Matrix A:
| 11,28 |
| -5,9862 |
| 6,8489 |
| -0,1427 |
Eigenvektoren der Matrix A:
| -0,809 | 1 | -0,7045 | -0,6836 |
| 0,3393 | 1 | 0,3794 | 0,6703 |
| -0,0283 | 0,1508 | 1 | -0,7765 |
| 1 | 0,1657 | -0,4041 | -0,5247 |
Minimaler und maximaler Eigenwert einer Matrix
Nach Ausführung eines Klicks auf die Schaltfläche Min A ermittelt das Programm für Matrix A:
Maximaler Eigenwert der Matrix A: Max. Eig(A) = 11,28
Zugehörige Eigenvektoren:
| 1 |
| 0,0689 |
| -0,2607 |
| -0,6932 |
Minimaler Eigenwert der Matrix A: Min. Eig(A) = -0,1427
Zugehörige Eigenvektoren:
| 0,1075 |
| 1 |
| 0,1918 |
| 0,2663 |
Norm, Rang, Dimension, minimales und maximales Element einer Matrix
Wird die Schaltfläche |A| bedient, so gibt das Programm für Matrix A aus:
Norm der Matrix A: Norm(A) = 17,08801
Rang der Matrix A: Rang(A) = 4
Dimension der Matrix A: Dim(A) = 4·4
Minimales/maximales Element der Matrix A:
Min(A) = -7
Max(A) = 8
Potenzierung einer Matrix
Wird der Wert 2 in das Feld Koeff. eingegeben und wird ein Klick auf die Schaltfläche A^n ausgeführt, so ermittelt das Programm für die mit 2 potenzierte Matrix A2:
Potenzierte Matrix A^(2):
| 114 | -1 | -67 | 6 |
| -22 | 15 | -13 | -38 |
| -28 | -4 | 56 | -14 |
| -61 | -7 | 36 | 25 |
Summe der Diagonalelemente einer Matrix
Für die Summe der Diagonalelemente der Matrix A gibt das Programm nach einem Klick auf die Schaltfläche Sum A aus:
Summe der Diagonalelemente der Matrix A: Sum(A) = 12
Multiplikation einer Matrix mit einer reellen Zahl
Nach der Eingabe des Werts 3 in das Feld Koeff. und einem Klick auf die Schaltfläche Mul A multipliziert das Programm die Elemente der Matrix mit dem festgelegten Faktor 3 und gibt aus:
Mit Faktor multiplizierte Matrix A·3:
| 24 | 3 | -21 | -6 |
| 9 | -6 | 24 | 0 |
| -15 | 3 | 9 | -12 |
| -18 | 0 | -3 | 9 |
Singulärwertzerlegung einer Matrix (SVD)
Wird ein Klick auf die Schaltfläche SVD A ausgeführt, gibt das Programm für die Matrix A aus:
Singulärwertzerlegung der Matrix A (SVD): A = USV
Matrix U:
| -0,8243 | 0,0186 | 0,2318 | -0,5162 |
| 0,2426 | 0,8482 | -0,1769 | -0,4363 |
| 0,4087 | -0,0711 | 0,8707 | -0,2641 |
| 0,3077 | -0,5245 | -0,396 | -0,688 |
Matrix S:
| 13,0894 | 0 | 0 | 0 |
| 0 | 9,5784 | 0 | 0 |
| 0 | 0 | 5,377 | 0 |
| 0 | 0 | 0 | 0,0979 |
Matrix V:
| -0,7453 | 0,6469 | -0,1217 | 0,1058 |
| -0,0688 | -0,1826 | 0,2709 | 0,9426 |
| 0,6593 | 0,7273 | -0,0056 | 0,1906 |
| 0,0716 | -0,1385 | -0,9549 | 0,2528 |
Multiplikation einzelner Elemente zweier Matrizen
Nach einem Klick auf die Schaltfläche A. · B führt das Programm eine Multiplikation aller einzelner Elemente der Matrix A mit den entsprechenden Elementen der Matrix B durch und gibt für Matrix C aus:
Multipl. der Elemente zweier Matrizen C = A. · B
| -32 | 1 | 14 | -12 |
| 18 | 2 | 32 | 0 |
| -15 | -4 | -9 | 12 |
| 12 | 0 | 8 | -18 |
Division einzelner Elemente zweier Matrizen
Um eine Division aller einzelner Elemente der Matrix A durch die entsprechenden Elemente der Matrix B durchführen zu lassen wird ein Klick auf die Schaltfläche A. / B ausgeführt und das Programm gibt für Matrix C aus:
Division der Elemente zweier Matrizen C = A. / B
| -2 | 1 | 3,5 | -0,3333 |
| 0,5 | 2 | 2 | 0 |
| -1,6667 | -0,25 | -1 | 1,3333 |
| 3 | 0 | 0,125 | -0,5 |
Addition zweier Matrizen
Nach einem Klick auf die Schaltfläche A + B sowie der Durchführung einer Addition der Matrizen A und B gibt das Programm für Matrix C aus:
Additition zweier Matrizen C = A + B:
| 4 | 2 | -9 | 4 |
| 9 | -3 | 12 | -6 |
| -2 | -3 | 0 | -7 |
| -8 | 5 | -9 | -3 |
Subtraktion zweier Matrizen
Die Subtraktion der Matrix B von Matrix A, wird nach einem Klick auf die Schaltfläche A - B durchgeführt. Für die resultierende Matrix C gibt das Programm aus:
Subtraktion zweier Matrizen C = A - B:
| 12 | 0 | -5 | -8 |
| -3 | -1 | 4 | 6 |
| -8 | 5 | 6 | -1 |
| -4 | -5 | 7 | 9 |
Multiplikation zweier Matrizen (Matrizenprodukt)
Bei Durchführung einer Multiplikation der Matrizen A und B gibt das Programm einem Klick auf die Schaltfläche A · B für Matrix C aus:
Multiplikation zweier Matrizen C = A · B:
| -43 | 25 | 25 | 75 |
| 0 | -27 | -38 | 6 |
| 43 | -38 | 37 | -21 |
| 15 | 13 | -9 | -51 |
Division zweier Matrizen
Nach einem Klick auf die Schaltfläche A / B, sowie der Durchführung einer Division der Matrizen B durch A gibt das Programm für Matrix C aus:
Division zweier Matrizen C = A/B:
| 8,1667 | 6,2917 | 1,8333 | 1,2917 |
| -1 | -0,125 | -0,5 | -0,625 |
| -6,7121 | -4,7803 | -1,4242 | -0,553 |
| -3 | -2,875 | -0,5 | -0,375 |
Beispiel 2 - Komplexe Zahlenwerte:
Gegeben sei Matrix A:
| -5+i | i | -7+7i | 2-6i |
| -5i | -2+6i | 8-i | 0 |
| -2+i | 1-i | 3+6i | 0 |
| i | 3+i | 3-5i | -2+2 |
sowie Matrix B:
| 2+i | 1-i | -3+3i | 2 |
| -6i | -1-i | 4+i | -5+5i |
| -4i | -6i | 5 | -3 |
| 8-2i | 5+i | -7+7i | 6-6i |
Es gilt, alle nachfolgend aufgeführten Operationen mit diesen Matrizen durchführen zu lassen.
-
Transponierung einer komplexen Matrix
-
Invertierung einer komplexen Matrix
-
Ermittlung der Determinante einer komplexen Matrix
-
Ermittlung der Eigenwerte und Eigenvektoren einer komplexen Matrix
-
Ermittlung des minimalen und maximalen Eigenwerts einer komplexen Matrix
-
Multiplikation einer komplexen Matrix mit einer reellen Zahl
-
Ermittlung der Norm, des Rangs, der Dimension, des minimalen und maximalen Elements einer komplexen Matrix
-
Ermittlung der Summe der Diagonalelemente einer komplexen Matrix
-
Multiplikation einzelner Elemente zweier komplexen Matrizen mit komplexen Zahlen
-
Division einzelner Elemente zweier komplexer Matrizen mit komplexen Zahlen
-
Addition zweier komplexer Matrizen mit komplexen Zahlen
-
Subtraktion zweier komplexer Matrizen mit komplexen Zahlen
-
Multiplikation zweier komplexer Matrizen mit komplexen Zahlen (Matrizenprodukt)
-
Division zweier komplexer Matrizen mit komplexen Zahlen
Legen Sie hierfür alle komplexen Zahlenwerte der Koeffizienten für Matrix A und Matrix B in den dafür vorgesehenen Bereichen fest.
Transponierung einer Matrix mit komplexen Zahlen
Wird ein Klick auf Schaltfläche AT ausgeführt, so wird für die zu A transponierte Matrix AT ausgegeben:
Transponierte Matrix AT:
| -5+ | -5i | -2+i | i |
| i | -2+6i | 1-i | 3+i |
| -7+7i | 8-i | 3+6i | 3-5i |
| 2-6i | 0 | 0 | -2+2i |
Invertierung einer Matrix mit komplexen Zahlen
Ein Klick auf die Schaltfläche A-1 bewirkt die Ausgabe der Inverse Inv(A) der Matrix A:
| 0,266-0,36i | 0,45+0,123i | -0,144-0,078i | 0,173-0,986i |
| 0,186-0,409i | 0,44-0,101i | -0,003-0,019i | -0,037-1,005i |
| -0,026-0,079i | 0,09-0,067i | 0,044-0,087i | -0,13-0,132i |
| 0,435-0,006i | 0,33+0,295i | 0,118-0,226i | 0,614-0,698i |
Wird der Wert 3 in das Feld Koeff. eingegeben und wird ein Klick auf die Schaltfläche A^n ausgeführt, so ermittelt das Programm für die mit 3 potenzierte Matrix A3:
| -75+274i | -104+213i | 516-53i | -194-398i |
| -540-340i | 298-19i | -1403+421i | 390-70i |
| 112+14i | -72+109i | 309+123i | -174-18i |
| -69+194i | 85-217i | -47+558i | -52 |
Determinante einer Matrix mit komplexen Zahlen
Nach einer Bedienung der Schaltfläche Det A wird für die Determinante Det(A) der Matrix A ausgegeben:
Determinante der Matrix A: Det(A) = 320-48i
Eigenwerte und Eigenvektoren einer Matrix mit komplexen Zahlen
Bei einer Bedienung der Schaltfläche Eig. A wird für die Eigenwerte und Eigenvektoren der Matrix A ausgegeben:
Eigenwerte der Matrix A:
| 0,4559+0,3403i |
| 5,7661+3,7198i |
| 8,0538+1,8026i |
| 4,1682+9,1373i |
Eigenvektoren der Matrix A:
| 0,91+0,26i | 1 | 0,16-0,12i | 0,59+0,71i |
| -0,26+0,61i | 1 | 0,64-0,37i | 0,205-0,5i |
| 1 | 0,45+0,68i | 0,03-0,12i | -0,041-0,49i |
| -0,44+0,02i | 1 | -0,29+0,08i | 0,194-0,41i |
Multiplikation einer Matrix mit komplexen Zahlen mit einer reellen Zahl
Nach der Eingabe des Werts 2 in das Feld Koeff. und einem Klick auf die Schaltfläche Mul A multipliziert das Programm die Elemente der Matrix mit dem festgelegten reellen Faktor 2 und gibt aus:
Mit Faktor multiplizierte Matrix A·2:
| -10+2i | 2i | -14+14i | 4-12i |
| -10i | -4+12i | 16-2i | 0 |
| -4+2i | 2-2i | 6+12i | 0 |
| 2i | 6+2i | 6-10i | -4+4i |
Norm, Rang, Dimension, minimales, maximales Element und Summe der
Diagonalelemente einer Matrix mit komplexen Zahlen
Wird die Schaltfläche |A| bedient, so gibt das Programm für Matrix A aus:
Norm der Matrix A: Norm(A) = 13,49074
Rang der Matrix A: Rang(A) = 4
Dimension der Matrix A: Dim(A) = 4·4
Minimales/maximales Element der Matrix A:
Min(A) = -7+7i
Max(A) = 8-i
Summe der Diagonalelemente der Matrix A: Sum(A) = -6+15i
Multiplikation einzelner Elemente zweier Matrizen mit komplexen Zahlen
Nach einem Klick auf die Schaltfläche A. · B führt das Programm eine Multiplikation aller einzelner Elemente der Matrix A mit den entsprechenden Elementen der Matrix B durch und gibt für Matrix C aus:
Multipl. der Elemente zweier Matrizen C = A. · B
| -11-3i | 1+i | -42i | 4-12i |
| -30 | 8-4i | 0 | 0 |
| 4+8i | -6-6i | 18-9i | 0 |
| 2+8i | 14+8i | 14+56i | 24i |
Division einzelner Elemente zweier Matrizen mit komplexen Zahlen
Um eine Division aller einzelner Elemente der Matrix A durch die entsprechenden Elemente der Matrix B durchzuführen wird ein Klick auf die Schaltfläche A. / B ausgeführt und das Programm gibt für Matrix C aus:
Division der Elemente zweier Matrizen C = A. / B
| -1,8+1,4i | -0,5+0,5i | 2,3333 | 1-3i |
| 0,8333 | -2-4i | 1,824-0,706i | 0 |
| -0,25-0,5i | 0,1667+0,167i | -2+1i | 0 |
| -0,0294+0,117i | 0,6154+0,077i | -0,571+0,143i | -0,333 |
Addition zweier Matrizen mit komplexen Zahlen
Nach einem Klick auf die Schaltfläche A + B sowie der Durchführung einer Addition der Matrizen A und B gibt das Programm für Matrix C aus:
Additition zweier Matrizen C = A + B:
| -3+2i | 1 | -10+10i | 4-6i |
| -11i | -3+5i | 12 | -5+5i |
| -2-3i | 1-7i | 3+3i | 5 |
| 8-i | 8+2i | -4+2i | 4-4i |
Subtraktion zweier Matrizen mit komplexen Zahlen
Die Subtraktion der Matrix B von Matrix A wird nach einem Klick auf die Schaltfläche A - B durchgeführt. Für die resultierende Matrix C gibt das Programm aus:
Subtraktion zweier Matrizen C = A - B:
| -7 | -1+2i | -4+4i | -6i |
| i | -1+7i | 4-2i | 5-5i |
| -2+5i | 1+5i | 3+9i | -5 |
| -8+3i | -2 | 10-12i | -8+8i |
Multiplikation zweier Matrizen mit komplexen Zahlen (Matrizenprodukt)
Bei Durchführung einer Multiplikation der Matrizen A und B, gibt das Programm einem Klick auf die Schaltfläche A · B für Matrix C aus:
Multiplikation zweier Matrizen C = A · B:
| 27-27i | 55+19i | 60+63i | -74-16i |
| 37-30i | -3-57i | -2+13i | 20-55i |
| 13-18i | 33-15i | 26-21i | 11+42i |
| -27-8i | -43-13i | -7-33i | -5+11i |
Division zweier Matrizen mit komplexen Zahlen
Nach einem Klick auf die Schaltfläche A / B sowie der Durchführung einer Division der Matrizen B durch A gibt das Programm für die resultierende Matrix C aus:
Division zweier Matrizen C = A/B:
| 1,344+1,178i | -0,31-0,753i | -0,632-0,755i | 0,329-0,803i |
| -2,548-1,84i | 0,408-0,528i | -0,399+0,078i | 0,656+0,425i |
| 1,377-0,62i | -0,335-0,492i | -0,457+0,253i | -0,315-0,452i |
| -1,123+0,53i | -0,254+0,175i | 0,085+0,577i | -0,065-0,031i |

Beispiel 1

Beispiel 2

Beispiel 3

Beispiel 4

Beispiel 5

Beispiel 6

Beispiel 7

Beispiel 8
Dieses Modul eignet sich neben vielem anderem auch zum Üben bereits erlernter Kenntnisse zu diesem Fachthema. Übungsaufgaben lassen sich durch benutzerdefinierte Festlegungen und Eingaben erstellen und unmittelbar hierauf numerisch bzw. grafisch auswerten. Übungen zu diesem Themengebiet können somit auf einfache Weise praktiziert werden, oder dazu genutzt werden, die Lösungen gestellter Aufgaben zu überprüfen und zu analysieren.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Matrizen sowie unter Wikipedia - Eigenwertproblem zu finden.
Cramersche Regel - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
MathProf 5.0 - Unterprogramm Cramersche Regel

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















