MathProf - Jahreszins - Prozente - Promille - Prozentrechnung - Grundwert

Modul Jahreszinsrechnung

---

 
Das Unterprogramm [Sonstiges] - Jahreszinsrechnung ermöglicht die Berechnung von Jahreszinsen bei Veränderung des Kontostands.

 

 
 

Hierbei wird die Durchführung der Berechnung der Jahreszinsen gemäß einem frei definierbaren Sparplan nach folgenden Methoden ermöglicht:
 

• Einzahlung: Zahlenwerteingaben (Betragsangaben) werden als Einzahlungen am entsprechenden Tag interpretiert
   

• Kontostand: Zahlenwerteingaben (Betragsangaben) werden als Kontostände am entsprechenden Datum interpretiert

In beiden Fällen wird von einem Kapital zu Jahresbeginn von 0 € ausgegangen. Zudem wird angenommen, dass ab dem zuletzt eingegebenen Datum bis zum Jahresende keine Kontostandsveränderungen mehr eintreten. Bei der hierzulande üblichen Zinsrechnung besitzt ein Monat stets 30 Tage (inkl. Februar). Ein Jahr verfügt über 12 Mionate und ein Zinsjahr besitzt einen Zeitraum von 360 Tagen.

Sparplan: Unter einem Sparplan wird eine einfache Geldanlageform verstanden, mit Hilfe derer regelmäßig und langfristig Vermögen aufgebaut wird.
  
Zinszahlung: Eine Zinszahlung ist eine für Zinsen aufgewendete Zahlung.

Zinstag: Bei Zinstagen handelt es sich bei der Zinsrechnung um einen Kalendertag, an dem Zinsen für Liquidationen oder Verbindlichkeiten berechnet werden.

Jahreszinsen: Von Jahreszins wird gesprochen, wenn der Zins einmalig pro Jahr gesculdet wird. Er wird durch Kürzelbezeichnung p.a. (par annum - proo Jahr) gekennzeichnet.

Zinsjahr: Ein Zinsjahr umfasst 360 Tage. Für jeden Monat werden 30 Zinstage zugrundegelegt.
 

 

 
 

Gehen Sie folgendermaßen vor, um Jahreszinsberechnungen durchführen zu lassen:
 

1. Aktivieren Sie den entsprechenden Kontrollschalter Einzahlung bzw. Kontostand um festzulegen ob Zahlenwerte als Einzahlung, oder als Kontostand zu interpretieren sind.
    

2. Legen Sie durch die Eingabe eines entsprechenden Werts in das Feld Zinssatz den (stetigen) Jahreszinssatz (in %) fest.
    

3. Wählen Sie durch die Aktivierung des Kontrollschalters 360 Tage bzw. 365 Tage, ob Berechnungen mit der Methode 360 Tage oder mit der Methode 365 Tage durchgeführt werden sollen.
    

4. Legen Sie durch die Eingabe von Datumsangaben die Buchungstage fest und weisen Sie diesen die entsprechenden Kontostände, bzw. Einzahlungen zu.
    

5. Sollen die Berechnungen für ein Schaltjahr durchgeführt werden, so aktivieren Sie das Kontrollkästchen Schaltjahr.
    

6. Bedienen Sie die Schaltfläche Berechnen, so gibt das Programm die Ergebnisse auf einem Unterformular aus.
    

7. Um sich die Zusammenhänge grafisch zu veranschaulichen, klicken Sie auf die Schaltfläche Darstellen.

Hinweise:

Es gilt darauf zu achten, dass die Einträge dem Datumsverlauf entsprechend eingetragen werden (Felder von links oben, nach rechts unten beschreiben), ansonsten erhalten Sie eine Fehlermeldung.
  

Allgemeines

 
Um die Eingabe eines beschriebenen Feldes zu löschen, fokussieren Sie es durch einen Klick mit der linken Maustaste in dieses und benutzen hierauf die Taste ENTF. Eine weitere Möglichkeit einzelne Eingaben zu löschen besteht darin, das Feld zu fokussieren, die rechte Maustaste zu bedienen und den Popupmenüeintrag Löschen zu wählen. Ferner ist es möglich eine Eingabe zu löschen, indem die Backslash-Taste bedient wird, und hierauf in ein anderes Feld geklickt wird. Um alle vorgenommenen Eingaben auf einmal zu löschen, benutzen Sie den Schalter Löschen.
 

Möchten Sie Tabellenwerte speichern, so kann dies über den Menüeintrag Datei - Speichern durchgeführt werden. Um mit bereits gespeicherten Daten eine Analyse durchführen zu lassen, verwenden Sie den Menüeintrag Datei - Öffnen. Beim Öffnen einer Datei werden bereits eingegebene Werte durch die Dateidaten überschrieben!

Nach einer Bedienung der Schaltfläche Schließen kehren Sie wieder zum Hauptformular des Unterprogramms zurück.
 

Diagramme

 
Ausgegebene Diagramme können per Mausbedienung gezoomt werden.

Zoomen (Koordinatenwertebereich verkleinern)

Klicken Sie mit der linken Maustaste in den Darstellungsbereich des Diagramms und ziehen Sie unter Festhalten der Taste ein Rechteck auf (von links nach rechts und von oben nach unten). Nach dem Loslassen der Maustaste wird der umrandete Bereich auf den Gesamtdarstellungsbereich vergrößert.

Urzustand

Möchten Sie den Koordinatenwertebereich wieder in den Urzustand versetzen, so klicken Sie mit der linken Maustaste in den Darstellungsbereich des Diagramms und ziehen unter Festhalten der Taste ein Rechteck auf (von rechts nach links und von unten nach oben). Nach dem Loslassen der Maustaste wird der ursprüngliche Gesamtdarstellungsbereich wiederhergestellt.
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Zinsrechnung

Annuitätentilgung

Zinseszinsrechnung grafisch

 

 
Beispiel 1 - Einzahlung:

Am 31.12 des Vorjahres beträgt das Kapital 0 €.

Nach der Aktivierung des Kontrollschalters Einzahlung, der Zuweisung eines (stetigen) Jahreszinssatzes von 10% im Eingabefeld Zinssatz, der Festlegung der folgenden Einzahlungen:

Datum	Betrag
01.03	100 €
05.04	200 €

durch die Eingabe der entsprechenden Datumsangaben und Zahlenwerte in die Tabelle, der Aktivierung der Kontrollschalter 360 Tage sowie Einzahlung und einer Deaktivierung des Kontrollkästchens Schaltjahr, erhalten Sie nach einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse für die entsprechenden Zeiträume:

Vom 01.03 bis 04.04 (Anzahl Tage: 35)
Guthaben: 100 EUR
Zins: 0,97 EUR

Vom 05.04 bis 31.12 (Anzahl Tage: 271)
Guthaben: 300 EUR
Zins: 22,50 EUR
 

Für den Stand am 31.12. des aktuellen Jahres wird ausgegeben:

Guthaben: 300,00 EUR
Jahreszins gesamt: 23,47 EUR
Gesamtguthaben: 323,47 EUR
 

Hinweis:

Auf dem Konto befand sich vom 31.12. des vorigen Jahres bis zum 28.02. des aktuellen Jahres kein Guthaben.
 

Beispiel 2 - Kontostand:

Am 31.12 des Vorjahres beträgt das Kapital 0 €.

Nach der Aktivierung des Kontrollschalters Kontostand, der Zuweisung eines (stetigen) Jahreszinssatzes von 10% im Eingabefeld Zinssatz, der Festlegung der folgenden Kontostände:

Datum	Kontostand
07.02	100 €
29.03	300 €
30.04	200 €
07.05.	440 €
09.07	880 €
01.10	300 €
12.12	50 €

durch die Eingabe der entsprechenden Datumsangaben und Zahlenwerte in die Tabelle, der Aktivierung der Kontrollschalter 360 Tage sowie Einzahlung und einer Deaktivierung des Kontrollkästchens Schaltjahr, erhalten Sie nach einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse für die entsprechenden Zeiträume:

Vom 07.02 bis 28.03 (Anzahl Tage: 50)
Guthaben: 100 EUR
Zins: 1,39 EUR

Vom 29.03 bis 29.04 (Anzahl Tage: 32)
Guthaben: 300 EUR
Zins: 2,67 EUR

Vom 30.04 bis 06.05 (Anzahl Tage: 7)
Guthaben: 200 EUR
Zins: 0,39 EUR

Vom 07.05 bis 08.07 (Anzahl Tage: 63)
Guthaben: 440 EUR
Zins: 7,70 EUR

Vom 09.07 bis 30.09 (Anzahl Tage: 84)
Guthaben: 880 EUR
Zins: 20,53 EUR

Vom 01.10 bis 11.12 (Anzahl Tage: 72)
Guthaben: 300 EUR
Zins: 6,00 EUR

Vom 12.12 bis 31.12 (Anzahl Tage: 20)
Guthaben: 50 EUR
Zins: 0,26 EUR

Für den Stand am 31.12. des aktuellen Jahres wird ausgegeben:

Guthaben: 50,00 EUR
Jahreszins gesamt: 38,94 EUR
Gesamtguthaben: 88,94 EUR

Hinweis:

Auf dem Konto befand sich vom 31.12. des vorigen Jahres bis zum 07.02. des aktuellen Jahres kein Guthaben.
 
 

 

Beispiel 1


Beispiel 2

   
 

 



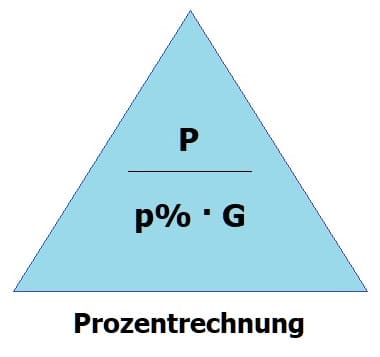
1. Prozentrechnung

Bei der Prozentrechnung (bzw. dem Prozentrechnen) werden Bezugszahlen als Grundwerte bezeichnet. Zu vergleichende Zahlen tragen die Bezeichnung Prozentwerte. Die Zahl, mit der in diesem Fall verglichen wird, wird als Grundwert G bezeichnet. Er ist das Ganze, auf welches sich Pozentangaben beziehen. Der Grundwert entspricht stets 100%.

Als Prozentwert P wird diejenige Zahl bezeichnet, die verglichen wird. Die obig gezeigte Darstellung trägt die Bezeichnung Formeldreieck.

Formel:

Prozentwert P = Prozentzahl / 100 · Grundwert

Das Verhältnis, welches aus dem Prozentwert und dem Grundwert gebildet wird, multipliziert mit der Zahl 100 ergibt den Prozentsatz (die Prozentzahl). Der Prozentsatz p gibt an, um wie viel Prozent sich ein Anfangswert ändert.

Prozentpunkt: Mit dem Begriff Prozentpunkte wird die absolute Differenz bezeichnet, die zwischen zwei Prozentzahlen besteht. Für den Prozentsatz gilt:
 
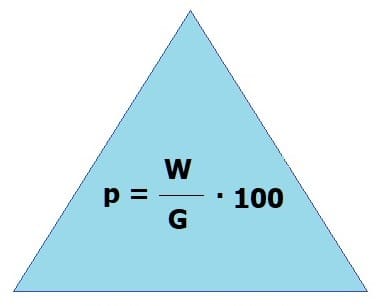
Prozentsatz p = Prozentwert / Grundwert (in %)

bzw.

Prozentsatz p = Prozentzahl / Grundwert · 100 (in %)
 

 
Als bequeme Prozentsätze werden Prozentsätze bezeichnet, die sich in einfacher Form als Brüche schreiben lassen. Beipiele hierfür sind:

50 % = 1/2
33,333 % = 1/3
25 % = 1/4
20 % = 1/5
10 % = 1/10
5 % = 1/20
 
Prozentualen Anteil berechnen: Ein prozentualer Anteil (Prozentanteil) ist ein relativer Anteil, der in Prozent ausgedrückt wird. Beim Prozentrechnen stehen Prozentsatz, Grundwert und Prozentwert in Relation zueinander.
 
Mit dem Wort Prozent wird das Hundertstel einer Zahl beschrieben. Es stammt aus dem Lateinischen und lautet übersetzt "von Hundert". Prozentangaben dienen dazu,Teile eines Ganzen festzulegen. Eine Prozentangabe stellt einen Vergleich zwischen zwei Zahlen an.

Das Prozent wird mit dem Zeichen % gekennzeichnet, welches die Bezeichnung Prozentzeichen trägt. Prozentangaben werden mittels diesem Zeichen kenntlich gemacht. Zwischen der Zahl und dem Prozentzeichen wird ein Leerzeichen gesetzt. Als Prozentzahl (Prozentpunkt) wird die Zahl vor dem Prozentzeichen bezeichnet.
 
Ein Prozent eines Grundwerts ist der hundertste Teil dessen. Nachfolgend aufgeführt sind die Prozentformeln (Grundformeln):








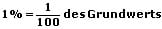
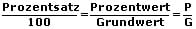
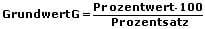
Als Prozentzahl wird die Angabe eines Prozentwerts ohne die Verwendung des Prozentzeichens bezeichnet. Diese Zahl geteilt durch 100 entspricht dem Ergebnis der Division des Prozentwerts P durch den Grundwert G (siehe Formel oben).

Prozentuale Anteile: Als prozentualer Anteil wird ein relativer Anteil bezeichnet, der in Prozent ausgedrückt wird.

Wandlung einer Prozentzahl in eine Dezimalzahl:

Um eine Prozentzahl z in eine Dezimalzahl umzurechnen, wird die Prozentzahl durch 100 geteilt.

Es gilt: z % = z / 100

Beispiel:
34% = 34/100 = 0,34

Wandlung einer Dezimalzahl in eine Prozentzahl:

Um eine Dezimalzahl d in eine Prozentzahl z zu wandeln, wird die Dezimalzahl in einen Bruch mit dem Nenner umgewandelt. Hierbei wird die Dezimalzahl mit dem Wert 100 erweitert:

Es gilt: d = (100 · d)/ 100

Beispiel:
0,72 = (100 · 0,72) / 100  = 72%
 
Die prozentuale Änderung (prozentuale Veränderung) beschreibt die Veränderung einer Größe, die innerhalb eines bestimmten Zeitraums vonstatten geht. Es gilt:

Endwert = Anfangswert ± prozentuale Veränderung

Eine prozentuale Veränderung wird durch den Prozentfaktor q ausgedrückt. Dies ist der Wert, der angibt, auf wieviel Prozent sich ein Anfangswert verändert hat.

Ist der Prozentfaktor größer als 1, so liegt eine prozentuale Zunahme (ein prozentualer Zuwachs, eine prozentuale Erhöhung, eine prozentuale Steigerung bzw. ein prozentualer Anstieg oder ein prozentuales Wachstum) dessen vor. Ist er hingegen kleiner als 1, so handelt es sich um eine prozentuale Abnahme (prozentualer Rückgang) dessen. Für den Endwert gilt:
 
Endwert = Anfangswert · Prozentfaktor q

Für den Prozentfaktor q gilt:

q = (100 % ± p %)

bzw.

q = (1 ± p/100)


Die prozentuale Abnahme berechnet sich mit:



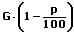
Die prozentuale Zunahme berechnet sich mit:




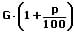
Eine prozentuale Differenz (ein prozentualer Unterschied) beschreibt die Differenz zwischen zwei Prozentzahlenwerten P1 und P2. Mit der nachfolgend gezeigten Formel kann dieser Wert ermittelt werden:

Prozentuale Differenz (prozentualer Unterschied) = ((P2-P1)/P1) · 100

Ist die prozentuale Differenz > 0, so handelt es sich um eine prozentuale Zunahme (Steigerung). Ist sie hingegen negativ, so liegt ein prozentualer Rückgang vor.


Nachfolgend aufgeführt sind einige Beispiele mit Hilfe derer anhand der Lösung von Prozentaufgaben die Anwendung der Prozentrechnung nachvollzogen werden kann.

Beispiele zum Prozentfaktor:

Beispiel 1:

Vor einem Jahr kostete ein Artikel 20 €. Sein Preis erhöhte innerhalb eines Jahres um 5%.
Wieviel kostet er heute?

Durch Ausklammerung wird der Prozentfaktor (100% + 5%) gebildet.
20 € + 20 € · 5% = 20 € ·(100% + 5%) = 21 €

Beispiel 2:

Vor einem Jahr kostete ein Artikel 20 €. Sein Preis erniedrigte innerhalb eines Jahres um 10%.
Wieviel kostet er heute?

Durch Ausklammerung wird der Prozentfaktor (100% - 10%) gebildet.
20 € - 20 € · 10% = 20 € ·(100% - 10%) = 18 €

Beispiele zur prozentualen Zunahme und Abnahme:

Beispiel 3:

Bei einer prozentualen Zunahme um 5 % gilt für den Prozentfaktor:
q = 100 % + 5 % = 105 % bzw. 1,05

Beispiel 4:

Bei einer prozentualen Abnahme um 5 % gilt für den Prozentfaktor:
q = 100 % - 5 % = 95 % bzw. 0,95


Allgemeine Beispiele zur Prozentrechnung:


Beispiel 1:

40% eines Geldbetrags von 200 Euro sind 40/100 · 200 Euro = 50 Euro.

Beispiel 2:

Von einem Artikel wurden binnen eines Jahres 300 Exemplare erzeugt. Dies entspricht einem Anstieg von 150% gegenüber dem Vorjahr. Wieviel Stück dessen wurden im Vorjahr hergestellt?

Gegeben sind:

Prozentwert: 300
Prozentsatz: 150

Der Grundwert errechnet sich wie folgt:



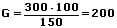
Somit wurden im Vorjahr 200 Stück produziert.
 

---

2. Promillerechnung

Die Promillerechnung basiert auf dem gleichen Prinzip wie die Prozentrechnung. Hierbei entspricht ein Promille eines Grundwerts dem tausendsten Teil dessen. Promilleangaben werden durch das Promillezeichen ‰ gekennzeichnet. Promillewert: Ein Promille entspricht 1/10 von einem Prozent oder 1/1000 des Grundwerts.
 
Nachfolgend aufgeführt sind die Promilleformeln:

 







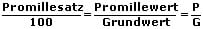
Beispiel:
 
5 ‰ einer Flüssigkeit von 100 Litern entsprechen 5/1000 · 100 Liter = 0,5 Liter

 
 

 

1. Bruch in Prozent - Prozent in Bruch

Bruch in Prozent:

Ein Prozent entspricht einem Hundertstel und somit dem Wert des Bruchs 1/100.

1% = 1/100

Ist der Nenner eines Bruchs auf die Zahl 100 erweiterbar, so kann die Prozentzahl nach einer Durchführung der Erweiterung aus dem Zähler des Bruchs abgelesen werden.

Beispiele:

1/25 = (1·4)/(25·4) = 4/100 = 4%       Multiplikation des Zählers und des Nenners des Bruchs mit der Zahl 4
3/25 =  (3·4)/(25·4) = 12/100 = 12%   Multiplikation des Zählers und des Nenners des Bruchs mit der Zahl 4

Liegt keine Erweiterbarkeit des Bruchs auf die Zahl 100 vor, wird der Zähler des Bruchs durch dessen Nenner geteilt und hierauf ein Prozentzeichen angehängt.

Beispiel:

3/16 = 0,1875 = 18,75%

Prozent in Bruch:

Ist eine Prozentangabe in einen Bruch zu wandeln, so ist lediglich die sich vor dem Prozentzeichen befindende Zahl durch die Zahl 100 zu teilen.

Beispiele:

12% = 12/100
37,5% = 37,5/100
 

---

 
2. Vermehrter Grundwert - Verminderter Grundwert


Vermehrter Grundwert:

Ein Grundwert kann sich durch eine Preiserhöhung oder durch eine Rabattaktion verändern. In einem solchen Fall erhöht sich der Grundwert.

Für den vermehrten Grundwert gilt folgende Formel:

Neuer Grundwert = Alter Grundwert  · (100 + Preiserhöhung in %) / 100

Beispiel:

Ein Artikel kostete bislang 200 Euro. Durch eine Preisanpassung in Höhe von 5% wird sein Verkaufspreis erhöht.

Somit errechnet sich sein neuer vermehrter Grundwert wie folgt:

(100 + 5) / 100 · 200 € = 105 / 100  · 200 € = 210 €.


Verminderter Grundwert:

Ein Grundwert kann sich auch durch eine Preissenkung verändern. Beim Vorliegen einer derartigen Gegebenheit erniedrigt sich der Grundwert.

Für den verminderten Grundwert gilt folgende Formel:

Neuer Grundwert = Alter Grundwert  · (100 - Preissenkung in %) / 100

Beispiel:

Ein Artikel kostete bislang 400 Euro. Durch einen Preisnachlass in Höhe von 3% wird sein Verkaufspreis gesenkt.

Somit errechnet sich sein neuer verminderter Grundwert wie folgt:

(100 - 3) / 100 · 400 € = 97 /100  · 400 € = 388 €.
  
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet der Mathematik, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
 
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
 

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Zinsrechnung sowie unter Wikipedia - Effektiver Jahreszins zu finden.

 

 

Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach

 

Unterprogramm Zinseszinsrechnung

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---