MathProf - Strahlensätze - Dreieck - Verhältnis - Streckenverhältnis

 

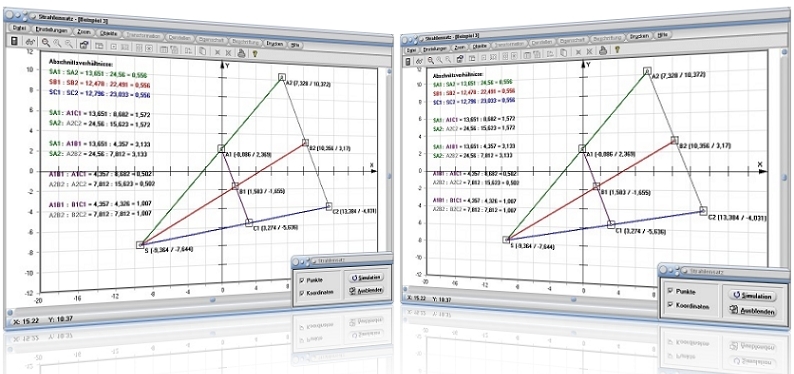
Modul Strahlensatz

---

Im Programmteil [Geometrie] - [Sonstiges (2D)] - Strahlensatz können Untersuchungen zum Strahlensatz durchgeführt werden.

 

Strahlensätze:
 
Die drei Strahlensätze befassen sich mit Streckenverhältnissen (Längenverhältnissen). Sie dienen dazu, Berechnungen von Teilstrecken, deren Längen nicht gemessen werden können, zu ermitteln und finden unter anderem bei der Bestimmung von Entfernungen Anwendung. Sie besitzen dann Gültigkeit, wenn zwei sich schneidende Geraden von zwei parallel verlaufenden Geraden geschnitten werden.

Sie lauten wie nachfolgend aufgeführt:

Werden die Strahlen eines Strahlenbüschels von Parallelen geschnitten, so verhalten sich die Abschnitte auf
 

• einem Strahl wie die gleichliegenden auf jedem anderen (Strahlensatz 1 oder 1. Strahlensatz)

• den Parallelen wie die entsprechenden Scheitelstrecken auf irgendeinem Strahl (Strahlensatz 2 oder 2. Strahlensatz)

• der einen Parallelen zueinander wie die gleichliegenden auf den anderen Parallelen (Strahlensatz 3 oder 3. Strahlensatz)

Folgende Voraussetzungen müssen erfüllt sein, um Strahlensätze anwenden zu können:

 - Es müssen zwei Strahlen vorhanden sein, die über einen gemeinsamen Punkt (Scheitelpunkt) verfügen
 - Beide Strahlen müssen von zwei zueinander parallel verlaufenden Geraden geschnitten werden
 - Keine der beiden parallel zueinander liegenden Geraden darf durch den Scheitelpunkt verlaufen

Seitenverhältnisse - Streckenverhältnisse: Anwendung finden Strahlensätze unter anderem bei der Berechnung der Entfernung zweier Gebäude oder um die Höhe eines Turms zu berechnen.

Als Längenverhältnis (Streckenverhältnis) wird der Quotient zweier Streckenlängen bezeichnet.

Unter Seitenverhältnis wird das Verhältnis zweier unterschiedlich langer Seiten verstanden.

Ein Strahlensatz wird auch als Vierstreckensatz bezeichnet.
 
Figuren, die sich aus zwei Strahlen bilden, die einen gemeinsamen Anfangspunkt besitzen und die von zwei parallel verlaufenden Geraden geschnitten werden, werden Strahlensatzfiguren genannt.
 

Erster Strahlensatz (Formel - Gleichung):

Die Formel (Gleichnung) des ersten Strahlensatzes lautet:


Der erste Strahlensatz setzt die Proportion zweier Teilabschnitte eines Strahles (Teilstrecken) gleich dem Verhältnis der enstsprechenden Teilabschnitte eines zweiten Strahls.

Er besagt: Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden geschnitten, so verhalten sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden.

Zweiter Strahlensatz (Formel - Gleichung):

Die Formel (Gleichnung) des zweiten Strahlensatzes lautet:


Der zweite Strahlensatz setzt die Proportion zweier Teilabschnitte eines Strahles (Teilstrecken) gleich dem Verhältnis zweier parallel liegender Strecken.

Er besagt: Werden zwei Strahlen mit gemeinsamen Anfangspunkt S von zwei parallelen Geraden und geschnitten, so verhalten sich die Parallelenabschnitte wie die zugehörigen Abschnitte auf jedem der Strahlen.
 
Die oben beschriebenen Sachverhalte können in diesem Unterprogramm analysiert werden.

 

 

Um eine konkrete Berechnung durchführen zu können, sind genau zwei Werte in dafür vorgesehene Eingabefelder einzutragen. Nach einer Bedienung der Schaltfläche Berechnen wird die zu ermittelnde Streckenlänge im entsprechenden Eingabefeld ausgegeben. Vor jeder Durchführung einer Berechnung muss die Schaltfläche Löschen bedient werden.

 

 
Neben der Durchführung von Berechnungen, ermöglicht es das Programm derartige Zusammenhänge interaktiv zu analysieren.

 

Um die Abschnittsverhältnisse (Längenverhältnisse) dargestellter Strecken zu verändern, führen Sie Folgendes aus:
 

1. Bedienen Sie die Schaltfläche Darstellen.
    

2. Klicken Sie in den rechteckig umrahmten Mausfangbereich eines Fangpunktes und bewegen Sie den Mauscursor bei gedrückt gehaltener Maustaste. Die Punkte S, A2 und C2 können an beliebige Positionen verschoben werden. Alle anderen Punkte können nur auf der Geraden verschoben werden, auf welcher sie positioniert sind.
    

3. Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. den Wert für die zu verwendende Schrittweite einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
    

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Anwendungsaufgaben genutzt werden. Dieses Programm kann auch dabei behilflich sein, einen Begriff zum entsprechenden Fachthema zu erklären.
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
 

• Punkte: Darstellung der Beschriftung der Mausfangpunkte ein-/ausschalten
• Koordinaten: Anzeige der Koordinaten der Mausfangpunkte ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Beispiel 1:

 

Werden in die Felder S-B1 und S-B2 die Werte 2 und 3 eingetragen, so gibt das Programm nach einer Bedienung der Schaltfläche Berechnen den relevanten Wert 1 im Eingabefeld B1-B2 aus.

 

Beispiel 2:

 

Bedienen Sie die Schaltfläche Darstellen und positionieren Sie die Mausfangpunkte der Strahlen an beliebige Positionen.

 

Bei Aufruf der Darstellung gibt das Programm für Längenverhältnisse aus:

 

SA1:SA2 = 8,682:15,62 = 0,556

B1:SB2 = 8,465:15,232 = 0,556

SC1:SC2 = 10:18 = 0,556

 

SA1:A1C1 = 8,682:8,012 = 1,084

SA2:A2C2 = 15,62:14,422 = 1,084

 

SA1:A1B1 = 8,682:4,027 = 2,156

SA2:A2B2 = 15,62:7,211 = 2,156

 

A1B1:A1C1 = 4,027:8,012 = 0,503

A2B2:A2C2 = 7,211:14,422 = 0,503

 

A1B1:B1C1 = 4,027:3,986 = 1,01

A2B2:B2C2 = 7,211:7,211 = 1,01

 

Unabhängig davon, an welche Position einzelne Punkte verschoben werden, bleiben folgende Längenverhältnisse stets konstant.

 

SA1:SA2 und SB1:SB2 und SC1:SC2

 

SA1:A1C1 und SA2:A2C2

 

SA1:A1B1 und SA2:A2B2

 

A1B1:A1C1 und A2B2:A2C2

 

A1B1:B1C1 und A2B2:B2C2
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3
   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
    

 

Hilfreiche Informationen zu diesem Fachthema sind unter der Adresse Wikipedia - Strahlensatz zu finden.
 

 

 

Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
 

 

Startfenster des Unterprogramms Strahlensatz
 

MathProf 5.0 - Unterprogramm Teilungsverhältnis

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---