PhysProf - Lichtbrechung - Brechzahl - Rechner - Lichtgeschwindigkeit

Fachthemen: Lichtbrechung - Lichtgeschwindigkeit - Brechzahl - Lichtquellen
PhysProf - Optik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Realschule, das Berufskolleg, das Gymnasium, das Studium sowie für alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Veranschaulichung des Verhaltens einer Lichtwelle, wenn diese von einem Medium in ein anderes übertritt.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul:Licht - Brechung - Brechungsgesetz - Refraktion - Brechung des Lichts - Snellius - Snelliussches Brechungsgesetz - Gesetz - Einfallswinkel - Ausfallswinkel - Lichtgeschwindigkeit - Ausbreitungsgeschwindigkeit - Lichtstrahl - Brechzahl - Brechungswinkel - Optik - Optisch - Strahlen - Lichtquelle - Lichtquellen - Natürliche Lichtquellen - Künstliche Lichtquellen - Lichtstrahlen - Planparallel - Planparallele Platte - Platte - Parallelverschiebung - Zeichnen - Lichtbrechung - Brechungszahl - Brechungsindex - Brechungsindizes - Beleuchtete Körper - Einheit - Physikalische Einheit - Grundlagen - Brechwinkel - Brechzahlen - n - Medium - Medien - Reflexion und Brechung - Prisma - Brechender Winkel - Ablenkung - Ablenkwinkel - Ablenkungswinkel - Ablenken - Lichteinfallswinkel - Winkel - Wirkung - Gesetzmäßigkeiten - Fermatsches Prinzip - Pierre de Fermat - Herleitung - Beweis - Optische Weglänge - Optischer Weg - Optische Dichte - Optisch dichter - Optisch dünner - Berechnen - Einführung - Abbe Zahl - Abbesche Zahl - Abbesche Theorie - Begriff - Begriffe - Flintglas - Kronglas - Was - Wie - Weshalb - Was ist - Warum - Erklärung - Einfach erklärt - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Aufgaben - Lösungen - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Physik - Physikalisch - Beispiel - Formel - Bild - Grafik - Grafische Darstellung |
 |  |
Lichtbrechung
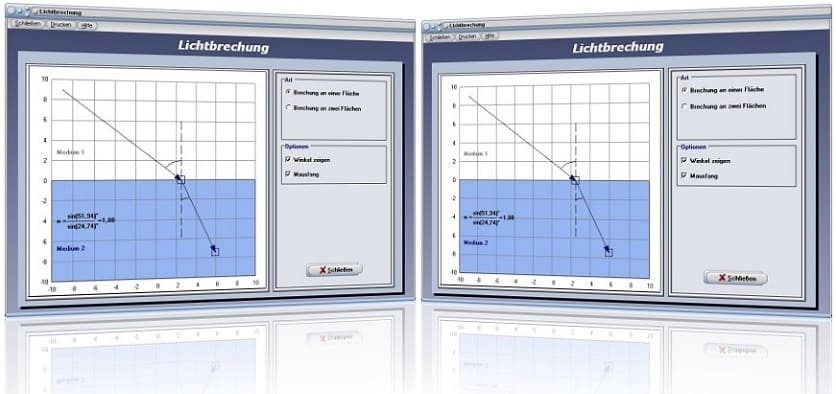
Modul Lichtbrechung
Das Programmmodul [Optik] - [Lichtbrechung] bietet die Möglichkeit das Verhalten einer Lichtwelle zu untersuchen, wenn diese von einem Medium in ein anderes übertritt.

Lichtbrechung - Abbildung 1

Lichtbrechung - Abbildung 2
Lichtstrahlen sind Linien, die als Modell zur Darstellung des Weges dienen, der vom Licht durchlaufen wird. Ein Lichtstrahl entstammt einem einzelnen Punkt von dem er sich geradlinig ausbreitet. Als beleuchtete Körper werden Körper bezeichnet, die selbst kein Licht aussenden, sondern vom Licht anderer Quellen beschieben werden.
Als Brechung (Refraktion) wird die Änderung der Ausbreitungsrichtung einer Lichtwelle beim Übergang von einem Medium in ein zweites bezeichnet, in welchem diese eine andere Ausbreitungsgeschwindigkeit besitzt. Tritt eine Lichtwelle an der Grenze eines Mediums in ein anderes über, so ändern sich Ausbreitungsgeschwindigkeit und Ausbreitungsrichtung. Dieser Vorgang wird als Lichtbrechung bezeichnet.
Die Brechzahl (der Brechungsindex, früher Brechungszahl) n ist eine optische Materialeigenschaft, die ein Maß für die Ausbreitungsgeschwindigkeit des Lichts in einem Medium ist.
Der Brechungswinkel (Brechwinkel oder brechender Winkel) beschreibt die Intensität, mit der ein Lichtstrahl beim Übergang von einem Medium in ein anderes abgelenkt wird.
Optische Dichte: Wenn ein Lichtstrahl auf seinem Weg von Medium 1 nach Medium 2 zum Einfallslot hin gebrochen wird, so besitzt Medium 1 eine kleinere optische Dichte und es ist optisch dünner. Im umgekehrten Fall ist dieses Medium optisch dichter.
Dies bedeutet: Als optisch dichter als ein anderer wird ein Stoff bezeichnet, wenn dieser eine größere Brechzahl als der andere dieser beiden besitzt. Eine andere Formulierung dieses Sachverhalts lautet: Das Medium, in welchem sich der kleinere dieser beiden Winkel befindet, wird als optisch dichter bezeichnet, bzw. das Medium, in dem sich der größere Winkel befindet, wird als optisch dünner angegeben.
1. Brechungsgesetz:
Mit Hilfe des Brechungsgesetzes von Snellius (Snelliussches Brechungsgesetz) kann die Größe der Richtungsänderung ermittelt werden. Dieses lautet:

Geht das Licht vom Vakuum (auch Luft) in ein anderes über, so gilt: (Der Wert n wird als Brechzahl definiert)

Hierbei sind:
α: Einfallswinkel (zum Lot) [rad]
β: Brechungswinkel (zum Lot) [rad]
c0: Lichtgeschwindigkeit (Ausbreitungsgeschwindigkeit) im Vakuum = 299 792 458 m/s
c1,c2: Lichtgeschwindigkeit in Medium 1 bzw. Medium 2 [m/s]
n,n1,n2: Brechzahlen bzw. Brechungsindizes
Die Bezeichnung des Winkels, der zwischen dem einfallenden Lichtstrahl und dem Einfallslot existiert, lautet Einfallswinkel (Lichteinfallswinkel). Der Ausfallswinkel ist derjenige Winkel, der sich zwischen dem reflektierten Strahl und dem Einfallslot bildet.
Die Stärke der Brechung hängt von den Ausbreitungsgeschwindigkeiten in den Medien ab. Beim Übergang vom dünneren zum dichteren Medium (höhere Brechzahl, geringere Lichtgeschwindigkeit) tritt Brechung zum Lot auf. Hierbei kann der Einfallswinkel einen materialabhängigen Grenzwert nicht überschreiten. Ist der Einfallswinkel größer als der Grenzwinkel, so tritt Totalreflexion ein. Hierbei wird die gesamte Lichtenergie in das erste, also dichtere Medium reflektiert.
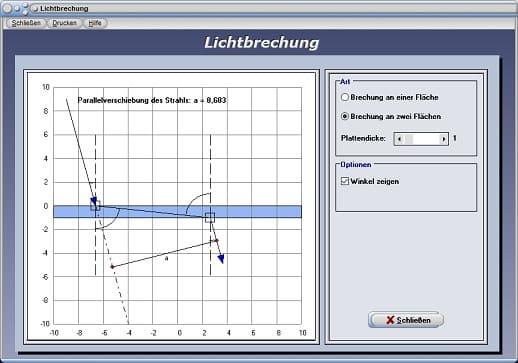
2. Planparallele Platte (Lichtbrechung an zwei parallelen Grenzflächen):
Beim Durchgang eines Lichtstrahls durch zwei planparallel liegende Flächen erfolgt keine Lichtbrechung, sondern lediglich eine Parallelverschiebung der Strahlen. Der Brechungswinkel an der ersten Grenzfläche entspricht in diesem Fall dem Einfallswinkel an der zweiten Grenzfläche. Es gilt:
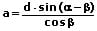
a: Parallelverschiebung des Lichtstrahls [m]
d: Plattendicke [m]
α: Einfallswinkel des Lichtstrahls an erster Grenzfläche
β: Einfallswinkel des Lichtstrahls an zweiter Grenzfläche
Programmbedienung
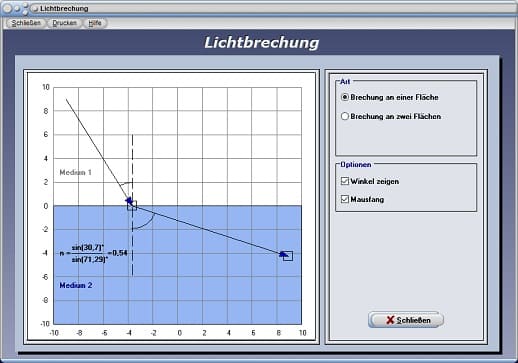
Lichtbrechung an einer Fläche:
Wählen Sie den Kontrollschalter Brechung an einer Fläche, so können Sie die Zusammenhänge analysieren, welche zur Ermittlung der Brechzahl führen. Fokussieren Sie hierbei einen Mausfangpunkt und bewegen Sie diesen, so wird die Brechzahl für zwei Medien, durch welche der Lichtstrahl dringt, ermittelt und ausgegeben. Liegt die Brechzahl bei einem Wert von 1,33, so würde dies den Fall darstellen, wenn der Lichtstrahl von Luft (Medium 1) in Wasser (Medium 2) dringen würde, da Luft eine Brechzahl von 1 und Wasser eine Brechzahl von 1,33 besitzt.
Lichtbrechung an zwei Flächen (planparallele Platte):
Die zweite Option in diesem Modul ermöglicht es, die Zusammenhänge, welche bestehen wenn Licht durch eine planparallele Platte dringt, zu untersuchen. Aktivieren Sie hierzu den Kontrollschalter Brechung an zwei Flächen.
Beim Durchgang durch eine planparallele Platte erfährt ein Lichtstrahl keine Richtungsänderung, sondern lediglich eine Parallelverschiebung. Die Größe der Verschiebung hängt hierbei vom Einfallswinkel und der Dichte der Platte ab. Wird die gewünschte Plattendicke mit Hilfe des Rollbalkens Plattendicke eingestellt und werden die Positionen der Mausfangpunkte verändert, so wird der Wert a für die Parallelverschiebung des Strahls ermittelt und ausgegeben.
Lichtgeschwindigkeit
Bei der Lichtgeschwindigkeit c handelt es sich um eine Konstante, welche von der Frequenz der Strahlung abhängig ist. Sie ist in allen Medien kleiner als im Vakuum. Im Vakuum besitzt die Lichtgeschwindigkeit den Wert c0 = 299 792 458 m/s.
In der nachfolgenden Tabelle ist die Lichtgeschwindigkeit in verschiedenen Stoffen aufgeführt:
| Medium | Lichtgeschwindigkeit c in km/s |
| Eis | 229 000 |
| Aceton | 221 000 |
| Ammoniak | 226 000 |
| Benzol | 200 000 |
| Brom | 181 000 |
| Chlor | 220 000 |
| Diamant | 122 000 |
| Ethanol | 220 000 |
| Flintglas | 186 000 |
| Kohlendioxid | 266 000 |
| Kronglas | 197 000 |
| Magnesiumoxid | 173 000 |
| Quarz | 194 000 |
| Steinsalz | 194 000 |
| Wasser | 224 000 |
Fermatsches Prinzip - Optische Weglänge
Das Fermatsche Prinzip (benannt nach Pierre de Fermat) besagt, dass der Weg, den das Licht bei einer Wellenausbreitung in einem Medium nimmt, um von einem Punkt zu einem anderen zu gelangen, stets so ist, dass die hierfür benötigte Zeit minimal ist. Es wurde vom französischen Mathematiker Pierre de Fermat (1601-1665) ermittelt.
Der geometrisch kürzeste Weg entspricht nicht stets dem zeitlich kürzesten Weg, da die hierfür benötigte Zeit von der Lichtgeschwindigkeit abhängt, die beim Durchdringen des entsprechenden Mediums vorliegt.
Als optische Weglänge (optischer Weg) wird die auf die Lichtgeschwindigkeit c im Vakuum bezogene Weglänge des Lichts bezeichnet, die in einem beliebigen optischen Medium (einer Materie) vorhanden ist.
In einem Medium mit konstantem Brechungsindex n gilt für die optische Weglänge: OWL = ns.
OWL: Optische Weglänge [m]
n: Brechzahl
s: Geometrische Weglänge [m]
Lichtbrechung am Prisma
Bei der Lichtbrechung am Prisma ist die gesamte Ablenkung des Lichtstrahls abhängig vom Einfallswinkel an der ersten Grenzfläche sowie vom brechenden Winkel an dessen zweiter Grenzfläche (siehe nachf. Abb.).
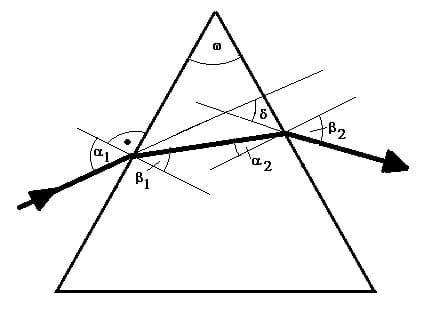
Für die Gesamtablenkung (den Ablenkwinkel bzw. Ablenkungswinkel) δ des Lichtstrahls gilt:
δ = α1 + β2 - ω
δ: gesamte Ablenkung des Lichtstrahls
α1: Einfallswinkel an erster Grenzfläche
β2: Brechungswinkel an zweiter Grenzfläche
n: Brechzahl
ω: brechender Winkel
Ein symmetrischer Stahlengang liegt vor, wenn α1 = β2. In diesem Fall kann zur Bestimmung der Brechzahl des Materials aus dem das Prisma besteht, die minimale Ablenkung δmin verwendet werden. Hierbei gilt:
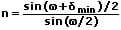
n: Brechzahl
δmin: geringste Gesamtablenkung
ω: brechender Winkel
Brechzahl
Nachfolgend aufgeführt ist die Brechzahlen (Brechungsindizes) für einige Medien. Die Angaben beziehen sich auf Luft bei 20°C und 1013 hPa für λ = 589,3 nm.
| Medium | Brechzahl |
| Ammoniak | 1,325 |
| Benzol | 1,5014 |
| Calciumoxid | 1,83 |
| Chlorbenzol | 1,527 |
| Diamant | 2,4173 |
| Ethanol | 1,3618 |
| Flour | 1,0002 |
| Glycerin | 1,455 |
| Leinöl | 1,486 |
| Magnesiumoxid | 1,736 |
| Methanol | 1,329 |
| Plexiglas | 1,491 |
| Polystyrol | 1,688 |
| Quarz | 1,544 |
| Quarzglas | 1,45886 |
| Rizinusöl | 1,478 |
| Steinsalz | 1,54425 |
| Terpentinöl | 1,47230 |
| Wasser | 1,33299 |
Als beleuchtete Körper werden Körper bezeichnet, die selbst kein Licht erzeugen oder ausstrahlen, sondern sich vom Licht anderer Quellen bescheinen lassen. Eine Lichtquelle ist ein Ort, von dem Licht ausgeht. Als Lichtquellen werden Gegenstände bezeichnet, die Licht aussenden. Es wird unterschieden zwischen:
- direkten Lichtquellen (Utensilien, die selbst leuchten)
- indirekten Lichtquellen (beleuchtete Körper, die Licht reflektieren und somit sichtbar werden)
Bei direkten Lichtquellen erfolgt eine weitere Unterteilung in:
- natürliche Lichtquellen
- künstliche Lichtquellen
Lichtquellen die in der Natur vorkommen, werden als natürliche Lichtquellen bezeichnet. Lichtquellen die hingegen von Menschen erzeugt werden, tragen die Bezeichnung künstliche Lichtquellen.
Beispiele für natürliche Lichtquellen:
Sonne
Sterne
Blitz
Feuer
Polarlichter
Beispiele für künstliche Lichtquellen:
Glühlampe
LED
Monitor
Laser
Leuchtstoffröhre
Fernseher
Die Abbe-Zahl (Abbesche Zahl) wird zur Charakterisierung der Eigenschaften von Gläsern eingeführt und wurde nach dem deutschen Physiker Ernst Abbe (1840 - 1905) benannt. Diese Zahl ist dimensionslos und eine Glaskonstante. Sie beschreibt wie sich die Geschwindigkeit sowie die Ausbreitungsrichtung in Abhängigkeit von der Wellenlänge beziehungsweise der Frequenz des das Glas durchdringenden Lichts abhängen. In der Augenoptik besitzt sie Werte im Bereich zwischen 20 (Flintglas) und 60 (Kronglas).
Die Stärke der Brechung des Lichts hängt von dessen Wellenlänge ab. Die Abbe-Zahl erteilt Auskunft darüber, wie die Streuung des Lichts in Abhängigkeit zum entsprechenden Brechungsindex steht. Je größer diese Zahl ist, desto geringer ist die Dispersion eines Materials und hierdurch auch der am Rand eines Glases auftretende Farbsaum. Glasmaterial ist umso hochwertiger, je höher die Abbe-Zahl ist. Der Kehrwert der Abbe-Zahl besitzt die Bezeichnung relative Dispersion.
Die Abbe-Zahl ist wie folgt definiert:
νe = (ne - 1) / (nF' - nC')
νe: Abbe-Zahl
ne,nF',nC': Brechungsindizes des Materials bei Wellenlängen der dazugehörenden Fraunhoferlinien
In der unten gezeigten Tabelle ist die Abbe-Zahl für einige Medien gelistet.
| Medium | Abbe-Zahl |
| Aceton | 52,01 |
| Anilin | 21,55 |
| Benzol | 30,2 |
| Diethylether | 55,14 |
| Essigsäure | 56,33 |
| Ethanol | 50,94 |
| Flintglas F3 | 36,94 |
| Flintglas SF4 | 27,52 |
| Flußspoat | 93,22 |
| Glycerin | 60,89 |
| Kalkspat | 48,95 |
| Kronglas FK3 | 65,69 |
| Kronglas BK1 | 63,63 |
| Kronglas BK 7 | 63,8 |
| Pyridin | 30,14 |
| Quarzglas | 67,41 |
| Steinsalz | 42,82 |
| Terpentinöl | 47,09 |
| Wasser | 55,76 |
Lichtbrechung - Abbildung 3
Lichtbrechung - Abbildung 4
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Brechung zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Reflexion - Zerstreuungslinse - Sammellinse - Hohlspiegel - Reflexion am Spiegel - Beugung am Spalt - Plancksches Strahlungsgesetz
Unterprogramm Lichtbrechung

PhysProf 1.1 - Unterprogramm RLC-Kreis

MathProf 5.0 - Unterprogramm Kurven in Parameterform

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















