PhysProf - Wellen - Simulation - Sinuswelle - Wellenlänge
Fachthema: Wellen
PhysProf - Mechanik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.
Online-Hilfe für das Modul
zur Untersuchung und Darstellung der Einflüsse von Parametern
auf das Verhalten von Transversalwellen bei Ausführung einer Wellensimulation.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul: |
 |  |
Wellen
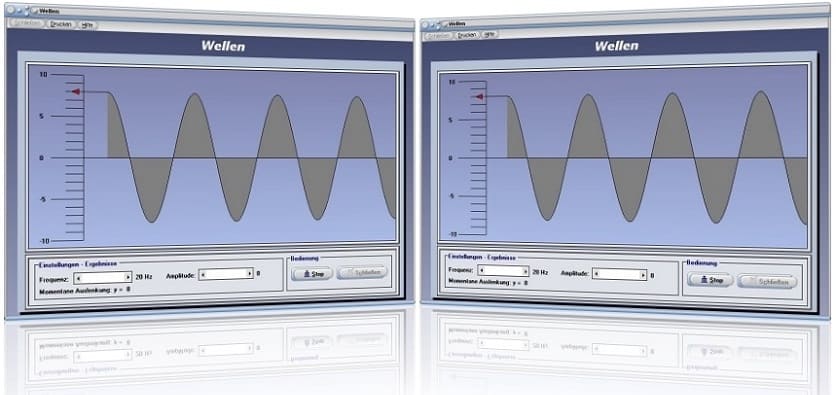
Modul Wellen
Mit Hilfe des kleinen Unterprogramms [Mechanik I] - [Wellen] können Einflüsse von Parametern, welche bei der Entstehung von Transversalwellen von Bedeutung sind, untersucht werden.
Wellen - Abbildung 1
Wellen - Abbildung 2
Mechanische Wellen: Als mechanische Welle wird ein Schwingungsvorgang bezeichnet der innerhalb eines Medium vonstatten geht. Hierbei werden zum Schwingen angeregte Teilchen, welche miteinander in Beziehung stehen, zur Ausführung von Schwingungen angeregt.
Der Begriff Wellenlänge λ beschreibt den Abstand zweier benachbarter Wellenberge gleicher Schwingungsphase. Die Ausbreitungsgeschwindigkeit (Phasengeschwindigkeit oder Wellengeschwindigkeit) von Wellen ist die Geschwindigkeit, mit der sich Wellen ausbreiten. Sie wird beschrieben mit:
c = λ / T = λ · f
T: Schwingungsdauer [s]
f: Frequenz [1/s]
λ: Wellenlänge [m]
Grundsätzlich kann physikalisch zwischen folgenden Wellenarten differenziert werden.
- Mechanische Wellen (Wasserwellen, Schallwellen)
- Elektromagnetische Wellen (Röntgenstrahlung, Licht)
- Quantenmechanische Wellen (Gravitationswellen, Materiewellen)
Hinsichtlich ihrer Ausbreitungsart wird entsprechend ihrer Schwingungsrichtung zwischen zwei Wellentypen unterschieden. Es sind dies:
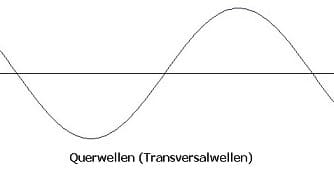
- Transversalwelle (Querwelle): Transversalwellen (Querwellen) sind Wellen, bei welchen die Richtung der Teilchengeschwindigkeit zur Richtung der Phasengeschwindigkeit senkrecht ist. Hierbei wechseln Wellenberge und Wellentäler. Als Wellental wird eine Vertiefung zwischen Wellenkämmen bezeichnet. Ein Wellenberg ist eine Erhöhung zwischen Wellenkämmen. Als Beispiel für eine derartige Welle sei Licht aufgeführt, welches sich im Vakuum ausbreitet.
- Longitudinalwelle (Längswelle): Longitudinalwellen (Längswellen) sind Wellen, bei welchen die Richtung von Phasengeschwindigkeit und Schwingungsgeschwindigkeit gleich ist (in ihnen wechseln Verdichtungen und Verdünnungen). Es handelt sich hierbei um Druckwellen, die sich mit Überdruck oder Unterdruck fortpflanzen. Als Beispiel für Longitudinalwellen seien Schallwellen genannt, die sich in Flüssigkeiten oder Gasen ausbreiten.
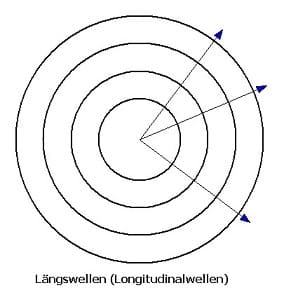
Bei Wasserwellen handelt es sich um eine Kombination von Transversalwellen und Longitudinalwellen. Elektromagnetische Wellen sind Wellen, die sich aus ineinandergreifenden magnetischen und elektrischen Feldern zusammensetzen.
Der Begriff gegenphasig charakterisiert die Eigenschaft zweier Wellen, gegeneinander um ein Vielfaches von π (180°) in deren Phasenlage verschoben zu sein. Als gleichphasig wird die Eigenschaft zweier Wellen bezeichnet, gegeneinander um ein Vielfaches von 2π (360°) in deren Phasenlage verschoben zu sein.
Als Wellenzahl ν wird (u.a bei elektromagnetischen Wellen) der Kehrwert der Wellenlänge bezeichnet. Unter anderem in der Spektroskopie gilt für sie:
ν = v/c = 1/λ
Sie ist der Quotient, der sich aus der Anzahl n der auf die Länge x entfallenden Wellenlängen und der Länge x bildet. Angegeben wird sie üblicherweise in der Einheit 1/cm.
Als Kreiswellenzahl k wird der Kehrwert der Wellenlänge multipliziert mit dem Faktor 2π bezeichnet. Sie entspricht der Länge des Wellenvektors. Für sie gilt:
k = ω/c
k = 2π/λ
ν: Wellenzahl [1/m]
k: Kreiswellenzahl [1/m]
v: Frequenz [1/s]
c: Ausbreitungsgeschwindigkeit der Welle [m/s]
λ: Wellenlänge [m]
ω: Kreisfrequenz (ω = 2πf) [1/s]
Hinweis:
Die Kreiswellenzahl wird häufig fälschlicherweise als Wellenzahl bezeichnet. Dies ist nicht korrekt und kann zu Missverständnissen führen.
Als Auslenkung (Elongation) wird bei einer Schwingung die augenblickliche Distanz eines Punktes P von seiner Ruhelage bezeichnet.
Unter dem Begriff Amplitude wird in der Physik und der Technik die Auslenkung (Elongation) einer periodischen Funktion oder eines zeitabhängigen Signals verstanden. Sie ist die maximale Auslenkung, die bei einer harmonischen Schwingung bezüglich derem arithmetischen Mittelwert auftritt.
Ein Wellenpaket (eine Wellengruppe) entsteht durch die Überlagerung mehrerer Wellen. Es kann als kombiniertes System einfacher Wellen interpretiert werden.
Als harmonische Wellen werden Wellen bezeichnet, die einen periodischen Verlauf besitzen und durch die trigonometrischen Funktionen Sinus und Cosinus beschrieben werden können. Als Kreiswellen werden Wellen bezeichnet, deren Teilchen sich auf Kreisbahnen bewegen.
Als Gangunterschied wird der Wegunterschied (die Wegdifferenz) zweier oder mehrerer zusammenhängender Wellen bezeichnet.
Bei einer Elementarwelle handelt es sich um eine Welle, die sich kreis- bzw. kugelförmig um ihren Mittelpunkt ausbreitet.
Bei der Wellenausbreitung innerhalb eines Mediums handelt es sich bei der Wellenfront um eine Fläche, auf welcher alle Punkte die gleiche Zeit benötigen, um zu einem Sender zu gelangen.
Wanderwellen: Als Wanderwelle wird eine Welle bezeichnet, die sich auf einem eindimensionalen Medium in lediglich einer Richtung ausbreitet. Eine derartige Welle kann auch zwischen parallel verlaufenden Begrenzungen erscheinen.
Seismische Wellen: Bei seismischen Wellen (Oberflächenwellen) handelt es sich um Energiewellen, die durch einen plötzlichen Gesteinsbruch der Erde oder durch Explosionen freigesetzt werden. Sie beschreiben eine Art der Ausbreitung von Bewegungen die in Gasen, Flüssigkeiten und Festkörpern und damit die hierbei auftretende Bewegungsenergie.
Als Primärwellen (P-Wellen) werden die hierbei zuerst auftretenden Wellen bezeichnet. Die hierauf folgenden Wellen tragen die Bezeichnung Sekundärwellen (S-Wellen). Bei beiden dieser Arten handelt es sich um Raumwellen. Die Ausbreitungsgeschwindigkeit der S-Wellen ist geringer als die der P-Wellen.
Als ebene Welle wird im 3D-Raum eine Welle bezeichnet, deren Flächen mit gleichen Phasenwinkeln parallele Ebenen darstellen.
Die Wellenlehre beschreibt das Geschehen, wenn eine Welle meit einer anderen Welle, einem Teilchen oder einer Strömung zusammentrifft.
Huygenssches Prinzip - Elementarwellen - Wellenausbreitung
Das Huygenssche Prinzip, benannt nach Christiaan Huygens (1629 - 1695), einem der bedeutendsten Mathematiker und Physiker des 17. Jahrhunderts, besagt, dass jeder Punkt der Wellenfront eines Mediums als Ausgangspunkt einer neuen Welle betrachtet werden kann. Die dabei entstehenden Elementarwellen kommen zur Überlagerung (Superposition).
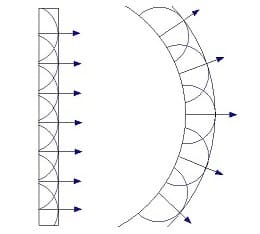
Hierdurch entsteht eine Wellenfront der einzelnen Elementarwellen. Diese neue Wellenfront ist die Einhüllende der einzelnen Elementarwellen. Die Ausbreitungsgeschwindigkeit der einzelnen Elementarwellen entspricht der Ausbreitungsgeschwindigkeit der Ursprungswelle. Dieses Prinzip gilt für alle Wellenarten.
Transversalwellen - Formeln
Eine Welle, die sich mathematisch durch eine Sinusfunktion beschreiben lässt, wird als Sinuswelle bezeichnet. Die Elongation (Ausbreitung) der in diesem Modul dargestellten Sinuswellen (Transversalwellen) kann mit Hilfe der Wellengleichung harmonischer Wellen, wie nachfolgend gezeigt, beschrieben werden.
bzw.
Eine Gleichung dieser Art wird in der Wellenlehre auch als Wellenfunktion bezeichnet. Sie beschreibt eine von Ort und Zeit abhängige Funktion, die einer Wellengleichung genügt.
Hierbei sind:
y: Elongation an Ort x zur Zeit t [m]
ymax: Amplitude der Welle [m]
ω: Kreisfrequenz (ω = 2πf) [1/s] bzw. [Hz]
t: Zeit [s]
x: Abstand vom Wellenzentrum [m]
c: Phasengeschwindigkeit [m/s]
T: Schwingungsdauer [s]
λ: Wellenlänge [m]
Programmbedienung
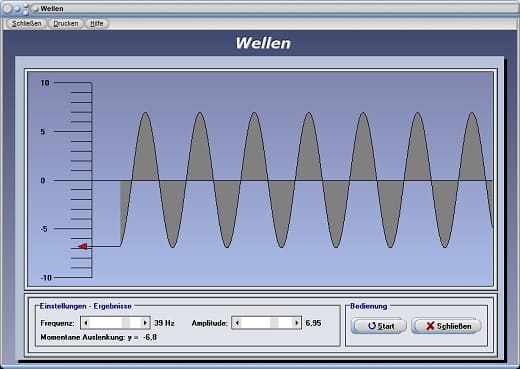
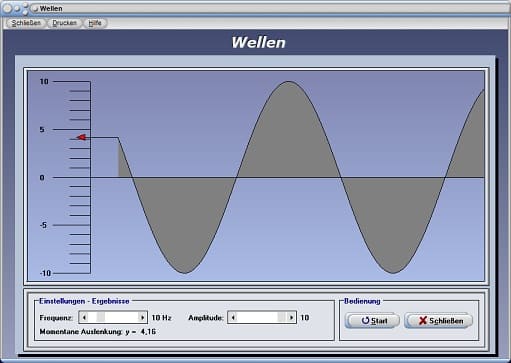
Beim Start dieses Moduls wird die Ausbreitung gleichmäßiger Transversalwellen simuliert.
Hierbei stehen Ausbreitungs- und Schwingungsrichtung aufeinander senkrecht. Wird nach dem Aufruf dieses Unterprogramms die Schaltfläche Stop bedient, so können die Einflussgrößen Frequenz und Amplitude mit Hilfe der dafür zur Verfügung stehenden Rollbalken eingestellt werden. Durch ein erneutes Bedienen dieser Schaltfläche wird die Simulation wieder mit den zugewiesenen Parameterwerten gestartet. Die vertikale Skalierung präsentiert die momentane lotrechte Elongation z.B. eines Seils, welche notwendig ist, eine Welle mit diesen Ausmaßen zu erzeugen.
Stehende Wellen
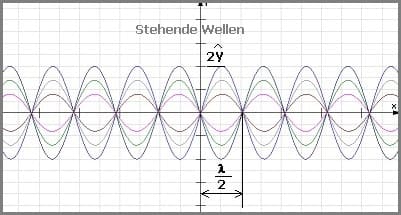
Die Überlagerung (Superpositionierung) von Wellen wird als Interferenz bezeichnet. Die Überlagerung zweier sich entgegengesetzt ausbreitender Wellen in einem Medium mit gleicher Frequenz, gleicher Amplitude sowie gleicher Wellenlänge wird als stehende Welle bezeichnet. Für die hinlaufende Welle gilt:
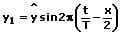
Für die entgegenlaufende Welle gilt:
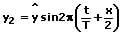
Aus diesen beiden Zusammenhängen ergibt sich für die resultierende Welle:
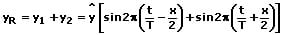
oder:
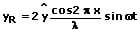
Bei entsprechenden Werten für x ist die Amplitude 2y für andere 0. An diesen Stellen findet keine Bewegung der Wellen statt, sie befinden sich stets am selben Ort und besitzen einen Abstand von λ/2 zueinander. Stellen bei welchen die Amplitude Null ist, werden als Knoten (Schwingungsknoten) bezeichnet.
Für Schwingungsknoten gilt:
D = (k+1/2)·λ/2
D: Abstand eines Schwingungsknotens vom Koordinatenursprung
mit k = 0, ±1, ±2 ...
Ein Schwingungsbauch entsteht bei einer stehenden Welle an einer Stelle maximaler Amplitude. Es ist der Bereich größter vertikaler
Auslenkung zweier Wellen. Es gilt:
D = k·λ/2
D: Abstand eines Schwingungsbauches vom Koordinatenursprung
mit k = 0, ±1, ±2 ...
Überlagerung (Interferenz) von Wellen
Zu einer Überlagerung (Interferenz oder Wellenüberlagerung) von Wellen kommt es, wenn mehrere Wellen ein Medium durchlaufen. Die resultierende Elongation einer derartigen Superpositionierung zweier Wellen kann wie folgt errechnet werden:
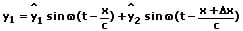
Δx: Gangunterschied der beiden Wellen
Δφ: Phasendifferenz der beiden Wellen
λ: Wellenlänge der beiden Wellen
Bei der Ausbreitung überlagerter (ebener) Wellen unterschiedlicher Wellenlänge wird zwischen den Phasengeschwindigkeiten einzelner Wellen und der Phasengeschwindigkeit des gesamten Wellenpakets unterschieden, die als Gruppengeschwindigkeit bezeichnet wird. Da sich einzelne Wellen eines derartigen Pakets in der Regel mit unterschiedlichen Geschwindigkeiten ausbreiten, bewegen sich Einzelwellen langsamer oder schneller als das gesamte Wellenpaket. Gruppengeschwindigkeit und Phasengeschwindigkeit sind identisch, wenn keine Überlagerung einzelner Wellen auftritt.
Die Bedingungen für die kleinste Gesamtamplitude der beiden Wellen lauten:
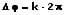
bzw.
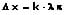
Die Bedingungen für die größte Gesamtamplitude der beiden Wellen lauten:
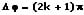
bzw.
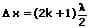
mit k = 0, ±1, ±2 ...
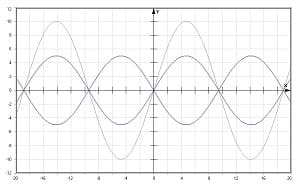
Abbildung 1 - Interferenz zweier Sinuskurven, die in Phase liegen
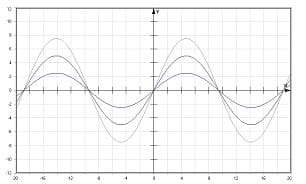
Abbildung 2 - Interferenz zweier Sinuskurven gleicher Amplitude, deren Phasendifferenz 180° (π) beträgt
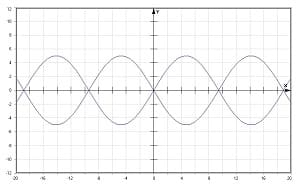
Abbildung 3 - Interferenz zweier Sinuskurven unterschiedlicher Amplitude, deren Phasendifferenz 180° (π) beträgt
Nachfolgend Beschriebenes gilt ausschließlich für harmonische Schwingungen, die dieselbe Frequenz, Amplitude und Ausbreitungsrichtung besitzen!
Destruktive Interferenz:
Treffen sich bei einem Phasenwinkel der Berg und das Tal zweier überlagerter Wellen, so löschen sich diese aus. Es wird von destruktiver Interferenz gesprochen. Eine destruktive Interferenz entsteht, wenn der Gangunterschied zweier Wellen die Werte λ/2, 3λ/2, 5λ/2 ... besitzt. Allgemein kann dieser Sachverhalt beschrieben werden mit:
Δx = (k-1/2)·λ
mit k = 0, ±1, ±2 ...
Konstruktive Interferenz:
Treffen sich bei einem Phasenwinkel die Berge oder Täler zweier überlagerter Wellen, so addieren sich deren Amplituden auf die Maximalauslenkung. In diesem Fall handelt es sich um eine konstruktive Interferenz. Eine konstruktive Interferenz entsteht, wenn der Gangunterschied zweier Wellen die Werte -2, -1, 0, 1, 2 ... besitzt. Für diesen Sachverhalt gilt:
Δx = k·λ
mit k = 0, ±1, ±2 ...
Kohärenz (Zusammenhang):
Kohärente Wellen verfügen über einen zeitlich konstanten Phasenunterschied. Lediglich Wellen die über eine gleiche Frequenz und Geschwindigkeit verfügen, können kohärent sein. Damit die sich bei einer Interferenz bildende Welle eine konstante Amplitude, Wellenlänge, Geschwindigkeit sowie Frequenz besitzt, müssen interferierende Wellen kohärent sein.
Energiedichte - Energiestrom - Mechanische Welle
Als mechanische Welle wird eine sich ausbreitende mechanische Schwingung bezeichnet, die Energie durch ein Medium überträgt. Wellen transportieren Energie. Diese wird in Form von Schwingungsenergie von Teilchen zu Teilchen innerhalb eines Mediums übertragen.
Unter dem Begriff Energiestrom wird die innerhalb eines Zeitraums durch eine Fläche strömende Energiemenge (beliebiger Form) verstanden. Als Energiedichte wird der Energiegehalt der Welle bezeichnet, der sich auf das Volumen des Mediums bezieht.
Für die Energiedichte gilt:
w = ρv²max/2
w: Energiedichte [J/m³]
ρ: Dichte des Mediums [kg/m³]
vmax: Maximale Schwinggeschwindigkeit der Teilchen [m/s]
Für die Energie, die während eines Zeitraums durch eine Fläche A strömt gilt:
E = Actρv²max/2
E: Strömende Energie [J]
A: Fläche [m²]
c: Ausbreitungsgeschwindigkeit der Welle [m/s]
ρ: Dichte des Mediums [kg/m³]
t: Zeit [s]
vmax: Maximale Schwinggeschwindigkeit der Teilchen [m/s]
Die Leistung P die hierbei erbracht wird, kann wie folgt berechnet werden:
P = Acw = ρAcv²max/2
P: Leistung [W]
c: Ausbreitungsgeschwindigkeit der Welle [m/s]
w: Energiedichte [J/m³]
A: Fläche [m²]
ρ: Dichte des Mediums [kg/m³]
vmax: Maximale Schwinggeschwindigkeit der Teilchen [m/s]
Die Intensität des Energiestroms ist wie nachfolgend gezeigt definiert:
J = cw = ρcv²max/2
P: Intensität [W/m²]
c: Ausbreitungsgeschwindigkeit der Welle [m/s]
w: Energiedichte [J/m³]
vmax: Maximale Schwinggeschwindigkeit der Teilchen [m/s]
Der Energiestrom beschreibt die (z. B. durch eine Fläche) strömende Energie je Zeiteinheit. Er wird auch als Energiestromstärke bezeichnet und besitzt dieselbe Einheit wie die Leistung (W).
Wellen - Abb. 3
Wellen - Abb. 4
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Welle zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
Unterprogramm Wellen
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
