MathProf - Datenanalyse - Datenauswertung - Mittelwert - Strichliste

Fachthema: Statistische Messwertanalyse - Messdaten - Messwerte - Messergebnisse
MathProf - Stochastik - Beschreibende Statistik - Software zur interaktiven Analyse und Darstellung wissenschaftlicher Zusammenhänge. Sie ermöglicht die Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung von statistischen Messwertanalysen zur Berechnung und Auswertung statistischer Kennzahlen von Messdaten.
In diesem Unterprogramm erfolgt das Berechnen hierfür wichtiger und relevanter Daten wie Kennzahlen und Streuungsmaße. Der implementierte Rechner ermittelt unter anderem die Werte für: Mittelwert, Median, Standardabweichung sigma, mittlerer Fehler des Mittelwerts, geometrisches Mittel, quadratisches Mittel (quadratischer Mittelwert), harmonisches Mittel, Variationskoeffizient, Streubreite und Varianz (mittlere quadratische Abweichung).
Bei der grafischen Darstellung der Auswertung der statistischen Analyse zu Bereich der deskriptiven Statistik ermöglicht das Programm die Ausgabe der Häufigkeitsverteilung in einem Histogramm (Häufigkeitsdiagramm) mit frei festlegbarer Klassenbreite sowie bei Bedarf das Plotten der Kurve der relevanten Normalverteilung.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind eingebunden.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Statistische Analyse - Daten - Messdaten - Statistische Kennzahlen - Statistische Kennwerte - Datenauswertung - Datenerfassung - Klassierte Daten - Datenanalyse - Datenreihe - Daten erheben - Datenerhebung - Daten erfassen - Zufall - Zufällig - Strichliste - Strichlisten - Statistische Daten - Intervall - Messergebnisse - Messwerte - Mittelwert - Modalwert - Zentralwert - Differenzwert - Medianwert - Minimum - Maximum - Geometrisches Mittel - Quadratisches Mittel - Standardfehler - Durchschnittliche Abweichung - Mittelwertbildung - Harmonisches Mittel - Standardabweichung - Abweichungen - Abweichung vom Mittelwert - Spannweite - Häufigkeitsdichte - Sigma - Histogramm zeichnen - Dispersionsmaß - Dispersionsmaße - Rohwert - Rohwerte - Häufigkeitsverteilung - Häufigkeitsverteilungen - Häufigkeitstabelle - Häufigkeitstabellen - Stichprobenvarianz - Mittlere quadratische Abweichung - Median - Klasseneinteilung - Grafische Darstellung - Grundlagen - Streuungsmaße - Zusammenhänge - Übersicht - Lagemaße - Lageparameter - Häufigkeiten - Statistische Kenngrößen - Prozent - Empirische Standardabweichung - Empirische Varianz - Empirischer Mittelwert - Standardfehler des Mittelwerts - Mittlere Abweichung - Mittlere absolute Abweichung - Mittlere lineare Abweichung - Mittlerer Fehler - Messung - Messungen - Ausreißer - Variationskoeffizient - Streubreite - Streumaße - Streuungsparameter - Standardmessfehler - Harmonischer Mittelwert - Durchschnitt - Durchschnittswert - Standardabweichungen - Klassenhäufigkeit - Lagemaß - Kennwerte - Wertepaare - Bewerten - Bewertung - Ermitteln - Bestimmen - Bestimmung - Bilden - Klassierung - Kenngröße - Kenngrößen - Einführung - Ergebnis - Begriff - Begriffe - Was - Wie - Weshalb - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Welche - Welcher - Welches - Wodurch - Beschreibung - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Definition - Streuungsmaß - Absoluter Fehler - Relativer Fehler - Prozentualer Fehler - Tabelle - Daten plotten - Graph - Grafisch - Bilder - Proben - Zusammenhänge - Darstellung - Grundlagen - Grundlegendes - Was ist - Was sind - Wieviel - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Auswertung - Auswerten - Stängel-Blatt-Diagramm - Stamm-Blatt-Diagramm - Berechnen - Formeln - Berechnung - Rechner - Bestimmung - Untersuchen - Plotten - Analyse - Untersuchung - Diagramm - Darstellen - Plotter - Symbol - Regel - Sigma-Intervall - Sigma-Umgebung - Sigma-Regel - Sigma-Regeln - Sigma Regel - Sigma Regeln - Herleitung - Beweis - Umgebung - Gleitender Durchschnitt - Gleitender Mittelwert - Gerichtete Abweichung - Linearer Mittelwert - Quadratischer Mittelwert - Geometrischer Mittelwert - Gewichteter Mittelwert - Ungewichteter Mittelwert - Getrimmtes arithmetisches Mittel - Getrimmter Mittelwert - Gewichtetes arithmetisches Mittel - Gewogenes arithmetisches Mittel - Ungewogenes arithmetisches Mittel - Statistische Auswertung - Statistische Berechnungen - Grafiken - Statistische Größen |
 |  |
Statistik - Statistische Messwertanalyse
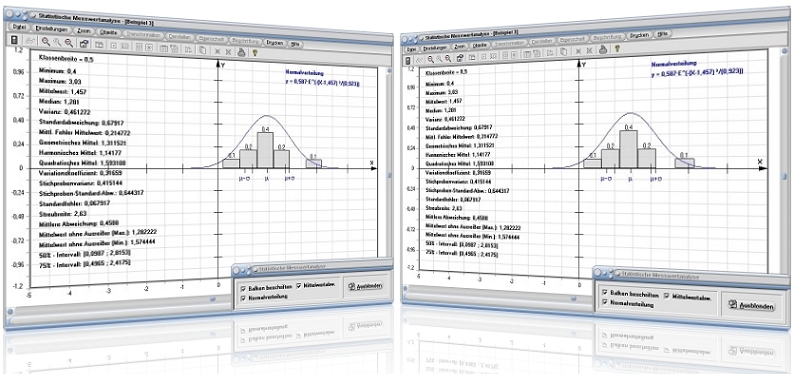
Modul Statistische Messwertanalyse
Mit Hilfe des Unterprogramms [Stochastik] - Statistische Messwertanalyse lässt sich eine statistische Auswertung von Messwerten durchführen. Grafische Darstellungen sowie numerische Berechnungen erlauben das Interpretieren (die Interpretation) entsprechender Sachverhalte und Zusammenhänge zu diesem Fachthema.

Statistik ist die Lehre der Methoden zum Umgang mit quantitativen Informationen. Sie befasst sich mit dem quantitativen Aufnehmen, Einteilen, Auswerten, Analysieren und Vorführen von Daten über Massen oder Bevölkerungen. Sie ist die Nutzung bestimmter Methoden zur Analyse empirischer Daten.
Die Grundlage einer statistischen Erhebung (Datenerhebung oder Datenerfassung) ist eine Menge von Objekten, von welchen ein oder mehrere Merkmale (Eigenschaften) untersucht werden. Dies kann durch Umfragen, Beobachtungen, Messungen oder Experimente vollzogen werden. Deren Auswertung erfolgt mit Hilfe stastistischer Verfahren.
Lageparameter bzw. Lagemaße (arithmetisches Mittel, Median, Mittelwert, Zentralwert) erteilen Auskunft darüber, innerhalb welchen Bereichs sich die auszuwertenden Daten befinden.
Streuungsparameter bzw. Streuungsmaße oder Streumaße wie die Spannweite, die mittlere Abweichung, die Varianz oder die Standardabweichung geben an, in welchem Maß sich die entsprechenden Daten vom Lageparameter unterscheiden. Die Spannweite entspricht der Distanz zwischen dem kleinsten und dem größten Wert eines Datensatzes.
Das Programm ermittelt aus den zur Verfügung gestellten Messwerten:
- Kleinster und größter Messwert (Minimum, Maximum)
- Median (Zentralwert oder Medianwert)
- Varianz (Mittlere quadratische Abweichung)
- Standardabweichung (quadratische Streuung, durchschnittliche Abweichung der Messwerte vom Erwartungswert)
- Mittlerer Fehler des Mittelwerts
- Geometrisches Mittel (Geometrischer Mittelwert)
- Quadratisches Mittel (Quadratischer Mittelwert)
- Harmonisches Mittel (Harmonischer Mittelwert)
- Variationskoeffizient
- Stichprobenvarianz
- Stichproben-Standardabweichung
- Standardfehler
- Streubreite
- Mittlere Abweichung (mittlere Differenz)
- Mittelwert (Zentralwert) ohne größten Ausreißer (Maximum)
- Mittelwert (Zentralwert) ohne kleinsten Ausreißer (Minimum)
- 50% - Intervall ] µ-2s ; µ+2s [ (Sigma-Intervall)
- 75% - Intervall ] µ-2s ; µ+2s [ (Sigma-Interval)
Nachfolgend aufgeführt und beschrieben sind wesentliche statistische Kennwerte (Lageparameter, Streuungsparameter), welche bei der Auswertung von Messwerten Verwendung finden.
Kennwerte - Kennzahlen - Zusammenhänge - Formeln - Grundlagen - Übersicht
Hinweis:
Nicht alle der im Folgenden aufgeführten Kennwerte werden in diesem Unterprogramm ermittelt, da sie zur Durchführung einer Messwertanalyse dieser Art in der Regel nicht von großer Relevanz sind. Eine Übersicht über alle in diesem Modul ermittelbaren Kennwerte ist zuvor aufgeführt.
1. Mittelwert (Zentralwert oder empirischer Mittelwert):

Das arithmetische Mittel ist der Quotient aus der Summe aller beobachteten Werte xi sowie der Anzahl der Beobachtungswerte n. Das arithmetische Mittel trägt auch die Bezeichnungen Zentralwert bzw. ungewichteter Mittelwert oder linearer Mittelwert bzw. arithmetischer Mittelwert oder empirischer Mittelwert.
2. Getrimmtes arithmetisches Mittel (getrimmter Mittelwert):
Dessen Ermittlung erfolgt wie beim Mittelwert (Zentralwert). Jedoch werden hierbei die k kleinsten sowie die k größten nicht zur Auswertung mit einbezogen. Es gilt: k << n/2.
3. Gewogenes arithmetisches Mittel (gewichtetes arithmetisches Mittel oder gewichteter Mittelwert):
Das gewogene arithmetische Mittel errechnet sich, wenn absolute Häufigkeiten H1 bis Hm einer Ausprägung gegeben sind, wie folgt:
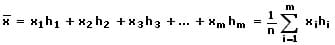
Dieses Mittel trägt auch die Bezeichnungen gewichtetes arithmetisches Mittel oder gewichteter Mittelwert.
4. Ungewogenes arithmetisches Mittel:
Das ungewogene arithmetische Mittel errechnet sich, wenn Beobachtungswerte x1 bis xm einer Ausprägung gegeben sind, wie folgt:
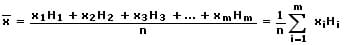
5. Gleitendes Mittel - Gleitender Durchschnittswert - Gleitender Durchschnitt - Gleitender Mittelwert:
Die Bildung des gleitenden Durchschnitts (gleitenden Mittelwerts bzw. Prognosewerts), ist eine Methode, mit welcher aus einer Anzahl von Werten aus der Vergangenheit und dem aktuellen Gegenwartswert xt ein Mittelwert MT gebildet wird. Dessen Berechnung kann wie folgt durchgeführt werden.
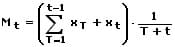
Der Begriff gleitendes Mittel trägt auch die Bezeichnungen gleitender Durchschnittswert, gleitender Durchschnitt oder gleitender Mittelwert.
6. Median:
falls n ungerade:

falls n gerade:

Als Median (Medianwert oder Zentralwert) wird der Wert bezeichnet, welcher sich exakt in der Mitte einer Datenverteilung befindet. Die Hälfte der Werte erfasster Messdaten liegt unterhalb dessen, die andere Hälfte derer ist größer.
7. Varianz (mittlere quadratische Abweichung):

Die Varianz oder mittlere quadratische Abweichung ist Maß für die Größe der Abweichung von einem Mittelwert. Sie beschreibt die Streuung der Daten um einen Mittelwert.
8. Standardabweichung (empirische Standardabweichung):

Die Standardabweichung (empirische Standardabweichung) beschreibt die durchschnittliche Abweichung aller gemessenen Werte von einem Mittelwert. Sie ist ein Maß für die Streuung der Werte einer Zufallsvariablen um ihren Mittelwert.
9. Mittlerer Fehler des Mittelwerts (Standardfehler des Mittelwerts):

Der mittlere Fehler des Mittelwerts (Standardfehler des Mittelwerts) erteilt Auskunft darüber, welche Abweichung der gesuchte Stichprobenmittelwert im Vergleich zum tatsächlichen Parameterwert besitzt und beurteilt somit die Stärke der Variabilität des arithmetischen Mittelwerts.
10. Harmonisches Mittel (harmonischer Mittelwert):

Das harmonische Mittel ist ein Mittelwert einer Menge von Zahlen, welcher dazu verwendet wird, um den Mittelwert von Verhältniszahlen (den Quotient zweier Größen) zu berechnen.
11. Quadratisches Mittel (quadratischer Mittelwert):

Quadratischer Mittelwert: Der quadratische Mittelwert (quadratisches Mittel) ist der Mittelwert, welcher als Quadratwurzel des Quotienten aus der Summe der Quadrate der beachteten Zahlen sowie ihrer Anzahl berechnet wird.
12. Geometrisches Mittel (geometrischer Mittelwert):

Der geometrische Mittelwert (geometrisches Mittel) ist der Mittelwert, welcher mit Hilfe der n-ten Wurzel aus dem Produkt der n betrachteten positiven Zahlen berechnet wird. Es ist stets kleiner oder gleich dem Wert des arithmetischen Mittels.
13. Variationskoeffizient (Verhältnis der Standardabweichung zum arithmetischen Mittel):

Der Variationskoeffizient ist eine statistische Kenngröße in der deskriptiven Statistik. Er ist definiert als Quotient aus Standardabweichung und dem arithmetischem Mittelwert.
14. Stichprobenvarianz (empirische Varianz):

Die Stichprobenvarianz (oder empirische Varianz) ist eine statistische Kennzahl für die Streubreite von Werten einer Stichprobe. In der deskriptiven Statistik die Kennzahl einer Stichprobe. Sie beschreibt die durchschnittliche quadratische Abweichung gemessener Beobachtungswerte von derem Mittelwert.
15. Standardfehler:

Der Standardfehler ist ein Maß für die mittlere Abweichung (dem Durchschnitt) des aus einer Stichprobe berechneten Mittelwerts vom tatsächlichen Mittelwert einer Grundgesamtheit.
16. Mittlere Abweichung
Die mittlere Abweichung (mittlere lineare Abweichung) wird durch die Aufsummierung der Abweichungen der Messwerte vom arithmetischen Mittel berechnet. Dieses Resultat wird hiernach durch die Anzahl erfasster Messwerte dividiert.
Mittlere absolute Abweichung (Betrag der mittleren Abweichung vom Mittelwert):

Die mittlere absolute Abweichung vom arithmetischen Mittel ist ein Streuungsmaß in der deskriptiven Statistik welches Auskunft darüber gibt, in welchem Maße eine Stichprobe um das arithmetische Mittel streut.
17. Streubreite:
Die Streubreite entspricht der Differenz zwischen Maximum und Minimum.
18. Mittelwert ohne Ausreißer (max):
Mittelwert x ohne größten (maximalen) Ausreißer.
19. Mittelwert ohne Ausreißer (min):
Mittelwert x ohne kleinsten (minimalen) Ausreißer.
20. 50%- bzw. 75%-Intervall (Sigma-Intervall):
Die Tschebyschow-Ungleichung gibt an, dass bei einer Wahrscheinlichkeitsverteilung mit Mittelwert μ und Standardabweichung σ mindestens 50% bzw. 75% der Werte im Intervall ] µ-2s ; µ+2s [ liegen.
21. Sigma-Regel (Sigma Regel):
Jedem Radius der Umgebung eines Erwartungswertes μ lässt sich eine bestimmte Wahrscheinlichkeit für diese Umgebung zuordnen. Der Radius dieser Sigma-Umgebungen wird als Vielfaches der Standardabweichung σ angegeben. Die σ-Umgebung des Erwartungswerts ist das Intervall [μ−σ ≤ X ≤ μ+σ]. Die 2σ-Umgebung dessen ist das Intervall [μ−2σ ≤ X ≤ μ+2σ] und die 3σ-Umgebung entspricht dem Bereich [μ−3σ ≤ X ≤ μ+3σ].
Die Werte für den Radius der Sigma-Umgebung für diese drei Bereiche sind folgende:
P(μ−σ ≤ X ≤ μ+σ) ≈ 68,3%
P(μ−2σ ≤ X ≤ μ+2σ) ≈ 95,4%
P(μ−3σ ≤ X ≤ μ+3σ) ≈ 99,7%
Sie werden als Sigma-Regeln (Sigma Regeln) bezeichnet. So besagt die erste dieser Regeln beispielsweise, dass sich ca. 68,3% der Merkmalswerte in einem Bereich um den Mittwert befinden.
22. Gerichtete Abweichung:
Unter einer gerichteten Abweichung wird eine Messabweichung verstanden, welche mit einem Vorzeichen versehen ist.
23. Absoluter Fehler:
Der absolute Fehler Δx beschreibt die Differenz zwischen dem gemessenen Istwert der Messgröße x (Messwert) und dem wahren Wert der gemessenen Größe xw.
Δx = x - xw
Der absolute Fehler hat die Dimension der Messgröße.
24. Relativer Fehler:
Da der wahre Wert einer Messgröße in keinem Fall in exakter Form bekannt ist, wird der Fehler (sofern der Fehler "genügend klein" ist) auf die Messgröße x bezogen.
Relativer Fehler = Absoluter Fehler / Wahrer Wert = Δx/xw
Relativer Fehler = Δx/x
Prozentualer Fehler bzw. relativer Fehler in % = Δx/x · 100
Mit:
n: Umfang der Stichprobe
xi: Einzelwerte
T: Jahreszahl
t: Zeitpunkt
25. Standardmessfehler:
Der Standardmessfehler ist diejenige statistische Kenngröße, die das Ausmaß des Messfehlers quantifiziert. Er gibt an, wie stark die Messfehler um die wahren Werte der Messgröße streuen.

SE: Standardmessfehler
Sx: Standardabweichung des Tests
rxx: Reliabilität der Testmethode
Fachbegriffe - Erklärung
Datenerfassung - Datenerhebung:
Unter dem Begriff Datenerhebung bzw. Datenerfassung wird die Methode zum Sammeln und Messen von Daten aus unterschiedlichen Quellen verstanden, die dazu dienlich sind, ein genaueres oder vollständiges Bild eines Zusammenhangs zu erhalten.
Datenanalyse - Datenauswertung:
Als Datenanalyse oder Datenauswertung wird der Ablauf der Gewinnung wertvoller Informationen aus Rohdaten bezeichnet. Hierbei werden Methoden angewandt mit Hilfe derer relevante Informationen gewonnen die tabellarisch und grafisch aufbereitet sowie dokumentiert werden.
Statistische Analyse:
Eine statistische Analyse wird durchgeführt um ein zugrunde liegendes Muster oder einen Trend zu erkennen. Hierzu werden große Mengen an Daten gesammelt, analysiert und gezeigt.
Statistische Auswertung:
Als statistische Auswertung wird die fachgerechte Untersuchung statistischer Daten bezeichnet, die mit Hilfe verschiedener Methoden gesammelt wurden. Als Beispiel zur Durchführung einer derartigen Untersuchung sei der Fragebogen aufgeführt.
Statistische Kennwerte - Statistische Kenngrößen:
Statistische Kennwerte besitzen die Funktion, in fusionierter Form Auskünfte über die Eigenschaften von Verteilungen zu geben. Kennwerte (Kenngrößen) werden auch als Maßzahlen oder statistische Kenngrößen bezeichnet. Zu ihnen zählen unter anderem der Modalwert, der Median, die Spannweite, der Mittelwert sowie das aritrhmetische Mittel.
Statistische Kennzahlen:
Bei Kennzahlen dieser Art handelt es sich um mengenbezogene angegebene Merkmale zu einer im jeweiligen Zusammenhang stehenden Wichtigkeit. Statistische Kennzahlen werden hinsichtlich Lagemaßen und Streumaßen unterschieden.
Statistische Daten:
Als statistische Daten werden Informationen bezeichnet, die durch eine Stichprobe oder eine Population ermittelt wurden und mit Hilfe statistischer Methoden analysiert wurden.
Lagemaß: Lagemaße sind Maße der zentralen Tendenz. Sie erteilen Aukunft darüber, bei welchem Wert das Zentrum einer Verteilung liegt. Zu den Lagemaßen zählen das arithmetische Mittel, das geometrische Mittel, der Modalwert, der Median sowie das Quantil.
Streuungsmaß (Dispersionsmaß): Streuungsmaße (Dispersionsmaße) erteilen Auskunft darüber, wie stark einzelne Werte voneinander oder von der zentralen Tendenz (der Breite der Verteilung) abweichen. Als Steuungsmaße werden die Varianz, die Standardabweichung, die Spannweite und die lineare Abweichung bezeichnet.
Klasseneinteilung - Klassierung von Daten:
Mit dem Begriff Klasseneinteilung oder Klassierung von Daten wird die Einteilung von Merkmalswerten oder Beobachtungswerten in getrennte Gruppen, Klassen oder Größenklassen benannt. Daten dieser Art werden als klassierte Daten bezeichnet.
Häufigkeiten: Als Häufigkeit wird die Anzahl eingetretener Ereignissen bezeichnet und somit das Resultat eines durchgeführten Zählvorgangs.
Häufigkeitsdichte: Die Häufigkeitsdichte einer Klasse stellt das Verhältnis der absoluten bzw. der relativen Häufigkeit einer Klasse zur entsprechenden Klassenbreite dar.
Ausreißer: Von einem Ausreißer wird gesprochen, wenn ein Messwert nicht in eine erwartete Messreihe passt oder im Allgemeinen nicht den Erwartungen entspricht.
Rohwert: Als Rohwerte werden die Ursprungswerte bezeichnet, die bei Durchführung einer Messung ermittelt werden und noch nicht umgeformt sind.
Differenzwerte: Als Differenzwert wird die Differenz zweier Messwerte bezeichnet, die zu zwei Zeitpunkten an derselben Stichprobe erhoben wurden.
Modus (Modalwert): Als Modus oder Modalwert wird der Wert bezeichnet, der in einer beobachteten Datenmenge am häufigsten auftritt.
Dispersionsmaß (Streuungsmaß): Das Dispersionsmaß oder Streuungsmaß ist eine Kennzahl dafür, in welcher Form sich ein Wahrscheinlichkeitsmaß oder eine Zufallsvariable verteilt.
Messwerte: Als Messwert wird der Wert einer Messgröße bezeichnet, der von einem Messgerät oder einer Messeinrichtung bezogen wird.
Messergebnisse: Als Messergebnis wird der durch Auswertung eines mit einer Messeinrichtung gewonnenen Messwerts bezeichnet.
Datenreihen: Als Datenreihe wird ein Satz von Daten bezeichnet, der in einem Diagramm ausgegeben wird.
Häufigkeitsverteilung: Als Häufigkeitsverteilung werden die Messwerte bezeichnet, die Auskunft darüber erteilen, mit welcher Häufigkeit (wie oft) ein bestimmter Messwert in einer statischen Analyse vorkommt.
Häufigkeitstabellen: In einer Häufigkeitstabelle werden die Häufigkeiten des Auftretens eines bestimmten Messwerts sowie die Werte eines Merkmals einander tabellarisch gegenüber gestellt.
Klassenhäufigkeit: Als Klassenhäufigkeit wird die Anzahl statistischer Einheiten mit Merkmalsausprägungen einer bestimmten Klasse bezeichnet.
Numerische Auswertung
Gehen Sie folgendermaßen vor, um die numerische Auswertung von Messwerten durchführen zu lassen:
- Geben Sie einen Messwert in das dafür vorgesehene Feld ein, bedienen Sie die Schaltfläche Übernehmen und wiederholen Sie diesen Vorgang, bis alle zur Auswertung erforderlichen Messwerte aufgenommen sind.
- Möchten Sie einen Eintrag in der Tabelle löschen, so fokussieren Sie diesen und bedienen die Schaltfläche Löschen. Soll ein bereits eingetragener Wert geändert werden, so fokussieren Sie zunächst den entsprechenden Eintrag in der Tabelle, geben den neuen Wert in das Feld ein und bedienen hierauf die Schaltfläche Ersetzen. Um alle Einträge zu löschen, kann die Schaltfläche Alle löschen verwendet werden.
- Bedienen Sie die Schaltfläche Berechnen, so werden die ermittelten Auswertungsergebnisse in der Tabelle Ergebnisse ausgegeben.
Hinweise:
Ein geometrisches Mittel existiert lediglich dann, wenn das Produkt aller definierter Messwerte > 0 ist. Ein harmonisches Mittel kann nur ermittelt werden, wenn keiner der Messwerte den Wert 0 besitzt.
Grafische Analyse

Ein Histogramm ist die grafische Darstellung der Häufigkeitsverteilung von Messwerten, anhand eines Balkendiagramms. Das Programm ermöglicht die Ausgabe eines solchen, nach Durchführung einer Messwertanalyse.
Um eine grafische Analyse der Messergebnisse durchzuführen, sollten Sie wie nachfolgend beschrieben vorgehen:
- Führen Sie zuvor Beschriebenes (Numerische Auswertung) aus, um Messwerte aufzunehmen.
- Soll die Klassenbreite des Histogramms vor dem Aufruf einer grafischen Darstellung festgelegt werden, so aktivieren Sie den Kontrollschalter Klassenbreite fix und geben den gewünschten Wert zur Festlegung der Klassenbreite in das hierfür zur Verfügung stehende Feld ein. Möchten Sie die Klassenbreite dessen jedoch bei Ausgabe der grafischen Darstellung einstellen, so aktivieren Sie den Kontrollschalter Klassenbreite variabel.
- Bedienen Sie die Schaltfläche Darstellen.
- Wurde Kontrollschalter Klassenbreite variabel aktiviert, so positionieren Sie den Rollbalken Klassenbreite, um die gewünschte Klassenbreite einzustellen.
- Um sich die Dichtekurve einer Gauß'schen Normalverteilung darstellen zu lassen, aktivieren Sie das Kontrollkästchen Normalverteilung.
Klicken Sie das Kontrollkästchen Mittelwertabw.an, so werden neben dem Mittelwert, zusätzlich die Differenz μ-σ und die Summe μ+σ der Standardabweichung bzgl. des Mittelwerts markiert.
- Wurde eine variable Klassenbreite gewählt, so besteht die Möglichkeit die Klassenbreite interaktiv durch eine Simulation verändern zu lassen. Um Zusammenhänge derart zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. den Wert für die zu verwendende Schrittweite einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
Ein Stamm-Blatt-Diagramm (Stängel-Blatt-Diagramm) verfügt über zwei Spalten. In dessen linker Spalte befinden sich die entsprechenden Äquivalenzklassen in der Form von Stämmen, auf der rechten Seite werden die in Form von Blättern dargestellten Merkmale eingetragen. Die Bildung relevanter Klassen erfolgt in der Regel entsprechend dem Dezimalsystem. Unterteilungen anderer Art sind ebenso möglich. Die zur Erstellung des Diagramms verwendete Einheit wird beim Diagramm ausgegeben.
Beispiel:
Es liege eine Messreihe vor, deren geordnete Daten nachfolgend aufgeführt sind:
0,2 0,5 1,5 1,5 1,6 1,7 2,2 3,2 3,3 3,4 3,7 4,4 4,8 4,9
Erfolgt eine Stamm-Einteilung derer nach natürlichen Zahlen, so ergibt sich folgendes Stamm-Blatt-Diagramm:
4 | 4 8 9
3 | 2 3 4 7
2 | 2
1 | 5 5 6 7
0 | 2 5
Einheit: 0,1
Als Einheit wird in diesem Fall die Zahl 0,1 festgelegt.
Strichlisten - Datenerhebung - Datenerfassung

Strichliste: Strichlisten werden beim Erfassen von Daten eingesetzt, um diese schnell und übersichtlich anzuordnen. Für jeden Fall wird ein vertikaler Strich gezeichnet. Bei jedem fünften Strich wird anstelle eines vertikalen Strichs ein Querstrich gezeichnet. Dies dient der Übersichtlichkeit.
Beispiel 1:
Bei der Durchführung eines Würfelspiels wurde 24-mal gewürfelt. Es ergaben sich folgende Resultate:

Die Zahl 1 wurde 3-mal gewürfelt.
Die Zahl 2 wurde 5-mal gewürfelt.
Die Zahl 3 wurde 4-mal gewürfelt.
Die Zahl 4 wurde 2-mal gewürfelt.
Die Zahl 5 wurde 5-mal gewürfelt.
Die Zahl 6 wurde 2-mal gewürfelt.
Beispiel 2:
Bei der Ziehung von Kugeln aus einer Urne wurden nachfolgende Ergebnisse erzielt.

Die Auswertung dieser Daten ergibt:
Es wurden 8 rote Kugeln gezogen.
Es wurden 6 grüne Kugeln gezogen.
Es wurden 11 blaue Kugeln gezogen.
Es wurden 3 weisse Kugeln gezogen.
Es wurden 5 gelbe Kugeln gezogen.
Es wurden 6 schwarze Kugeln gezogen.
Es wurden insgesamt 40 Kugeln gezogen.
Am häufigsten wurde eine blaue Kugel gezogen.
Am seltesten wurde eine weisse Kugel gezogen.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Datenverwaltung
Möchten Sie eingegebene Messwerte speichern, so kann dies über den Menüeintrag Datei - Speichern durchgeführt werden. Um mit bereits gespeicherten Daten eine Analyse durchzuführen, verwenden Sie den Menüeintrag Datei - Öffnen. Beim Öffnen einer Datei werden bereits eingegebene Werte durch die Dateidaten überschrieben!
Es besteht auch die Möglichkeit die auszuwertenden Daten in einer Excel-Tabelle zu definieren und hiernach zu importieren. Die Zahlenwerte sind hierbei nach folgendem Schema in der Excel-Tabelle festzulegen: In Spalte A der Excel-Tabelle legen Sie die Messwerte fest. Beginnen Sie mit der Eingabe im obersten Feld der Spalte.
Speichern Sie diese Tabelle hierauf in einer Datei ab, wählen Sie im Programm den Menüeintrag Datei - Excel-Daten importieren und öffnen Sie die entsprechende Datei. Eingelesen werden alle Werte bis zum ersten leeren Feld der Excel-Tabellen-Spalte.
Bedienformular

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellung vornehmen:
- Balken beschriften: Beschriftung des Balkendiagramms ein-/ausschalten
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Beispiel
Es gilt, nachfolgend aufgeführte Messwertergebnisse statistisch auswerten zu lassen:
1,234
1,756
1,141
1,244
3,030
1,822
1,514
1,318
1,111
0,400
Vorgehensweise und Lösung:
Nach Festlegung dieser und einer Bedienung der Schaltfläche Berechnen, erhalten Sie folgende Analyseergebnisse:
Anzahl der Messwerte: 10
Minimum: 0,4
Maximum: 3,03
Mittelwert: 1,457
Median (Zentralwert): 1,281
Varianz: 0,461272
Standardabweichung: 0,67917
Mittlerer Fehler des Mittelwerts: 0,214772
Geometrisches Mittel: 1,311521
Harmonisches Mittel: 1,14177
Quadratisches Mittel: 1,593108
Variationskoeffizient: 0,31659
Stichprobenvarianz: 0,415144
Stichproben-Standardabweichung: 0,644317
Standardfehler: 0,067917
Streubreite: 2,63
Mittlere Abweichung: 0,4588
Mittelwert ohne Ausreißer (max): 1,282222
Mittelwert ohne Ausreißer (min): 1,574444
50% - Intervall: ] 0,0987 ; 2,8153 [
75% - Intervall: ] 0,4965 ; 2,4175 [
Wird das Kontrollkästchen Normalverteilung bei Ausgabe der grafischen Darstellung der Zusammenhänge aktiviert, so gibt das Programm für die ermittelte Gleichung der Normalverteilung zudem aus:
Y = 0,587·e(-(x-1,457)²/0,923))

Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2

Grafische Darstellung - Beispiel 3

Grafische Darstellung - Beispiel 4

Grafische Darstellung - Beispiel 5

Grafische Darstellung - Beispiel 6

Grafische Darstellung - Beispiel 7

Grafische Darstellung - Beispiel 8
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Median
Wikipedia - Varianz
Wikipedia - Quadratisches Mittel
Wikipedia - Harmonisches Mittel
Kombinatorik - Urnenmodell - Pfadregel - Galton-Brett - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Regressionsanalyse - Stichproben - Stichproben - Verteilungen - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)
Startfenster des Unterprogramms Statistische Messwertanalyse
MathProf 5.0 - Unterprogramm Regressionsanalyse

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.















