MathProf - Strecke - 3D - Dreieck - Räumlich - Pyramide - Quader

Fachthemen: Strecke - Dreieck - Quader - Pyramide - Würfel - Im Raum
MathProf - Räumliche Geometrie - Mathematik zweidimensional und dreidimensional. Software zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Ausführung von interaktiven Untersuchungen mit Strecken im Raum, dem dreidimensionalen Dreieck im Raum, der quadratischen Pyramide im Raum sowie dem Quader und dem Würfel in einem dreidimensionalen Koordinatensystem.
Dieses Unterprogramm ermöglicht neben derer räumlichen Darstellung die Durchführung von Berechnungen mit geometrischen Gebilden dieser Art sowie die Praktizierung dreidimensionaler Simulationen zu diesem Themengebiet der Stereometrie.
Bei der Untersuchung einer Strecke im Raum erfolgt unter anderem die Ermittlung der euklidischen Distanz (euklidischer Abstand) zweier definierter Punkte.
Ferner lassen sich die Werte folgender Eigenschaften dieser Gebilde berechnen: Mittelpunkte von Strecken, Rauminhalt (Volumen) vom Quader, Rauminhalt (Volumen) der Pyramide und des 3D-Würfels, Flächeninhalt vom Dreieck im Raum, Oberfläche bzw. Mantelfläche einer quadratischen Pyramide, Oberfläche bzw. Mantelfläche vom Quader, Oberfläche bzw. Mantelfläche vom Würfel, Raumdiagonalen vom Würfel, Raumdiagonalen vom Quader sowie der Abstand zweier Punkte im Raum.
Nach einer Festlegung der Werte erforderlicher Größen führt der Rechner hierfür relevante Untersuchungen durch, ermittelt die Lösungen der gestellten Aufgabe, gibt die erforderten Ergebisse aus und stellt die entsprechenden Zusammenhänge grafisch dar. Dieses Unterprogramm ermöglicht das Berechnen der Werte vieler wichtiger Größen zu diesem Fachthema.
Ein frei bewegbares und drehbares 3D-Koordinatensystem erlaubt die Praktizierung interaktiver Analysen bzgl. Sachverhalten und relevanter Zusammenhänge zu diesem Fachthema.
Auch die Ausführung verschiedener Simulationen mit den entsprechenden Gebilden im 3D-Raum kann veranlasst werden. Neben der Ausgabe fachthemenrelevanter Darstellungen ermöglicht das Programm zudem das Einblenden zusätzlicher Koordinatenebenen.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:3D-Würfel - 3D-Quader - 3D-Dreieck - Dreieck im Raum - 3D - Pyramide - Quader - Kubus - Gerade quadratische Pyramide - Dreidimensional - Hexaeder - Würfel - Länge - Breite - Höhe - Kanten - Quadratische Säule - Vektoren - Raumgeometrie - 3D-Geometrie - Stereometrie - Geometrie im Raum - Euklidischer Abstand - Euklidische Distanz - Abstand Punkt Punkt - Abstand zwischen zwei Punkten - Entfernung zwischen zwei Punkten - Entfernung zweier Punkte - Abstand zweier Punkte im Raum - Distanz zweier Punkte - Gerade Pyramide - Schiefe Pyramide - Merkmale - Richtungswinkel - Strecke im Raum - Kantenlängen - Gemeinsamkeiten - Unterschiede - Oberfläche - Volumen - Pyramidenhöhe - Flächeninhalt - Räumliche Darstellung - Quadratische Pyramide - Quadratische Grundfläche - Quader zeichnen - Raumdiagonale - Diagonalen - Formelübersicht - Grundfläche - Deckfläche - Grundkante - Oberflächeninhalt - Rechteckige Pyramide - Geometrisch - Seiten - Herleitung - Beweis - Dreidimensionales Dreieck - Netze - Netz - Quadernetz - Würfelnetz - Körpernetz - Quadernetze - Würfelnetze - Körpernetze - Pyramidennetz - Schwerpunkt - Winkel - Oberflächenberechnung - Körperberechnung - Volumenberechnung - Seitenkanten - Teilflächen - Schnitt - Schrägbild - Seitenlängen - Rotierender Quader - Umfang - Grundseite - Mantelfläche - Flächendiagonale - Seite - Begriff - Begriffe - Räumlich - Fläche - Diagonale - Seitenkante - Seitenfläche - Raumdiagonalen - Kantenlänge - Grundkantenlänge - Seitenflächen - Koordinaten - Eckpunkte - Ecke - Ecken - Innenwinkel - Punkte - Gegeben - Gesucht - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Graph - Plotten - Grafisch - Mittelpunkt - Bild - Bedeutung - Was bedeutet - Welche - Welcher - Welches - Wodurch - Erklärung - Einfach erklärt - Beschreibung - Definition - Tabelle - Rechner - Berechnen - Beispiel - Aufgabe - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Grafik - Zeichnen - Bilder - Einführung - Untersuchen - Untersuchung - Darstellung - Berechnung - Formeln - Darstellen - Eigenschaften - Grafische Darstellung - Streckenlänge |
Strecke im Raum - Dreieck im Raum - Pyramide - Quader
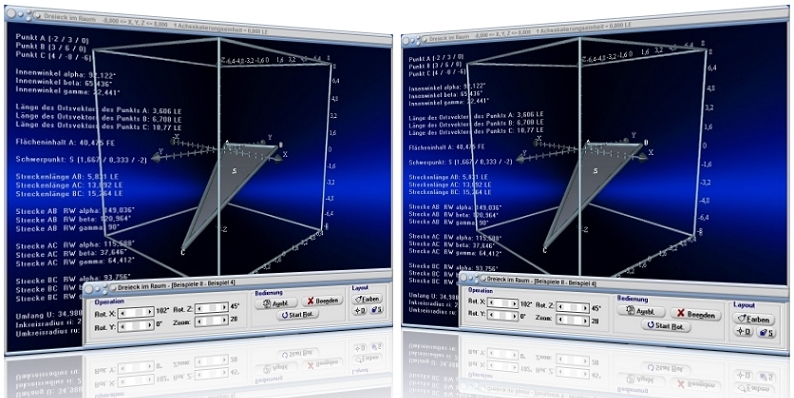
Modul Dreieck - Pyramide - Quader im Raum
Mit Hilfe des Unterprogramms [Geometrie] - Dreieck - Pyramide - Quader im Raum können einfache, planflächige Gebilde im Raum numerisch, wie auch grafisch analysiert werden.

Die Stereometrie (Raumgeometrie oder 3D Geometrie) ist ein Teilgebiet der Geometrie in dem dreidimensionale Grundformen analysiert werden. Die Geometrie im Raum behandelt maßgeblich geometrische Objekte im dreidimensionalen Raum hinsichtlich derer geometrischer Eigenschaften.
In diesem Modul stehen folgende Objekte (Gebilde) zur Verfügung, mit welchen Untersuchungen durchgeführt werden können:
- Strecke im Raum
- Dreieck im Raum
- Pyramide im Raum
- Würfel (Hexaeder) im Raum
- Quader im Raum
Beschreibung und Definition einiger Körper
Quader: Der Quader ist ein Gebilde, welcher aus drei Paaren kongruenter Rechtecke gebildet ist. Er besitzt 6 rechteckige Seitenflächen, welche rechtwinklig aufeinander stehen, 8 Ecken sowie 12 Kanten, von welchen jeweils vier die gleiche Länge besitzen und parallel zueinander liegen. Sein Volumen errechnet sich durch die Multiplikation seiner Länge, Breite und Höhe.
Würfel: Der Würfel (Hexaeder oder Kubus) ist ein Sonderfall des Quaders. Er besitzt acht rechtwinklige Körperecken, besteht aus 12 Kanten gleicher Länge und wird von sechs kongruenten Quadraten begrenzt.
Fachbegriffe
Im folgenden sind Erläuterungen zu einigen Begriffen zu diesem Fachthema aufgeführt.
Gerade quadratische Pyramide: Mit dem Begriff gerade quadratische Pyramide wird ein Körper beschrieben, dessen Mantelfläche sich aus vier gleichschenkligen, kongruenten Dreiecken zusammensetzt und dessen Grundfläche aus einem Quadrat besteht.
Quadratische Säule: Eine quadratische Säule ist ein Quader, dessen Grundfläche ein Quadrat ist.
Gerade Pyramide: Von einer geraden Pyramide wird gesprochen, wenn all ihre Seitenkanten eine einheitliche Länge besitzen.
Schiefe Pyramide: Als schiefe Pyramide wird eine Pyramide bezeichnet, deren Spitze sich nicht über dem Mittelpunkt ihrer Grundfläche befindet.
Rechteckige Pyramide: Eine rechteckige Pyramide ist ein Körper der sich aus fünf Einzelflächen zusammensetzt und dessen Grundfläche ein Rechteck bildet. Ihre vier Seitenflächen bestehen aus gleichschenkligen Dreiecken. Gegenüberliegende Dreieck sind gleich groß.
Grundflächen: Eine Grundfläche wird in zeichnerischen Darstellungen oder bei dreidimensionalen Gebilden als die unten liegende (meist ebene) Fläche betrachtet. Es handelt sich um die Fläche, auf der ein Körper positioniert ist.
Quadratische Grundfläche: Als quadratische Grundfläche wird die Grundfläche einer Pyramide bezeichnet, deren vier Kanten die selbe Länge besitzen und deren gegenüberliegende Kanten parallel zueinander verlaufen. Ihre vier Seitenflächen bestehen aus vier gleich großen kongruenten gleichschenkeligen Dreiecken.
Deckflächen: Mit dem Begriff Deckfläche wird diejenige Fläche bezeichnet, die einen Körper nach oben hin abschließt. Sie ist die Fläche, die gesehen werden kann, wenn der Körper von oben betrachtet wird.
Grundkante: Als Grundkanten einer geometrischen Figur werden die Kanten einer Grundfläche bezeichnet.
Seitenkante: Als Seitenkanten einer geometrischen Figur werden die Kanten bezeichnet, die eine Seitenfläche begrenzen.
Seitenfläche: Als Seitenflächen werden die Flächen bezeichnet, die einen geometrischen Körper seitlich begrenzen. Eine Seitenfläche ist ein abgegrenzter Teil der Oberfläche eines derartigen Gebildes.
Raumdiagonalen: Bei einer Raumdiagonale handelt es sich um eine Linie, die in einem Körper zwei einander räumlich gegenüberliegende Punkte verbindet, die nicht zur gleichen Seitenfläche gehören. Sie verbindet jeden Eckpunkt der Grundfläche eines Quaders (Würfels) mit dem am von ihm weitest entfernten Eckpunkt der Deckfläche.
Kantenlängen: Als Kantenlänge wird die Länge der Seitenkante des Quaders bezeichnet. Bei einem Objekt dieser Art bezieht sich diese Angabe auf dessen Länge a, dessen Breite b und dessen Höhe c.
Oberflächeninhalt: Der Oberflächeninhalt einer geometrischen Figur ist der gesamte Flächenhalt, den diese Figur besitzt. Es ist dies der gesamte Flächeninhalt aller äußeren Flächen dieser.
Grundseiten: Als Grundseite wird eine Seite eines Dreiecks oder gewisser Vierecke bezeichnet. Bei einem gleichschenkligen Dreieck wird als Grundseite diejenige Seite angegeben, an welcher die beiden gleichen Winkel anliegen.
Mantelfläche: Als Mantelfläche (Mantel) wird in der Geometrie ein Teil der Oberfläche bestimmter Körper bezeichnet.
Flächendiagonalen: Die Oberfläche eines Würfels (Quaders) setzt sich aus sechs Rechtecken (Quadraten) zusammen. Mit dem Begriff Flächendiagonale wird die Diagonale des Quadrats eines Würfels oder des Rechtecks eines Quaders bezeichnet.
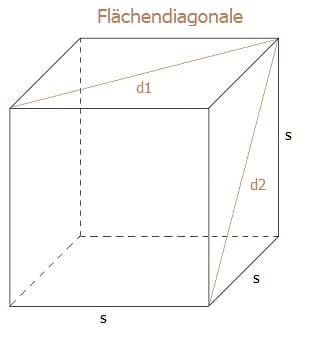
Die Diagonalen aller sechs Seitenflächen eines Würfels besitzen die gleiche Länge. Die Länge der Flächendiagonale dn eines Würfels beträgt: dn = s·√2 . Mit s: Seitenkante eines Würfels.
Oberflächenberechnung: Die Oberflächenberechnung einer dreidimensionalen Figur umfasst die Berechnung der gesamten Oberfläche (aller Teilflächen) des entsprechenden geometrischen Körpers.
Volumenberechnung: Die Volumenberechnung einer dreidimensionalen Figur umfasst die Berechnung des gesamten Volumens des entsprechenden geometrischen Körpers.
Ecken - Eckpunkte: Bei einer Ecke (einem Eckpunkt) handelt es sich bei einem dreidimensionalen Gebilde um einen Punkt in dem mehrere Kanten aneinanderstoßen.
Formeln - Formelsammlung - Formelübersicht
Nachfolgend aufgeführt sind relevante Formeln, welche zur Berechnung der Werte entsprechender Größen eines Körpers benötigt werden.
Umfang: u = 2·a + 2·b
Grundfläche: AG = a·b
Mantelfläche: AM = 2·a·c + 2·b·c
Oberfläche: AO = 2·a·c + 2·b·c + 2·a·b
Volumen (Volumen eines Quaders): V = a·b·c
Flächendiagonale: dab = √ a² + b²
Flächendiagonale: dbc = √ b² + c²
Flächendiagonale: dac = √ a² + c²
Raumdiagonale: e = √ a² + b²+ c²
Gesamtlänge aller Seiten: l = 4·a+4·b+4·c
Mit:
a,b,c: Seiten bzw. Länge, Breite und Höhe
Würfel:
Umfang: u = 4·a
Grundfläche: AG = a²
Mantelfläche: AM = 4·a²
Oberfläche: AO = 6·a²
Volumen: V = a³
Flächendiagonale: d = a·√ 2
Raumdiagonale: d = a·√ 3
Gesamtlänge aller Seiten: l = 12·a
Mit:
a: Länge einer Seite bzw. Länge, Breite und Höhe
Gerade quadratische Pyramide:
Höhe: ha = √ h² + (a/2)³
Diagonale: d = a·√ 2
Seitenkante: s = √ h² + (d/2)²
Umfang Grundfläche: u = 4·a
Grundfläche: G = a²
Mantelfläche: AM = 2·a·ha
Oberfläche: O = a² + 2·a·ha
Volumen: V = 1/3·a²·h
Neigung der Seitenfläche: α = arctan( ha/2)
Neigung der Seitenkante: β = arctan( 2·h/d)
Flächeninhalt einer Seitenfläche: As = 1/2·a·ha
Mit:
a: Länge einer Grundseite
h: Höhe der Pyramide
Euklidischer Abstand - Euklidische Distanz:
Der euklidische Abstand (die euklidische Distanz) zweier Punkte ist die gemessene Länge einer Strecke, die zwei Punkte in der Ebene oder im Raum miteinander verbindet. Bei der Verwendung kartesischer Koordinaten kann dieser Abstand mit Hilfe des Satzes von Pythagoras berechnet werden. Es gilt:
Der Abstand zweier Punkte P1(x1;y1;z1) und P2(x2;y2;z2) im Raum beträgt: dP1P2 = √ (x2 - x1)² + (y2 - y1)²+ (z2 - z1)²
Die Euklidische Distanz wird auch mit den Begriffen Abstand zwischen zwei Punkten, Entfernung zwischen zwei Punkten, Entfernung zweier Punkte oder Abstand zweier Punkte im Raum bezeichnet. Auch der Begriff Streckenlänge kommt in diesem Zusammenhang zum Einsatz.
Fläche eines Dreiecks im Raum:
Die Fläche eines Dreiecks mit den Koordinaten P1(x1|y1|z1), P1(x2|y2|z2) und P3(x3|y3|z3) beträgt:
A = √ A1² + A2²+ A3²
mit:
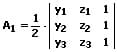
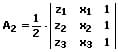
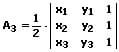
Körpernetz - Quadernetz - Würfelnetz - Pyramidennetz
1. Körpernetze: Unter dem Begriff Körpernetz wird die aufgeklappte Oberfläche eines geometrischen Körpers verstanden. Besondere Körpernetze sind das Würfelnetz, das Quadernetz sowie das Pyramidennetz.
2. Würfelnetze: Ein Würfelnetz ist das geometrische Netz eines Würfels. Es besteht aus sechs kongruenten, zusammenhängenden Quadraten, welche sich zu einem Würfel zusammenfalten lassen.

Abbildung 1 - Würfelnetz
Sechs dieser Würfelnetze besitzen die gleiche Grundstruktur. In ihrer Mitte befinden sich jeweils vier übereinander positionierte Flächen und an ihren Seiten ist jeweils eine zusätzliche Fläche angeordnet.
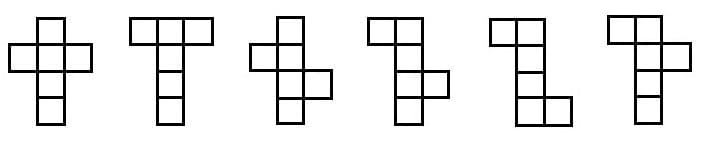
Abbildung 2 - Würfelnetz - Grundstruktur
3. Quadernetze: Ein Quadernetz besteht ebenso aus sechs kongruenten, zusammenhängenden Quadranten. Diese lassen sich zu einem Würfel zusammenfalten.
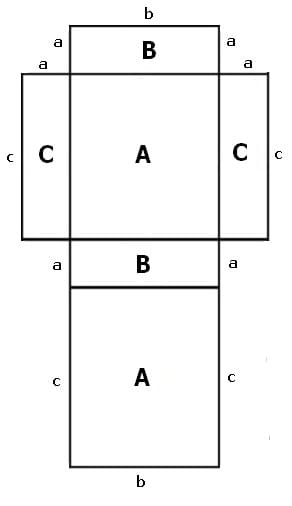
Abbildung 3 - Quadernetz
4. Pyramidennetze: Das Pyramidennetz einer vierseitigen regelmäßigen Pyramide bildet sich aus vier gleichseitigen Dreiecken sowie einem Quadrat. Durch das Zusammenfalten der Dreiecke, in Richtung des Schnittpunkts der Diagonalen des Quadrats bildet sich eine derartige Pyramide.
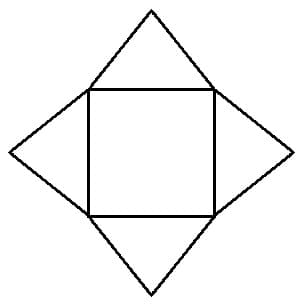
Abbildung 4 - Pyramidennetz
Screenshots

Grafische Darstellung - Beispiel 1 - Dreieck

Grafische Darstellung - Beispiel 2 - Pyramide

Grafische Darstellung - Beispiel 3 - Quader

Grafische Darstellung - Beispiel 4 - Würfel
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Berechnung und Darstellung

Untersuchen und darstellen lassen können Sie sich zuvor beschriebene Gebilde im Raum, wenn Sie wie nachfolgend geschildert vorgehen:
- Wählen Sie durch die Aktivierung des entsprechenden Kontrollschalters (Strecke, Dreieck, Pyramide ...) das Gebilde mit dem Berechnungen durchgeführt werden sollen.
- Geben Sie die erforderlichen Werte der Größen bzw. Punktkoordinaten in die dafür vorgesehenen Felder ein. Bedienen Sie ggf. zuvor die Taste Löschen.
- Bedienen Sie die Schaltfläche Berechnen.
- Möchten Sie sich das durch die Eingabewerte definierte Gebilde grafisch ausgeben lassen, so bedienen Sie die Schaltfläche Darstellen.
Sollen die Ergebnisse einer durchgeführten Berechnung bei der Darstellung ausgegeben werden, so aktivieren Sie zuvor das Kontrollkästchen Textausgabe auf dem Hauptformular des Unterprogramms. Wird das Kontrollkästchen Beschriftung aktiviert, so erfolgt die Beschriftung relevanter Raumpunkte des Gebildes bei dessen grafischer Ausgabe. Bei grafischer Ausgabe eines Dreiecks besteht darüber hinaus die Möglichkeit den Schwerpunkt dessen, durch eine Aktivierung des Kontrollkästchens Schwerpunkt, darstellen zu lassen.
Um die Kanten eines Gebildes als Rohre darstellen zu lassen, aktivieren Sie das Kontrollkästchen Kanten als Rohre.
Hinweise zur Durchführung von Berechnungen
Nachfolgend aufgeführt finden Sie die zur Durchführung numerischer Berechnungen benötigten Eingabewerte, sowie die vom Programm numerisch ermittelten Ergebnisse.
Strecke
Erforderliche Eingaben:
- Ortskoordinaten der Punkte A und B, durch welche die Strecke bestimmt wird
Folgende Werte werden nach der Definition der Strecke ermittelt und ausgegeben:
- Länge der Strecke (Streckenlänge AB)
- Richtungswinkel α, β, γ der Strecke
- Streckenmittelpunkt
Dreieck
Erforderliche Eingaben:
- Ortskoordinaten der Punkte A, B und C, durch welche das Dreieck bestimmt wird
Folgende Werte werden nach der Definition des Dreiecks ermittelt und ausgegeben:
- Innenwinkel α, β, γ des Dreiecks
- Länge der Ortsvektoren zu den Punkten A, B und C
- Normalenvektor der Ebene durch die Punkte A, B und C
- Normalenvektoren zu den Ebenen, die durch zwei Dreieckspunkte und dem Koordinatenurprung (0/0/0) gebildet werden (0AB, 0AC, 0BC)
- Flächeninhalt des Dreiecks
- Schwerpunkt des Dreiecks
- Längen der Strecken AB, AC, und BC
- Richtungswinkel α, β, γ der Strecken AB, AC, und BC
- Mittelpunkte der Strecken AB, AC, und BC
- Umfang u des Dreiecks
- Inkreisradius ri und Umkreisradius ru des Dreiecks
Pyramide
Erforderliche Eingaben:
- Ortskoordinaten der Punkte A, B, C und D, durch welche die Pyramide bestimmt wird
Folgende Werte werden nach der Definition der Pyramide ermittelt und ausgegeben:
- Höhen auf den Flächen ABC, ABD, ACD und BCD
- Richtungswinkel (Innenwinkel) α, β, γ der Strecken AB, AC, BC, AD, BD und CD
- Inhalt der Flächen ABC, ABD, ACD und BCD
- Längen der Strecken AB, AC, BC, AD, BD und CD
- Mittelpunkte der Strecken AB, AC, BC, AD, BD und CD
- Volumen der Pyramide
Würfel (Hexader)
Erforderliche Eingaben:
- Mittelpunkt des Würfels
- Seitenlängen des Würfels
Folgende Werte werden nach der Definition des Würfels ermittelt und ausgegeben:
- Volumen des Würfels
- Flächeninhalt des Würfels
- Diagonalenlänge des Würfels
Quader
Erforderliche Eingaben:
- Mittelpunkt des Quaders
- Seitenlängen a, b und c des Quaders
Folgende Werte werden nach der Definition des Quaders ermittelt und ausgegeben:
- Volumen des Quaders (Quadervolumen)
- Flächeninhalt des Quaders
- Diagonalenlänge des Quaders
Allgemein
Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.
Weitere Themenbereiche
Eben- und krummflächig begrenzte Körper
Beispiele - Aufgaben
Beispiel 1 - Berechnung einer Strecke:
Eine Strecke im Raum sei durch die Punkte A (-1 / -1 / -2) und B (0 / -1 / 3) eindeutig bestimmt.
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach der Aktivierung des Kontrollschalters Strecke, der Eingabe der Koordinatenwerte der Punkte in die hierfür vorgesehenen Felder und der Bedienung der Schaltfläche Berechnen, ermittelt das Programm:
Länge der Strecke AB (Abstand Punkt-Punkt): 5,099
Richtungswinkel α: 101,31°
Richtungswinkel β: 90°
Richtungswinkel γ: 168,69°
Streckenmittelpunkt: SM (-0,5 / -1 / 0,5)
Beispiel 2 - Berechnung eines Dreiecks:
Die Eckpunkte eines Dreieck im Raum seien gegeben mit A (-1 / 2 / 4), B (2 / -4 / 3) und C (3 / -1 / 1).
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach einer Aktivierung des Kontrollschalters Dreieck, der Eingabe der Koordinatenwerte der Punkte in die hierfür vorgesehenen Felder und einer Bedienung der Schaltfläche Berechnen, gibt das Programm aus:
Innenwinkel des Dreiecks α = 33,4423°
Innenwinkel des Dreiecks β = 59,1847°
Innenwinkel des Dreiecks γ = 87,3729°
Länge des Ortsvektors nach A: 4,5826 LE
Länge des Ortsvektors nach B: 5,3852 LE
Länge des Ortsvektors nach C: 3,3166 LE
Normalenvektor n zu Fläche ABC: (15 | 5 | 15)
Normalenvektor n zu Fläche OAB: (22 | 11 | 0)
Normalenvektor n zu Fläche OAC: (6 | 13| -5)
Normalenvektor n zu Fläche OBC: (-1 | 7 | 10)
Flächeninhalt des Dreiecks: A = 10,897 FE
Schwerpunkt des Dreiecks: S (1,333 / -1 / 2,667)
Länge der Strecke (Dreiecksseite) AB: 6,782 LE
Länge der Strecke (Dreiecksseite) AC: 5,831 LE
Länge der Strecke (Dreiecksseite) BC: 3,741 LE
Richtungswinkel α der Strecke AB: 116,252°
Richtungswinkel β der Strecke AB: 27,791°
Richtungswinkel γ der Strecke AB: 181,521°
Richtungswinkel α der Strecke AC: 133,313°
Richtungswinkel β der Strecke AC: 59,036°
Richtungswinkel γ der Strecke AC: 59,036°
Richtungswinkel α der Strecke BC: 105,501°
Richtungswinkel β der Strecke BC: 143,3°
Richtungswinkel γ der Strecke BC: 57,688°
Mittelpunkt der Strecke AB: MP1 (0,5 / -1 / 3,5)
Mittelpunkt der Strecke AC: MP2 (1 / 0,5 / 2,5)
Mittelpunkt der Strecke BC: MP3 (2 / -2,5 / 2)
Umfang des Dreiecks U: 16,354
Radius des Inkreises des Dreiecks ri: 1,332
Radius des Umkreises des Dreiecks ru: 3,394
Beispiel 3 - Berechnung einer Pyramide:
Eine Pyramide im Raum sei durch die Punkte A (1 / 2 / 2), B (-4 / -3 / -5), C (2 / 1 / -1) und D (1 / -4 / 3) definiert. Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach einer Aktivierung des Kontrollschalters Pyramide, der Eingabe der Koordinatenwerte der Punkte in die hierfür vorgesehenen Felder und der Bedienung der Schaltfläche Berechnen, gibt das Programm folgende Berechnungsergebnisse aus:
Pyramidenhöhe auf Fläche ABC: 5,578 LE
Pyramidenhöhe auf Fläche ABD: 2,536 LE
Pyramidenhöhe auf Fläche ACD: 7,117 LE
Pyramidenhöhe auf Fläche BCD: 2,704 LE
Richtungswinkel α der Strecke AB: 59,833°
Richtungswinkel β der Strecke AB: 59,833°
Richtungswinkel γ der Strecke AB: 45,289°
Richtungswinkel α der Strecke AC: 107,548°
Richtungswinkel β der Strecke AC: 72,451°
Richtungswinkel γ der Strecke AC: 25,239°
Richtungswinkel α der Strecke BC: 136,686°
Richtungswinkel β der Strecke BC: 119,017°
Richtungswinkel γ der Strecke BC: 119,017°
Richtungswinkel α der Strecke AD: 90°
Richtungswinkel β der Strecke AD: 170,538°
Richtungswinkel γ der Strecke AD: 80,538°
Richtungswinkel α der Strecke BD: 58,194°
Richtungswinkel β der Strecke BD: 96,051°
Richtungswinkel γ der Strecke BD: 32,513°
Richtungswinkel α der Strecke CD: 98,876°
Richtungswinkel β der Strecke CD: 140,49°
Richtungswinkel γ der Strecke CD: 51,887°
Fläche ABC: 12,728 FE
Fläche ABD: 27,991 FE
Fläche ACD: 9,975FE
Fläche BCD: 26,249 FE
Länge der Strecke (Seitenlänge) AB: 9,95 LE
Länge der Strecke (Seitenlänge) AC: 3,317 LE
Länge der Strecke (Seitenlänge) BC: 8,246 LE
Länge der Strecke (Seitenlänge) AD: 6,083 LE
Länge der Strecke (Seitenlänge) BD: 9,487 LE
Länge der Strecke (Seitenlänge) CD: 6,481 LE
Mittelpunkt der Strecke AB: MP1 (-1,5 / -0,5 / -1,5)
Mittelpunkt der Strecke AC: MP2 (1,5 / 1,5 / 0,5)
Mittelpunkt der Strecke BC: MP3 (-1 / -1 / -3)
Mittelpunkt der Strecke AD: MP4 (1 / -1 / 2,5)
Mittelpunkt der Strecke BD: MP5 (-1,5 / -3,5 / -1)
Mittelpunkt der Strecke CD: MP6 (1,5 / -1,5 / 1)
Volumen der Pyramide V: 23,667 VE
Beispiel 4 - Berechnung eines Würfels (Hexaeders):
Nach der Definition eines Würfels im Raum, mit:
Seitenlängen des Würfels: a = 3
Mittelpunkt des Würfels: MP (2 / -1 / -1)
(Mittelpunkt = Diagonalenschnittpunkt)
erhalten Sie nach Aktivierung des Kontrollschalters Würfel und der Bedienung der Schaltfläche Berechnen folgende Werte für den Würfel:
Volumen: V = 27 VE
Flächeninhalt: A = 54 FE
Diagonalenlänge (Raumdigonalen): d = 5,196 LE
Dessen Eckpunkte besitzen die Koordinatenwerte:
E1 (0,5 / -2,5 / -2,5)
E2 (3,5 / -2,5 / -2,5)
E3 (0,5 / 0,5 / -2,5)
E4 (0,5 / -2,5 / 0,5)
E5 (3,5 / 0,5 / -2,5)
E6 (0,5 / 0,5 / 0,5)
E7 (3,5 / -2,5 / 0,5)
E8 (3,5 / 0,5 / 0,5)
Beispiel 5 - Berechnung eines Quaders:
Nach der Definition eines Quaders im Raum, mit:
Seitenlängen des Quaders: a = 3; b = 4; c = 1;
Mittelpunkt des Quaders: MP (-1 / 1 / -2)
(Mittelpunkt = Diagonalenschnittpunkt)
erhalten Sie nach einer Aktivierung des Kontrollschalters Quader und der Bedienung der Schaltfläche Berechnen folgende Werte für den Quader:
Quadervolumen: V = 12 VE
Flächeninhalt: A = 38 FE
Diagonalenlänge: d = 5,099 LE
Dessen Eckpunkte besitzen die Koordinatenwerte:
E1 (-2,5 / -1 / -2,5)
E2 (0,5 / -1 / -2,5)
E3 (-2,5 / 3 / -2,5)
E4 (-2,5 / -1 / -1,5)
E5 (0,5 / 3 / -3,5)
E6 (-2,5 / 3 / -1,5)
E7 (0,5 / -1 / -1,5)
E8 (0,5 / 3 / -1,5)

Grafische Darstellung - Beispiel 5 - Dreieck

Grafische Darstellung - Beispiel 6 - Dreieck

Grafische Darstellung - Beispiel 7 - Pyramide

Grafische Darstellung - Beispiel 8 - Pyramide

Grafische Darstellung - Beispiel 9 - Würfel

Grafische Darstellung - Beispiel 10 - Würfel

Grafische Darstellung - Beispiel 11 - Quader

Grafische Darstellung - Beispiel 12 - Quader
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Pyramide
Wikipedia - Quader
Wikipedia - Würfel
Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
Startfenster des Unterprogramms Dreieck, Pyramide und Quader im Raum
MathProf 5.0 - Startfenster des Unterprogramms Krummflächig begrenzte Körper

MathProf 5.0 - Grafikfenster des Unterprogramms Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















