MathProf - Fourier-Reihe - Fourier-Analyse - Fourier-Koeffizienten

Modul Fourierreihen

---

Das Unterprogramm [Analysis] - [Reihen] - Fourier-Reihen bietet die Möglichkeit, Untersuchungen zum Fachthema Fourier-Reihen durchzuführen und die Koeffizienten der Fourier-Reihen ermitteln zu lassen.

 

 
Als Fourierreihe (Fourier-Reihe) wird eine Reihe bezeichnet, mit Hilfe derer eine periodische, abschnittsweise stetig definierte Funktion in Form einer Reihe aus Sinusfunktionen und Cosinusfunktionen dargestellt wird. Eine Reihe dieser Art wird auch als Funktionenreihe (Funktionenfolge) bezeichnet. Die Bildung derartiger Reihen wird Fourierreihenentwicklung genannt. Die Entwicklung einer derartigen Reihe erfolgt nach aufsteigenden Frequenzen.
 
In manchen naturwissenschaftlich-technischen Anwendungsgebieten (z.B. Elektrotechnik) treten Zusammenhänge auf, bei welchen es erforderlich ist, diese mit Hilfe der Überlagerung sinusförmiger Funktionen zu beschreiben. Mittels der Durchführung einer Fourier-Analyse ist es möglich, die Koeffizienten der trigonometrischen Funktionen Sinus und Cosinus so zu bestimmen, dass diese durch Überlagerung eine beliebige Funktion beschreiben können. Funktionen dieser Art werden als Fourierreihen bezeichnet. Diese Koeffizienten heißen Fourier-Koeffizienten (Fourierkoeffizienten).
 
Dieses Modul ermöglicht es, Fourier-Reihen mit einer Periode von p = 2π von stetigen Funktionen entwickeln und die reellen Koeffizienten a_n und b_n, sowie die komplexen Koeffizienten c_n bzw. c_-n bestimmen zu lassen.
 

 
Eine periodische Funktion kann in Form einer trigonometrischen Fourierreihe und somit als eine Summe harmonischer Schwingungen dargestellt werden. Neben der Grundfrequenz besitzt eine Reihe dieser Art ausschließlich Frequenzen die ganzzahlige Vielfache dieser sind.

Ist f(x) eine eindeutige, im Intervall [0,2π] stückweise monotone und differenzierbare periodische Funktion mit der Periode 2π, so lässt sich diese in eine Fourierreihe von f(x) entwickeln. Fourierreihen können in der reellen Form sowie in der komplexen Form beschrieben werden. Auf diese beiden Darstellungsformen wird nachfolgend eingegangen.

 
1. Reelle Form:

Ein nicht-sinusförmiger Schwingungsvorgang y = y(t) mit einer Kreisfrequenz ω₀ kann, wie folgt, nach Fourier in seine harmonischen Komponenten (Grundschwingung und Oberschwingung) zerlegt werden:
 

 
Die reellen Koeffizienten dieser Zerlegung tragen die Bezeichnungen a₀, a₁, a₂ ... und b₁, b₂ ...bzw. a_k und _bk und werden als Fourier-Koeffizienten (Fourierkoeffizienten) bezeichnet. Sie werden aus nachfolgend aufgeführten Integralen berechnet:
 

 
2. Komplexe Form:

 

Fourier-Reihen können zudem mit Hilfe komplexer Zahlen beschrieben werden:
 

 

Eine Einsicht darüber erlangt man, indem man die Summe aufteilt:
 

 

 

Durch Koeffizientenvergleich erhält man:
 

 

 

 
Es gilt:
 

 

mit:

 
T = 2π/ω₀: Schwingungsdauer

ω₀: Kreisfrequenz der Grundschwingung

nω₀: Kreisfrequenzen der harmonischen Oberschwingungen (n = 2,3,4...)

a_n,b_n: Reelle Koeffizienten

c_n: Komplexe Koeffizienten
n ∈ N

---

Gleichanteil (Gleichwert):

Das Konstantenglied a₀ einer Fourier-Reihe wird der Gleichanteil (Gleichwert) der Funktion f(t) genannt.

Grundschwingung - Oberschwingung:

Besitzt der Parameter n einer Reihe den Wert 1, so wird von der Grundschwingung des Systems gesprochen und ω₀ = 2πf = 2πf/T ist die Kreisfrequenz dieser. Ist dieser ganzzahlige Wert des Parameters größer 1 (n > 1), so werden die hierbei entstehenden Wellen als Oberschwingungen dessen mit einer Kreisfrequenz von ω_n = n2πf = n2πf/T bezeichnet (z.B. sin(2x) und cos(2x), sin(3x) und cos(3x)).
 

 

 
Gehen Sie wie nachfolgend beschrieben vor, um Koeffizienten von Fourier-Reihen bestimmen zu lassen und sich Zusammenhänge zu diesem Fachthema grafisch zu veranschaulichen.
 

1. Definieren Sie die zu analysierende Funktion, gemäß den geltenden Syntaxregeln, im Eingabefeld f(x,p) =.
    
2. Legen Sie die zur Ermittlung der Reihe zu verwendende Koeffizientenanzahl durch die Eingabe eines ganzzahligen Werts in das Feld Anz. Koeffizienten fest.
    
3. Nach einer Bedienung der Schaltfläche Berechnen gibt das Programm die Werte für die entsprechenden rellen Koeffizienten a[n] sowie b[n] aus. Zudem werden die Werte der komplexen Koeffizienten c[n] bzw. c[-n] in der Tabelle angezeigt.
    

4. Um sich die Darstellung der ermittelten Reihe grafisch ausgeben zu lassen, legen Sie in den Eingabefeldern (Darstellungsbereich von x1 = und bis x2 =) den zur Ausgabe der entsprechenden Kurve zu verwendenden Wertebereich fest (voreingestellt: -π ≤ x ≤ π). Standardwerte hierfür können Sie holen, indem Sie das entsprechende Eingabefeld fokussieren und die rechte Maustaste bedienen.
    

   Beachten Sie: Der gewählte Darstellungsbereich (Periode p) darf den Wert p = 2π nicht überschreiten. Bei der Bemessung dieses Bereichs gilt: |x2-x1| ≤ 2π.
    

5. Bedienen Sie hierauf die Schaltfläche Darstellen.
    

6. Das Programm verwendet nach Aufruf der grafischen Darstellung für die Anzahl von Gliedern den im Eingabefeld Koeffizientenanzahl festgelegten Wert. Durch eine Bedienung des Rollbalkens Koeffizientenanzahl kann dieser hierauf verändert werden.
    

7. Durch die Auswahl des entsprechenden Eintrags aus der aufklappbaren Box bestehen folgende Möglichkeiten die Darstellung zu beeinflussen. Es sind dies:

    

   Reihe in gew. Bereich und Fkt.: Darstellung der ermittelten Reihe über den gewählten Ausgabebereich (x1 ≤ x ≤ x2) sowie Darstellung der Funktion f(x,p).
   Reihe in gew. Bereich ohne Fkt.: Darstellung der ermittelten Reihe über den gewählten Ausgabebereich (x1 ≤ x ≤ x2).
   Reihe über ges. Bereich und Fkt.: Darstellung der ermittelten Reihe über den gesamten Darstellungsbereich (Werte in Eingabefeldern für festgelegten Darstellungsbereich werden ignoriert) sowie Darstellung der Funktion f(x,p).
   Reihe über ges. Bereich ohne Fkt.: Darstellung der ermittelten Reihe über den gesamten Darstellungsbereich (Werte in Eingabefeldern für festgelegten Darstellungsbereich werden ignoriert).
    

8. Durch die Aktivierung des Kontrollkästchens Bereich legen Sie fest, ob der eingestellte Darstellungsbereich markiert werden soll.
    
9. Um sich den Ordinatenwert der Funktion, bzw. den entsprechenden Wert für die ermittelte Fourier-Reihe bei einer bestimmten Abszissenposition ausgeben zu lassen, aktivieren Sie das Kontrollkästchen Punkt, positionieren Sie den Mauscursor bei der gewünschten Abszissenposition, oder bedienen die Schaltfläche Punkt.
    
10. Enthält der Funktionsterm das Einzelzeichen P, so legen Sie, wie unter Verwendung von Funktionsparametern beschrieben, nach einer Bedienung des Schalters Parameter P den zu durchlaufenden Wertebereich für diesen Funktionsparameter, sowie die zu verwendende Schrittweite, fest. Positionieren Sie hierauf den Schieberegler Parameter P, um den Einfluss des Parameters P zu untersuchen.
     
11. Möchten Sie Analysen mit Hilfe von Simulationen durchführen, so wählen Sie durch Aktivierung des Kontrollschalters Koeffizientenanzahl oder Parameter P die Art der Simulation die Sie durchführen lassen möchten. Um Koeffizientenanzahlen simulativ verändern, oder eine automatisch ablaufende Parameterwertsimulation durchführen zu lassen, klicken Sie auf die Schaltfläche Simulation.
    
    Vor Ausführung einer Koeffizientenanzahlsimulation wird Ihnen ein Formular zur Verfügung gestellt. Zudem können Sie den für die Schrittweite zu verwendenden Wert einstellen. Ändern Sie diesen bei Bedarf und bestätigen Sie mit OK. Beendet werden kann die Ausführung einer Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

Hinweise:

Es erfolgt keine Überprüfung der Funktion auf Unstetigkeitsstellen. Verwenden Sie deshalb ausschließlich Funktionen, die innerhalb des gewählten Bereichs stetig sind - andernfalls erhalten Sie eine fehlerhafte Darstellung bzw. fehlerhaft ermittelte Koeffizientenwerte.

 

In diesem Unterprogramm kann eine numerische Analyse mit einer Koeffizientenanzahl durchgeführt werden die zwischen 1 und 50 liegt. Je höher diese gewählt wird, desto genauer sind die Berechnungsergebnisse.

 

Beim Aufruf einer grafischen Darstellung wird die Liste evtl. zuvor ausgegebener Berechnungsergebnisse nicht aktualisiert! Dies ist stets separat durch eine Bedienung der Schaltfläche Berechnen durchzuführen!
 
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

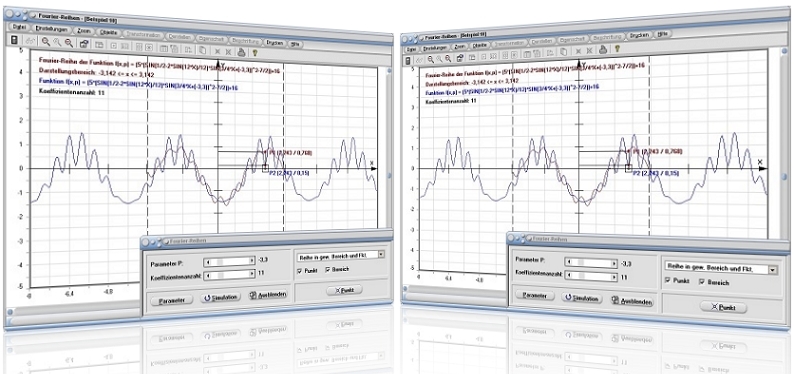
Wurde zur Analyse der Zusammenhänge ein Funktionsterm erstellt, der kein Einzelzeichen P zur Definition eines Funktionsparameters enthält, so wird bei der Ausgabe einer grafischen Darstellung nachfolgend gezeigtes Bedienformular zur Verfügung gestellt.

 

 

Wurde zur Analyse der Zusammenhänge ein Funktionsterm erstellt, der das Einzelzeichen P zur Definition eines Funktionsparameters enthält, so wird bei der Ausgabe einer grafischen Darstellung das nachfolgend abgebildete Formular eingeblendet.

 

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Fourier-Summen

 

Beispiel 1:

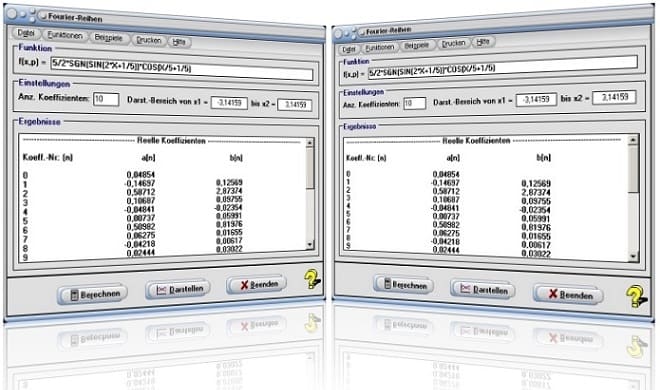
Bei Durchführung einer Fourier-Analyse mit der Funktion f(x) = -x³/50 über einen Bereich von 0 bis 2π erhalten Sie nach Eingabe des Terms -X^3/50, der Festlegung einer Koeffizientenanzahl von 5 und der Eingabe der Werte 0 und 6,28319 für den Darstellungsbereich, sowie einer Bedienung der Schaltfläche Berechnen, folgende Ergebnisse für die ermittelten reellen Koeffizienten a[0] - a[5] und b[1] - b[5] der Fourier-Reihe:
 

Koeff.-Nr. (n)	a[n]	b[n]
0	-1,23474
1	-0,74297	1,33914
2	-0,17748	0,75957
3	-0,07276	0,51749
4	-0,03611	0,39103
5	-0,01914	0,31391

 
Bei Ausgabe der grafischen Darstellung nach der Durchführung eines Klicks auf die Schaltfläche Darstellen wird ersichtlich, dass diese Reihe sich im Bereich [0;2π] der Funktion f(x) = -x³/50 nähert. Ferner kann festgestellt werden, dass diese Konvergenz bei einer Erhöhung der Koeffizientenzahl zunimmt.
 

Für die Werte der komplexen Koeffizienten c[n] und c[-n] gibt das Programm zudem aus:
 

Koeff.-Nr. (n)	c[n]	c[-n]
0	-0,61737
1	-0,371-0,669i	-0,371+0,669i
2	-0,088-0,379i	-0,088+0,379i
3	-0,036-0,258i	-0,036+0,258i
4	-0,018-0,195i	-0,018+0,195i
5	-0,009-0,156i	-0,009+0,156i

 
Beispiel 2:

Es gilt, die Fourier-Reihe der Funktion f(x) = 2·sin(x/3-cos(x)/10) ermitteln und sich grafisch darstellen zu lassen. Weiterhin sind die Koordinatenwerte der definierten Funktion, sowie der ermittelten Fourier-Reihe bei einer Koeffizientenanzahl von 8, an Stelle x = 3 auszugeben. Der Darstellungsbereich sei mit 0 bis 2π festzulegen.

 

Vorgehensweise und Lösung:

 

Der Funktionsterm 2*SIN(X/3-COS(X)/10) wird im dafür vorgesehenen Eingabefeld definiert. Im Eingabefeld Anz. Koeffizienten wird der Wert 8 festgelegt.

 

Nach einer Bedienung der Schaltfläche Darstellen und einer Positionierung des Rollbalkens Koeffizientenanzahl auf den Wert 8 (voreingestellt), sowie einer Festlegung der Koordinaten des Mausfangpunkts auf (3 / 0) nach einer Aktivierung des Kontrollkästchens Punkt und der Durchführung eines Klicks auf die Schaltfläche Punkt kann entnommen werden, dass der Ordinatenwert der Funktion an dieser Stelle y = 1,816, sowie der entsprechende Wert für die ermittelte Fourier-Reihe an dieser Stelle y = 1,782 beträgt.

 

Wird die grafische Darstellung beendet und hierauf die Schaltfläche Berechnen bedient, so gibt das Programm die Werte der reellen Koeffizienten a[n] und b[n] sowie der komplexen Koeffizienten c[n] und c[-n] für die ermittelte Fourier-Reihe aus.
 
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6


Grafische Darstellung - Beispiel 7


Grafische Darstellung - Beispiel 8
    

Nachfolgend aufgeführt sind einige besondere Fourierreihen, welche häufig Anwendung finden. In diesen Formeln ist dem Wert ω0·t die Variable x zugewiesen.

 
1. Rechteckkurve I:

2. Rechteckkurve II:

 
3. Rechteckimpuls I:

 

4. Rechteckimpuls II:
 



 
5. Trapezkurve:
 

 

 

 

6. Trapezimpuls:

  


 
7. Dreieckskurve:
 


 
8. Dreieckimpuls:
 


 

 
9. Sägezahnkurve I:

 


 
10. Sägezahnkurve II:
 


 
11. Zweiweggleichrichtung - Sinusimpuls:
 


 
12. Zweiweggleichrichtung - Cosinusimpuls:
 

 
 
13. Einweggleichrichtung - Sinusimpuls:


 
 
14. Einweggleichrichtung - Cosinusimpuls:

 

  

 

 
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Fourier-Reihe und unter Wikipedia - Trigonometrisches Polynom zu finden.
 

 

 

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

 

Startfenster des Unterprogramms Fourier-Reihen
 

MathProf 5.0 - Unterprogramm Fourier-Summen

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---