MathProf - Gebrochen rationale Funktionen - Polynomgleichung
Fachthema: Gebrochen rationale Funktionen
MathProf - Analysis - Ein Programm zum Lösen unterschiedlichster Aufgaben und zur Visualisierung relevanter Sachverhalte aus verschiedenen Teilgebieten der grundlegenden Mathematik und der höheren Mathematik mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich hierfür interessieren.
Online-Hilfe
für das Modul zur interaktiven Analyse und Darstellung gebrochenrationaler Funktionen und derer Polgeraden bei Polstellen sowie evtl. vorhandender Asymptoten.
In diesem Unterprogramm erfolgt neben dem Zeichnen des Graphen einer gebrochen rationalen Funktion die Anwendung der Polynomdivision, der Polynommultiplikation und der Substitution sowie die Durchführung einer Kurvendiskussion mit dieser.
Hierbei wird neben vielem anderen das Berechnen der Nullstellen, das Bestimmen der Extrempunkte sowie der Wendestellen der definierten Funktion durchgeführt. Auch das Plotten der 1. Ableitungsfunktion und 2. Ableitungsfunktion rationaler Funktionen wird ermöglicht.
Das Berechnen der Werte erforderlicher Größen erfolgt zur Echtzeit. Der Rechner stellt die entsprechenden Zusammenhänge unmittelbar nach Eintritt einer interaktiven Operation dar. Jedes relevante Ergebnis einer durchgeführten Berechnung zu diesem Fachthema wird aktualisiert ausgegeben.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul:Gebrochen rationale Funktion - Kurvendiskussion - Polstellen - Asymptoten - Rationale Funktion ableiten - Nullstellen einer rationalen Funktion - Polstellen einer rationalen Funktion - Asymptote bestimmen - Gebrochenrationale Funktion plotten - Funktionsgraph - Ableiten von gebrochenrationalen Funktionen - Polstellen bestimmen - Extremstellen von gebrochenrationalen Funktionen - Extremstellen - Extrempunkte von gebrochenrationalen Funktionen - Verhalten von gebrochenrationalen Funktionen - Einfache Polstellen - Gebrochen rationale Funktionen mit Parameter - Parameter - Gleichung - Ableitung - Nullstellen - Polstellen - Wendepunkte - Definition - Eigenschaften - Funktionsterm - Formel - Kurvendiskussion - Asymptoten - Graph - Plotten - Grafisch - Bild - Darstellen - Plotter - Rechner - Berechnen - Beispiel - Grafik - Plotten - Term - Zeichnen - Darstellen - Grafische Darstellung - Mehrfache Polstellen - Nullstellen von Polynomgleichungen |
Gebrochenrationale Funktionen - Interaktiv
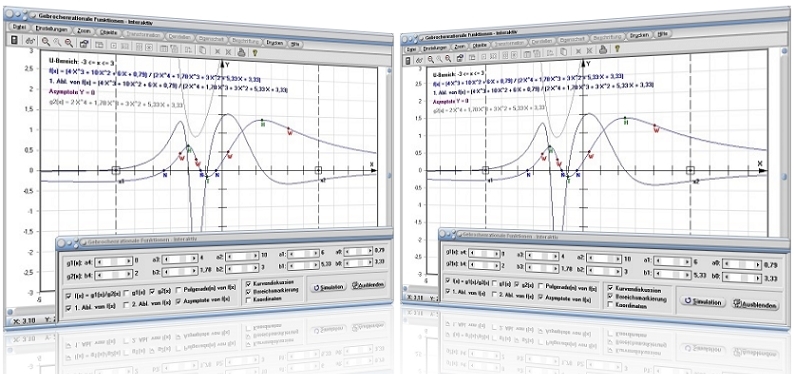
Modul Gebrochenrationale Funktionen - Interaktiv
Mit Hilfe des Unterprogramms [Analysis] - [Ganz- und gebrochenrationale Funktionen] - Gebrochenrationale Funktionen - Interaktiv können Untersuchungen mit echt gebrochenrationalen Funktionen (rationalen Funktionen) interaktiv durchgeführt werden. Hierzu zählt u.a. die Durchführung der Polynomdivision und die Ermittlung evtl. vorhandener Pole (Polstellen) und Asymptoten.
Es können Funktionen analysiert werden, die in nachfolgend aufgeführter Form vorliegen:
Es lassen sich darstellen:
- Gebrochenrationale Funktion f(x)
- Teilfunktionen g1(x) und g2(x) der Funktion f(x)
- 1. Ableitung f'(x) der Funktion f(x)
- 2. Ableitung f''(x) der Funktion f(x)
- Polgeraden (Pole) der Funktion f(x)
- Asymptote der Funktion f(x) (Senkrechte Asymptote - Waagerechte Asymptote - Hüllkurve)
Zudem werden ermittelt:
- Gleichung der Asymptote (Hüllkurve) der Funktion f(x)
- Nullstellen und Pole der Funktion f(x)
- Extremwerte (Extrempunkte) der Funktion f(x)
- Wendepunkte (Wendestellen) der Funktion f(x)
Darstellung
Gehen Sie folgendermaßen vor, um eine interaktive Analyse mit gebrochenrationalen Funktionen (gebrochen rationalen Funktionen) durchführen zu lassen:
- Bestimmen Sie durch die Aktivierung/Deaktivierung der entsprechenden Kontrollkästchen, welche der o.a. Kurven dargestellt werden soll.
- Verändern Sie durch die Positionierung der entsprechenden Schieberegler a0, a1, a2, a3, a4 bzw. b0, b1, b2, b3, b4 auf dem Bedienformular die Werte der Koeffizienten a0 - a4, bzw. b0 - b4 der gebrochenrationalen Funktion.
- Legen Sie durch die Aktivierung/Deaktivierung des Kontrollkästchens Kurvendiskussion fest, ob mit der Funktion f(x) eine Kurvendiskussion durchgeführt werden soll.
Möchten Sie den Untersuchungsbereich zur Durchführung einer Kurvendiskussion mit der Maus verändern, so aktivieren Sie das Kontrollkästchen mit der Bezeichnung Bereichsmarkierung, klicken in den rechteckig umrahmten Mausfangbereich eines Bereichsmarkierungspunkts und bewegen Sie den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts (je schmaler der Bereich gewählt wird, desto exakter sind die resultierenden Berechnungsergebnisse).
- Es besteht die Möglichkeit eine Veränderung von Koeffizientenwerten vom Programm simulieren zu lassen. Bedienen Sie hierfür die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Auswahlformular zur Verfügung gestellt, auf welchem Sie die simulativ zu verändernden Vorgabebedingungen durch die Aktivierung des entsprechenden Kontrollschalters festlegen. Bestätigen Sie mit OK. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
Bei der Durchführung einer Kurvendiskussion werden angezeigt:
-
Nullstellen der ermittelten Funktion (N: Nullstelle)
-
Extrema (Extremstellen) der ermittelten Funktion (H: Hochpunkt ; T: Tiefpunkt)
-
Wendepunkte (Wendestellen) der ermittelten Funktion (W: Wendepunkt : Wendestelle)
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformular
Es wird nachfolgend gezeigtes Bedienformular zur Verfügung gestellt, auf welchem Sie die Koeffizienten einer gebrochenrationalen Funktion bis 4. Grades festlegen können.
Hierbei können die Parameter folgender Einflussgrößen verändert werden:
-
a0 ... a4: Koeffizienten der ganzrationalen Funktion g1(x)
-
b0 ... b4: Koeffizienten der ganzrationalen Funktion g2(x)
Darstellen lassen sich durch die Aktivierung der entsprechenden Kontrollschalter:
f(x) = g1(x)/g2(x): Gebrochenrationale Funktion f(x) = g1(x)/g2(x)
g1(x): Zähler der gebrochenrationalen Funktion f(x)
g2(x): Nenner der gebrochenrationalen Funktion f(x)
1. Abl. von f(x): Erste Ableitung der gebrochenrationalen Funktion f(x)
2. Abl. von f(x): Zweite Ableitung der gebrochenrationalen Funktion f(x)
Polgerade von f(x): Polgerade der gebrochenrationalen Funktion f(x)
Asymptote von f(x): Asymptote (senkrechte Asymptote - waagerechte Asymptote) der gebrochenrationalen Funktion f(x)
Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung des entsprechenden Kontrollkästchens folgende zusätzliche Einstellung vornehmen:
- Koordinaten: Anzeige der Koordinaten der mittels Kurvendiskussion ermittelten Punkt
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Beispiel
Positionieren Sie die Rollbalken wie folgt:
| a4: 8 a3: 4 a2: 7 a1: 10 a0: -1 | b4: 6 b3: 0 b2: 3 b1: 2 b0: 3 |
Hierdurch sind die Koeffizienten für die beiden Funktionen g1(x) und g2(x) festgelegt. Die Terme lauten somit:
g1(x) = 8·x4+4·x3+7·x2+10·x-1
g2(x) = 6·x4+3·x2+2·x+3
Bei einer Aktivierung des Kontrollkästchens f(x) = g1(x)/g2(x) (voreingestellt) stellt das Programm die gebrochenrationale Funktion f(x) = g1(x)/g2(x) = (8·x4+4·x3+7·x2+10·x-1)/(6·x4+3·x2+2·x+3) dar.
Nach einer Aktivierung der Kontrollkästchen g1(x) bzw. g2(x) werden die Kurven ausgegeben, welche durch die gebrochenrationale Funktion g1(x) bzw. g2(x) beschrieben werden.
Wird das Kontrollkästchen 1.Abl. von f(x) = g1(x)/g2(x) aktiviert, so stellt das Programm die 1. Ableitung der gebrochenrationalen Funktion f(x) = g1(x)/g2(x) dar.
Die Kurve, welche durch 2. Ableitung der Funktion f(x) = g1(x)/g2(x) beschrieben wird, wird ausgegeben, wenn das Kontrollkästchens 2. Abl. aktiviert wird.
Nach einer Aktivierung des Kontrollkästchens Asymptote ermittelt das Programm die Gleichung y = 1,333 für die Asymptote der Funktion f(x) = g1(x)/g2(x) und gibt diese aus.
Wird zudem das Kontrollkästchen Kurvendiskussion aktiviert, so führt das Programm eine Kurvendiskussion mit der Funktion f(x) durch und ermittelt für den voreingestellten Untersuchungsbereich -3 ≤ x ≤ 3:
Die gebrochenrationale Funktion f(x) besitzt innerhalb des festgelegten Untersuchungsbereichs:
| Nullstellen: | N (-1 / 0) | N (0,093 / 0) | |
| Extrema: | HP (1,124 / 2,016) | TP (-0,434 / -1,397) | |
| Wendepunkte: | W (-0,758 / 0,704) | W (0,049 / -0,16) | W (1,597 / 1,913) |
Grafische Darstellung - Beispiel 1
Grafische Darstellung - Beispiel 2
Grafische Darstellung - Beispiel 3
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Rationale Funktion
Wikipedia - Kurvendiskussion
Wikipedia - Ableitung
Wikipedia - Nullstelle
Wikipedia - Extremwert
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
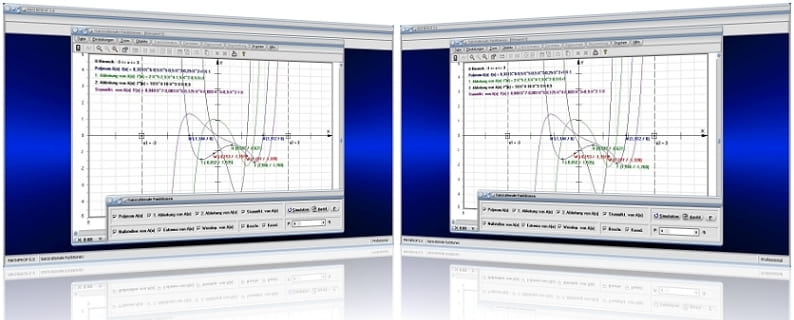
MathProf 5.0 - Unterprogramm Ganzrationale Funktionen
MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
