MathProf - Kombinatorik - Reihenfolge - Wiederholung - Kombinationen

 

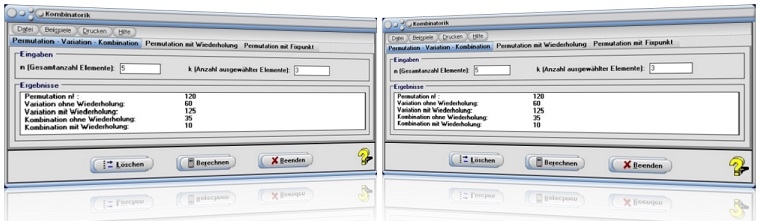
Modul Kombinatorik

---

 
Unter dem Menüpunkt [Stochastik] - Kombinatorik können Berechnungen zum mathematischen Fachthemengebiet Kombinatorik durchgeführt werden.

 

 

Die diskrete Mathematik ist ein Teilgebiet der Mathematik, welches sich mit diskreten mathematischen Fragestellungen hinsichtlich endlicher oder abzählbarer Mengen befasst. Zu diesem Fachgebiet zählen unter anderem die Kombinatorik sowie die Graphentheorie.
 
Mit Hilfe der Kombinatorik werden die verschiedenen Möglichkeiten der Anordnung von Gegenständen untersucht. Sie ist die Lehre vom Abzählen (der Abzählung) bzw. dem Zählen. Gegenstände werden als Elemente bezeichnet. Unter den kombinatorischen Abzählverfahren wird zwischen Permutation, Variation und Kombination unterschieden.

Die Aufgabe der Kombinatorik besteht unter anderem darin, die Anzahl unterschiedlicher Auswahl- bzw. Anordnungsmöglichkeiten (Kombinationsmöglichkeiten oder Variationsmöglichkeiten) zu ermitteln. Diese Anzahl bestehender Anordnungsmöglichkeiten (die Variantenzahl) wird auch als die Zahl P einer Permutation bezeichnet.

Die abzählende Kombinatorik setzt sich mit der Ermittlung der Anzahl möglicher Anordnungen auseinander. Hierbei wird zwischen unterscheidbaren Elementen und nicht unterscheidbaren Elementen differenziert. Zudem erfolgt die Berücksichtigung oder Nichtberücksichtigung der Reihenfolge der Anordnungen.

---

In diesem Programmteil können zu folgenden Teilbereichen der Kombinatorik Berechnungen durchgeführt werden:
 

• Permutation ohne Wiederholung
• Permutation mit Wiederholung
• Variation ohne Wiederholung
• Variation mit Wiederholung
• Kombination ohne Wiederholung
• Kombination mit Wiederholung
• Permutation mit Fixpunkt

 
Dieses Modul ermöglicht bei Kombinationen unter anderem das Berechnen der Anzahl von Kombinationsmöglichkeiten, bei Variationen das Berechnen der Anzahl von Variationsmöglichkeiten (Variantenzahl) sowie bei Permutationen das Berechnen der Anzahl von Permutationsmöglichkeiten.
 
Die in diesem Unterprogramm verwendeten Bezeichnungen lauten:

A: Anzahl der Möglichkeiten

n: Anzahl aller Elemente

k: Anzahl ausgewählter Elemente

 
 

 
Unter der Fakultät einer natürlichen Zahl wird das Produkt aller natürlichen Zahlen von 1 bis n verstanden. Sie errechnet sich wie folgt:

n! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ...  ⋅ (n-1)⋅n

In nachfolgend gezeigter Tafel sind die Fakultäten von 1! bis 20! aufgeführt.
 

n	n!
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000

   

 

 
Das allgemeine Zählprinzip (Produktregel der Kombinatorik) erteilt bei einem Zufallsexperiment Auskunft über die Anzahl bestehender Möglichkeiten. Gemäß dem Zählprinzip kann die Anzahl der bei einem Baumdiagramm zur Verfügung stehenden Verzweigungen einzelner Stufen durch deren Multiplikation ermittelt werden. Bei einem Zählprinzip sind alle bestehenden Möglichkeiten miteinander zu multiplizieren.

Um zu ermitteln, wie viele Möglichkeiten bestehen, aus k unterschiedlichen Mengen eine Kombination mit je einem Element aus jeder Menge zu erzeugen, werden sogenannte Tupel gebildet. Deren Anzahl kann ermittelt werden, indem die einzelnen Elemente aller k Mengen miteinander multipliziert werden. Für diese Anzahl gilt:

n = n₁· n₂ ·n₃ · .... n_k [mit n > 0 und n_k > 1]

Um beispielsweise zu berechnen, wie viele verschiedene Ausgänge bei enem Wettrennen mit 5 Teilnehmern möglich sind, ergibt das Zählprinzip den Wert 5·4·3·2·1 = 120 = 5!. Dies entspricht dem Wert der Fakultät der Zahl 5.
  

Permutationen von n Elementen sind die Anordnung aller n Elemente in jeder möglichen Reihenfolge. Prinzipiell handelt es sich hierbei darum, alle Elemente einer Ausgangsmenge in einer bestimmten Reihenfolge anzuordnen.
 

Die Voraussetzungen für eine Permutation ohne Wiederholung sind:

• alle n Elemente der Ausgangsmenge müssen sich unterscheiden
• alle n Elemente müssen ausgewählt werden
• ein Element kann nicht mehrmals ausgewählt werden

Die Formel zur Berechnung einer Permutation ohne Wiederholung lautet:


 

Die Voraussetzungen für eine Permutation mit Wiederholung sind:

• mindestens zwei Elemente einer Ausgangsmenge sind identisch, d.h. nicht alle Elemente der Ausgangsmenge unterscheiden sich voneinander
• alle n Elemente müssen ausgewählt werden
• ein Individualelement kann nicht mehrmals ausgewählt werden, ein Element mit gleicher Eigenschaft hingegen schon

Die Formel zur Berechnung einer Permutation mit Wiederholung lautet:


 

k₁...k_n : Anzahl der Elemente mit gleichen Eigenschaften (Subfakultät - Gruppen gleicher Elemente)

 
Fixpunkt einer Permutation:

Ein Element, dessen Position sich bei einer Permutation nicht ändert, nennt man Fixpunkt der Permutation. Bei der Permutation 1,2,3,4 -> 1,3,2,4 sind deshalb die Zahlen 1 und 4 Fixpunkte.

Eine Transposition (oder Transpositionierung) ist ein Zyklus (eine Permutation) der Länge 2. Sie besteht aus der Vertauschung zweier Elemente einer Permutation. Jede Permutation lässt sich auch als Produkt von Transpositionen darstellen.
 

Variationen sind Anordnungen, welche aus n gegebenen Elementen nur eine bestimmte Anzahl k in allen möglichen Reihenfolgen enthalten. Prinzipiell handelt es sich hierbei um die Vorgehensweise, einige Elemente aus einer Ausgangsmenge auszuwählen und diese zusätzlich in eine Reihenfolge zu bringen. Es wird die Anzahl möglicher Variationen aus einer Menge berechnet.

Der Unterschied zwischen einer Variante und einer Variation besteht darin, dass unter einer Variante eine bestimmte Charaktereigenschaft verstanden wird. Mit einer Variation hingegen wird die Menge der Möglichkeiten beschrieben wie die entsprechende Charaktereigenschaft belegt sein kann.

 
Die Voraussetzungen für eine Variation ohne Wiederholung sind:

• alle n Elemente der Ausgangsmenge unterscheiden sich voneinander
• es werden einige (k) Elemente aus der Ausgangsmenge ausgewählt
• ein Element kann nicht mehrmals ausgewählt werden

Die Formel zur Berechnung einer Variation ohne Wiederholung lautet:


 

Die Voraussetzungen für eine Variation mit Wiederholung sind:

• alle n Elemente der Ausgangsmenge unterscheiden sich voneinander
• es werden einige (k) Elemente aus der Ausgangsmenge ausgewählt
• ein Element kann mehrmals ausgewählt werden

Die Formel zur Berechnung einer Variation mit Wiederholung lautet:

 
 

Werden jeweils k Elemente aus der Gesamtanzahl n ausgewählt in beliebiger, jedoch nur jeweils in einer Reihenfolge angeordnet, entstehen Kombinationen. Eine Reihenfolge definiert die Ordnung bezüglich der Menge der einzelnen Elemente. Die Anzahl bestehender Kombinationsmöglichkeiten ergibt sich aus der festgelegten Anzahl durchführbarer Kombinationen.
 
Werden beispielsweise Zahlenkombinationen aus Ziffern gebildet, so bestehen, abhängig von der Anzahl der Ziffern aus denen die zu untersuchende Zahl besteht, so viele Möglichkeiten diese Ziffern anzuordnen, wie diese Zahl Stellen besitzt. Bei einer Reihenfolge von Ziffern mit 6 Stellen, existieren somit genau 1.000.000 Möglichkeiten diese Ziffern anzuordnen.
 

Die Voraussetzungen für eine Kombination ohne Wiederholung sind:
 

• alle n Elemente der Ausgangsmenge unterscheiden sich voneinander
• es werden einige (k) Elemente aus der Ausgangsmenge ausgewählt
• ein Element kann nicht mehrmals ausgewählt werden

Berechnung einer Kombination ohne Wiederholung. Die Anzahl möglicher Kombinationen (z.B. mögliche Zahlenkombinationen) beim Ziehen von k Elementen aus einer Gesamtmenge von n Elementen kann im vorliegenden Fall mit nachfolgend gezeigter Formel berechnet werden.
 

 
 

Die Voraussetzungen für eine Kombination mit Wiederholung sind:
 

• alle n Elemente der Ausgangsmenge unterscheiden sich voneinander
• es werden einige (k) Elemente aus der Ausgangsmenge ausgewählt (Abzählverfahren)
• ein Element kann mehrmals ausgewählt werden

Berechnung einer Kombination mit Wiederholung. Die Anzahl möglicher Kombinationen (z.B. mögliche Zahlenkombinationen) beim Ziehen von k Elementen aus einer Gesamtmenge von n Elementen kann beim Vorliegen dieses Sachverhalts mit nachfolgend gezeigter Formel ermittelt werden.

 
 

 
Nach der Wahl des entsprechenden Registerblatts Permutation, Variation, Kombination, Permutation mit Wiederholung oder Permutation mit Fixpunkt und der Eingabe der relevanten Werte für n (Gesamtanzahl Elemente) und k (Anzahl ausgewählter Elemente), sowie einer Bedienung der Schaltfläche Berechnen werden die Ergebnisse oben beschriebener Operationen ausgegeben.

Um Berechnungen mit Permutationen mit Wiederholung durchzuführen, müssen Eingabewerte für Elemente mit gleichen Eigenschaften (Gruppen gleicher Elemente) durch Semikola voneinander getrennt werden.
 

Allgemein

 
Durch die Bedienung der Schaltfläche Löschen können alle Eingaben und Ergebnisse gelöscht werden.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Benutzbarbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens genutzt werden.
 
Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf anschauliche Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthemengebiet.

Mittels der anschaulichen Gestaltung und leichten Bedienbarbarkeit der einzelnen Module dieser Software werden oftmals häufig gestellte Fragen mit den Anfangsworten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? zum entsprechenden Themengebiet auf verständliche Weise beantwortet und einfach erklärt sich durch dessen Benutzung vieles von alleine. Zudem liefert diese Applikation zu vielen gestellten Fragen eine verständliche Antwort, Beschreibung und Erklärung.

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Urnenmodell

Pfadregel

 

Beispiel 1 - Permutation ohne Wiederholung:

Die 8 Teilnehmer eines 100-Meter-Endlaufs kommen in einer bestimmten Reihenfolge durch das Ziel. Auf einer Anzeigetafel werden die Teilnehmer, ihrem Rangplatz entsprechend, nacheinander aufgelistet.

Wieviele mögliche Reihenfolgen gab es vor deren Ankunft im Ziel?

Anzahl Teilnehmer: n = 8

A = n! = 1*2*3*4*5*6*7*8 = 40320

Um diese Berechnung durchführen zu lassen, wählen Sie das Registerblatt Permutation-Variation-Kombination, geben die Zahl 8 in das Feld n (Gesamtanzahl Elemente) ein und bedienen die Schaltfläche Berechnen. In der Tabelle kann dieses Ergebnis unter dem Eintrag Permutation n! entnommen werden. Der eingetragene Wert im Feld k (Anzahl ausgewählter Elemente) wird ignoriert.
 

Beispiel 2 - Permutation mit Wiederholung:

Wieviele Möglichkeiten gibt es alle Buchstaben des Wortes ANAGRAMM in einer unterschiedlichen Reihenfolge anzuordnen? Verschiedene Buchstaben dieses Wortes kommen mehrfach vor.

Anzahl aller Buchstaben: n = 8

k1 = 3 (Buchstabe A)

k2 = 1 (Buchstabe G)

k3 = 1 (Buchstabe N)

k4 = 2 (Buchstabe M)

k5 = 1 (Buchstabe R)

A = 8! / (3! * 1! * 1! * 2! * 1!) = 40320 / 12 = 3360

Es besteht die Möglichkeit 3360 verschiedene Buchstabenkombinationen (Wörter) aus den Buchstaben des Wortes ANAGRAMM zu bilden.

Um diese Berechnung durchführen zu lassen, wählen Sie das Registerblatt Permutation mit Wiederholung, geben die Zahl 8 in das Feld Gesamtanzahl Elemente n ein, geben in das Feld Gruppen gleicher Elemente die Zeichenfolge 3;1;1;2;1 ein und bedienen die Schaltfläche Berechnen.
 

Beispiel 3 - Variation ohne Wiederholung:

Bei den Olympischen Spielen stehen 8 Athleten im Finale einer Sportart. Wieviele Möglichkeiten bestehen, dass diese 8 Teilnehmer die Medaillien Gold, Silber und Bronze unter sich aufteilen?

Anzahl der Teilnehmer: n = 8

Anzahl zu vergebender Medaillien: k = 3

A = n! / (n-k)! = 8! / (8 - 3)! = 336

Um diese Berechnung durchführen zu lassen, wählen Sie das Registerblatt Permutation-Variation-Kombination, geben die Zahl 8 in das Feld n (Gesamtanzahl Elemente) ein, geben im Feld k (Anzahl ausgewählter Elemente) die Zahl 3 ein und bedienen die Schaltfläche Berechnen. Aus der Tabelle kann dieses Ergebnis unter dem Eintrag Variation ohne Wiederholung entnommen werden.
 

Beispiel 4 - Variation mit Wiederholung:

Ein Zahlenschloss besteht aus 5 Vorrichtungen mit jeweils 10 Zahlen, welche jeweils eine Ziffernkombination verlangen. Bei jeder Zifferneinstellung können die Zahlen 0...9 gewählt werden.

Wieviele Möglichkeiten bestehen diesem Zahlenschloss eine Kombination zu vergeben?

Anzahl möglicher Ziffern: n = 10

Anzahl möglicher Zifferneinstellungen: k = 5

A = n^k = 10⁵ = 100000

Um diese Berechnung durchführen zu lassen, wählen Sie das Registerblatt Permutation-Variation-Kombination, geben die Zahl 10 in das Feld n (Gesamtanzahl Elemente) ein, geben im Feld k (Anzahl ausgewählter Elemente) die Zahl 5 ein und bedienen die Schaltfläche Berechnen. Aus der Tabelle kann dieses Ergebnis unter dem Eintrag Variation mit Wiederholung entnommen werden.
 

Beispiel 5 - Kombination ohne Wiederholung:

Bei der Ziehung der Lottozahlen werden von 49 nummerierten Kugeln nacheinander 6 Kugeln gezogen (ohne Zurücklegen).

Wieviele Möglichkeiten gibt es 6 Zahlen auszuwählen?

Anzahl Kugeln: n = 49

Anzahl Ziehungen: k = 6

A = n! / ( (n - k)! * k! ) = 49! / ( (49 - 6)! * 6! ) = 13983816

Um diese Berechnung durchführen zu lassen, wählen Sie das Registerblatt Permutation-Variation-Kombination, geben die Zahl 49 in das Feld n (Gesamtanzahl Elemente) ein, geben im Feld k (Anzahl ausgewählter Elemente) die Zahl 6 ein und bedienen die Schaltfläche Berechnen. Aus der Tabelle kann der errechnete Wert unter dem Eintrag Kombination mit Wiederholung entnommen werden.
 

 

Beispiel 1 - Permutation - Variation - Kombination


 Beispiel 2 - Permutation mit Wiederholung


Beispiel 3 - Permutation mit Fixpunkt
 

Beispiel 4 - Permutation - Variation - Kombination
 

Beispiel 5 - Permutation - Variation - Kombination
 

Beispiel 6 - Permutation mit Wiederholung
 

Beispiel 7 - Permutation mit Wiederholung
 

Beispiel 8 - Permutation mit Fixpunkt
 

Beispiel 9 - Permutation mit Fixpunkt

   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Kombinatorik
Wikipedia - Variation

Wikipedia - Kombination
Wikipedia - Permutation
 

Urnenmodell - Pfadregel - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Regressionsanalyse - Stichproben - Stichproben - Verteilungen - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)

 

MathProf 5.0 - Unterprogramm Pfadregel

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---