PhysProf - Pendel - Schwingung - Mathematisch - Physisch

Fachthema: Pendel - Simulation
PhysProf - Kinematik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Animation der Abläufe, welche bei der Ausführung von Fadenpendel-Schwingungen entstehen (Elongationen).
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden Sachverhalte. Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul: |
 |  |
Mathematisches Pendel (Fadenpendel) - Physisches Pendel
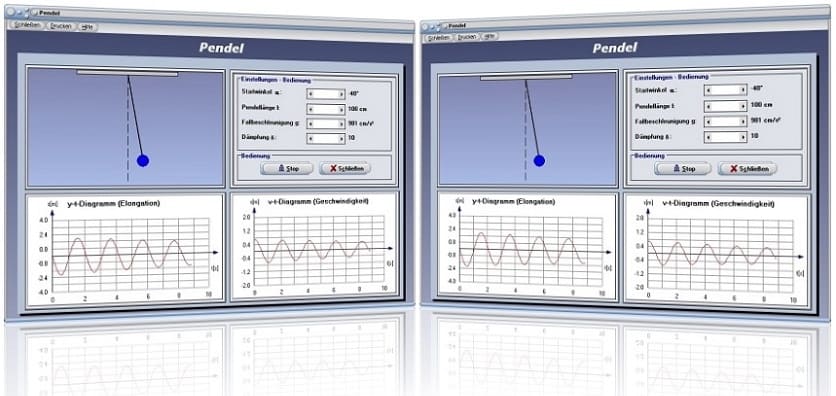
Modul Pendel
Im Unterprogramm [Mechanik I] - [Pendel] lassen sich die Abläufe einer mechanischen Schwingung beim Fadenpendel verfolgen.

Pendelbewegung - Abbildung 1

Pendelbewegung - Abbildung 2
Als Pendel wird ein Körper bezeichnet, der an einer Achse oder einem Punkt aufgehängt ist, der sich außerhalb seines Massenmittelpunkts befindet, drehbar gelagert ist und um seine Ruhelage schwingen kann.
Mechanische Schwingung: Als mechanische Schwingungen werden zeitlich periodische Änderungen einer physikalischer Größe bezeichnet. In der Mechanik werden Schwingungen als Ausführungen derartiger Bewegungen eines Körpers um seine Gleichgewichtslage beschrieben.
Schwingungen dieser Art werden hervorgerufen, wenn ein Körper aus einer Ruhelage ausgelenkt wird und eine rückwirkende Kraft zugegen ist. Eine derartige Schwingung wird als freie Schwingung bezeichnet. Seine Geschwindigkeit erreicht ein Maximum, wenn er seine Ruhelage passiert. Aufgrund der Massenträgheit verharrt der Körper nicht in dieser Position, sondern erfährt eine Elongation in die entgegengesetzte Richtung.
Mathematisches Pendel - Fadenpendel
Als mathematisches Pendel (oder Fadenpendel) wird ein Pendel bezeichnet, welches eine punktförmige Masse besitzt, die an einer masselosen Pendelstange befestigt ist. Diese Stange ist an einem Punkt aufgehängt und die daran befestigte Masse führt wechselseitige Schwingungen in der Ebene aus. Reibungseinflüsse werden hierbei vernachlässigt.
Die Schwingungsdauer eines mathematischen Pendels (welches in der Praxis nicht existiert) lässt sich ermitteln durch:

Wie hieraus zu entnehmen ist, hängt die Schwingungsdauer lediglich von der Länge l des Fadenpendels und der auftretenden Fallbeschleunigung g ab, jedoch nicht von der Masse des an das Pendel angehängten Körpers. Theoretisch lässt sich somit mit der Gleichung

und dem Zusammenhang

der Schwingungsvorgang eines Pendels dieser Art beschreiben.
Hierbei sind:
T: Schwingungsdauer [s]
ω: Schwingungsfrequenz (Pendelfrequenz) [1/s]
l: Pendellänge [m]
g: Fallbeschleunigung [m/s²]
y: Elongation [m]
ŷ: Anfangswert der Amplitudenhüllkurve [m]
Herleitung der Zusammenhänge zum mathematischen Pendel:
Bei einer linearen Federschwingung errechnet sich die Schwingungsdauer mit
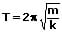
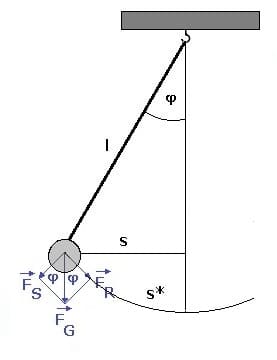
Die rücktreibende Kraft (Rückstellkraft) FR einer Pendelschwingung kann ermittelt werden, indem die Gewichtskraft FG des angehängten Körpers (Pendelkörpers) in seine Teilkräfte FS und FR zerlegt wird. Sie ist proportional zur Auslenkung des Pendels. Die Teilkraft FS bewirkt, dass der Faden gespannt bleibt, die Teilkraft FR ist die rücktreibende Kraft. Unter der Voraussetzung, dass der Auslenkungswinkel des Pendels klein ist, kann für die Länge des Kreisbogens s* näherungsweise die Strecke s angenommen werden. Bei einem kleinen Winkel gilt FR/FG = s/l, da in diesem Fall die Bogenlänge s* der Strecke s gleichgesetzt werden kann.
Hieraus folgt: FR/y = FG/l = mg/l. Somit besitzt der Term mg/l beim Fadenpendel die gleiche Bedeutung wie die Federkonstante k beim Federpendel. Resultierend aus diesen Tatsachen ergibt sich für die Schwingungsdauer des mathematischen Pendels
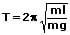
oder
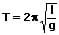
T: Schwingungsdauer [s]
m: Masse des Pendelkörpers [kg]
l: Pendellänge [m]
g: Fallbeschleunigung [m/s²]
Oben aufgeführte Herleitung gilt nur für Schwingungen mit kleinen Auslenkungswinkeln. In der Praxis wird bei einem schwingenden System Energie durch bremsende Kräfte, wie z.B. Reibung und Luftwiderstand allmählich aufgezehrt.
Eine Pendelbewegung ist die schwingende Bewegung eines Pendels.
Eine Pendelschwingung entsteht durch die Auslenkung eines Körpers, der durch die Schwerkraft in Richtung seiner Ausgangsposition beschleunigt wird und hierauf um seine Ruheposition schwingt.
Als Pendellänge l wird die gesamte Länge eines Pendels, ausgehend von dessen Aufhängungspunkt bis seinem unteren Ende bezeichnet.
Die Schwingungsfrequenz f eines Pendels gibt die Anzahl der Schwingungsvorgänge an, die dieses innerhalb des Zeitraums von 1 Sekunde ausführt. Die Zeit für die Ausführung eines Schwingungsvorgangs wird Schwingungsdauer T genannt. Es gilt: f = 1/T.
Als rücktreibende Kraft (Rückstellkraft) FR wird diejenige Kraft bezeichnet, die versucht den am Pendel angehängten Körper wieder in dessen Ausgangslage (Gleichgewichtslage) zurück zu bringen.
Als Auslenkung (Elongation) wird bei einer Schwingung die augenblickliche Distanz eines Punktes von seiner Ruhelage angegeben.
Als Abklingkonstante (Dämpfungskonstante oder Abklingkoeffizient) δ wird bei linearen Schwingungssystemen das Produkt aus ungedämpfter Eigenkreisfrequenz und Lehrscher Dämpfung bezeichnet.
Die Dämpfungskonstante beschreibt die Stärke einer Dämpfung.
Programmbedienung
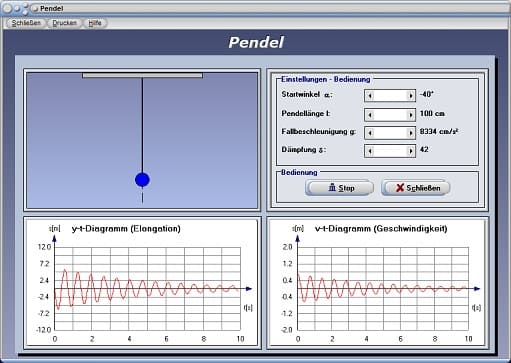
Dieses Unterprogramm simuliert den in der Praxis auftretenden Fall eines physischen Pendels und stellt in einer Grafik ein Elongations-Zeit-Diagramm und in einem anderen ein Geschwindigkeits-Zeit-Diagramm dar, wodurch das Verhalten des physikalischen Vorgangs in Abhängigkeit von den einstellbaren Größen analysiert werden kann.
Legen Sie hierfür zunächst die Werte für Startwinkel α, die Pendellänge l, die Fallbeschleunigung g, sowie die Dämpfung δ (Abklingkoeffizient) durch die Positionierung der entsprechenden Rollbalken fest und bedienen Sie hierauf die Schaltfläche Start. Durch die Ausführung eines erneuten Klicks auf diese Schaltfläche, welche hierauf die Bezeichnung Stop besitzt, beenden Sie die ablaufende Simulation wieder.
Hinweis: Besäße die Dämpfungskonstante den Wert 0, so würde das System keine Dämpfung erfahren und somit ein perpetuum mobile darstellen.
Physisches Pendel
Als physisches Pendel (unkorrekte Bezeichung: physikalisches Pendel) wird ein Pendel benannt, bei welchem die Voraussetzungen des mathematischen Pendels nicht erfüllt sind.
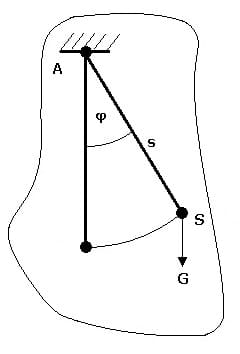
Bei diesem gilt.
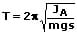
T: Schwingungsdauer [s]
m: Masse des Pendelkörpers [kg]
JA: Massenträgheitsmoment des Pendelkörpers [kg·m²]
s: Abstand des Drehpunkts vom Massenschwerpunkt des Pendelkörpers [m]
Die obige Formel hat nur Gültigkeit für Amplituden, die kleiner als ca. 8° sind. Mit dem Begriff reduzierte Pendellänge (eines physischen Pendels) wird die Länge eines mathematischen Pendels bezeichnet, welches dieselbe Schwingungsdauer besitzt. Sie entspricht der Länge l in der Schwingungsgleichung des mathematischen Pendels.
Doppelpendel - Gekoppelte Schwingungen
Werden zwei oder mehrere Pendel durch eine Feder miteinander verbunden, so wird diese Anordnung als gekoppeltes Pendel bezeichnet. Eine derartige Anordnung zweier Pendel wird Doppelpendel genannt. Schwinger dieser Art sind nicht mehr voneinander unabhängig, da sie durch ihre Kopplung gegenseitig Energie austauschen. Dieser Austausch kann über Reibung, Elastizität oder Trägheit erfolgen. Die von einem Doppelpendel ausgeführten Schwingungen werden als gekoppelte Schwingungen bezeichnet.
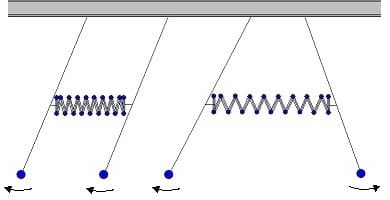
Wird eines dieser Pendel durch Auslenkung zum Schwingen gebracht, so erfolgt die Übertragung seiner Energie allmählich an das zweite Pendel. Dies erfolgt so lange, bis sich das erste Pendel in Ruhelage befindet (im Nulldurchgang oder Umkehrpunkt) und die gesamte (im System noch vorhandene) Energie an das zweite Pendel übertagen wurde.
Hierauf erfolgt die gegenseitige Vertauschung der Aufgaben, wobei das nun ruhende Pendel durch das noch schwingende Pendel angeregt wird und dessen Schwingungsenergie diesem übertagen wird. Durch die im System vorhandene Schwingungsenergie werden somit wechselnde Zustände der Ruhelage und der Maximalauslenkung der einzelnen Pendel zustande kommen, bis die im System vorhandene mechanische Energie u.a. durch Reibungsverluste aufgezehrt wurde.
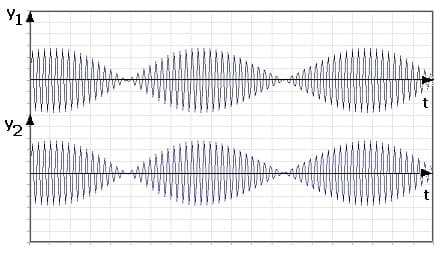
Es existieren zwei Fälle dieses Systems, bei denen es zu keinem Energieaustausch zwischen den beiden Pendeln kommt. Dies sind:
- Gleichsinnige Schwingung: Beide Pendel schwingen mit gleicher Amplitude und gleicher Phase mit ihrer normalen Eigenfrequenz.
- Gegensinnige Schwingung: Beide Pendel schwingen mit gleicher Amplitude, jedoch gegenphasig und mit höherer Frequenz.
Voraussetzung dafür, dass dieses gekoppelte System wie oben beschrieben ausgeführt wird, ist dass die beiden Pendel exakt aufeinander abgestimmt sind, denn ansonsten führt es unter Umständen chaotische Bewegungen aus.
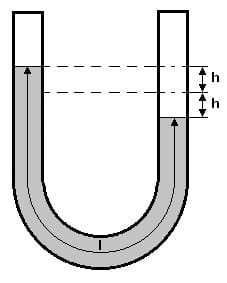
Schwingung im U Rohr - Wasserpendel
Ein Wasserpendel, welches als U-Rohr geformt ist und in dem eine zuvor ausgelenkte Wassersäule schwingt, führt solange eine harmonische Schwingung aus bis diese sich im wieder Gleichgewichtszustand befindet. Dieses Pendel wird auch als schwingende Flüssigkeitssäule bezeichnet
Für die Schwingungsdauer eines derartigen Systems gilt:
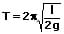
T: Schwingungsdauer [s]
l: Länge der Flüssigkeitssäule [m]
g: Fallbeschleunigung [m/s²]
Die Schwingungsdauer eines Wasserpendels ist unabhängig von der Fläche, der Dichte der Flüssigkeit und der Höhe der Flüssigkeitssäule. Sie hängt lediglich von der Länge dieser ab. Sie ist identisch mit der eines mathematischen Pendels, welches die Länge eines Säulenschenkels besitzt.
Pendelbewegung - Abbildung 3
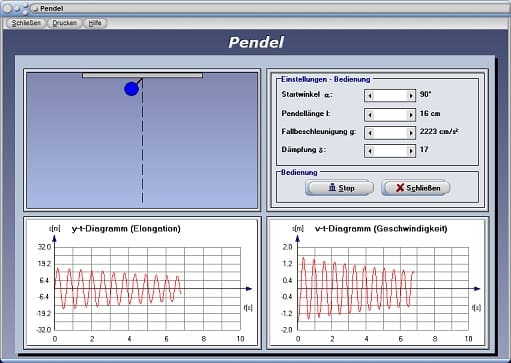
Pendelbewegung - Abbildung 4
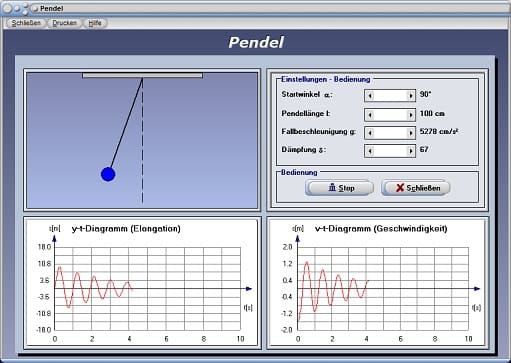
Pendelbewegung - Abbildung 5
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung oder einem Beweis zu folgen.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Pendel sowie Wikipedia - Mathematisches Pendel unter zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
Unterprogramm Pendel

PhysProf 1.1 - Unterprogramm RLC-Kreis

MathProf 5.0 - Unterprogramm Kurven in Parameterform

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















