MathProf - Kurvendiskussion - Differentialrechnung - Extremstellen

Fachthemen: Kurvendiskussion - Differentialrechnung - Ableitung
MathProf - Analysis - Software für höhere Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung von Kurvendiskussionen.
Dieses Teilprogramm ermöglicht die Anwendung der Funktionsuntersuchung (Funktionsanalyse) expliziter Funktionen hinsichtlich vieler hierfür relevanter Eigenschaften sowie das Zeichnen derer Graphen und Ableitungsfunktionen.
Hierbei erfolgt neben der Ausführung der numerischen Differentiation und der grafischen Ausgabe derer Resultate die Darstellung der zugehörigen Steigungsfunktion sowie höherer Ableitungen.
Der implementierte Nullstellenrechner erlaubt das Ermitteln der Nullstellen einer definierten Funktion. Auch vollzieht dieses Programmmodul das Berechnen der Extrema, der Wendepunkte und der Polstellen dieser. Es erlaubt es zudem, Funktionen auf deren wesentliche Eigenschaften hin zu untersuchen.
Darüber hinaus erfolgt die Bestimmung der vorliegenden Art der Krümmung in relevanten Kurvenpunkten und die Ausgabe des Krümmungsmittelpunkts und des Krümmungsradius des Krümmungskreises an diesen Stellen.
Auch wird vom Rechner die Untersuchung durchgeführt, ob es sich bei der ausgegebenen Kurve um eine konkave Funktion, oder eine konvexe Funktion handelt und es kann das Steigungsverhalten sowie das Krümmungsverhalten (Linkskrümmung oder Rechtskrümmung) dieser analysiert werden.
Des Weiteren werden wesentliche Eigenschaften einer definierten Funktion ausgegeben, welche diese bei den ermittelten charakteristischen Kurvenpunkten besitzt. Die vom Programm berechneten Lösungen werden in einer Tabelle ausgegeben.
Dieses Unterprogramm eignet sich zum Lösen vieler Aufgaben aus dem Bereich der Kurvenuntersuchung und es sind Beispiele hierzu eingebunden.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte I zu diesem Modul:Kurvendiskussion - Funktionsuntersuchung - Kurvenuntersuchung - Differenzieren - Extrempunkte - Komplette Kurvendiskussion - Ableitung - Ableitungen - Extremalprobleme - Extremalprobleme - Extremwertproblem - Extremwertprobleme - Ableitungsgraph - Krümmungskreis - Funktion - Funktionen - Lokale Extrema - Lokale Extremstellen - Funktionsanalyse - Bestimmen - Randextrema - Funktionen ableiten - Ableitung berechnen - Ableitung bestimmen - Ableitung einer Funktion - Beispielaufgabe - Funktion ableiten - Polstellen - e-Funktionen - ln-Funktionen - Erste Ableitung - Zweite Ableitung - Dritte Ableitung - Vollständige Kurvendiskussion - Komplett - e-Funktion - ln-Funktion - Zusammenhang - Ableitungsregeln - Extremwertaufgaben - Maxima - Minima - Analysis - Formeln - Steigung - Wertebereich - Formelsammlung - Zeichnen - Erklärung - Einfach erklärt - Bedeutung - Was bedeutet - Was - Wie - Weshalb - Warum - Welche - Welcher - Welches - Wodurch - Beschreibung - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Begriff - Begriffe - Mathe - Mathematik - Schreibweise - Anwendungsaufgaben - Definition - Hinreichende Bedingung - Notwendige Bedingung - Funktion untersuchen - Lokale Minima - Lokale Maxima - Lokale und globale Extrema - Wurzel - Logarithmus - Potenzfunktion - Sinusfunktion - Winkelfunktionen - Graphische Ableitung - Graphisches Ableiten - Ableitungen bilden - Numerisch ableiten - Numerisch differenzieren - Numerische Differentiation - Rechnerisch bestimmen - Grafisch - Vollständige Funktionsuntersuchung - Infinitesimalrechnung - Übersicht |
Themen und Stichworte II zu diesem Modul:1. Ableitung - 2. Ableitung - 3. Ableitung - Ableitungsfunktionen - Ableitungsfunktion - dy/dx - Differential - Extremwertberechnung - Krümmungsverhalten - Verlauf - Untersuchen - Untersuchung - Bild - Grafik - Extrema - Extremwerte - Extremstellen - Lokales Extremum - Wendetangente - Wendenormale - Wendepunkt - Wendestelle - Hochpunkt - Tiefpunkt - Punkte - Finden - Merkmale - Anwendung - Steigungsverhalten - Konvexe Funktion - Konkave Funktion - Krümmung - Linkskrümmung - Rechtskrümmung - Allgemein - Relative Extremwerte - Relativer Hochpunkt - Relativer Tiefpunkt - Relatives Maximum - Relatives Minimum - Hochpunkte - Tiefpunkte - Extrema - Extremstellen - Wendepunkte - Charakteristische Punkte - Tabelle - Berechnen - Bestimmen - Bestimmung - Rechner - Funktionsrechner - Rechnerisch - Plotter - Graph - Funktion - Minimalstelle - Maximalstelle - Ableiten - Analyse - Gesetze - Regel - Ableitungen - Höhere Ableitungen - Ableitungstabelle - Erstellen - Ermittlung - Herleitung - Werte - Zeichnerisch - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Einführung - Lernen - Erlernen - Übungsaufgaben - Anwendungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Rechnerische Bestimmung - Differenzierbarkeit - Grafisches Differenzieren - Analysieren - Differenzierbare Funktion - Grafisches Ableiten - Graphisches Ableiten - Plotten - Regeln - Pole - Normale - Tangente - Zeichnerisch ableiten - Zeichnerisch differenzieren - Zeichnerisches Ableiten - Zeichnerisches Differenzieren - Ableitungsregel - Potenzregel - Summenregel - Differenzregel - Produktregel - Quotientenregel - Anwenden - Anwendung - Herleitung - Beweis - Brüche ableiten - Bruch ableiten - Übersicht - Spezielle Ableitungen - Partiell - Partielle Ableitung - Partielle Ableitung 1. Ordnung - Partielle Ableitung 2. Ordnung - Partielle Differentiation - Partielles Ableiten - Bilder - Beispiel - Aufgabe - Abituraufgaben - Beispielaufgaben - Grundlagen - Grundlegendes - Darstellung - Extremum - Sattelpunkt - Terrassenpunkt - Bedingungen - Extremwertbestimmung - Berechnung - Darstellen - Krümmungswechsel - Positive Krümmung - Negative Krümmung - Intervalle - Vorzeichenwechsel - Vorzeichenwechselkriterium - VZW - Flachpunkt - Flachpunkte - Kriterien - Kriterium - Spezielle Ableitungen - Vertauschen - Variablen - Umkehrfunktion - Monotonie - Monotoniekriterium - Monotonieverhalten - Monotonie bestimmen - Streng monoton steigend - Streng monoton fallend - Monoton steigend - Monoton fallend - Satz von Rolle - Mittelwertsatz - Verallgemeinerter Mittelwertsatz - Differentialgeometrie - Anwendungsbeispiele - Merksatz - Merksätze - Steigend - Fallend - Hoch- und Tiefpunkte berechnen - Ableitung bilden - Erste Ableitung bilden - Zweite Ableitung bilden |
Themen und Stichworte III zu diesem Modul:Substitution - Substituieren - Substitutionsverfahren - Substitutionsmethode - Abgeleitet - Logarithmische Differentiation - Logarithmische Ableitung - Logarithmisches Differenzieren - Wurzeln - Wurzel ableiten - Defintionsbereich - Lösung - Verhalten - Kettenregel - Klammer - Klammern - Innere Ableitung - Äußere Ableitung - Konstantenregel - Faktorregel - Äußere Funktion - Innere Funktion - Verkettete Funktionen - Kurvenschar - Kurvenscharen - Reziprokenregel - Kehrwertregel - arctan - arcsin - arccos - arcsinh - Grundregeln - Hoch x - Hoch 1/2 - Ableiten nach x - sin - cos - x Quadrat - a^x - a hoch x - Dritte Wurzel - e hoch x -ln e - ln Funktion - Logarithmus - Sinus - Tan - Trigonometrische Funktionen - tan(x) - Zahl - Abgeleitet - f(x) - lg - sin(x) - tan - Tangens - Wurzel x - a^x - Betrag - f Strich - f zwei Strich - Arccot - Ln - Log - Sinh - Cosh - Tanh - Coth - Arsinh - Arcosh - Artanh - Arcoth - Cot - Tan - 1/ln(x) - 1/log(x) - 1/cos(x) - 1/e - 1/e^2 - 1/e^x - 1/x - e Funktion - Arcussinus - Arcuscosinus - Arcustangens - x^n - cos(x) - sin(x) - tan(x) - cot(x) - arcsin(x) - arccos(x) - arctan(x) - arccot(x) - e^x - a^x - ln(x) - log(x) - sinh(x) - cosh(x) - arsinh(x) - arcosh(x) - artanh(x) - arcoth(x) - Exp - Exp(x) - Exp(1/x) - Exp(x^2) - Quadratische Funktion - Log ableiten - 2te Ableitung - 3te Ableitung - Schreibweise - Anwendung - Anwenden - Potenzfunktion - Logarithmusfunktion - Wurzelfunktion - Potenzfunktionen - Logarithmusfunktionen - Potenzfunktionen - Wurzelfunktionen |
Kurvendiskussion - Differentialrechnung - Ableiten
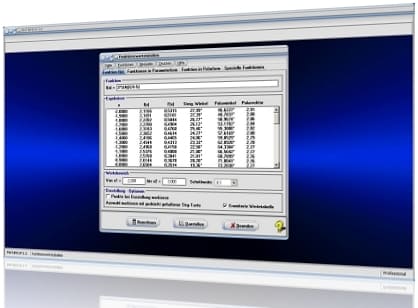
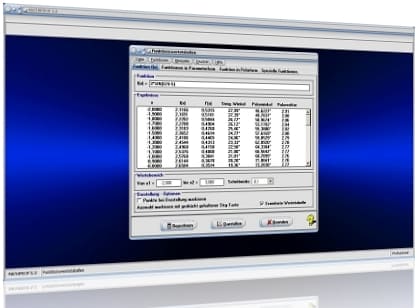
Modul Kurvendiskussion
Im Programmteil [Analysis] - [Kurvendiskussion] - Kurvendiskussion (Funktionsuntersuchung und Differentialrechnung) wird die Durchführung von Analysen zum Berechnen von Nullstellen, Extrempunkten, Wendepunkten (Wendestellen) und weiterer Eigenschaften mathematischer Funktionen in expliziter Form ermöglicht. Zudem wird das Ableiten (Differenzieren) definierter Funktionen ermöglicht.

Die Differentialrechnung (Differenzialrechnung) ist ein wesentlicher Bestandteil der Analysis und setzt sich mit der Berechnung lokaler Veränderungen von Funktionen auseinander. Den Grundbaustein der Differenzialrechnung stellt die Ableitung einer Funktion dar. Gemeinsam mit der Integralrechnung bildet sie den Berech der Infinitesimalrechnung.
Unter dem Begriff Kurvendiskussion wird die Durchführung von Untersuchungen des Graphen einer mathematischen Funktion verstanden. Anwendung findet die Kurvendiskussion bei der Durchführung von Analysen zur Ermittlung wesentlicher Eigenschaften derer. Hierzu zählen unter anderem die Ermittlung der Nullstellen, Extrempunkte (Minima und Maxima), Wendepunkte und Polstellen der entsprechenden Funktion. Des Weiteren werden deren Symmetrieeigenschaften sowie ihr Verhalten analysiert.
Das Programm führt in diesem Modul eine numersiche Differentiation (Differentialrechnung) durch und untersucht hierbei Funktionen der Form y = f(x) auf folgende Punkte und mathematische Eigenschaften:
- Nullstellen
- Pole (Polstellen)
- Lokale Extrema / Lokale Extrempunkte (Hochpunkte und Tiefpunkte, Maxima und Minima)
- Wendepunkte (Wendestellen)
Zudem werden ausgegeben:
- Eigenschaften der mathematischen Funktion
- Koordinaten des Schnittpunkts der Kurve mit der Y-Achse
- Steigung der Tangenten in ermittelten Kurvenpunkten
- Gleichungen der Tangenten und Normalen in ermittelten Kurvenpunkten
- Art der Krümmung an ermittelten Kurvenpunkten
- Eigenschaften der durch Extremstellen (Extrempunkte) und Nullstellen verlaufenden Krümmungkreise
Grafisch darstellen lassen sich:
- Die zu untersuchende Funktion f(x,p)
- 1. Ableitung (erste Ableitung) f'(x,p) (Ableitungsfunktion, Steigungsfunktion) der zu untersuchenden Funktion f(x,p)
- 2. Ableitung (zweite Ableitung) f''(x,p) (Ableitungsfunktion) der zu untersuchenden Funktion f(x,p)
- 3. Ableitung (dritte Ableitung) f'''(x,p) (Ableitungsfunktion) der zu untersuchenden Funktion f(x,p)
- Polstellen (Pole) der zu untersuchenden Funktion f(x,p)
- Tangenten in Nullstellen, Extremstellen (Extremwerte, Extrempunkte) und Wendepunkten (Wendestellen) der zu untersuchenden Funktion f(x,p)
- Normalen in Nullstellen, Extremstellen (Extremwerte, Extrempunkte) und Wendepunkten (Wendestellen) der zu untersuchenden Funktion f(x,p)
- Krümmungskreise durch Nullstellen und Extremstellen (Extremwerte, Extrempunkte) der zu untersuchenden Funktion f(x,p)
Nachfolgend wird auf einige grundlegende Zusammenhänge und Sachverhalte zu diesem Fachthema eingegangen.
Nullstellen - Hochpunkte - Tiefpunkte - Wendepunkte - Pole - Krümmung
Erklärung themenrelevanter Fachbegriffe:
Nullstellen sind Punkte, in welchen eine Funktion f(x) die x-Achse schneidet bzw. berührt und der Funktionswert gleich 0 ist.
Extrema (Hochpunkte und Tiefpunkte) sind Punkte einer Kurve, bei denen eine Funktion lokale Maxima bzw. Minima besitzt. Punkte dieser Art werden auch als lokale Extrema, relative Extremwerte oder lokale Minima bzw. lokale Maxima bezeichnet. Stellen an denen derartige Punkte vorhanden sind, tragen auch die Bezeichnungen lokale Extremstellen, Minimalstelle oder Maximalstelle.
Ein Punkt welcher der höchste seiner Art in dessen Umgebung (in einem definierten Bereich) ist, wird als absoluter Hochpunkt bezeichnet. Für andere Hochpunkte in diesem Bereich werden die Bezeichnungen relativer Hochpunkt (relatives Maximum oder lokales Maximum) verwendet, da sie nur das Maximum innerhalb eines bestimmten Bereichs darstellen.
Der allertiefste Punkt (Minimum) ist der absolute Tiefpunkt und andere Punkte dieser Art in dieser Umgebung werden mit der Bezeichnung relatives Minimum oder lokales Minimum bezeichnet. Andere Punkte dieser Art tragen die Bezeichnung relative Tiefpunkte.
Die Ermittlung von Extremwerten wird als Extremwertberechnung oder Extremwertbestimmung bezeichnet.
Bei einem Wendepunkt handelt es sich um einen Punkt einer Funktion, in dem sich das Krümmungsverhalten des Graphen der Funktion ändert. In Wendepunkten liegt eine Änderung der Art der Kurvenkrümmung vor, d.h. eine Kurve geht von einer Links- in eine Rechtskurve, oder umgekehrt, über. In diesen Punkten ändert sich der Drehsinn der Kurventangente.
Wendepunkte, die eine horizontal verlaufende Tangente besitzen werden als Sattelpunkte bezeichnet. Die durch einen Wendepunkt verlaufende Tangente heißt Wendetangente. Als Wendenormale wird die Normale bezeichnet, die durch einen Wendepunkt verläuft.
Pol: Pole sind Definitionslücken besonderer Art. Nähert man sich einer Stelle dieser Art, so strebt der Funktionswert an dieser Stelle gegen plus unendlich oder gegen minus unendlich.
Differenzieren: Unter dem Begriff Differenzieren wird das Ableiten einer Funktion verstanden. Dies bedeutet ihre Ableitung zu bestimmen bzw. deren Steigung an einer bestimmten Stelle zu ermitteln. Es wird unterschieden zwischen dem numerischen Differenzieren und dem grafischen Differenzieren.
Numerische Differentiation (numerisch differenzieren): Als numerische Differentiation wird die näherungsweise Berechnung der Ableitung einer Funktion aus gegebenen Funktionswerten mittels eines Differenzenquotienten bezeichnet. Für die Anwendung dieser Methode werden auch die Begriffe numerisch differenzieren oder numerisch ableiten verwendet. Das Berechnen der Ableitung f' wird als Differentiation bezeichnet.
Ableitungsgraph: Unter dem Begriff Ableitungsgraphen wird die grafische Darstellung der ersten und / oder zweiten Ableitung einer Funktion verstanden.
Funktionsanalyse: Der Sinn der Durchführung einer Funktionsanalyse ist es, die wesentlichsten Eigenschaften einer Funktion zu ermitteln. Für diesen Vorgang wird auch der Begriff vollständige Funktionsuntersuchung verwendet.
Randextrema: Besitzt eine Funktion ihren höchsten oder ihren niedrigsten Wert am Randbereich einer durchgeführten Untersuchung, so wird von einem Randextremum gesprochen.
Ableitungsfunktionen: Die 1. Ableitung einer Funktion f'(x) wird auch als Ableitungsfunktion bezeichnet.
Differential: Ein Differential (Differenzial) bezeichnet den linearen Anteil des Zuwachses einer Variablen oder einer mathematischen Funktion.
Konvexe Funktion: Eine reellwertige Funktion heißt konvex (nach oben oder unten gewölbt), wenn ihr Graph unterhalb jeder Verbindungsstrecke zweier seiner Punkte liegt. Dies ist identisch dazu, dass es sich bei der Menge der Punkte oberhalb des Graphen um eine konvexe Menge handelt.
Konkave Funktion: Eine reellwertige Funktion heißt konkav (gewölbt), wenn ihr Graph oberhalb jeder Verbindungsstrecke zweier seiner Punkte liegt. Dies ist identisch dazu, dass es sich bei der Menge der Punkte unterhalb des Graphen um eine konvexe Menge handelt.
Wendestellen: Als Wendestelle wird der Abszissenwert eines Wendepunkts bezeichnet. Wendestelle und Wendewert bilden gemeinsam einen Wendepunkt
Charakteristische Punkte: Als charakteristische Punkte einer Funktion werden deren Hoch- und Tiefpunkte sowie deren Wendepunkte bezeichnet.
Flachpunkte: Ein Flachpunkt ist ein Punkt bei dem gilt: f''(x) = 0. Es handelt sich um eine Stelle bei der die zweite Ableitung der Funktion den Wert 0 besitzt. Die Steigung der Kurve ändert sich in einem derartigen Punkt nicht.
Graphisches Ableiten: Mit dem Begriff grafisches Ableiten (grafisches Differenzieren) wird die Methode bezeichnet, mit der aus dem gegebenen Graphen einer Funktion der Graph der ersten Ableitung dieser hergeleitet wird, ohne die Gleichung der Ausgangsfunktion oder der Ableitungsfunktion zu kennen oder zu nutzen. Hierbei werden Aussagen über den Verlauf einer Funktion gemacht, die aus dem Verlauf ihrer 1. und 2. Ableitung gefolgert werden können. Dieses Vorgehen wird auch als zeichnerisch Differenzieren, zeichnerisches Differenzieren oder zeichnerisches Ableiten bezeichnet.
Basis für diese Vorgehensweise ist die Tatsache, dass die Ableitungsfunktion f‘(x) einer Funktion f(x) an jeder Stelle deren Tangentensteigung beschreibt. Durch entsprechende Eigenschaften der Funktion f(x) können hierdurch konkrete Aussagen hinsichtlich des Graphen von f‘(x) gemacht werden. Anhand dieser Informationen über den Verlauf des Graphen der Ableitungsfunktion kann dieser hierauf grob skizziert werden.
Funktionsuntersuchung (Kurvenuntersuchung) Funktionsanalyse: Der Sinn der Durchführung einer Funktionsanalyse ist es, die wesentlichsten Eigenschaften einer Funktion zu ermitteln. Hierzu wird eine komplette Kurvendiskussion (vollständige Kurvendiskussion) durchgeführt. Diese umfasst die nachfolgend aufgeführten wesentlichen Aufgaben:
- Bestimmung der 1. Ableitung f'(x)
- Bestimmung der 2. Ableitung f''(x)
- Untersuchung auf einfache Symmetrieeigenschaften
- Bestimmung der Nullstellen der Funktion f(x) sowie des Schnittpunkts derer mit der y-Achse
- Analyse des globalen Verhaltens der Funktion f(x) für |x|→∞
- Ermittlung der Extrempunkte der Funktion f(x)
- Ermittlung der Wendepunkte der Funktion f(x)
- Darstellung (Schaubild) der Funktion f(x) sowie derer 1. und 2. Ableitung
Differenzial - Differenzierbarkeit - Linksseitige Ableitung - Rechtsseitige Ableitung - Differenzialoperator - Schreibweise
Eine Funktion f ist in x0 differenzierbar, wenn sie in der Umgebung von x0 definiert ist und der Grenzwert
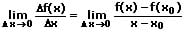
existiert. Jede an der Stelle x0 differenzierbare Funktion ist dort auch stetig (hinreichende, nicht notwendige Bedingung). Dies gilt nicht umgekehrt. Die Differenzierbarkeit einer Funktion an der Stelle x0 bedeutet, dass die Kurve dieser Funktion an dieser Stelle über eine eindeutig bestimmbare Tangente mit endlicher Steigung verfügt.
Linksseitige Ableitung:
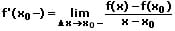
Rechtsseitige Ableitung:
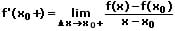
Sind an der Stelle x0 die links- und rechtsseitige Ableitung verschieden, so ist die Funktion an der Stelle x0 nicht differenzierbar.
Eine Funktion f ist im Intervall I = (a,b) differenzierbar, wenn sie an jeder Stelle innerhalb I differenzierbar ist.
Eine Funktion f ist auf dem Intervall I = [a,b] differenzierbar, wenn sie an jeder Stelle innerhalb I und auch in a und b einseitig differenzierbar ist.
Die erste Ableitung (1. Ableitung) von f in (a,b) ist die Funktion f' die alle geordneten Paare (x,f(x)), x ∈ (a,b) enthält. Ist f' stetig, nennt man f stetig differenzierbar auf (a,b).
Ist f für alle x ∈ d(f) differenzierbar, so gilt: x → f'(x)
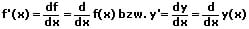
Erste Ableitung von f (gelesen 'df nach dx')
d/dx heißt der Differenzialoperator, der die erste Ableitung erzeugt.
Das Differenzial dy einer differenzierbaren Funktion f ist die Änderung der Tangentenkoordinate, der Zuwachs auf der Tangente:
dy = f'(x) dx
Es beschreibt den Anstieg des Ordinatenwerts an der Stelle x auf der Tangente der Kurve, wenn sich der Abszissenwert um dx verändert. dy heißt das Differenzial der Funktion y = f(x) das zum Inkrement Δx = dx gehört.
Ableitungen - Ableitungstabelle - Übersicht - Grundlagen - Spezielle Ableitungen - Formelsammlung - Formeln - Ableiten - Differenzieren - Ableitung bilden - Abgeleitet - Übersicht
In der nachfolgend aufgeführten Tabelle finden Sie eine Übersicht der ersten Ableitungen elementarer Funktionen (Gesetze und Regeln algebraisch), welche bei der Durchführung der symbolischen Differentiation Anwendung finden:
Elementare Funktionen und deren erste Ableitungen (elementare Ableitungen):
| Funktion f(x) | Ableitung f'(x) |
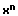 | 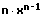 |
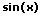 | 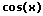 |
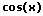 | 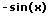 |
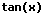 | 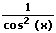 |
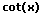 | 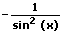 |
 | 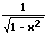 |
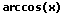 | 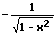 |
 | 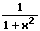 |
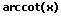 | 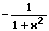 |
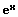 | 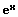 |
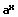 | 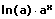 |
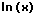 | 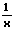 |
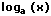 | 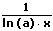 |
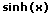 | 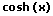 |
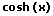 | 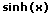 |
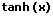 | 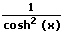 |
 | 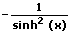 |
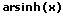 | 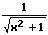 |
 | 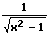 |
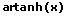 | 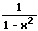 |
 | 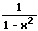 |
Ableiten - Ableitungsregeln - Differentiationsregeln - Regeln - Potenzregel - Faktorregel - Summenregel - Differenzregel - Produktregel - Konstantenregel - Quotientenregel - Kettenregel - Bruch ableiten - Innere Ableitung - Äußere Ableitung - Konstantenregel - Faktorregel
Funktionen ableiten: Im Weiteren erfolgt die Ausgabe der Ableitungsregeln, welche bei der Durchführung der symbolischen Differentiation gelten. Unter deren Anwendung erfolgt das Bilden (Bestimmen) der Ableitung einer Funktion.
1. Die Ableitung einer Konstante:
Die Ableitung einer konstanten Funktion ist Null.
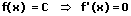
Beispiele:
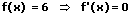
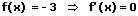
2. Die Ableitung von x:
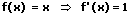
Beispiele:
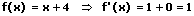
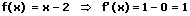
3. Die Potenzregel:
Die Potenzregel besagt, dass die Ableitungsfunktion einer Funktion f(x) = xn durch f′(x) = n⋅xn−1 gegeben ist. Dabei ist n ≠ 0 eine ganzzahlige natürliche Konstante.
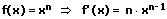
Beispiele:
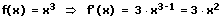
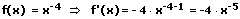
4. Die Faktorregel:
Die Faktorregel besagt: Der konstante Faktor a bleibt bei der Differentiation unberücksichtigt.

Beispiele:
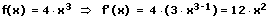
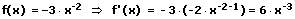
5. Die Summenregel:
Die Summenregel besagt: Die Ableitung einer Summe endlich vieler Funktionen ist gleich der Summe der Ableitungen der Summanden.
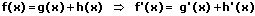
Beispiele:
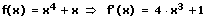
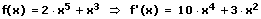
6. Die Differenzregel:
Die Differenzregel besagt: Die Ableitung einer Differenz endlich vieler Funktionen ist gleich der Differenz der Ableitungen der Minuenden.

Beispiele:
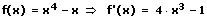
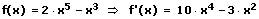
7. Die Produktregel:
Die Produktregel lautet: Das Produkt zweier Funktionen wird abgeleitet, indem das Produkt aus der Ableitung der ersten Funktion mit der zweiten Funktion zum Produkt der ersten Funktion mit der Ableitung der zweiten Funktion addiert wird.
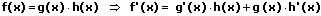
Beispiel:
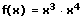
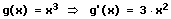
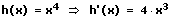
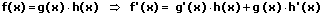
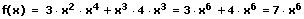
8. Die Quotientenregel (Brüche ableiten - Bruch ableiten):
Die Quotientenregel besagt, dass vom Produkt aus der Ableitung des Zählers f'(x) mit der Nennerfunktion g(x) das Produkt aus der Zählerfunktion multipliziert mit der abgeleiteten Nennerfunktion zu bilden ist und diese Differenz durch das Quadrat der Nennerfunktion zu dividieren ist.
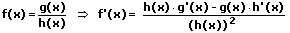
Beispiel:
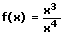
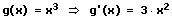
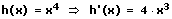
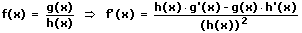
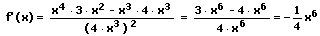
9. Die Kettenregel:
Die Kettenregel findet Anwendung, wenn zwei Funktionen v(x) und u(x) miteinander verkettet sind. Dies ist der Fall, wenn sich eine Funktion f(x) aus einer äußeren Funktion v(x) sowie einer inneren Funktion u(x) zusammensetzt. Sie besagt, dass die Ableitung einer verketteten Funktion gleich dem Produkt der Ableitungen von äußerer und innerer Funktion an der jeweiligen Stelle ist.
f(x) = v(u(x))
f'(x) = v'(u(x))·u(x)
Beispiel:
Es gilt, die erste Ableitung der nachfolgend gezeigten Wurzelfunktion zu bilden:
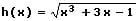
Diese Funktion besteht aus den zwei verknüpften Funktionen g(x) und f(x):
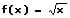
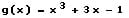
Hierbei ist f(x) die äußere Funktion und g(x) die innere Funktion. Zur Bildung der ersten Ableitung h'(x) sind die beiden Funktionen f(x) sowie g(x) zunächst separat abzuleiten. Es folgt:
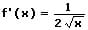
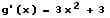
Die Ableitung h'(x) wird gebildet, indem g(x) sowie f(x) in das obige Ergebnis eingebunden wird und dieses mit g(x) multipliziert wird. Somit lautet die 1. Ableitung des oben gezeigten Terms wie folgt:
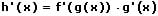
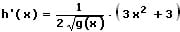
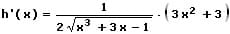
10. Die Konstantenregel:
Die Konstantenregel findet Anwendung, wenn sich vor der abzuleitenden Funktion f(x) ein konstanter Faktor c befindet. Sie besagt, dass ein konstanter Faktor beim Differenzieren unberücksichtigt bleibt.
g(x) = c·f(x)
g'(x) = c·f'(x)
Beispiel:
f(x) = 3x4
f'(x) = 3·(x4)' = 3·4·x3 = 12·x3
11. Die Reziprokenregel - Kehrwertregel:
Die Kehrwertregel (Reziprokenregel) ist eine Variante der Quotientenregel und definiert, wie der Kehrwert einer Funktion der Form 1/f(x) abgeleitet wird. Sie besagt, dass der negative Quotient aus einer abgeleiteten Funktion f'(x) mit dem Quadrat der Funktion f2(x) zu bilden ist. Sie lautet:
(1/f(x))' = -f'(x)/f²(x)
Befindet sich im Zähler nicht die Zahl 1, sondern eine Konstante c so gilt:
(c/f(x))' = -c·f'(x)/f²(x)
Beispiel:
f(x) = 1/(x² + 1)
Zähler: 1
Nenner: x2 + 1
Erste Ableitung des Nenners: f'(x) = 2x
Quadrat der Funktion f(x): f²(x) = (x² + 1)² = x4 + 2x2 + 1
Hieraus folgt für die Kehrwertfunktion der oben gezeigten Funktion f(x) = 1/(x² + 1):
(1/f(x))' = 2x/(x4 + 2x2 + 1)
Ableitung einer Wurzelfunktion
Nachfolgend wird auf das prinzipielle Vorgehen zur Bildung der ersten Ableitung einer Wurzelfunktion eingegangen.
Eine Wurzel kann wie folgt in Form eines Exponenten ausgedrückt werden:
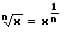
Es gilt:
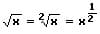
Aus diesem Grund lässt sich eine Wurzel mit Hilfe der Potenzregel ableiten:
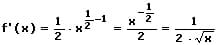
Um eine Wurzel, welche mehr als ein Argument besitzt, abzuleiten, wird die Kettenregel benötigt. Hierbei ist die äußere Funktion die Wurzel und die innere Funktion der Term, welcher sich unter der Wurzel befindet. Zwei verkettete Funktionen f(x) und g(x) werden gemäß der folgenden Vorschrift abgeleitet:
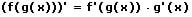
Beispiel:
Gegeben sei die folgende Funktion h(x):
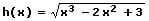
Diese wird gemäß der Kettenregel abgeleitet. Hierzu werden zunächst die äußere Funktion f(x) sowie die innere Funktion g(x) bestimmt und hierauf abgeleitet.
Äußere Funktion f(x):
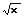
Ableitung der äußeren Funktion f(x) - Äußere Ableitung:
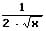
Innere Funktion g(x):
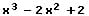
Ableitung der inneren Funktion g(x) - Innere Ableitung:
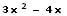
Durch Anwendung dieser Rechenvorschrift resultiert hieraus für die 1. Ableitung der oben gezeigten Wurzelfunktion h(x):
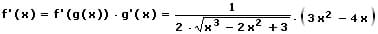
Ableitung einer Umkehrfunktion
Ermittlung der 1. Ableitung einer Umkehrfunktion:
Ist y = f(x) eine umkehrbare Funktion und x = g(y) die nach der Variable x aufgelöste Form von y = f(x), so besteht zwischen den Ableitungen f'(x) und g'(y) folgende Beziehung:
f'(x)·g'(y) = 1
bzw.
g'(y) = 1/f'(x)
Hieraus lässt sich nach folgendem Schema die Ableitung g'(x) der Umkehrfunktion y = g(x) bestimmen.
1. Ableiten der Funktion f(x)
2. Umstellen der Funktion f(x) nach x
3. Einsetzen von f'(x) in g'(y)
4. Ausdruck von f'(x) durch y ersetzen
5. Beidseitiges Vertauschen der Variablen x und y
Beispiel:
Gegeben sei die Funktion y = f(x) = tan(x). Es gilt die 1. Ableitung der Umkehrfunktion von f(x) zu bestimmen.
Vorgehensweise:
Schritt 1: Ableiten der Funktion f(x):
f'(x) = tan²x + 1
Schritt 2: Umstellen der Funktion f(x) nach x
x = arctan(y)
Schritt 3: Einsetzen von f'(x) in g'(y)
g'(y) = 1/(tan² x + 1)
Schritt 4: Ausdruck von f'(x) durch y ersetzen
g'(y) = 1/(y² + 1)
Schritt 5: Beidseitiges Vertauschen der Variablen x und y
g'(x) = 1/(x² + 1)
Ableitung einer Kurvenschar
Kurvenscharen ableiten:
Das Ableiten von Kurvenscharen, welche einen Parameter enthalten geschieht in gleicher Weise wie das Ableiten von Funktionen. Der in einem Funktionsterm als Parameter vorkommende Wert (wie beispielsweise p oder t) wird als Konstante (c) behandelt.
Bedingungen - Extremwerte - Hochpunkt - Tiefpunkt - Wendepunkt - Sattelpunkt - Terrassenpunkt - Krümmungsverhalten - Hinreichende Bedingung - Notwendige Bedingung - Nebenbedingungen - Vorzeichenwechsel - Kriterien - Relative Extremwerte - Bestimmung - Rechnerisch
Eine notwendige Bedingung muss zwingend erfüllt sein, damit der Sachverhalt im Folgenden bestehen kann. Ist eine notwendige Bedingung nicht erfüllt, so kann der entsprechende Sachverhalt nicht eintreten. Die Bedingung ist notwendig, jedoch nicht hinreichend.
Eine hinreichende Bedingung hat in jedem Fall das Eintreten eines Sachverhalts zur Folge. Tritt die hinreichende Bedingung ein, so hat der entsprechende Sachverhalt auch einzutreten. Die Bedingung ist hinreichend, jedoch nicht notwendig. Eine hinreichende Bedingung ist eine Bedingung, die ausreichend ist, um alle Voraussetzungen zu erfüllen.
Nachfolgend wird auf hinreichende und notwendige Bedingungen für Extremwerte sowie für das Krümmungsverhalten einer Funktion eingegangen. Erste Ableitungen tragen hierbei die Bezeichnung f' (sprich f Strich), zweite Ableitungen tragen die Bezeichnung f' (sprich f zwei Strich) usw. Das Krümmungsverhalten beschreibt die Änderung der Steigung einer Funktion.
Zur Bestimmung der Extremwerte werden die erste sowie die zweite Ableitung einer Funktion benötigt. Als notwendige Bedingung für das Vorhandensein des Extremwerts einer Funktion muss der Funktionswert der ersten Ableitung an dieser Stelle gleich Null sein.
Die 1. Ableitung (erste Ableitung) beschreibt die Steigung des Graphen einer Funktion f(x) in einem Punkt.
Die 2. Ableitung (zweite Ableitung) f''(x) der Funktion beschreibt das Monotonieverhalten derer ersten Ableitung f(x) und bestimmt das Krümmungsverhalten der Kurve.
Die 3. Ableitung (dritte Ableitung) einer Funktion an einer Stelle x0 gibt Auskunft über den Wechsel des Krümmungsverhaltens des Graphen einer Funktion an dieser Stelle.
Zur Bestimmung der Wendepunkte einer Funktion werden die erste, die zweite sowie die dritte Ableitung benötigt. Hinweis: Bei Bildung der Ableitung einer Betragsfunktion sind Intervalle (Teilfunktionen) festzulegen, welche den Ausschluss nicht differenzierbarer Stellen gewährleisten.
Relative Extremwerte: Eine Funktion f(x) verfügt an der Stelle x0 über ein relatives Maximum, wenn die Bedingungen f(x0) > f(x) und x ≠ x0 erfüllt sind. Sie besitzt an der Stelle x0 ein relatives Minimum, wenn die Bedingungen f(x0) < f(x) und x ≠ x0 erfüllt sind.
Notwendige Bedingungen (Kriterien) für einen Hochpunkt (ein lokales Maximum):
- Erste Ableitung gleich Null
- Zweite Ableitung kleiner Null (negativ)
f′(x0) = 0 und f′′(x0) < 0
Vorzeichenwechselkriterium (VZW):
Ist der Funktionswert einer ersten Ableitung an einer bestimmten Stelle einer Funktion gleich 0 ist und verfügt diese Ableitungsfunktion über einen Vorzeichenwechsel von Minus nach Plus, so besitzt diese Ausgangsfunktion an dieser Stelle ein Maximum.
Notwendige Bedingungen (Kriterien) für einen Tiefpunkt (ein lokales Minimum):
- Erste Ableitung gleich Null
- Zweite Ableitung größer Null (positiv)
f′(x0) = 0 und f′′(x0) > 0
Vorzeichenwechselkriterium (VZW):
Ist der Funktionswert einer ersten Ableitung an einer bestimmten Stelle einer Funktion gleich 0 ist und verfügt diese Ableitungsfunktion über einen Vorzeichenwechsel von Plus nach Minus, so besitzt diese Ausgangsfunktion an dieser Stelle ein Maximum.
Notwendige Bedingungen (Kriterien) für einen Wendepunkt:
- Zweite Ableitung gleich Null
- Dritte Ableitung nicht gleich Null
f′′(x0) = 0
f′′′(x0) ≠ 0
Notwendige Bedingungen (Kriterien) für einen Sattelpunkt:
- Erste Ableitung gleich Null
- Zweite Ableitung gleich Null
- Dritte Ableitung nicht gleich Null
f′(x0) = 0
f′′(x0) = 0
f′′′(x0) ≠ 0
Notwendige Bedingungen (Kriterien) für einen Terrassenpunkt:
- Zweite Ableitung gleich Null
- Dritte Ableitung gleich Null
- Vierte Ableitung nicht gleich Null
f′′(x0) = 0
f′′(x0) = 0
f′''(x0) ≠ 0
Die Krümmung einer zweifach differenzierbaren Funktion kann durch die Bildung derer zweiten Ableitung ermittelt werden. Es wird zwischen keiner Krümmung, einer Linkskrümmung und einer Rechtskrümmung unterschieden.
Krümmungsverhalten (Krümmungswechsel):
Für f′′(x) < 0 gilt: Rechtsgekrümmt bzw. konkav (negative Krümmung). Nimmt die Steigung der Kurventangente beim Durchgang durch den Punkt P ab, so besitzt sie in diesem Punkt eine Rechtskrümmung.
Für f′′(x) > 0 gilt: Linksgekrümmt bzw. konvex (positive Krümmung). Nimmt die Steigung der Kurventangente beim Durchgang durch den Punkt P zu, so besitzt sie in diesem Punkt eine Linkskrümmung.
Bedingungen zur Durchführung einer Kurvendiskussion:
Nachfolgend aufgeführt ist eine Zusammenstellung der Bedingungen zur Durchführung einer Kurvendiskussion:
| Graph | Kurvenverlauf in Punkt P | Bedingung für 1. Ableitung f'(x) | Bedingung für 2. Ableitung f''(x) |
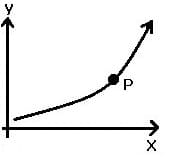 | steigend konkav | > 0 | > 0 |
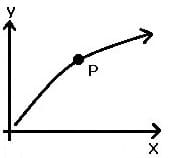 | steigend konvex | > 0 | < 0 |
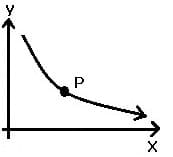 | fallend konkav | < 0 | > 0 |
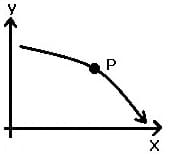 | fallend konvex | < 0 | < 0 |
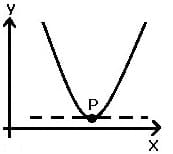 | Minimum | = 0 | > 0 |
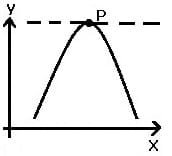 | Maximum | = 0 | < 0 |
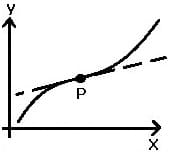 | steigend mit Wendepunkt | > 0 | = 0 |
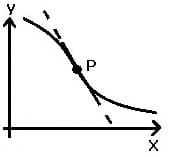 | fallend mit Wendepunkt | < 0 | = 0 |
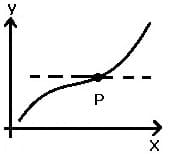 | Wendepunkt mit waagerechter Tangente | = 0 | = 0 |
Höhere Ableitungen - Ableitungen höherer Ordnung - Ableitungen höheren Grades
Höhere Ableitungen werden durch das weitere Differenzieren untergeordneter Ableitungen gebildet. Die zweite Ableitung entsteht durch das Differenzieren der ersten Ableitung. Die dritte Ableitung resultiert aus dem Differenzieren der zweiten Ableitung.
Definitionen höherer Ableitungen:
Funktion:
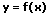
1. Ableitung:
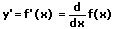
2. Ableitung:
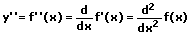
3. Ableitung:
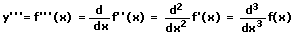
n-te Ableitung:
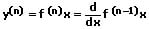
Partielle Ableitungen - Partielle Differentiation - Partielles Ableiten - Partiell differenzieren
Partielle Ableitungen werden von Funktionen gebildet, welche von mehreren Variablen abhängen. Hierbei gelten die üblichen Ableitungsregeln. Das Bilden partieller Ableitungen wird als partielle Differentiation oder partielles Ableiten bezeichnet. Als Beispiel zur Durchführung des partiellen Ableitens wird im Weiteren eine Funktion der Form f(x,y) verwendet. Nachfolgend Geschildertes bezieht sich auf derartige Funktionen.
Partielle Ableitungen 1. Ordnung
1. partielle Ableitung nach x:
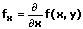
1. partielle Ableitung nach y:
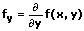
Partielle Ableitungen 2. Ordnung
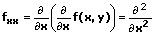
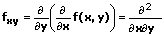
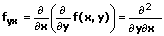
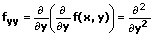
Beispiel:
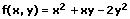
1. partielle Ableitung nach x:
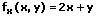
1. partielle Ableitung nach y:
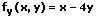
2. partielle Ableitungen:
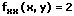
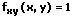
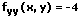
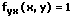
Monononie - Monotonieverhalten - Monotoniekriterium - Monotonieeigenschaften
Unter der Monotonie bzw. dem Monotonieverhalten einer Funktion wird das Steigungsverhalten der Funktion verstanden. Das Monotonieverhalten einer Funktion kann innerhalb eines Intervalls ihres Definitionsbereichs wie folgt klassifiziert werden:
f'(x) > 0: Streng monoton steigend (streng monoton wachsend)
Die Funktion verläuft im entsprechenden Intervall durchgehend steigend sowie niemals horizontal oder fallend. f(x1) ≤ f(x2) für x1 < x2.
f'(x) < 0: Streng monoton fallend
Die Funktion verläuft im entsprechenden Intervall durchgehend fallend sowie niemals horizontal oder steigend.f(x1) ≥ f(x2) für x1 < x2.
f'(x) ≥ 0: Monoton steigend (monoton wachsend)
Die Funktion verläuft im entsprechenden Intervall teilweise horizontal sowie teilweise steigend.
f'(x) ≤ 0: Monoton fallend
Die Funktion verläuft im entsprechenden Intervall teilweise horizontal sowie teilweise fallend.
Logarithmisches Differenzieren - Logarithmische Ableitung - Substitution - Substitutionsverfahren - Substitutionsmethode
Die Durchführung der logarithmischen Differentiation findet beim Bilden der Ableitung einer Funktion der Form f(x) = xx mit x > 0 Anwendung, denn es existiert keine Ableitungsregel, mit der eine derartige Funktion differenziert werden kann. Daher findet bei einem derartig vorliegenden Fall das Substituieren Anwendung. Die nachfolgend gezeigte Vorgehensweise zur Durchführung der Substitution wird als Substitutionsverfahren bzw. Substitutionsmethode bezeichnet. Die logarithmische Differentiation (bzw. logarithmisches Differenzieren) kann wie nachfolgend beschrieben praktiziert werden.
Gegeben sei folgende Funktion:
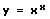
Um die erste Ableitung der zuvor gezeigten Funktion zu bestimmen, sind die im Folgenden gezeigten Schritte auszuführen.
Schritt 1 - Logarithmieren
der beiden Gleichungsseiten
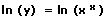
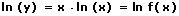
Es gilt zu beachten, dass sich der Definitionsbereich der Funktion hierbei ändern kann!
Schritt 2 - Substituieren
mit:
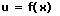
Schritt 3 - Ableiten
mit Hilfe der Kettenregel:
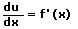
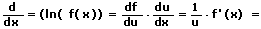
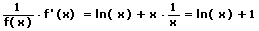
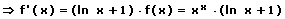
Eine Ableitung dieser Art wird als logarithmische Ableitung bezeichnet.
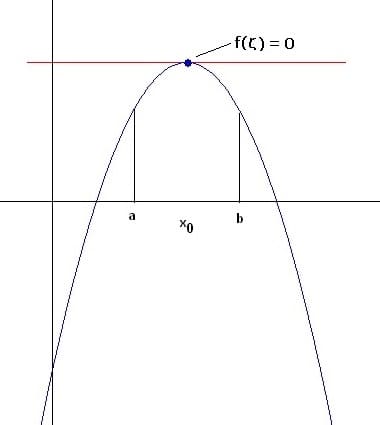
Satz von Rolle:
Ist f im Intervall <a,b> stetig und in (a,b) differenzierbar und ist f(a) = f(b), so existiert mindestens eine Stelle ς mit a < ς < b, so dass gilt: f'(ς) = 0. Geometrisch gedeutet besagt dieser Satz, dass es im Intervall <a,b> mindestens einen Punkt mit einer zur x-Achse parallelen Tangente gibt.
Differentialgeometrie:
Die Differentialgeometrie untersucht Kurven und Fläche mit Hilfe der Differentialrechnung. Jeder stetigen Funktion entspricht eine stetige Kurve. Jeder differenzierbaren Funktion entspricht eine glatte Kurve (ohne Unstetigkeiten etc.).
Verallgemeinerter Mittelwertsatz:
Sind zwei Funktionen f und g im Intervall <a,b> stetig und im Intervall (a,b) differenzierbar, so gibt es mindestens eine Zahl ς mit a < ς < b, so dass gilt:
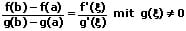
Infinitesimalrechnung:
Die Infinitesimalrechnung ist eine von Gottfried Wilhelm Leibniz (1646 - 1716) und Isaac Newton (1642 - 1727) unabhängig voneinander entwickelte Methode, welche als zusammenfassende Bezeichnung der Differenzialrechnung und der Integralrechnung verwendet wird. Hierbei wird mit beliebig kleinen Größen gerechnet. Die Infinitesimalrechnung beschreibt eine mathematische Funktion auf unendlich kleinen Abschnitten. Ihre Umkehrung ist die Integralrechnung.
Als Extremwertaufgaben oder Extremalprobleme (Extremwertprobleme) werden Aufgaben bezeichnet, bei welchen es gilt, den größten bzw. den kleinsten Extremwert einer Funktion der Form f(x) innerhalb eines bestimmten Intervalls (oder seiner Randpunkte) zu ermitteln. Hierbei wird das absolute Maximum bzw. Minimum dieser Funktion gesucht.
Mit der Durchführung einer Kurvendiskussion im vorgegebenen Intervall werden relative Maxima oder Minima der zu untersuchenden Funktion ermittelt. Durch den Vergleich dieser Funktionswerte mit den Randpunkten des festgelegten Intervalls wird der gesuchte und sich darin befindende größte bzw. kleinste Wert festgestellt.

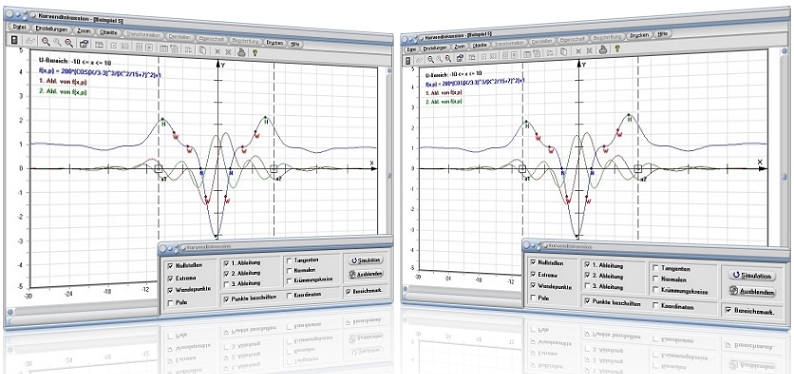
Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2
Die Durchführung einer Kurvendiskussion (Funktionsuntersuchung und Differentialrechnung) mit einer explizit definierten Funktion der Form f(x,p) können Sie veranlassen, indem Sie Folgendes ausführen:
- Definieren Sie die Funktion, gemäß den geltenden Syntaxregeln, im Eingabefeld mit der Bezeichnung f(x,p) =.
- Legen Sie durch die Eingabe entsprechender Zahlenwerte den Untersuchungsbereich fest, innerhalb dessen die Analyse durchgeführt werden soll (Untersuchungsbereich von x1 = und bis x2 =).
- Durch die Wahl des Kontrollschalters Grob, Mittel, Fein oder Sehr fein legen Sie die zu verwendende Untersuchungsgenauigkeit zur Ermittlung von Nullstellen, Extrema und Wendepunkten fest.
- Nach einer Bedienung der Schaltfläche Berechnen werden die Untersuchungen durchgeführt und deren Ergebnisse ausgegeben.
Hierauf werden, durch die Fokussierung der entsprechenden Tabelleneinträge, die weiteren, dem entsprechenden Punkt zugehörigen Eigenschaften u. dgl. (z.B. Steigung, Tangente usw.) in der darunter angeordneten Liste ausgegeben.
- Möchten Sie sich die Zusammenhänge grafisch veranschaulichen, so bedienen Sie danach die Schaltfläche Darstellen.
- Bestimmen Sie den zu analysierenden Bereich, indem Sie in die entsprechenden, rechteckig umrahmten Mausfangbereiche klicken und bewegen Sie den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts (je schmaler der Bereich gewählt wird, desto exakter sind die resultierenden Berechnungsergebnisse).
- Wählen Sie auf dem Bedienformular durch Aktivierung des Kontrollkästchens Nullstellen, Extrema, Wendepunkte bzw. Pole, ob ermittelte Nullstellen, Extrema, Wendepunkte bzw. Pole der Funktion angezeigt werden sollen.
- Legen Sie durch die Aktivierung/Deaktivierung der Kontrollkästchen 1. Ableitung, 2. Ableitung, 3. Ableitung fest, ob die Darstellung der 1. Ableitung, 2. Ableitung oder 3. Ableitung der Funktion ausgegeben werden soll.
- Möchten Sie sich ggf. die Tangenten oder Normalen, die durch Hoch-, Tief- und Wendepunkte der Funktion verlaufen, zeigen lassen, so aktivieren Sie hierfür das entsprechende Kontrollkästchen Tangenten bzw. Normalen. Um sich Krümmungskreise darstellen zu lassen, die durch Nullstellen oder Extrema (Extrempunkte) verlaufen, aktivieren Sie das Kontrollkästchen Krümmungskreise.
- Sollen die Bereichsgrenzen zur Untersuchung der Funktion mit der Maus verändert werden, so klicken Sie mit der linken Maustaste in den rechteckig umrahmten Mausfangbereich und bewegen den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts.
- Enthält der Funktionsterm das Einzelzeichen P, so legen Sie, wie unter Verwendung von Funktionsparametern beschrieben, nach einer Bedienung des Schalters Parameter P den zu durchlaufenden Wertebereich für diesen Funktionsparameter, sowie die zu verwendende Schrittweite, fest. Positionieren Sie hierauf den Schieberegler Parameter P, um den Einfluss des Parameters P zu untersuchen.
- Möchten Sie Analysen mit Hilfe von Simulationen durchführen, so wählen Sie durch Aktivierung des Kontrollschalters Bereich oder Parameter P die Art der Simulation die Sie ausführen lassen möchten.
Um Untersuchungspositionen simulativ verändern, oder eine automatisch ablaufende Parameterwertsimulation durchführen zu lassen, klicken Sie auf die Schaltfläche Simulation.
Vor Ausführung einer Simulation des Untersuchungsbereichs wird Ihnen ein Formular zur Verfügung gestellt auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Bestätigen Sie mit OK.
Beendet werden kann die Ausführung einer Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
Hinweise:
Die Genauigkeit der Berechnungsergebnisse hängt u.a. davon ab, innerhalb welchem Untersuchungsbereich die Analyse durchgeführt wird, wie auch davon welche Genauigkeit zur Durchführung der Berechnungen festgelegt wurde. Diese kann durch die Fokussierung eines Kontrollschalters Grob, Mittel, Fein oder Sehr fein vorgegeben werden.
Nicht in jedem Fall ist eine eindeutige Bestimmung aller evtl. vorhandener Punkte innerhalb des gewählten Untersuchungsbereichs einer Kurve möglich. Voraussetzung ist zudem die Differenzierbarkeit einer definierten Funktion. Somit kann es vorkommen, dass insbesondere Nullstellen und Wendepunkte nicht ermittelt werden können. Dies kann u.a. bei der Analyse von Kurven auftreten, bei welchen sich viele eng beieinander liegende Stellen dieser Art befinden. Auch kann dies bei der Analyse von Kurven auftreten, bei welchen an einer Nullstelle kein Vorzeichenwechsel stattfindet.
Um Krümmungskreise nicht oval (ellipsenförmig) dargestellt zu bekommen, wählen Sie bei Ausgabe der grafischen Darstellung den Menüpunkt Einstellungen - Auflösung - Skalierungsart - Linear.
Bei der Ausgabe ermittelter Punkte auf dem Formular werden folgende Bezeichnungskürzel verwendet:
| N | Nullstelle |
| HP | Hochpunkt (Maximum) |
| TP | Tiefpunkt (Minimum) |
| W | Wendepunkt (Wendestelle) |
| M | Mittelpunkt des Krümmungskreises |
Bei grafischen Darstellungen haben diese folgende Bedeutungen:
| N | Nullstelle |
| H | Hochpunkt (Maximum) |
| T | Tiefpunkt (Minimum) |
| W | Wendepunkt (Wendestelle) |
| KM | Mittelpunkt des Krümmungskreises |
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformulare
Wurde zur Durchführung einer Kurvendiskussion ein Funktionsterm erstellt, der kein Einzelzeichen P zur Definition eines Funktionsparameters enthält, so wird bei der Ausgabe einer grafischen Darstellung nachfolgend gezeigtes Bedienformular zur Verfügung gestellt.

Enthält der erstellte Term das Einzelzeichen P zur Definition eines Funktionsparameters, so wird bei der Ausgabe einer grafischen Darstellung das nachfolgend abgebildete Formular eingeblendet.

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollschalter / Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
- Bereichsmark.: Markierung des Untersuchungsbereichs ein-/ausschalten
- Punkte beschriften: Beschriftung ermittelter Nullstellen, Extrema (Extrempunkte), Wendepunkte und Krümmungskreis-Mittelpunkte ein-/ausschalten
- Koordinaten: Koordinatenwertanzeige ermittelter Nullstellen, Extrema (Extrempunkte), Wendepunkte und Krümmungskreis-Mittelpunkte ein-/ausschalten
Analytische Ermittlung von Ableitungen
Unter dem Menüpunkt Ableitungen analytisch können Sie sich die 1. und 2. Ableitung der definierten Funktion f(x) symbolisch differenziert ausgeben lassen. Es erscheint ein Formular.
- Definieren Sie die Funktion, gemäß den geltenden Syntaxregeln, im Eingabefeld mit der Bezeichnung Y = f(x) =. Der definierte Funktionsterm darf nicht das Einzelzeichen P enthalten!
- Nach der korrekten Deklaration der Funktion im Eingabefeld und der Bedienung des Schalters Berechnen wird die 1. und 2. Ableitung der eingegebenen Funktion ermittelt und in den entsprechenden Ausgabefeldern angezeigt.
Ist die Funktionsdeklaration zu komplex um eine Ableitung symbolisch differenzieren zu können, so erscheint der Eintrag 'Funktion zu komplex - nicht differenzierbar' in den Ausgabefeldern.
Durch die Bedienung der dortigen Schaltfläche Schließen, kehren Sie wieder zum Hauptformular des Unterprogramms zurück.
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Beispiel - Aufgabe
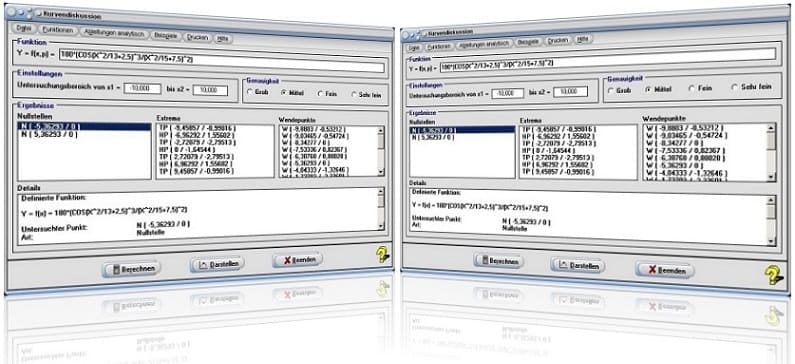
Es gilt, die Funktion f(x) = sin(x-2)+0,5 innerhalb eines Bereichs -2 ≤ x ≤ 2 auf Nullstellen, Extremwerte (Maxima und Minima) und Wendepunkte (Wendestellen) untersuchen zu lassen.
Vorgehensweise und Lösung:
Nach der Definition des Funktionsterms SIN(X-2)+0,5 im Eingabefeld f(x) =, der Festlegung eines Untersuchungsbereichs von -2 ≤ x ≤ 2 durch die Eingabe der entsprechenden Zahlenwerte in die dafür zur Verfügung stehenden Felder, ermittelt das Programm bei einer eingestellten Genauigkeit vom Grad Mittel nach einer Bedienung der Schaltfläche Berechnen Folgendes:
Die Funktion besitzt innerhalb des gewählten Untersuchungsbereichs:
| Nullstellen: | N (-0,61799 / 0) | N (1,4764 / 0) |
| Extrema (Extrempunkte): | TP (0,4292 / -0,5) | |
| Wendepunkte (Wendestellen): | W (-1,14159 / 0,5) | W (2 / 0,5) |
Zudem werden bei einer Fokussierung des obersten Eintrags der Tabelle Nullstellen bzgl. der Eigenschaften der Funktion und der entsprechenden Nullstelle N (-0,61799 / 0) folgende Resultate in der darunter angeordneten Tabelle ausgegeben:
| Steigung in Punkt N: | m = -0,86602 |
| Gleichung der Tangente in Punkt N: | Y = -0,86602·X - 0,5352 |
| Gleichung der Normale in Punkt N: | Y = 1,1547·X + 0,7136 |
| Mittelpunkt des Krümmungkreises durch Punkt N: | M (2,401303 / 3,49993) |
| Radius des Krümmungkreises durch Punkt N: | r = 4,62997 |
| Krümmung in Punkt N: | kr = 0,216 (konkav) |
| Funktionseigenschaft: | unsymmetrisch |
| Schnittpunkt der Funktion mit y-Achse: | Y = -0,4093 |
Bei der Fokussierung des obersten Eintrags der Tabelle Extrema werden bzgl. der mathematischen Eigenschaften der Funktion und des entsprechenden Tiefpunkts T (0,4292 / -0,5) folgende Resultate in der darunter angeordneten Tabelle ausgegeben:
| Steigung in Punkt T: | m = 0 |
| Gleichung der Tangente in Punkt T: | Y = -0,5 |
| Gleichung der Normale in Punkt T: | X = 0,4292 |
| Mittelpunkt des Krümmungkreises durch Punkt T: | M (0,4292 / 0,5) |
| Radius des Krümmungkreises durch Punkt T: | r = 1 |
| Krümmung in Punkt T: | kr = 1 (konkav) |
| Funktionseigenschaft: | unsymmetrisch |
| Schnittpunkt der Funktion mit y-Achse: | Y = -0,4093 |

Grafische Darstellung - Beispiel 3

Grafische Darstellung - Beispiel 4

Grafische Darstellung - Beispiel 5

Grafische Darstellung - Beispiel 6

Grafische Darstellung - Beispiel 7

Grafische Darstellung - Beispiel 8

Grafische Darstellung - Beispiel 9

Grafische Darstellung - Beispiel 10
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Kurvendiskussion
Wikipedia - Differentialrechnung
Wikipedia - Tangente
Wikipedia - Ableitung
Wikipedia - Nullstelle
Wikipedia - Extremwert
Wikipedia - Krümmung
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form -Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
Startfenster des Unterprogramms Kurvendiskussion
MathProf 5.0 - Unterprogramm Tangente durch Punkt

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.