PhysProf - Regressionsanalyse - Regressionsmodell - Korrelationsanalyse
Fachthema: Regressionsanalyse
PhysProf - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.
Online-Hilfe für das Modul
zur Durchführung von Regressionsanalysen mit Hilfe verschiedener Regressionsmodelle zur Berechnung der entsprechenden Korrelation.
Mit Hilfe dieses Moduls wird es ermöglicht, einfache Regressionsanalysen mit verschiedenen grundlegenden Regressionsmodellen zu praktizieren.
Nach einer Defintion der zu untersuchenden Wertepaare und einer Wahl des zu analysierenden Modells ermittelt das Programm die Funktionsgleichung für das entsprechende Modell im vorliegenden Fall und gibt den hierzu gehörenden Wert für den zugehörigen Korrelationskoeffizienten aus.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul: |
 |  |
Regressionsanalyse
Durch die Benutzung des Unterprogramms [Allgemeines] - [Regressionsanalyse] können Regressionsanalysen mit verschiedenen Modellen durchgeführt werden.
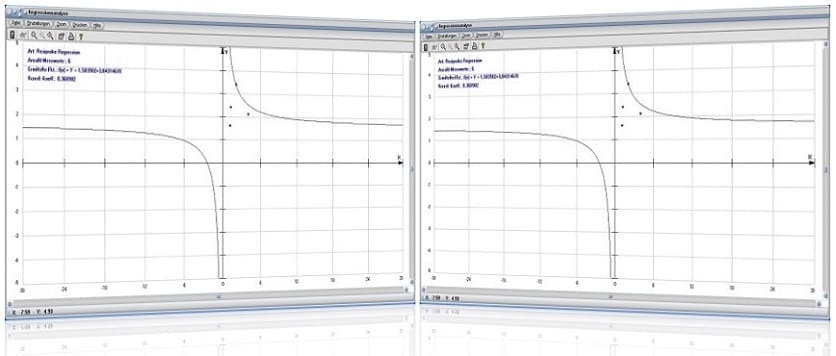
Regressionsanalyse - Abbildung 1
Regressionsanalyse - Abbildung 2
Unter Zuhilfenahme der Regressionsanalyse kann ein vermuteter Zusammenhang daraufhin überprüft werden, ob er mit ermittelten Daten konsistent ist.
Bei einem linearen Zusammenhang kann hierbei ermittelt werden, welche Werte für die Parameter M und N einer Geraden der Form Y = M·X+N erforderlich sind, um diesen bestens zu beschreiben.
Mitunter kann durch eine grafische Veranschaulichung geprüft werden, ob die Daten mit der Annahme eines linearen Zusammenhangs konsistent sind, oder ob signifikante Abweichungen vorhanden sind. Da in der Praxis aber vermehrt die Analyse nichtlinearer Zusammenhänge erforderlich ist, ist auch die Durchführung einiger dieser mit diesem Programm möglich.
Es kann hierbei eine Zielfunktion der nachfolgend aufgeführter Arten ausgewählt werden:
- Logarithmische Regression Y = A+B·LN(X)
- Geometrische Regression Y = A·X^B
- Reziproke Regression Y = A+B/X
- Exponentielle Regression Y = A·B^X
- Trigonometrische Regression Y = A+B·SIN(X)
Bei Auswahl der entsprechenden Methode gilt es Folgendes zu beachten:
| - Logarithmische Regression: | Alle X-Werte müssen > 0 sein |
| - Geometrische Regression: | Alle X-Werte und alle Y-Werte müssen > 0 sein |
| - Reziproke Regression: | Kein X-Wert darf 0 sein |
| - Exponentielle Regression: | Alle Y-Werte müssen > 0 sein |
Zudem wird der Korrelationskoeffizient ermittelt, welcher Auskunft über die Qualität des Zusammenhangs der Messgrößen gibt.
Berechnung und grafische Darstellung
Führen Sie Folgendes aus, um eine Regressionsanalyse mit Datenpaaren von Messwertreihen durchführen zu lassen:
-
Wählen Sie zunächst im Formularbereich Regressionsart die Art aus, mit welcher Sie eine Analyse durchführen möchten.
-
Geben Sie die auszuwertenden Messdaten in die dafür vorgesehenen Felder X und Y ein, bedienen Sie die Schaltfläche Übernehmen und wiederholen Sie diesen Vorgang, bis alle erforderlichen Messwerte aufgenommen sind.
-
Möchten Sie einen Eintrag in der Tabelle löschen, so fokussieren Sie diesen und bedienen die Schaltfläche Löschen. Soll ein bereits eingetragener Wert geändert werden, so fokussieren Sie zunächst den entsprechenden Eintrag in der Tabelle, geben den neuen Wert in das Feld ein und bedienen hierauf die Schaltfläche Ersetzen. Um alle Einträge zu löschen, kann die Schaltfläche Alle löschen verwendet werden.
-
Bedienen Sie die Schaltfläche Berechnen.
-
Um sich die Verteilung der Messwerte, sowie den Verlauf der ermittelten Regressionsfunktion grafisch zu veranschaulichen, bedienen Sie die Schaltfläche Darstellen.
Hinweise:
Die Anzahl eingegebener X-Werte muss mit der Anzahl eingegebener Y-Werte übereinstimmen, bevor die Durchführung einer Berechnung, bzw. die Ausgabe einer grafischen Darstellung ermöglicht wird. Zudem muss hierfür eine Mindestanzahl von 3 Datenwertpaaren definiert sein.
Allgemein
Möchten Sie eingegebene Messwerte speichern, so kann dies über den Menüeintrag Datei - Speichern durchgeführt werden. Um mit bereits gespeicherten Daten eine Analyse durchzuführen, verwenden Sie den Menüeintrag Datei - Öffnen. Die Befehle Öffnen und Speichern werden stets mit der Datenmenge ausgeführt, deren Kontrollschalter aktiviert ist. Beim Öffnen einer Datei werden bereits eingegebene Werte durch die Dateidaten überschrieben!
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Beispiel
Es ist eine Analyse folgender Messwertpaare durchzuführen:
| X -Wert | Y-Wert |
| 4,1 | 2,1 |
| 1,3 | 2,4 |
| 1,2 | 1,6 |
| 1,5 | 7,4 |
| 1,1 | 7,5 |
| 2,2 | 3,4 |
Nach Eingabe der Daten in die Tabelle, der aufeinanderfolgenden Selektion der entsprechenden Einträge aus der Tabelle Regressionsart und anschließender Durchführung der Berechnungen wird ausgegeben:
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Notizen - Taschenrechner - Fachbegriffe Deutsch - Englisch - Materialkonstanten - Physikalische Größen - Maßeinheiten - Naturkonstanten - Physiker - Nobelpreisträger - Periodensystem der Elemente - Messwertreihen - Statistische Messwertanalyse - Zusammenhang von Messwerten - Vektoraddition - Vektorprojektion
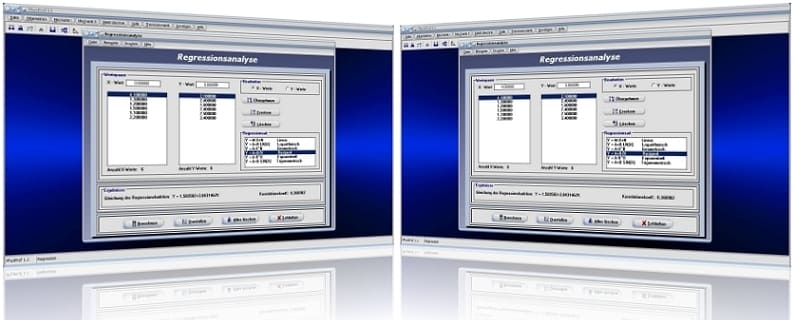
Unterprogramm Regressionsanalyse
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
