MathProf - Rechtwinklige Dreiecke - Dreieck berechnen - Försterdreieck

Fachthema: Rechtwinklige Dreiecke - Försterdreieck
MathProf - Trigonometrie - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Praktizierung interaktiver grafischer Analysen mit rechtwinkligen Dreiecken.
Dieses Teilprogramm ermöglicht neben der Durchführung der entsprechenden Dreieckskonstruktion unter anderem das Berechnen der Werte folgender Eigenschaften des rechtwinkligen Dreiecks: Umkreis des Dreiecks, Inkreis des Dreiecks, Ankreise des Dreiecks, Seitenlängen des Dreiecks, Höhe des Dreiecks, Winkelhalbierende des Dreiecks, Seitenhalbierende des Dreiecks, Mittelsenkrechten des Dreiecks.
Zudem ermittelt das Programm: Flächeninhalt des Dreiecks, Ankathete des Dreiecks, Gegenkathete des Dreiecks, Hypotenuse des Dreiecks, Hypotenusenabschnitte des Dreiecks, Innenwinkel des Dreiecks und Flächenschwerpunkt des Dreiecks.
Die Ausgabe der Werte ermittelter Größen erfolgt zur Echtzeit. Der Rechner stellt die entsprechenden Zusammenhänge unmittelbar nach Eintritt einer interaktiven Operation dar. Jedes relevante Ergebnis einer durchgeführten Berechnung zu diesem Fachthema wird aktualisiert ausgegeben.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Rechtwinklige Dreiecke - Försterdreieck - Fläche des rechtwinkligen Dreiecks - Winkel des rechtwinkligen Dreiecks - Seiten des rechtwinkligen Dreiecks - Seitenhalbierende - Winkelhalbierende - Höhe eines Dreiecks - Seitenlängen des rechtwinkligen Dreiecks - Dreieckshöhe - Mittelsenkrechte - Ankathete - Gegenkathete - Hypotenuse - Inkreis - Inkreismittelpunkt - Ankreise - Schwerpunkt eines rechtwinkligen Dreiecks - Hypotenusenabschnitt p - Hypotenusenabschnitt q - Flächenschwerpunkt eines rechtwinkligen Dreiecks - Seitenhalbierende eines rechtwinkligen Dreiecks - Winkelhalbierende eines rechtwinkligen Dreiecks - Mittelsenkrechte eines rechtwinkligen Dreiecks - Außenkreis des rechtwinkligen Dreiecks - Rechtwinkliges gleichschenkliges Dreieck - Rechtwinkliges gleichseitiges Dreieck - Umkreis des rechtwinkligen Dreiecks - Winkelberechnung am rechtwinkligen Dreieck - Dreiecksberechnung - Dreieckskonstruktion - Trigonometrische Berechnungen - Berechnen der Dreieckshöhe - Berechnen der Dreiecksfläche - Geometrische Eigenschaften - Außenkreis - Innenkreis - Flächeninhalte - Schwerlinien - Grafik - Untersuchen - Untersuchung - Grafisch - Rechner - Berechnen - Berechnung - Graph - Plot - Darstellen - Präsentation - Dreiecksseiten - Seite berechnen - Seitenberechnung am Dreieck - Mittelpunkt des Inkreises eines Dreiecks |
Rechtwinkliges Dreieck - Interaktiv
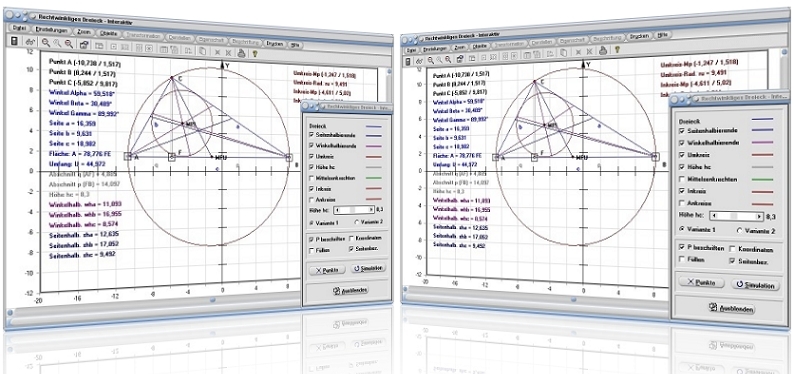
Modul Rechtwinkliges Dreieck - Interaktiv
Mit dem Unterprogramm [Trigonometrie] - Rechtwinkliges Dreieck - Interaktiv können die Eigenschaften eines rechtwinkligen Dreiecks interaktiv analysiert werden.

Wesentliche Eigenschaften des rechtwinkligen Dreiecks:
- Die Hypotenuse eines rechtwinkligen Dreiecks ist grundsätzlich die längste Seite im Dreieck
- Auf rechtwinklige Dreiecke lässt sich der Satz des Pythagoras anwenden
- Die Katheten (Ankathete und Gegenkathete) rechtwinkliger Dreiecke sind gleichzeitig die Höhen der zwei Eckpunkte an der Hypotenuse
- Der Mittelpunkt der Hypotenuse des rechtwinkligen Dreiecks ist der Mittelpunkt des Thaleskreises
- Punkt B des rechtwinkligen Dreiecks befindet auf dem Thaleskreis
Nach der Wahl dieses Programmpunkts wird ein vordefiniertes, rechtwinkliges Dreieck grafisch dargestellt, dessen Eigenschaften Sie ändern können. Hierzu haben Sie zwei Möglichkeiten:
- Anklicken eines Punktes des Dreiecks mit der linken Maustaste und Bewegung der Maus bei gedrückt gehaltener Maustaste.
- Bedienung der Schaltfläche Punkte und der Eingabe gewünschter Werte zur Darstellung des Dreiecks in dem daraufhin erscheinenden Formular. Nach einem Klick auf die Schaltfläche Ok wird das Dreieck mit den vorgegebenen geometrischen Eigenschaften dargestellt.
Berechnung und Darstellung
Es bestehen zwei verschiedene Möglichkeiten die Eigenschaften des dargestellten Dreiecks interaktiv zu verändern. Das Programm stellt in beiden Fällen stets ein rechtwinkliges Dreieck dar.
- Variante 1:
Sie können die Eckpunkte des Dreiecks anfassen und innerhalb des Darstellungsbereichs an beliebige Positionen verschieben.
- Variante 2:
Sie können die Hypotenuseneckpunkte, sowie den Höhenfußpunkt des Dreiecks anfassen, verschieben und die Höhe des Dreiecks durch die entsprechende Positionierung des Rollbalkens Höhe h einstellen.
Eine Auswahl bzgl. der zu verwendenden Variante treffen Sie durch die Aktivierung des Kontrollschalters Variante 1 bzw. Variante 2.
Es werden nachfolgend aufgeführte Werte für Größen des dargestellten Dreiecks ausgegeben und bei jeder Änderung der Koordinatenwerte der Eckpunkte des Dreiecks aktualisiert:
- Punktkoordinaten des Dreiecks (Punkte A, B, C)
- Höhe hc bzw. ha des Dreiecks
- Seitenhalbierende sha, shb, shc des Dreiecks
- Winkelhalbierende wha, whb, whc des Dreiecks
- Umkreis: Umkreisradius ru und Umkreismittelpunkt MPu des Dreiecks
- Inkreis: Inkreisradius ri und Inkreismittelpunkt MPi des Dreiecks
- Seitenlängen a, b, c des Dreiecks
- Innenwinkel des Dreiecks (Winkel BAC, ABC, ACB)
- Flächeninhalt des Dreiecks
- Ankreise: Ankreisradien, Ankreismittelpunkte des Dreiecks
- Abschnitte p und q des Dreiecks
Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. die Werte für Schrittweite, Verzögerung bzw. die Anzahl zu verwendender Winkelschritte einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Simulation wieder durch eine Bedienung der Schaltfläche Sim. Stop.
Hinweis:
Um sich die weitere Informationen bzgl. der geometrischen Eigenschaften des Dreiecks ABC ausgeben zu lassen, wählen Sie den Menüpunkt Datei - Dreieckseigenschaften. Hierauf erscheint ein Ausgabefenster mit den relevanten Daten. Um diese im *.txt-Format zu speichern, verwenden Sie den dort vorhandenden Menüeintrag Datei - Ergebnisse speichern.
Mit Hilfe des Försterdreiecks ist es möglich, die Höhe von vertikal positionierten Objekten wie Bäume, Türme oder ähnlichem zu bestimmen. Es wird insbesondere zur Bestimmung von Baumhöhen eingesetzt.
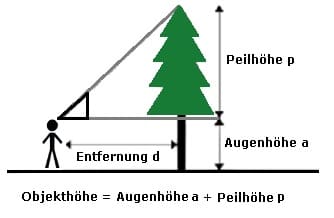
Der Standort zur Bestimmung der Höhe eines entsprechenden Objekts (Objekthöhe) wird derart festgelegt, dass der Beobachter über die Hypotenuse des rechtwinkligen Dreiecks die Spitze des Objekts anpeilen kann, wenn das Dreieck derart gehalten wird, dass eine Kathete exakt waagerecht und die andere exakt senkrecht steht (siehe Abbildung). Unter Anwendung des Strahlensatzes kann aus der Entfernung und den beiden Katheten des Dreiecks die Höhe des Objekts bestimmt werden. Hierbei gilt für das Försterdreieck:
Höhe = Entfernung + senkrechte Kathete / waagerechte Kathete · Augenhöhe
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformular
Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen.

- P beschriften: Beschriftung der Eck-, Ankreis-, Inkreis- und Umkreismittelpunkte des Dreiecks ein-/ausschalten
- Koordinaten: Anzeige der Koordinatenwerte der Eck-, Ankreis-, Inkreis- und Umkreismittelpunkte des Dreiecks ein-/ausschalten
- Füllen: Farbfüllung des Dreiecks ein-/ausschalten
- Seitenbez.: Anzeige der Seitenbezeichnungen des Dreiecks ein-/ausschalten
Außerdem wird die Ein- und Ausblendung folgender Größen ermöglicht:
- Seitenhalbierende des rechtwinkligen Dreiecks
- Winkelhalbierendedes rechtwinkligen Dreiecks
- Inkreis des rechtwinkligen Dreiecks
- Umkreis des rechtwinkligen Dreiecks
- Höhe des rechtwinkligen Dreiecks
- Mittelsenkrechten des rechtwinkligen Dreiecks
- Ankreise des rechtwinkligen Dreiecks
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Verallgemeinerung des Satz des Pythagoras
Beispiele
Beispiel - Rechtwinkliges Dreieck - Variante 1:
Wurde Kontrollschalter Variante 1 fokussiert, und positionieren Sie die Punkte B und F des Dreiecks mit den Koordinatenwerten B (-4 / 4) und F (-3 / 4), so gibt das Programm (nach Aktivierung der entsprechenden Kontrollkästchen) folgende Werte für die Eigenschaften des Dreiecks aus:
Koordinatenwerte der Eckpunkte:
Punkt A (-3 / 6,646)
Punkt B (-4 / 4)
Punkt C (4 / 4)
Sonstige Eigenschaften:
Innenwinkel: BAC = 90°
Innenwinkel: ABC = 69,295°
Innenwinkel: ACB = 20,705°
Seitenlänge: a = 8
Seitenlänge: b = 7,483
Seitenlänge: c = 2,828
Höhe: ha = 2,646
Hypotenusenabschnitt (Strecke BF): p = 1
Hypotenusenabschnitt (Strecke FC): q = 7
Länge der Winkelhalbierende auf Seite a: wha = 2,903
Länge der Winkelhalbierende auf Seite b: whb = 3,438
Länge der Winkelhalbierende auf Seite c: whc = 7,607
Länge der Seitenhalbierende auf Seite a: sha = 4
Länge der Seitenhalbierende auf Seite b: shb = 4,69
Länge der Seitenhalbierende auf Seite c: shc = 7,616
Inkreis:
Inkreisradius: ri = 1,156
Inkreismittelpunkt: MP (-2,327 / 5,156)
Umkreis:
Umkreisradius: ru = 4
Umkreismittelpunkt: MP (0 / 4)
Fläche des Dreiecks: A = 10,583 FE
Umfang des Dreiecks: U = 18,312
Ankreis auf Seite a:
Radius: ra = 9,156
Ankreismittelpunkt: MPA1 (2,327 / -5,156)
Ankreis auf Seite b:
Radius: rb = 1,673
Ankreismittelpunkt: MPA2 (-5,156 / 5,673)
Ankreis auf Seite c:
Radius: rc = 6,327
Ankreismittelpunkt: MPA3 (5,156 / 10,327)
Beispiel - Rechtwinkliges Dreieck - Variante 2:
Gilt es ein rechtwinkliges Dreieck berechnen zu lassen, dessen Eckpunktkoordinaten bekannt sind, so aktivieren Sie Kontrollschalter Variante 2. Definieren Sie die Koordinatenwerte der Punkte A (-4 / 4), B (-4 / -6) und C (8 / -6), so gibt das Programm nach Aktivierung der entsprechenden Kontrollkästchen folgende Werte für die Eigenschaften dieses rechtwinkligen Dreiecks aus:
Koordinaten der Eckpunkte:
Punkt A (-4 / 4)
Punkt B (-4 / -6)
Punkt C (8 / -6)
Sonstige Eigenschaften:
Innenwinkel: BAC = 50,194°
Innenwinkel: ABC = 90°
Innenwinkel: ACB = 39,806°
Seitenlänge: a = 12
Seitenlänge: b = 15,62
Seitenlänge: c = 10
Höhe: hb = 7,682
Hypotenusenabschnitt (Strecke CF): p = 9,219
Hypotenusenabschnitt (Strecke AF): q = 6,402
Länge der Winkelhalbierende auf Seite a: wha = 11,043
Länge der Winkelhalbierende auf Seite b: whb = 7,714
Länge der Winkelhalbierende auf Seite c: whc = 12,762
Länge der Seitenhalbierende auf Seite a: sha = 11,662
Länge der Seitenhalbierende auf Seite b: shb = 7,81
Länge der Seitenhalbierende auf Seite c: shc = 13
Inkreis:
Inkreisradius: ri = 3,19
Inkreismittelpunkt: MP (-0,81 / -2,81)
Umkreis:
Umkreisradius: ru = 7,81
Umkreismittelpunkt: MP (2 / -1)
Fläche des Dreiecks: A = 60 FE
Umfang des Dreiecks: U = 37,62
Ankreis auf Seite a:
Radius: ra = 8,81
Ankreismittelpunkt: MPA1 (4,81 / -14,81)
Ankreis auf Seite b:
Radius: rb = 6,81
Ankreismittelpunkt: MPA2 (-10,81 / 0,81)
Ankreis auf Seite c:
Radius: rc = 18,81
Ankreismittelpunkt: MPA3 (14,81 / 12,81)

Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2

Grafische Darstellung - Beispiel 3

Grafische Darstellung - Beispiel 4

Grafische Darstellung - Beispiel 5
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Rechtwinkliges Dreieck
Wikipedia - Inkreis
Wikipedia - Umkreis
Wikipedia - Ankreis
Rechtwinkliges Dreieck - Allgemeines Dreieck aus Seitenlängen und Winkeln - Allgemeines Dreieck durch 3 Punkte - Allgemeines Dreieck - Interaktiv - Satz des Pythagoras - Verallgemeinerung des Satz des Pythagoras - Satz des Thales - Höhensatz - Kathetensatz - Winkel am Dreieck - Innenwinkel des Dreiecks - Winkel am Kreis - Winkel an Parallelen - Sinus und Cosinus am Einheitskreis - Tangens und Cotangens am Einheitskreis - Tangentendreieck - Höhenfußpunktdreieck - Lamoen-Kreis - Taylor-Kreis - Euler-Gerade - Simson-Gerade - Satz von Ceva - Isodynamische Punkte des Dreiecks - Isogonal konjugierte Punkte - Spieker-Punkt - Apollonius-Punkt
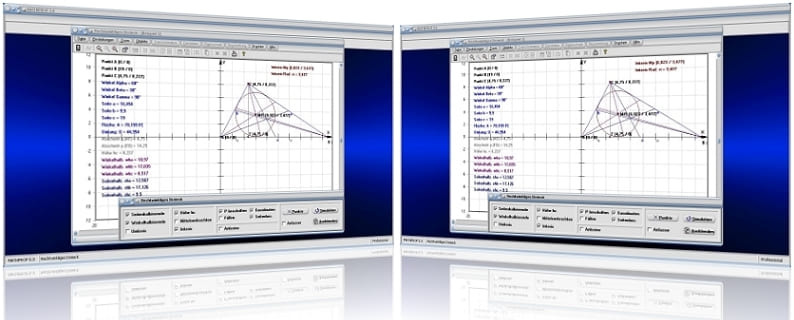
MathProf 5.0 - Unterprogramm Rechtwinkliges Dreieck

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















