Screenshots zum
Themengebiet Algebra
Nachfolgend dargestellt sind Screenshots von Beispielen
einiger zu diesem Fachthemengebiet in MathProf 5.0
implementierter Unterprogramme.
finden Sie hier, oder durch die Ausführung eines Klicks auf ein Bild.
Das Unterprogramm [Algebra] - [Matrizen] ermöglicht die Durchführung von Berechnungen mit quadratischen Matrizen reeller und komplexer Zahlen.
Im Programmteil [Algebra] - [Gauß'scher Algorithmus] kann die schrittweise Lösung eines linearen Gleichungssystems nachvollzogen werden.
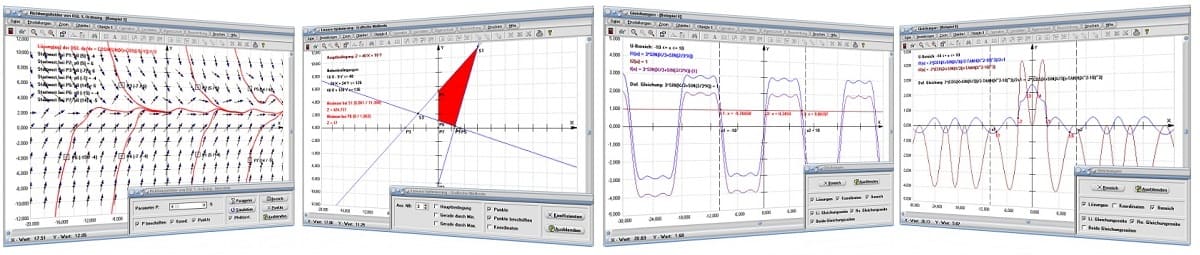
Die Verwendung des Moduls [Algebra] - [Lineare Optimierung - Simplex-Methode] ermöglicht die numerische Ermittlung der Lösungen von Optimierungsaufgaben mit Hilfe der Simplex-Methode.
Das Unterprogramm [Algebra] - [Lineare Optimierung] - [Grafische Methode] ermöglicht die Anwendung der grafischen Methode der Linearen Optimierung.
Mit Hilfe des Moduls [Algebra] - [Gleichungen] lassen sich Lösungen von Gleichungen in explizit definierter Form numerisch ermitteln und Zusammenhhänge
grafisch analysieren.
Mit Hilfe des Moduls [Algebra] - [Gleichungen] lassen sich Lösungen von Gleichungen in explizit definierter Form numerisch ermitteln und Zusammenhhänge
grafisch analysieren.
Das Teilprogramm [Algebra] - [Ungleichungen - Prinzip] ermöglicht die grafische Darstellung der Lösungsmengen linearer Ungleichungen.
Das kleine Modul [Algebra] - [Gleichungen 2.- 4. Grades] ermöglicht die Ermittlung reeller, wie komplexer Lösungen von Gleichungen 2. - 4. Grades.
Das Unterprogramm [Algebra] - [Richtungsfelder von DGL 1. Ordnung - Interaktiv] bietet die Möglichkeit, Zusammenhänge
bzgl. den Richtungsfeldern gewöhnlicher Differenzialgleichungen 1. Ordnung interaktiv grafisch zu analysieren.
Im Teilprogramm [Algebra] - [Differenzialgleichungen] - [DGL 1. Ordnung] wird es ermöglicht, Differenzial-
gleichungen 1. Ordnung numerisch iterativ lösen zu lassen.
Das Unterprogramm [Algebra] - [Differenzialgleichungen] - [DGL n-ter Ordnung] bietet die Möglichkeit, Differenzialgleichungen 2. bis 8. Ordnung numerisch
iterativ lösen zu lassen.
Die Verwendung des Moduls [Algebra] - [Differenzialgleichungen] - [DGL-Gleichungssystem] ermöglicht es, Differenzialgleichungssysteme
1. Ordnung numerisch iterativ lösen zu lassen.
Mit Hilfe des Programmmoduls [Algebra] - [Mengen] - [Mengenelemente] lassen sich Untersuchungen zum Fachthemengebiet Mengen durchführen.
Das Unterprogramm [Algebra] - [Mengen] - [Venn-Diagramm] ermöglicht die Durchführung von Mengenoperationen, sowie eine grafische Veranschaulichung
von Mengenbeziehungen anhand eines Venn-Diagramms.
Im Teilprogramm [Algebra] - Zahluntersuchung wird die Möglichkeit geboten, verschiedene Untersuchungen mit natürlichen Zahlen durchzuführen.
Das Unterprogramm [Algebra] - [Zahlen] - [Zahlen II] dient der Durchführung verschiedener numerischer Berechnungen mit speziellen Zahlen.
Mit Hilfe des kleinen Moduls [Algebra] - [Komplexe Zahlen] - [Einheitskreis komplexer Zahlen] lässt sich das Prinzip der Darstellung komplexer Zahlen in der
Gauß'schen Zahlenebene veranschaulichen.
Im Programmteil [Algebra] - [Komplexe Zahlen] - [Berechnungen mit komplexen Zahlen] können verschiedene Berechnungen mit komplexen Zahlen
durchgeführt werden.
Das Unterprogramm [Algebra] - [Komplexe Zahlen] - [Addition komplexer Zahlen] ermöglicht die Durchführung der Addition komplexer Zahlen mit Hilfe einer
Vektoraddition in der Gauß'schen Zahlenebene.
Nach Aufruf des Moduls [Algebra] - [Komplexe Zahlen] - [Multiplikation komplexer Zahlen] wird die Durchführung der Multiplikation und Division komplexer Zahlen in der
Gauß'schen Zahlenebene ermöglicht.
Das kleine Unterprogramm [Algebra] - [Sonstiges] - [Binomische Formel] ermöglicht eine grafische Interpretation der Zusammenhänge bei der binomischen
Formel 2. Grades.
Mit Hilfe des kleinen Moduls [Algebra] - [Sonstiges] - [Addition - Subtraktion] kann die Methode der Addition und Subtraktion rationaler Zahlen am Zahlenstrahl
verdeutlicht werden.
Im kleinen Unterprogramm [Algebra] - [Sonstiges] - [Irrationale Zahlen] kann die Methode der Bildung irrationaler Zahlen mit Hilfe des Satzes des Pythagoras
grafisch veranschaulicht werden.
Das kleine Zusatzmodul [Algebra] - [Sonstiges] - [Wurzellupe] bietet die Möglichkeit, sich das Prinzip der Intervallschachtelung zur Ermittlung der
Dezimaldarstellung reeller Zahlen am Beispiel des Radizierens zu veranschaulichen.
Zu diesem Fachthemengebiet sind insgesamt 43 Unterprogramme eingebunden.
Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gaußscher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL - Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
Weitere relevante Seiten zu diesem Programm
 |  |
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Weitere Videos zu einigen mit SimPlot erzeugten Animationen finden Sie unter SimPlot-Videos, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
