MathProf - Integral berechnen - Integralrechner - Integration

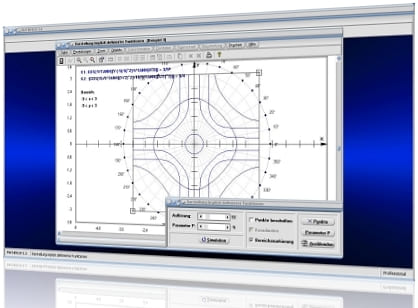
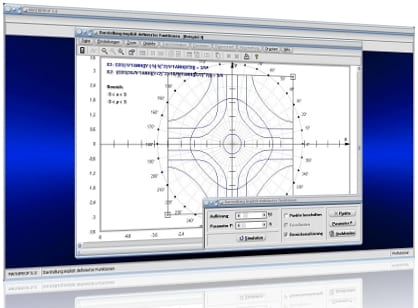
Modul Integralrechnung

---

Das Teilprogramm [Analysis] - [Integralrechnung] - Integralrechnung (Integral) bietet die Möglichkeit Integralberechnungen mit Funktionen, die in expliziter Form, in Polarform oder in Parameterform gegeben sind, durchführen zu lassen.

 

In diesem Unterprogramm steht die Durchführung der Ermittlung der folgenden bestimmten Integrale zur Verfügung:
 

• Bestimmte Integrale (Flächenberechnungen) von Funktionen in expliziter Form, beschrieben durch einen Term der Form y = f(x)

• Bestimmte Integrale (Flächenberechnungen) von Funktionen in Parameterform, beschrieben durch Terme der Form x = f(k) und y = g(k)

• Bestimmte Integrale (Flächenberechnungen) von Funktionen in Polarform, beschrieben durch einen Term der Form r = f(w) bzw. r = f(φ)
   

Die Integralrechnung (das Integrieren oder die Durchführung der Integration) ist ein Teil der Infinitesimalrechnung und bildet mit der Differentialrechnung das Themengebiet Analysis. Sie resultierte aus der Aufgabe, Flächeninhalte oder Volumina zu berechnen, die durch gekrümmte Linien bzw. Flächen begrenzt sind. Sie ist die Umkehrung des Ableitens.

Das Wort Integral ist ein Oberbegriff für das unbestimmte sowie das bestimmte Integral einer Funktion. Es sind zwei grundlegende Integrale zu unterscheiden. Hierbei handelt es sich um das unbestimmte Integral sowie das bestimmte Integral. Das unbestimmte Integral beschreibt eine Funktion und das bestimmte Integral besteht aus einem Zahlenwert. Als Integrand wird das zu Integrierende (die zu integrierende Funktion) bezeichnet, was (die) sich unterhalb des Integralzeichens befindet.
 
Nachfolgend wird auf einige grundlegende Zusammenhänge und Sachverhalte zu diesem Fachthema eingegangen.
 

Stammfunktion bilden: Als Grundintegrale oder Stammintegrale (Stammfunktionen) werden die (unbestimmten) Integrale einiger häufig verwendeter Funktionen bezeichnet. Es handelt sich um Integrale auf welche bestimmte Funktionen zurückzuführen sind.

Der Begriff Aufleiten bezeichnet die Durchführung der Integralrechnung zum Ermitteln einer Stammfunktion. Die dabei resultierende Aufleitung beschreibt die Fläche unter dem Graphen der Funktion bzw. die zwischen zwei Funktionen eingeschlossene Fläche. Ableitung rückwärts: Als Rückwärts ableiten wird das Aufleiten und somit das Ermitteln einer Stammfunktion bezeichnet.

Eine Tabelle von Stammfunktionen wird auch als Integraltafel bezeichnet. Sie umfasst die Integrale zahlreicher Funktionen, die in der Regel Funktionen mit einer Veränderlichen beinhalten. Nachfolgend aufgeführt sind einige elementare Funktionen in expliziter Form sowie deren Stammfunktionen (Stammintegrale, elementare Integrale, Integralformeln):
 
 

Funktion	Stammfunktion
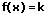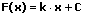		Konstante integrieren (aufleiten)
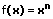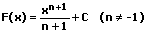		Basis integrieren (aufleiten)
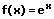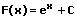		e-Funktion integrieren (aufleiten)
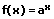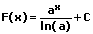		Exponent integrieren (aufleiten)
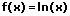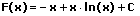		Logarithmus integrieren (aufleiten)
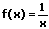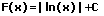		Reziproke integrieren (aufleiten)
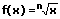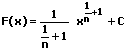		Wurzel integrieren (aufleiten)
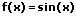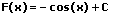		Sinus integrieren (aufleiten)
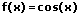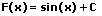		Cosinus integrieren (aufleiten)
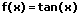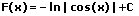		Tangens integrieren (aufleiten)
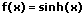		Sinus hyperbolicus integrieren (aufleiten)
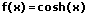		Cosinus hyperbolicus integrieren (aufleiten)

 
 

 

Im Weiteren erfolgt die Ausgabe der Integrationsregeln, welche bei der Durchführung der symbolischen Integration (beim Aufleiten bzw. Integrieren) gelten. Bei den Integrationsregeln handelt es sich um Regeln, die bei der Durchführung der Integration zu beachten sind.
 
 
1. Potenzregel:
 

 
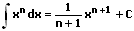
Die Potenzregel findet dann Anwendung, wenn ein zu berechnendes Integral eine Potenzfunktion der Form xⁿ beinhaltet. In diesem Fall wird der Exponent um die Zahl 1 erhöht und die entsprechende Variable (x) wird durch diese neue Hochzahl geteilt.

Beispiele zur Potenzregel:
 


 
 
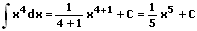
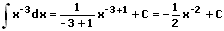
2. Faktorregel:
 

 
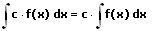
Die Faktorregel der Integralrechnung besagt, dass ein konstanter Faktor vor das Integral gezogen werden darf.

Beispiele zu Faktorregel:
 


 
 
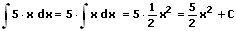
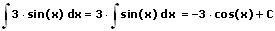
3. Summenregel:
 

 
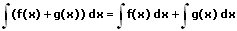
Die Summenregel besagt, dass Funktionen die durch eine Summe im Integral voneinander getrennt sind, jeweils einzeln (separat voneinander) integriert und hierauf addiert werden können.

Beispiele zur Summenregel:
 


 
 
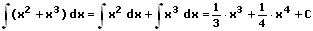
4. Differenzenregel:
 


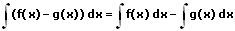
Die Differenzenregel besagt, dass Funktionen die durch eine Differenz im Integral voneinander getrennt sind, jeweils einzeln (separat voneinander) integriert und hierauf subtrahiert werden können.

 
Beispiele:
 


 
 
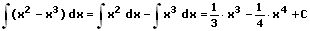
5. Partielle Integration:
 
Bei einem Integral der Form



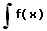
wird die Funktion f(x) in ein Produkt aus der Funktion u(x) und der Ableitung v'(x) einer Funktion v(x) zerlegt:



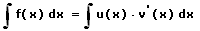
Dieses Integral lässt sich hierauf wie folgt darstellen:


 


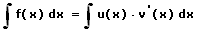
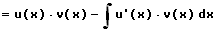
Die partielle Integration kann sowohl für unbestimmte wie auch für bestimmte Integrale Anwendung finden. In bestimmten Fällen ist diese Vorgehensweise mehrmals aufeinanderfolgend zu praktizieren bis auf ein Grundintegral gestossen wird. Eine derartige Integration wird auch mit dem Begriff Produktintegration bezeichnet.

Beispiel:

Es gilt die Funktion ∫x·cos(x) dx partiell zu integrieren.

1. Es erfolgt die Zerlegung des Integranden in nachfolgend gezeigte Faktorfunktionen:

u(x) = x
v'(x) = cos(x)

u'(x) = 1
v(x) = sin(x)

2. Hierauf erfolgt die Durchführung der partiellen Integration:

∫ x·cos(x) dx = x·sin(x) - ∫1·sin(x) dx = x·sin(x) + cos(x) + C
 
 
6. Logarithmische Integration - Logarithmische Substitution:

Ist eine Funktion der nachfolgend gezeigten Art gegeben



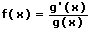
so existiert eine Stammfunktion der Form:


  
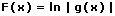
Logarithmisches Integrieren (die logarithmische Integration) findet dann Anwendung, wenn sich die Ableitung einer zu integrierenden Funktion im Zähler eines Bruchs befindet und diese Funktion in dessen Nenner vorkommt.

Beispiel:

Gegeben sei die Funktion: f(x)=2x/(x²+1)

Es gilt die Stammfunktion dieser Funktion zu ermitteln. Es kann festgestellt werden, dass sich die 1. Ableitung der im Nenner stehenden Funktion im Zähler dieses Bruchs befindet. Somit kann die logarithmische Integration angewandt werden und es resultiert:

F(x)= ln(x²+1)+C
   

Lineare Substitution

 
Lineare Substitution:

Beim Integrieren verketteter Funktionen kommt die Integration durch Substitution zum Einsatz. Bei der Durchführung der linearen Substitution handelt es sich um einen Spezialfall dieser Art der Praktizierung der Integration.
 
Wenn die innere Funktion eine lineare Funktion ist, so kann das Integrieren verketteter Funktionen der Form u(v(x)) mittels nachfolgend gezeigter Regel durchgeführt werden:

∫f(mx+n)dx = 1/mF(mx+n)+C

Diese Vorgehensweise wird als lineare Substitution bezeichnet und darf lediglich dann angewandt werden, wenn es sich bei der inneren Funktion v(x) um eine lineare Funktion der Form v(x) = mx+n handelt. Liegt dieser Sachverhalt vor, so kann die Stammfunktion mittels der Anwendung einer linearen Substitution ermittelt werden.
 
Hierzu kann nachfolgend gezeigtes Vorgehen praktiziert werden.

1. Der gegebene Term ist in Form eines Produkts zu schreiben (konstante Faktoren bleiben hierbei erhalten)
2. Die zusammengesetzte Funktionen wird in die innere Funktion v(x) und die äußere Funktion u(v) zerlegt
3. Es wird die Stammfunktion der äußeren Funktion gebildet und in die innere Funktion eingesetzt
4. Hierauf wird dieser Ausdruck mit dem Kehrwert der inneren Ableitung multipliziert und der konstante Faktor wird davor positioniert
5. Sind keine Integrationsgrenzen bekannt, so wird dem resultierenden Term die Konstante C hinzuaddiert
6. Zum Schluss erfolgt durch das Ableiten des ermittelten Ergebnisses eine Überprüfung dessen

Beispiel:

Gegeben sei die Funktion f(x) = 5/(6x - 1)³

zu 1. Mittels der Formulierung der Funktion in Form eines Produkts resultiert der Term f(x) = 5⋅(6x - 1)⁻³
zu 2. Als konstanter Faktor wird die Zahl 5 festgelegt
zu 3. Beim Term (6x - 1)⁻³ handelt es sich um eine zusammengesetzte Funktion der Form u(v(x)). Diese setzt sich aus der äußeren Funktion u(v) = v⁻³ und der inneren Funktion v(x) = 6x - 1 zusammen
zu 4. Bei der Bildung der Stammfunktion der äußeren Funktion ergibt sich der Term U(v) = -1/2⋅v⁻². Ein Einsetzen der inneren Funktion v(x) = 6x - 1 in die äußere Funktion ergibt den Term -1/2⋅(6x - 1)⁻²
zu 5. Die innere Ableitung v'(x) ergibt sich mit v'(x) = 6. Ihr Kehrwert lautet 1/4. Somit ergibt sich als Ergebnis:

F(x) = −5⋅1/6⋅1/2⋅(6 x−1)⁻² + C bzw. F(x) = -5/12⋅(6 x−1)⁻² + C
  

 Integrationsgrenzen - Vertauschung

 
Integrationsgrenzen werden verwendet, um mit Hilfe der Integralrechnung exakte Flächenstücke zu berechnen, welche durch eine Funktion und die Abszisse oder durch zwei Funktionen begrenzt werden. Es wird zwischen der oberen und der unteren Integrationsgrenze unterschieden. Die untere dieser wird unterhalb des Integralsymbols definiert, die obere wird oberhalb dessen geschrieben. Integrationsgrenzen können vertauscht werden. Normalerweise wird der kleinere dieser Werte als untere Grenze definiert und der größere als Obergrenze. Es besteht jedoch die Möglichkeit, diese Grenzen zu vertauschen. Hierbei gilt folgender Sachverhalt:
 

 
 

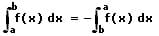
Bestimmtes Integral - Unbestimmtes Integral - Definition - Hauptsatz der Differential- und Integralrechnung - Schreibweise

 
Grundsätzlich kann gesagt werden, dass der zwischen einem bestimmten und einem unbestimmten Integral bestehende Unterschied darin liegt, dass bestimmte Integrale über Integrationsgrenzen verfügen, welche unbestimmte Integrale nicht besitzen.
 
Bestimmtes Integral:

Ist f(x) eine im Intervall I = [a,b] stetige Funktion mit im Intervall nicht negativen Funktionswerten, so ist das bestimmte Integral der Flächeninhalt zwischen dem Graphen der Funktion, der Abszisse und den vertikalen Geraden x₁ = a und x₂ = b. Dieser Wert wird auch als Integralwert bezeichnet. Für die Durchführung einer Berechnung dieser Art wird der Ausdruck Integral bestimmen verwendet.
 



 
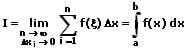
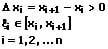
Unbestimmtes Integral:

Ein unbestimmtes Integral ist die Menge aller Stammfunktionen. Es besitzt keine Integralgrenzen. Jede Funktion f(x) besitzt unendlich viele Stammfunktionen und besitzt die Form F(x) + C. Die Konstante C wird als Integrationskonstante oder additive Konstante bezeichnet. Sie bewirkt eine Parallelverschiebung des Graphen der Stammfunktionen in vertikaler Richtung. Das unbestimmte Integral stellt geometrisch eine Schar unendlich vieler kongruenter Kurven dar, welche durch vertikale Parallelverschiebung entlang der y-Achse auseinander hervorgehen.





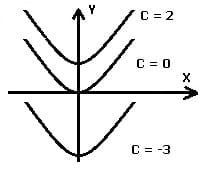
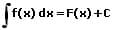
Hauptsatz der Differential- und Integralrechnung:

Der Hauptsatz der Differential- und Integralrechnung stellt die Beziehung zwischen Stammfunktionen und Integralen her. Dieser besagt, dass wenn f eine stetige Funktion auf dem Intervall I = [a,b] ist, folgendes gilt:


 
 

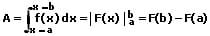
Mittelwertsatz - Linearer Mittelwert

 
Linearer Mittelwert:



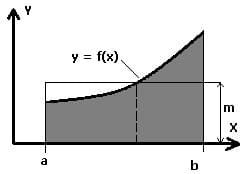
Der lineare Mittelwert m einer stetigen Funktion f(x) im Intervall [a;b] ist:



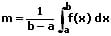
m: Durchschnittlicher Funktionswert von f in [a,b]

Der Mittelwertsatz der Integralrechnung garantiert im Intervall [a,b] mindestens einen Wert, für den gilt:



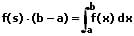
f(s): Durchschnittlicher Funktionswert von f in [a,b]
 
 

Integrierbarkeit - Uneigentliche Integrale - Unendliches Intervall

 
Integrierbarkeit:

Eine Funktion ist in <a,b> integrierbar, wenn sie

- beschränkt in <a,b> nur endlich viele Unstetigkeitsstellen besitzt
- im Bereich <a,b> stetig ist
- monoton ist

Uneigentliche Integrale:

Uneigentliches Integral: Integrale mit unendlichen Grenzen (Polen) und Integrale die im Integrationsintervall unendlich werden, werden als uneigentliche Integrale bezeichnet. Ihre Definitionsformen sind nachfolgend aufgeführt.

  

   
 

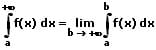
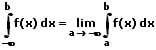
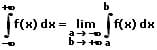
Flächeninhalte
(Funktionen mit einer Variable)

  
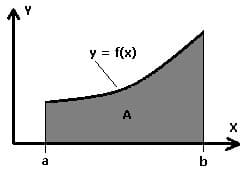
1. Flächeninhalt zwischen einer Kurve in kartesischen Koordinaten und der x-Achse:

Der Flächeninhalt A, welcher von einer explizit definierten Kurve y = f(x) sowie der x-Achse innerhalb des Intervalls [a,b] beschrieben wird, kann mit der unten stehenden Formel ermittelt werden. Die hierbei als "Flächeninhaltsfunktion" bezeichnete Funktion F(x) beschreibt den (orientierten) Flächeninhalt (die orientierte Fläche), der zwischen dem Graphen der Funktion f(x) und der x-Achse innerhalb des Intervalls [a,b] besteht.





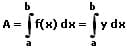
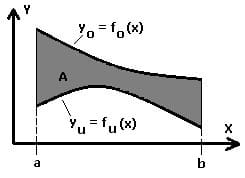
2. Flächeninhalt zwischen zwei Kurven in kartesischen Koordinaten:

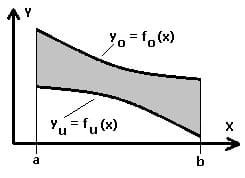
Der Flächeninhalt A, der von den zwei explizit definierten Kurven y₀ = f(x) und y_u = f(x) innerhalb des Intervalls [a,b] beschrieben wird, berechnet sich wie nachfolgend aufgeführt.




 
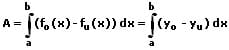
Unter einer Flächenbilanz wird die gegenseitige Verrechnung der sich oberhalb und unterhalb der Abszisse befindenen Teilflächen verstanden. Eine Funktion die Integrationsgrenzen bildet wird als Randfunktion bezeichnet.
 
3. Flächeninhalt zwischen einer Kurve in Parameterform und der x-Achse:

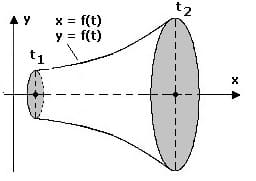
Der Flächeninhalt A, der von einer Kurve, welche durch die Parametergleichungen x = f(t) und y = f(t) innerhalb des Intervalls [t₁,t₂] beschrieben wird sowie der x-Achse gebildet wird, lässt sich wie folgt berechnen.





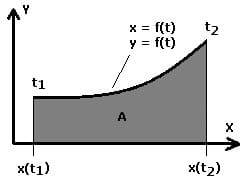
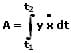
Mit:


 
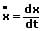
4. Flächeninhalt zwischen einer Kurve in Parameterform und dem Koordinatenursprung (Leibnizsche Sektorenformel):

Der Flächeninhalt A, welcher von einer Kurve, die durch die Parametergleichungen x = f(t) und y = f(t) innerhalb des Intervalls [t₁,t₂] beschrieben wird und durch zwei auf der x-Achse liegende Punkte x_(t1) und x_(t2) gebildet wird, lässt sich ermitteln mit:






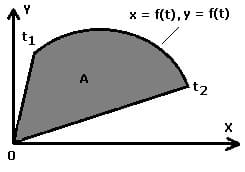
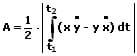
Mit:




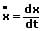
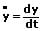
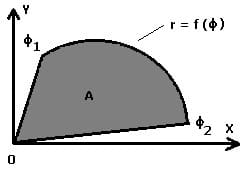
5. Flächeninhalt zwischen einer Kurve in Polarform und dem Koordinatenursprung:

Der Flächeninhalt A, der von einer Kurve, die durch die Polarkoordinaten r = f(φ) innerhalb des Intervalls [φ₁,φ₂] beschrieben wird und dem Koordinatenursprung gebildet wird, berechnet sich wie folgt.


 

 
 

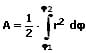
Schwerpunkte ebener Flächen - Flächenschwerpunkt

 
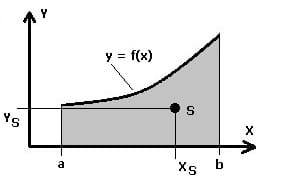
Schwerpunkt einer homogenen ebenen Fläche (Flächenschwerpunkt) I:

Die Schwerpunktkoordinaten (der Flächenschwerpunkt) S(x_s;y_s) einer homogenen ebenen Fläche A, welche von einer explizit definierten Kurve y = f(x) sowie der x-Achse innerhalb des Intervalls [a,b] beschrieben wird, sind nachfolgend aufgeführt.

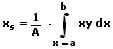
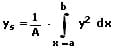
Schwerpunkt einer homogenen ebenen Fläche (Flächenschwerpunkt) II:

Die Schwerpunktkoordinaten (der Flächenschwerpunkt) S(x_s;y_s) einer homogenen ebenen Fläche A, welche von den Kurven y₀ = f_o(x) und y_u = f_u(x) zwischen den Grenzen x = a und x = b eingeschlossen wird, sind nachfolgend aufgeführt (y₀ > yu).

 
 

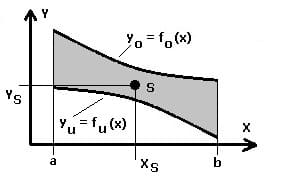
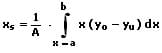
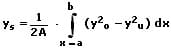
Bogenlänge - Kurvenlänge

 
Die Bogenlänge (Kurvenlänge) einer ebenen Kurve beschreibt die Länge der Kurve, die diese zwischen zwei Punkten A und B besitzt.

1. Bogenlänge eines Kurvenstücks, beschrieben durch eine Funktion in kartesischer Form:

Die Bogenlänge s eines ebenen Kurvenstücks, welches von einer explizit definierten Kurve y = f(x) über das Intervall [a,b] beschrieben wird, lässt sich wie nachfolgend gezeigt berechnen.

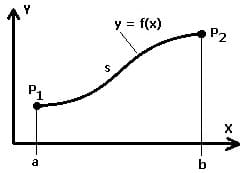
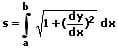
2. Bogenlänge eines Kurvenstücks, beschrieben durch Funktionen in Parameterform:

Die Bogenlänge s eines ebenen Kurvenstücks, welches durch die Parametergleichungen x = f(t) und y = f(t) innerhalb des Intervalls [t₁,t₂] beschrieben wird, lässt sich mit nachfolgend gezeigter Formel berechnen.





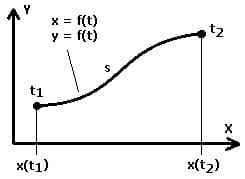
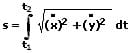
Mit:

 

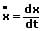
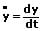
3. Bogenlänge eines Kurvenstücks, beschrieben durch eine Funktion in Polarform:

Die Bogenlänge s eines ebenen Kurvenstücks, welches durch die Polarkoordinaten r = f(φ) innerhalb des Intervalls [φ₁,φ₂] beschrieben wird, berechnet sich wie folgt.





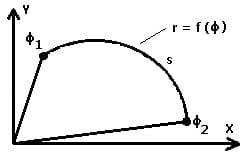
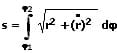
Mit:


 
 

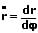
Linienschwerpunkt

 
Linienschwerpunkt einer Kurve, beschrieben durch eine Funktion in kartesischer Form:

Der Schwerpunkt S(x_s;y_s) einer Linie l, welche durch eine Funktion in kartesischer Form beschrieben wird, kann wie folgt berechnet werden:




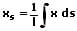
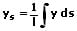
Bei zusammengesetzten Linien berechnet sich der Linienschwerpunkt S(x_s;y_s) aus der Summe i einzelner Linienschwerpunkte. Es gilt:





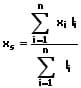
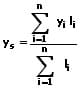
Ein Linienschwerpunkt befindet bei aus zusammengesetzten Linien meist außerhalb des Linienverlaufs.
 
 

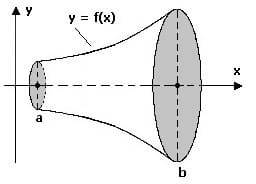
Volumen von Rotationskörpern

Durch Drehung einer ebenen Kurve um die in der Kurvenebene liegende Rotationsachse entsteht ein Rotationskörper, dessen Volumen als Rotationsvolumen bezeichnet wird.

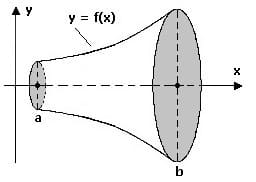
Das Volumen V_x des Rotationskörpers, welches durch die Drehung einer Kurve y = f(x) innerhalb des Intervalls [a,b] um die x-Achse beschrieben wird, kann wie nachfolgend gezeigt errechnet werden:




 
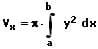
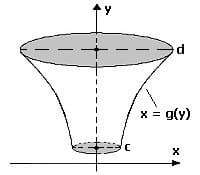
Das Volumen V_y des Rotationskörpers, welches durch die Drehung einer Kurve x = g(x) innerhalb des Intervalls [c,d] um die y-Achse beschrieben wird, kann wie nachfolgend gezeigt errechnet werden:




 
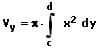
Das Volumen V_x des Rotationskörpers, welches durch die Drehung einer Kurve die durch die Parametergleichungen x = f(t) und y = f(t) innerhalb des Intervalls [t₁,t₂] um die x-Achse beschrieben wird, kann wie nachfolgend gezeigt errechnet werden:





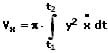
Mit:


   
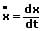
Das Volumen V_y des Rotationskörpers, welches durch die Drehung einer Kurve die durch die Parametergleichungen x = f(t) und y = f(t) innerhalb des Intervalls [t₁,t₂] um die y-Achse beschrieben wird, kann wie nachfolgend gezeigt errechnet werden:




 

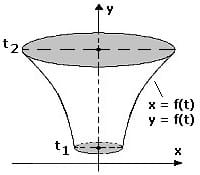
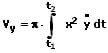
Mit:


 

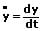
Mantelfläche von Rotationskörpern

Durch Drehung einer ebenen Kurve um die in der Kurvenebene liegende Rotationsachse entsteht eine Fläche, welche als Mantelfläche bezeichnet wird.

Die Mantelfläche M_x des Rotationskörpers, welche durch die Drehung einer Kurve y = f(x) innerhalb des Intervalls [a,b] um die x-Achse beschrieben wird, kann wie nachfolgend gezeigt errechnet werden:




 
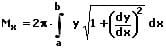
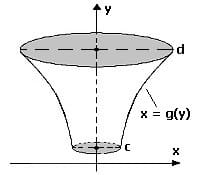
Die Mantelfläche M_y des Rotationskörpers, welche durch die Drehung einer Kurve x = g(y) innerhalb des Intervalls [c,d] um die y-Achse beschrieben wird, kann wie nachfolgend gezeigt errechnet werden:




 

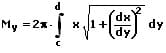
Schwerpunkte von Rotationskörpern

Jeder Körper kann als ein System von Massenpunkten aufgefasst werden. Es existiert stets ein Punkt, in welchem die Gesamtmasse des Körpers als vereinigt gedacht werden kann. Dieser Punkt wird als Massenmittelpunkt bzw. Schwerpunkt bezeichnet.

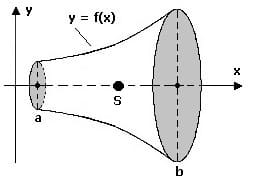
Rotiert die Kurve einer Funktion y = f(x) um die x-Achse, so liegt der Schwerpunkt S(x_s,y_s) dieser Rotationsfläche auf dieser Achse.




 
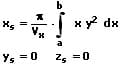
Rotiert die Kurve einer Funktion x = g(y) um die y-Achse, so liegt der Schwerpunkt S(x_s,y_s) dieser Rotationsfläche auf dieser Achse.

 

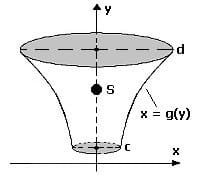
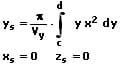
Flächenmoment 1. Grades - Statisches Moment - Statisches Flächenmoment

Die Gewichtskraft G eines Punktes M mit der Masse m erzeugt im Abstand r von der vertikalen Achse von einer Drehachse ein statisches Moment vom Betrag M = mgr. Dieses beschreibt die Größe des Widerstands einer Querschnittsfläche gegen ihre Verformung. Ein statisches Moment wird auch als Flächenmoment 1. Grades bezeichnet. Es dient unter anderem der Berechnung des Schwerpunktes einer Fläche.



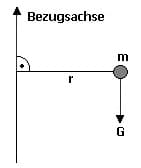
Das statische Moment einer Kraft bezüglich der x-Achse berechnet sich wie folgt:



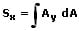
Das statische Moment einer Kraft bezüglich der y-Achse berechnet sich wie folgt:


 
 

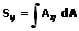
Flächenträgheitsmoment - Flächenmoment 2. Grades

Bei einem Flächenmoment (2. Grades) oder Flächenträgheitsmoment handelt es sich um eine Größe, die im Zusammenhang mit Biegemomenten bei Balken und Trägern auftritt. Sie sind auf bestimmte Achsen bezogene Größen der Dimension Länge. Es wird zwischen axialen Flächenmomenten und polaren Flächenmomenten unterschieden.

Axiales Flächenmoment (axiales Flächenträgheitsmoment): Bei axialen Momenten dieser Art befindet sich die Bezugsachse in der Flächenebene.
Polares Flächenmoment (polares Flächenträgheitsmoment): Bei polaren Flächenmomenten ist diese Bezugsachse vertikal zur Flächenebene ausgerichtet.

Nachfolgend aufgeführt sind die Formeln zur Berechnung der axialen Flächenmomente bzgl. der x- Achse und y-Achse sowie des polaren Flächenmoments zweiten Grades bzgl. des Nullpunkts.
 








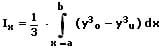
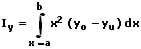
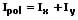
I_x: Axiales Flächenmoment bezüglich der x-Achse
I_y: Axiales Flächenmoment bezüglich der y-Achse
I_pol: Polares Flächenmoment bezüglich des Nullpunkts  

  
 

Doppelintegral - Flächenträgheitsmoment - Flächenmoment - Trägheitsmoment - Schwerpunkt - Mehrdimensionale Integration - Zweidimensionales Integral (Funktionen mit zwei verschiedenen Variablen)

 
Bei einem multiplen Integral handelt es sich um ein bestimmtes Integral einer Funktion mehrerer reeller Variablen. Integrale dieser Art tragen die Bezeichnung Mehrfachintegrale. Die einfachste Art derartiger Integrale sind Doppelintegrale. Die Berechnung solcher Integrale wird als mehrdimensionale Integration bezeichnet.

Doppelintegral: Anwendung findet die Bildung von Doppelintegralen unter anderem bei der Berechnung von Flächeninhalten (welche durch zwei Funktionen mit unterschiedlichen Variablen gebildet bzw. beschrieben werden), der Berechnung des Schwerpunkts einer Fläche sowie der Berechnung von Flächenträgheitsmomenten (Flächenmomenten). Die Berechnung eines Doppelintegrals erfolgt von innen nach außen. Dies wird durch zwei aufeinanderfolgende gewöhnliche Integrationen (Schritte) durchgeführt.


 
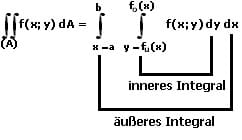
I - Verwendung kartesischer Koordinaten:

Doppelintegral unter Verwendung kartesischer Koordinaten:



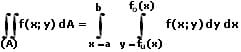
Innere Integration:

Bei Durchführung der inneren Integration wird die Variable x zunächst als Konstante betrachtet und die Funktion f(x,y) wird unter Anwendung der für gewöhnliche Integrale geltenden Regeln nach der inneren Variable y integriert. In die hierbei ermittelte Stammfunktion werden hierauf für y die Integrationsgrenzen f_o(x) sowie f_u(x) eingesetzt und es wird die entsprechende Differenz gebildet.

Äußere Integration:

Die mittels der Anwendung der inneren Integration erhaltene Funktion, welche lediglich noch von der Variable x abhängt, werden hierauf die Grenzen von x = a sowie x = b eingesetzt. Mit dieser Funktion wird dann eine gewöhnliche Integration nach x durchgeführt.
 
II - Verwendung von Polarkoordinaten:

Doppelintegral unter Verwendung von Polarkoordinaten:



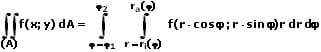
Die Durchführung der Doppelintegration unter Verwendung von Polarkoordinaten erfolgt prinzipiell gleich wie nach der oben beschriebenen Methode. Zur Umwandling kartesischer Koordinaten in Polarkoordinaten gelten die nachfolgend gezeigten Transformationsgleichungen:

x = r·cos φ
y = r·sin φ

Die Grenzen des entsprechenden Integrals werden in Polarkoordinaten ausgedrückt. Die Variablentransformation erfolgt, indem x = r·cos φ sowie y = r·sin φ und dA = r dr dφ gesetzt werden.

Innere Integration:

Bei Praktizierung der inneren Integration unter Verwendung von Polarkoordinaten wird die Variable r zunächst als Konstante betrachtet und die Funktion f(r,φ) wird unter Anwendung der für gewöhnliche Integrale geltenden Regeln nach der inneren Variable φ integriert. In die hierbei ermittelte Stammfunktion werden hierauf für φ die Integrationsgrenzen ra(φ) sowie ri(φ) eingesetzt und es wird die entsprechende Differenz gebildet.

Äußere Integration:

Die mittels der Ausführung der inneren Integration erhaltene Funktion, welche lediglich noch von der Variable φ abhängt, werden hierauf die Grenzen von φ = φ₁ sowie φ = φ₂ eingesetzt. Mit dieser Funktion wird dann eine gewöhnliche Integration nach φ durchgeführt.
 
III - Flächeninhalt zwischen zwei Funktionen:

Der Flächeninhalt, welcher durch zwei Funktionen gebildet (beschrieben) wird, kann mittels der nachfolgend gezeigten Formeln (Doppelintegrale) berechnet werden.

In kartesischen Koordinaten:



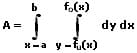
In Polarkoordinaten:



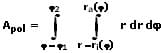
A: Flächeninhalt des Bereichs bei Verwendung kartesischer Koordinaten
A_Pol: Flächeninhalt des Bereichs bei Verwendung polarer Koordinaten
 
IV - Schwerpunkt einer Fläche:

Der Schwerpunkt S(x_s,y_s) einer homogenen ebenen Fläche, welche durch zwei Funktionen beschrieben wird, kann folgendermaßen berechnet werden.

In kartesischen Koordinaten:





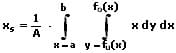
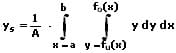
In Polarkoordinaten:




 
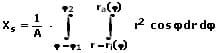
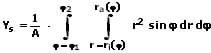
x_s,y_s: Koordinaten des Flächenschwerpunkts
f_o: Obere Kurve
f_u: Untere Kurve

V - Flächenträgheitsmoment - Flächenmoment:

Die Bestimmung von Flächenmomenten 2. Grades (Flächenträgheitsmomenten) unter der Bildung von Doppelintegralen erfolgt durch die Verwendung nachfolgend aufgeführter Formeln.
 
Axiales Flächenmoment 2. Grades (Flächenträgheitsmoment) in kartesischen Koordinaten:







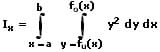
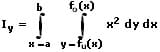
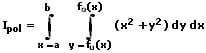
I_x: Axiales Flächenmoment der Fläche A bezüglich der x-Achse
I_y: Axiales Flächenmoment der Fläche A bezüglich der y-Achse
I_pol: Polares Flächenmoment der Fläche A bezogen auf eine orthogonale Bezugsachse (z-Achse), welche senkrecht zur Flächenebene durch den Koordinatenursprung verläuft
f_o: Obere Kurve
f_u: Untere Kurve

Axiales Flächenmoment 2. Grades (Flächenträgheitsmoment) in Polarkoordinaten:






 
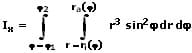
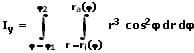
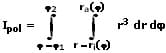
I_x: Axiales Flächenmoment der Fläche A bezüglich der x-Achse
I_y: Axiales Flächenmoment der Fläche A bezüglich der y-Achse
I_pol: Polares Flächenmoment der Fläche A bezogen auf eine orthogonale Bezugsachse (z-Achse), welche senkrecht zur Flächenebene durch den Koordinatenursprung verläuft
r_o: Obere Kurve
r_u: Untere Kurve

---

 

Definitionen einiger Fachbegriffe

 
Definitionen:
 

Das Flächenintegral (Oberflächenintegral) ist eine Verallgemeinerung des eindimensionalen Integralbegriffes mit Absicht der
Anwendung auf ebenen oder gekrümmten Flächen. Es beschreibt eine Integration über eine (gerichtete) Fläche.

Ein Volumenintegral (Dreifachintegral) ist ein Spezialfall der mehrdimensionalen Integralrechnung, der vor allem in der Physik Anwendung findet.



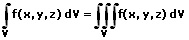
Die Berechnung eines derartigen Integrals erfolgt durch eine dreimalig aufeinanderfolgende gwewöhnliche Integration. Die Durchführung einer Intgralrechnung dieser Art erfolgt jeweils über die Koordinaten eines dreidimensionalen Raums.


Parameterintegral: Mit dem Begriff Parameterintegral wird in der Analysis die Art eines Integrals bezeichnet, dessen Integrand von einem Parameter abhängig ist. Ein sehr bekanntes Beispiel hierfür ist die Gammafunktion:


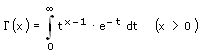
In diesem Fall ist x der Parameter, von dem der Integrand und somit auch das Integral abhängt.
  

Massenträgheitsmoment - Satz von Steiner

Massenträgheitsmomente:

Das Massenträgheitsmoment ist ein Maß für die Trägheit eines starren Körpers bei der Rotation um eine Achse und entspricht der Masse bei der Translation. Es beschreibt dessen Trägheit gegenüber einer Änderung seiner Winkelgeschwindigkeit auf einer Kreisbahn bzw. den Widerstand eines starren Körpers gegenüber der Veränderung seiner ausgeführten Drehbewegung. Die Berechnung eines Massenträgheitsmoments ist ausschließlich dann möglich, wenn die Masse sowie deren Verteilung bekannt sind. Diese kann punktförmig, flächenhaft oder räumlich gegeben sein.

Die allgemeine Definition des Massenträgheitsmoments eines räumlichen Körpers mit homogener Massenverteilung lautet:





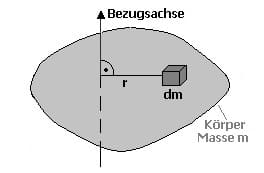
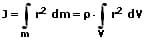
d_m: Massenelement
d_V: Volumenelement
r: Vertikale Distanz des Massenelements (Volumenelements) von Bezugsachse
ρ: Dichte des Körpers

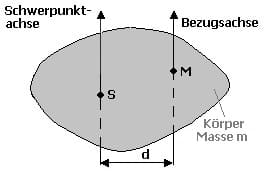
Satz von Steiner:

Massenträgheitsmomente die auf eine durch den Körperschwerpunkt S verlaufende Drehachse bezogen werden, werden mit dem Satz von Steiner beschrieben und tragen die Bezeichnung J_s. Ist das Trägheitsmoment J_s eines Körpers bekannt, so kann mit Hilfe dieses Satzes dessen Trägheitsmoment bezogen auf eine zur Schwerpunktachse parallel verlaufende Bezugsachse A berechnet werden. Die Definition des Satz von Steiner lautet:





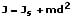
J: Massenträgheitsmoment hinsichtlich der Bezugsachse
J_s: Massenträgheitsmoment hinsichtlich der Schwerpunktachse (parallel zur Bezugsachse)
m: Masse des Körpers
d: Abstand der Bezugsachse und der Schwerpunktachse


Massenträgheitsmomente homogener Rotationskörper:

Massenträgheitsmomente homogener Rotationskörper J_x, welche durch die Rotation der Kurve einer Funktion y = f(x) um die x-Achse entstehen, können wie nachfolgend gezeigt berechnet werden:





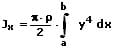
ρ: Dichte des Rotationskörpers

Massenträgheitsmomente homogener Rotationskörper J_y, welche durch die Rotation der Kurve einer Funktion x = g(y) um die y-Achse entstehen, können wie nachfolgend gezeigt berechnet werden:





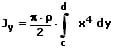
ρ: Dichte des Rotationskörpers

 

Bei der Wahl des Registerblatts Funktionen in expliziter Form können u.a. sowohl der Flächeninhalt zwischen einer Funktion der Form f(x) und der Abszisse, wie auch der Flächeninhalt, welcher von zwei Funktionen f1(x) und f2(x) eingeschlossen wird, innerhalb eines festgelegten Intervallbereichs (Integrationsgrenzen) errechnet werden.
 

Wird in nur einem Eingabefeld ein Term deklariert, bleibt das zweite leer und wird das entsprechende Kontrollkästchen aktiviert, so ermittelt das Programm für diese Funktion per Voreinstellung:
 

• Fläche (Flächeninhalt) orientiert A(o)
  Fläche (Flächeninhalt) zwischen der Funktion und der x-Achse (bestimmtes Integral)

• Fläche (Flächeninhalt) absolut A(a)
  Betrag der Fläche, unabhängig davon ob Flächensegmente sich oberhalb oder unterhalb der Abszissenachse befinden
   
• Bogenlänge s der Kurve
• Schwerpunkt der Kurve
• Schwerpunkt des Flächensegments (Flächenschwerpunkt)

• Volumen/Rotationsvolumen (abs.) V(x) des bei Rotation der Kurve um die x-Achse entstehenden Körpers
• Volumen/Rotationsvolumen (abs.) V(y) des bei Rotation der Kurve um die y-Achse entstehenden Körpers, wenn Fläche unter der Kurve bzgl. der x-Achse verwendet wird
• Volumen/Rotationsvolumen (abs.) V(y) des bei Rotation der Kurve um die y-Achse des entstehenden Körpers, wenn Fläche (Flächeninhalt) unter der Kurve bzgl. der y-Achse verwendet wird
   
• Mantelfläche/Rotationsfläche (abs.) A(x) des bei Rotation der Kurve um die x-Achse entstehenden Körpers
• Mantelfläche/Rotationsfläche (abs.) A(y) des bei Rotation der Kurve um die y-Achse entstehenden Körpers
   
• Statisches Moment Mx des Kurvenstücks
• Statisches Moment My des Kurvenstücks
• Statisches Moment Mx des Flächenstücks
• Statisches Moment My des Flächenstücks

 
Werden in beiden Eingabefeldern f1(x) = und f2(x) = Funktionen definiert und die entsprechenden Kontrollkästchen aktiviert, so ermittelt der Integralrechner des Programms für diese per Voreinstellung:
 

• Fläche (Flächeninhalt) orientiert A(o)
  Fläche (Flächeninhalt) zwischen beiden Funktion (bestimmtes Integral)

• Fläche (Flächeninhalt) absolut A(a)
  Betrag der Summe aller zwischen beiden Funktionen eingeschlossenen Flächensegmente

 
Für die im oberen Eingabefeld definierte Funktion f1(x) = wird zusätzlich ausgegeben:
 

• Bogenlänge s der Kurve
• Schwerpunkt der Kurve
• Schwerpunkt des Flächensegments (Flächenschwerpunkt)

• Volumen/Rotationsvolumen (abs.) V(x) des bei Rotation der Kurve um die X-Achse entstehenden Körpers
• Volumen/Rotationsvolumen (abs.) V(y) des bei Rotation der Kurve um die Y-Achse entstehenden Körpers, wenn Fläche unter der Kurve bzgl. der x-Achse verwendet wird
• Volumen (abs.) V(y) des bei Rotation der Kurve um die Y-Achse des entstehenden Körpers, wenn Fläche (Flächeninhalt) unter der Kurve bzgl. der y-Achse verwendet wird
   
• Mantelfläche/Rotationsfläche (abs.) A(x) des bei Rotation der Kurve um die X-Achse entstehenden Körpers
• Mantelfläche/Rotationsfläche (abs.) A(y) des bei Rotation der Kurve um die Y-Achse entstehenden Körpers
   
• Statisches Moment Mx des Kurvenstücks
• Statisches Moment My des Kurvenstücks
• Statisches Moment Mx des Flächenstücks
• Statisches Moment My des Flächenstücks

 

Hinweise:

Der Schwerpunkt des Flächensegments wird nur ausgegeben, wenn die Werte definierter Funktionen innerhalb des gewählten Untersuchungsbereichs keinen Vorzeichenwechsel aufweisen. Das Rotationsvolumen, welches eine Funktion bei Rotation um die y-Achse bildet, kann auf zwei verschiedene Weisen errechnet werden. In diesem Unterprogramm wird dieses nicht über die Umkehrfunktion errechnet, sondern über den angegebenen Wertebereich bzgl. der x-Achse (näheres siehe Fachliteratur).

 

Um Untersuchungen zu diesem Fachthema mit parameterhaltigen Funktionen durchzuführen, verwenden Sie das Unterprogramm Integralrechnung - Interaktiv.

 
 

 
Sollen Integralberechnungen mit Funktionen in expliziter Form durchgeführt und hierfür relevante Zusammenhänge grafisch dargestellt werden, so gehen Sie wie nachfolgend geschildert vor:
 

1. Definieren Sie eine Funktion im Eingabefeld mit der Bezeichnung f1(x) =. Sollen Berechnungen mit zwei Funktionen durchgeführt werden, so ist eine weitere Funktion im darunter angeordneten Eingabefeld mit der Bezeichnung f2(x) = zu definieren. Beachten Sie hierbei die geltenden Syntaxregeln.
   
   Aktivieren Sie das/die entsprechende(n) Kontrollkästchen mit den Bezeichnungen f1(x)= bzw. f2(x)=.
    
2. Legen Sie durch die Eingabe entsprechender Zahlenwerte den Wertebereich fest, über welchen die numerische Integration durchgeführt werden soll (Integration von x1 = und bis x2 =).
    
3. Bestimmen Sie mittels dem zur Verfügung stehenden Rollbalken Stützstellen die Anzahl der für die Berechnungen zu verwendenden Stützstellen.
    
4. Nach einem Klick auf die Schaltfläche Berechnen werden die ermittelten Ergebnisse in der Listbox ausgegeben.
    
5. Bedienen Sie hierauf die Schaltfläche Darstellen. Die Flächenmarkierung bei Ausgabe der Darstellung erfolgt über den Abszissen-Bereich, der im Formularbereich Integration von x1 = und bis x2 = festgelegt wurde.
    
6. Soll der Bereich über welchen die Integration durchgeführt werden soll exakt festgelegt werden, so führen Sie einen Klick auf die Schaltfläche Punkte auf dem Bedienformular aus und geben die relevanten Grenzwerte im daraufhin erscheinenden Formular ein. Übernommen werden diese, wenn Sie die sich dort befindende Schaltfläche Ok bedienen.
   
   Möchten Sie Integrationsbereichsgrenzen mit der Maus verändern, so klicken Sie mit der linken Maustaste in den rechteckig umrahmten Mausfangbereich und bewegen den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts.
    
7. Um sich die Darstellung der Funktion(en) nur innerhalb des festgelegten Integrationsbereichs ausgeben zu lassen, aktivieren Sie das Kontrollkästchen Nur I-Bereich.
    
8. Um Bereichsgrenzen durch Simulationen verändern zu lassen, aktivieren Sie den Kontrollschalter Bereich und bedienen die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. den Wert für die zu verwendende Schrittweite einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop

 

Analytische Ermittlung der Stammfunktionen einer Funktionen in expliziter Form

 
Unter dem Menüpunkt Stammfunktion können Sie sich für Funktionen in expliziter Form eine Stammfunktion symbolisch ausgeben lassen. Dies ist jedoch nur auf einige einfache funktionale Zusammenhänge anwendbar.
 

1. Nach der gemäß den geltenden Syntaxregeln durchgeführten Formulierung der Funktion im Eingabefeld mit der Bezeichnung f1(x) = bzw. f2(x) = wählen Sie den Menüeintrag Stammfunktion.
    
2. Wird die Schaltfläche Ermitteln auf dem Unterformular bedient, so wird eine Stammfunktion der eingegebenen Funktion ermittelt und im entsprechenden Ausgabefeld angezeigt.

 
Ist die Funktionsdeklaration zu komplex um eine Stammfunktion symbolisch ermitteln zu können, so erscheint der Eintrag 'Funktion zu komplex - nicht symbolisch integrierbar' in den Ausgabefeldern.

Durch die Bedienung der dortigen Schaltfläche Schließen kehren Sie wieder zum Unterprogramm zurück.

 
 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• Bereich beschriften: Darstellung der Mausfangpunkte ein-/ausschalten
• Koordinaten: Anzeige der Koordinaten der Mausfangpunkte ein-/ausschalten
• Bereichsmarkierung: Anzeige der Markierung des Integrationsbereichs ein-/ausschalten 

 

 
Bei der Wahl des Registerblatts Funktionen in Polarform können Integrationsberechnungen mit Funktionen, die in Polarform gegeben sind, durchgeführt werden.

Bei Ausführung von Berechnungen für eine Funktion dieser Art werden die Werte folgender Größen innerhalb des festgelegten Winkelintervallbereichs numerisch ermittelt und ausgegeben:
 

• Fläche A (Flächeninhalt) zwischen der Kurve r = f(w) sowie den Ortsvektoren r₁ = f(w₁) und r₂ = f(w₂)
  bzw.
  Fläche A (Flächeninhalt) zwischen der Kurve r = f(φ) sowie den Ortsvektoren r₁ = f(φ₁) und r₂ = f(φ₂)
   
• Bogenlänge s der Kurve
   
• Schwerpunkt der Kurve
• Schwerpunkt der Fläche (Flächenschwerpunkt)

• Volumen/Rotationsvolumen (abs.) V(x) des bei Rotation der Kurve um die x-Achse entstehenden Körpers
• Volumen/Rotationsvolumen (abs.) V(y) des bei Rotation der Kurve um die y-Achse entstehenden Körpers
   
• Mantelfläche/Rotationsfläche (abs.) A(x) des bei Rotation der Kurve um die x-Achse entstehenden Körpers
• Mantelfläche/Rotationsfläche (abs.) A(y) des bei Rotation der Kurve um die y-Achse entstehenden Körpers
   
• Statisches Moment Mx des Kurvenstücks
• Statisches Moment My des Kurvenstücks
• Statisches Moment Mx des Flächenstücks
• Statisches Moment My des Flächenstücks
• Statisches Moment Myz des Drehkörpers

  

 

Ein Polarkoordinatensystem ist ein krummliniges Koordinatensystem. Die Koordinatenlinien, bei welchen die Koordinaten aus konzentrischen Kreisen um den Koordinatenursprung (Pol) und Strahlen, die vom Pol aus radial nach außen verlaufen, bestehen, beschreiben dies. Die Polarkoordinaten eines Punktes (in der Ebene) bestehen aus der Abstandskoordinate r und der Winkelkoordinate φ. Eine in Polarkoordinaten dargestellte Funktion wird durch eine Gleichung der Form r = f(φ) beschrieben. In diesem Programm muss das Zeichen W für den Winkel φ verwendet werden.

 

Übersicht:

 

Bezeichnung in Fachliteratur	Bezeichnung in MathProf
r = f(φ)	r = f(w)

 

Hinweise:

Um sich Funktionen in Polarform in einem Polarkoordinatensystem ausgeben zu lassen, wählen Sie bei der Darstellung dieser unter dem Menüpunkt Einstellungen den Eintrag Auflösung-Skalierungsart und aktivieren die Option Polarkoordinatensystem.
 

 

 
Sollen Integralberechnungen mit Funktionen in Polarform durchgeführt und Zusammenhänge grafisch ausgegeben werden, so gehen Sie wie nachfolgend geschildert vor:
 

1. Definieren Sie die darzustellende Funktion im Eingabefeld mit der Bezeichnung r = f(w) =.
    
2. Legen Sie durch die Eingabe entsprechender Zahlenwerte den Winkelwertebereich fest, über welchen die numerische Integration durchgeführt werden soll (Integration von w1 = und bis w2 =). Voreingestellt ist der Bereich -π ≤ w ≤ π. Standardwerte hierfür können Sie holen, indem Sie das entsprechende Eingabefeld fokussieren und die rechte Maustaste bedienen.
    
3. Definieren Sie mittels dem zur Verfügung stehenden Rollbalken Stützstellen die Anzahl der für die Berechnungen zu verwendenden Stützstellen.
    
4. Nach einer Bedienung der Schaltfläche Berechnen werden die ermittelten Ergebnisse in der zur Verfügung stehenden Listbox ausgegeben.
    
5. Bestimmen Sie durch die Aktivierung des Kontrollschalters Grob, Mittel, Fein oder Sehr fein, mit welcher Auflösung die Darstellung ausgegeben werden soll (voreingestellt: mittel).
    
6. Wählen Sie durch die Eingabe entsprechender Zahlenwerte, über welchen Bereich die grafische Integration durchgeführt werden soll (Darstellungsbereich von w1 = und bis w2 =). Voreingestellt ist der Bereich -π ≤ w ≤ π. Standardwerte hierfür können Sie holen, indem Sie das entsprechende Eingabefeld fokussieren und die rechte Maustaste bedienen.
    
7. Legen Sie durch die Auswahl des relevanten Eintrags aus der Auswahlbox fest, ob eine Flächenmarkierung über den Bereich erfolgen soll, welcher unter Darstellung - Optionen festgelegt wurde, oder ob eine Flächenmarkierung über den Bereich erfolgen soll, welcher unter Einstellungen definiert wurde.
    
8. Bedienen Sie die Schaltfläche Darstellen.

 
 

 
Bei der Wahl des Registerblatts Funktionen in Parameterform können Integralberechnungen mit Funktionen, die in Parameterform gegeben sind, durchgeführt werden.

Bei Durchführung einer Berechnung für Funktionen der Form x = f(k) und y = g(k) werden die Werte folgender Größen innerhalb des festgelegten Parameterintervallbereichs numerisch ermittelt und ausgegeben:
 

• Fläche A zwischen der Kurve x = f(k) und y =g(k) sowie den Ortsvektoren 0P1 und 0P2
   
• Bogenlänge s der Kurve

• Volumen/Rotationsvolumen (abs.) V(x) des bei Rotation der Kurve um die x-Achse entstehenden Körpers
• Volumen/Rotationsvolumen (abs.) V(y) des bei Rotation der Kurve um die y-Achse entstehenden Körpers
   
• Mantelfläche/Rotationsfläche (abs.) A(x) des bei Rotation der Kurve um die x-Achse entstehenden Körpers
• Mantelfläche/Rotationsfläche (abs.) A(y) des bei Rotation der Kurve um die y-Achse entstehenden Körpers
   
• Statisches Moment Mx des Kurvenstücks
• Statisches Moment My des Kurvenstücks
• Statisches Moment Mx des Flächenstücks
• Statisches Moment My des Flächenstücks
• Statisches Moment Myz des Drehkörpers
   
• Schwerpunkt der Kurve

 

Bei der Darstellung von Funktionen in Parameterform werden die Koordinaten der Kurvenpunkte durch zwei Gleichungen ermittelt. Die Werte (Koordinaten) für x und y hängen von einem reellwertigen Parameter k ab, welcher einen definierbaren Wertebereich durchläuft. Das Symbol, welches diesen Parameter beschreibt, ist in diesem Programm auf K festgelegt. Funktionen dieser Art müssen (bei Verwendung dieses Parameters) bei deren Definition deshalb stets das Zeichen K enthalten.

Übersicht:

 

Bezeichnung in Fachliteratur	Bezeichnung in MathProf
x = f(t)  y = g(t)	x = f(k)  y = g(k)

 

 

Sollen Integralberechnungen mit Funktionen in Parameterform durchgeführt und Zusammenhänge grafisch dargestellt werden, so gehen Sie wie nachfolgend geschildert vor:
 

1. Definieren Sie die Funktionsterme in den zur Verfügung stehenden Eingabefeldern mit den Bezeichnungen x = f(k) = und y = g(k) =.
    
2. Legen Sie durch die Eingabe entsprechender Zahlenwerte den Untersuchungsbereich für den Funktionsparameter K fest, innerhalb dessen die numerische Analyse durchgeführt werden soll (Integration von k1 = und bis k2 =) (voreingestellt: -π ≤ k ≤ π). Standardwerte hierfür können Sie holen, indem Sie das entsprechende Eingabefeld fokussieren und die rechte Maustaste bedienen.
    
3. Definieren Sie mittels dem zur Verfügung stehenden Rollbalken Stützstellen die Anzahl der für die Berechnungen zu verwendenden Stützstellen.
    
4. Nach einer Bedienung der Schaltfläche Berechnen werden die ermittelten Ergebnisse in der zur Verfügung stehenden Listbox ausgegeben.
    
5. Bestimmen Sie durch die Aktivierung des Kontrollschalters Grob, Mittel, Fein oder Sehr fein, mit welcher Auflösung die Darstellung ausgegeben werden soll (voreingestellt: mittel).
    
6. Wählen Sie durch die Eingabe entsprechender Zahlenwerte, über welchen Bereich die grafische Integration durchgeführt werden soll (Darstellungsbereich von k1 = und bis k2 =). Voreingestellt ist der Bereich -π ≤ k ≤; π. Standardwerte hierfür können Sie holen, indem Sie das entsprechende Eingabefeld fokussieren und die rechte Maustaste bedienen.
    
7. Legen Sie durch die Auswahl des entsprechenden Eintrags aus der Auswahlbox fest, ob eine Flächenmarkierung über den Bereich erfolgen soll, welcher unter Darstellung - Optionen festgelegt wurde, oder ob eine Flächenmarkierung über den Bereich erfolgen soll, welcher unter Einstellungen definiert wurde.
    
8. Bedienen Sie die Schaltfläche Darstellen.

Hinweis:

Es wird die Fläche zwischen der Kurve x = f(k) und y = g(k) und den vom Koordinatenursprung ausgehenden Ortsvektoren 0P1 und 0P2 (mit P1 bei k1 und P2 bei k2) gemäß der Leibnitzschen Sektorformel markiert. Auch die Ermittlung der Berechnungsergebnisse erfolgt nach diesem Verfahren.
 

 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Die numerische Errechnung der Ergebnisse wird durch die Anzahl vorgegebener Stützstellen beeinflusst. Je mehr Stützstellen verwendet werden, desto genauer werden die Ergebnisse. Dennoch gilt es zu beachten, dass die Berechnungszeit durch eine Erhöhung der Stützstellenanzahl exponentiell steigt. Den Abbruch der Durchführung von Berechnungen können Sie durch eine Bedienung der Taste ESC veranlassen.

Prinzipiell sollten diese numerischen Integrationsverfahren nur bei stetigen Funktionen verwendet werden, bzw. bei unstetigen Funktionen nur innerhalb derer stetiger Wertebereiche, da es ansonsten zu Verfälschungen der Ergebnisse kommen kann. Die Genauigkeit bei der Errechnung der Bogenlänge, Mantelfläche und stat. Momente hängt von der Differenzierbarkeit der Funktion ab. Somit kann es hierbei zu erheblichen Abweichungen kommen. Der Schwerpunkt einer Fläche kann nur errechnet werden, wenn zwischen den Intervallgrenzen des Integrationsbereichs kein Vorzeichenwechsel auftritt. (näheres siehe Fachliteratur)
 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Integralrechnung - Interaktiv

Ober- und Untersummen

Ober- und Untersummen - Interaktiv

Integrationsmethoden

Mathematische Funktionen I

Funktionen in Parameterform

Funktionen in Polarform

Rotation von Kurven in kartesischer Form um die X-Achse (3D)

Rotation von Kurven in Parameterform um die X-Achse (3D)

 

 

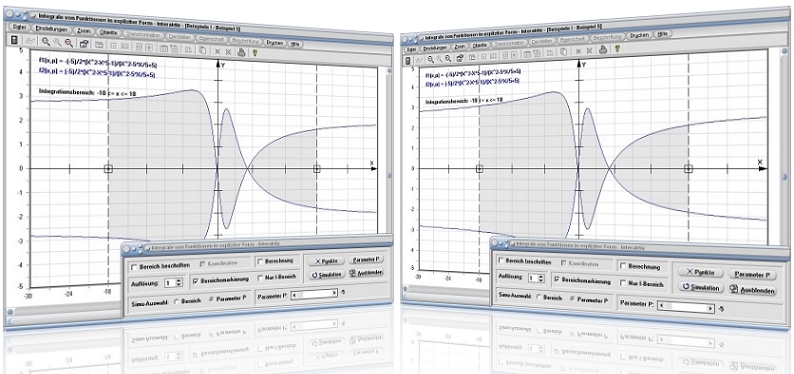
Beispiel 1 - Integralrechnung (Flächenberechnung) mit einer Funktion in expliziter Form:

Untersuchung der expliziten Funktion y = f(x) = sin(x)-0,5 im Integrationsbereich von x₁ = 0 bis x₂ = 2. Es gilt u.a., die zwischen der Kurve und der Abszisse eingeschlossene Fläche ermitteln zu lassen.

Vorgehensweise und Lösung:

Wählen Sie das Registerblatt Funktionen in expliziter Form und legen Sie durch die Positionierung des dafür vorgesehenen Rollbalkens eine Stützstellenanzahl von ca. 100000 fest.

Nach Eingabe der Zahlenwerte 0 und 2 in die Felder Integration von x1 = und bis x2 =, sowie der Definition des Funktionsterms (Integranden) SIN(X)-0,5 im Eingabefeld f1(x) =, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse:

Fläche orientiert A(o): 0,416 FE (Fläche zwischen der Funktion und der x-Achse)
Fläche absolut A(a): 0,672 FE (Betrag der Fläche, unabhängig davon ob Flächensegmente sich oberhalb, oder unterhalb der Abszissenachse befinden)

 

Bogenlänge der Kurve s: 2,352 LE

 

Schwerpunkt der Kurve: SK (0,93 / 0,17)

 

Volumen (abs.) des bei Rotation der Kurve um die X-Achse entstehenden Körpers (Rotationsvolumen): V(x) = 0,858 VE

Volumen (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers, wenn Fläche unter der Kurve bzgl. der x-Achse verwendet wird (Rotationsvolumen): V(y) = 2,453 VE

Volumen (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers, wenn Fläche unter der Kurve bzgl. der y-Achse verwendet wird (Rotationsvolumen): V(y) = 4,936 VE

 

Mantelfläche (abs.) des bei Rotation der Kurve um die x-Achse entstehenden Körpers: A(x) = 4,759 FE

Mantelfläche (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers: A(y) = 13,739 FE

 

Statisches Moment des Kurvenstücks bzgl. x-Achse: Mx = 0,4

Statisches Moment des Kurvenstücks bzgl. y-Achse: My = 2,187

Statisches Moment des Flächenstücks bzgl. x-Achse: Mx = 0,137

Statisches Moment des Flächenstücks bzgl. y-Achse: My = 0,742
 

Beispiel 2 - Integralrechnung (Flächenberechnung) mit zwei Funktionen in expliziter Form:

Untersuchung zweier explizit definierter Funktionen:
 

f1(x) = sin(x)-0,5

f2(x) = x²-1

 

Es gilt u.a., die zwischen den Kurven f1(x) und f2(x) eingeschlossene Fläche im Bereich von x₁ = -2 bis x₂ = 1 ermitteln zu lassen (Differenzfunktion).
 

Vorgehensweise und Lösung
 

Wählen Sie das Registerblatt Funktionen in expliziter Form und legen Sie durch die Positionierung des dafür vorgesehenen Rollbalkens eine Stützstellenanzahl von ca. 100000 fest. Aktivieren Sie die beiden zur Verfügung stehenden Kontrollkästchen bei den Eingabefeldern.

Nach Eingabe der Zahlenwerte -2 und 1 in die Felder Integration von x1 = und bis x2 =, sowie der Definition der Funktionsterme SIN(X)-0,5 und X^2-1 in den Eingabefeldern f1(x) = und f2(x) =, gibt das Programm nach einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse aus:

Fläche absolut A(a): 3,91 FE (Betrag der Summe aller zwischen beiden Funktionen eingeschlossenen Flächensegmente)

Fläche orientiert A(o): -2,456 FE (orientierte Fläche zwischen beiden Funktion)

 

Ferner wird für Funktion f1(x) ausgegeben:

 

Bogenlänge der Kurve s: 3,663 LE

Schwerpunkt der Kurve: SK (-0,425 / -0,771)

 

Volumen (abs.) des bei Rotation der Kurve um die X-Achse entstehenden Körpers (Rotationsvolumen): V(x) = 9,954 VE

Volumen (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers, wenn Fläche unter der Kurve bzgl. der x-Achse verwendet wird (Rotationsvolumen): V(y) = 3,204 VE

Volumen (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers, wenn Fläche unter der Kurve bzgl. der y-Achse verwendet wird (Rotationsvolumen): V(y) = 17,824 VE

 

Mantelfläche (abs.) des bei Rotation der Kurve um die x-Achse entstehenden Körpers: A(x) = 19,073 FE

Mantelfläche (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers: A(y) = 17,706 FE

 

Statisches Moment des Kurvenstücks bzgl. x-Achse: Mx = -2,825

Statisches Moment des Kurvenstücks bzgl. y-Achse: My = -1,555

Statisches Moment des Flächenstücks bzgl. x-Achse: Mx = 1,584

Statisches Moment des Flächenstücks bzgl. y-Achse: My = 2,793
 

Beispiel 3 - Integralrechnung (Flächenberechnung) mit einer Funktion in Polarform:

Die Funktion in Polarform r = f(φ) = 1+cos(φ) beschreibt über ein Intervall von 0 ≤ φ ≤ 2π eine Kardioide. Es gilt u.a., die von der Kurve über diesen Bereich eingeschlossene Fläche, ermitteln zu lassen.

Vorgehensweise und Lösung:

Wählen Sie das Registerblatt Funktionen in Polarform und legen Sie durch die Positionierung des dafür vorgesehenen Rollbalkens eine Stützstellenanzahl von ca. 100000 fest. Selektieren Sie den Eintrag Standard aus der Auswahlbox mit der Bezeichnung Art.

Nach Eingabe der Zahlenwerte 0 und 6,28318 in die Felder Integration von w1 = und bis w2 = (durch Bedienung der rechten Maustaste, während Eingabefeld fokussiert ist), sowie der Eingabe der Zeichenfolge 1+COS(W) in das dafür vorgesehene Feld mit der Bezeichnung r = f(w) =, gibt das Programm nach einer Bedienung der Schaltfläche Berechnen aus:

Fläche: A = 4,712 FE

Sollte diese Aufgabe algebraisch gelöst werden, so führt der Ansatz zur Ermittlung dieser Fläche über eine Mehrfachintegration

zu dem Ergebnis A = 3/2π FE. Hieraus wird ersichtlich, dass sich das Ergebnis der numerischen Berechnung bei der Festlegung einer relativ hohen Anzahl von Stützstellen dem wahren Wert sehr gut nähert.

Zudem wird ausgegeben:

Bogenlänge der Kurve: s = 8 LE

 

Volumen (abs.) des bei Rotation der Kurve um die X-Achse entstehenden Körpers (Rotationsvolumen): V(x) = 16,821 VE

Volumen (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers (Rotationsvolumen): V(y) = 25,444 VE

 

Mantelfläche (abs.) des bei Rotation der Kurve um die x-Achse entstehenden Körpers (Rotationsfläche): A(x) = 40,212 FE

Mantelfläche (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers (Rotationsfläche): A(y) = 45,091 FE

 

Statisches Moment des Kurvenstücks bzgl. x-Achse: Mx = 0

Statisches Moment des Kurvenstücks bzgl. y-Achse: My = 6,4

Statisches Moment des Flächenstücks bzgl. x-Achse: Mx = 0

Statisches Moment des Flächenstücks bzgl. y-Achse: My = 3,927

Statisches Moment des Körpers bei Rotation um x-Achse: Myz = 0

 

Schwerpunkt der Kurve: SK (0,8 / 0)

Schwerpunkt der Fläche: SF (0,833 / 0)
 

Beispiel 4 - Integralrechnung (Flächenberechnung) mit Funktionen in Parameterform:

Die Funktionen x = f(k) = 8·cos(k) und y = f(k) = 3·sin(k) beschreiben über einen Darstellungsbereich von 0 ≤ k ≤ π eine Ellipse mit den Halbachsen a = 8 und b = 3. Es gilt u.a., die von der Kurve über diesen Bereich eingeschlossene Fläche ermitteln zu lassen.

Vorgehensweise und Lösung:

Wählen Sie das Registerblatt Funktionen in Parameterform und legen Sie durch die Positionierung des dafür vorgesehenen Rollbalkens eine Stützstellenanzahl von ca. 100000 fest. Selektieren Sie den Eintrag Kartesisch aus der Auswahlbox mit der Bezeichnung Art.

Nach einer Definition der Funktionsterme durch die Eingabe der Zeichenfolgen 8*COS(K) und 3*SIN(K) in die dafür vorgesehenen Felder x = f(k) = und y = g(k) =, der Eingabe der Zahlenwerte 0 und 3,14159 in die Felder Integration von k1 = und bis k2 = (durch Bedienung der rechten Maustaste, während Eingabefeld fokussiert ist), führt die Ausführung der erforderlichen Berechnungen bei bei einer eingestellten Stützstellenzahl von ca. 100000 zu den Ergebnissen:

Fläche: A = 37,699 FE  (entspricht der Hälfte des Werts, der bei der Berechnung der Fläche einer Ellipse über die Gleichung A = πab ermittelt wird)

 

Bogenlänge der Kurve: s = 18,183 LE

 

Volumen (abs.) des bei Rotation der Kurve um die X-Achse entstehenden Körpers (Rotationsvolumen): V(x) = 301,593 VE

Volumen (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers (Ellipsoid) (Rotationsvolumen): V(y) = 804,24 VE

 

Mantelfläche (abs.) des bei Rotation der Kurve um die x-Achse entstehenden Körpers (Rotationsfläche): A(x) = 501,967 FE

Mantelfläche (abs.) des bei Rotation der Kurve um die y-Achse entstehenden Körpers (Rotationsfläche): A(y) = 249,537 FE (Ellipsoid)

 

Statisches Moment des Kurvenstücks bzgl. x-Achse: Mx = 39,175

Statisches Moment des Kurvenstücks bzgl. y-Achse: My = 0

Statisches Moment des Flächenstücks bzgl. x-Achse: Mx = -48

Statisches Moment des Flächenstücks bzgl. y-Achse: My = 0

Statisches Moment des Körpers bei Rotation um x-Achse: Myz = 0

 

Schwerpunkt der Kurve: S (0 / 2,184)

 

Hinweis:

Die Berechnungsergebnisse bei Funktionen in Parameterform beziehen sich auf die Fläche der Kurve x = f(k) und y = g(k) und den vom Koordinatenursprung ausgehenden Ortsvektoren 0P1 und 0P2 (mit P1 bei k1 und P2 bei k2), gemäß der Leibnitzschen Sektorenformel.
 
 

 

Grafische Darstellung - Funktionen in expliziter Form - Beispiel 1


Grafische Darstellung - Funktionen in expliziter Form - Beispiel 2


Grafische Darstellung - Funktionen in Polarform - Beispiel 1


Grafische Darstellung - Funktionen in Parameterform - Beispiel 1
 

Formeln zur Integralrechnung mit Funktionen in expliziter Form

 
Die Formeln zur Ermittlung der vom Programm ausgegebenen Werte für Funktionen in expliziter Form sind nachfolgend (in von oben abweichender Darstellungsform) angegeben.

Eine Funktion in expliziter Form wird wie folgt beschrieben: y =  f(x)

 

Flächeninhalt:

 

 

Rotationsvolumen bei Rotation um x-Achse:

 

Rotationsvolumen bei Rotation um y-Achse:

 

 

bzw.:

 

 

Mantelfläche (Rotationsfläche) bei Rotation um x-Achse:

 

 

Mantelfläche (Rotationsfläche) bei Rotation um y-Achse:

 

 

Bogenlänge (Länge des Kurvenstücks):

 

 

bzw.:

 

 

Statisches Moment des Kurvenstücks bzgl. x-Achse:

 

 

Statisches Moment des Kurvenstücks bzgl. y-Achse:

 

 

Statisches Moment des Flächenstücks bzgl. x-Achse:

 

 

Statisches Moment des Flächenstücks bzgl. y-Achse:

 

 

Statisches Moment des Rotationskörpers bei Rotation um x-Achse:

 

 

Schwerpunkt der homogenen Kurve:

 

   
 

Schwerpunkt der homogenen Fläche:

 

 

Schwerpunkt des homogenen Rotationskörpers:

 

   

 

 

Formeln zur Integralrechnung mit Funktionen in Polarform

 
Die Formeln zur Ermittlung der vom Programm ausgegebenen Werte für Funktionen in Polarform sind nachfolgend angegeben.

Eine Funktion in Polarform wird wie folgt beschrieben: r = f(φ)

 

Fläche:

 

 

Rotationsvolumen bei Rotation um x-Achse:

 

 

Rotationsvolumen bei Rotation um y-Achse:

 

 

Bogenlänge (Länge des Kurvenstücks):

 

 

bzw.

 

 

Mantelfläche (Rotationsfläche) bei Rotation um x-Achse:

 

 

 

Mantelfläche (Rotationsfläche) bei Rotation um y-Achse:

 

 

 

Statisches Moment des Kurvenstücks bzgl. x-Achse:

 

 

Statisches Moment des Kurvenstücks bzgl. y-Achse:

 

 

Statisches Moment des Flächenstücks bzgl. x-Achse:

 

 

Statisches Moment des Flächenstücks bzgl. y-Achse:

 

 

Statisches Moment des Rotationskörpers bei Rotation um x-Achse:

 

 

Schwerpunkt der homogenen Kurve:

 

   

Schwerpunkt der homogenen Fläche:

 

 

Schwerpunkt des homogenen Rotationskörpers:

 

   

 

 

Formeln zur Integralrechnung mit Funktionen in Parameterform

 
Die Formeln zur Ermittlung der vom Programm ausgegebenen Werte für Funktionen in Parameterform sind nachfolgend (in von oben abweichender Darstellungsform)

Funktionen in Parameterform werden wie folgt beschrieben:

x = φ (k)
y = φ (k)

 

 

Fläche zwischen der Kurve und den Ortsvektoren 0P1 und 0P2:

 

 

Die Angabe zum Flächeninhalt bezieht sich auf die Fläche der Kurve x = f(k) und y = g(k) und den vom Koordinatenursprung ausgehenden Ortsvektoren 0P1 und 0P2 (mit P1 bei k1 und P2 bei k2), gemäß der Leibnitzschen Sektorenformel.

 

Rotationsvolumen bei Rotation um x-Achse:
 

 

Rotationsvolumen bei Rotation um y-Achse:
 

 

Bogenlänge (Länge des Kurvenstücks):

 

 

Mantelfläche (Rotationsfläche) bei Rotation um x-Achse:

 

 

Mantelfläche (Rotationsfläche) bei Rotation um y-Achse:

 

 

Statisches Moment des Kurvenstücks bzgl. x-Achse:

 

 

Statisches Moment des Kurvenstücks bzgl. y-Achse:

 

 

Statisches Moment des Flächenstücks bzgl. x-Achse:

 

 

Statisches Moment des Flächenstücks bzgl. y-Achse:

 

 

Statisches Moment des Rotationskörpers bei Rotation um x-Achse:

 

 

Schwerpunkt der homogenen Kurve:

 

   
 

Schwerpunkt der homogenen Fläche:

 

 

Schwerpunkt des homogenen Rotationskörpers:

 

   

 

  

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Integralrechnung, Wikipedia - Mantelfläche und Wikipedia - Geometrischer Schwerpunkt zu finden.

 

 

 

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

 

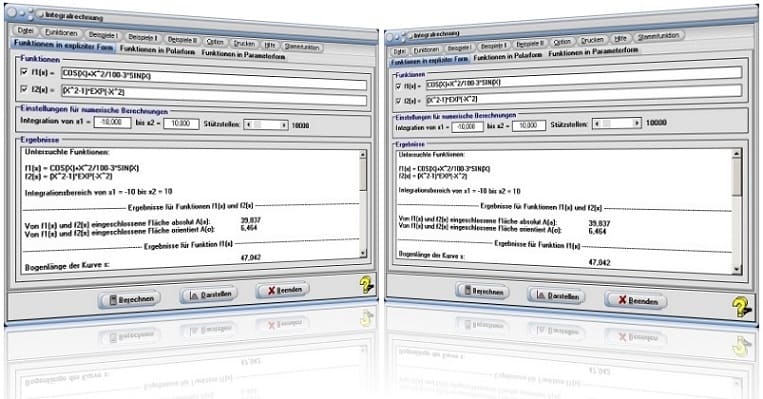
Startfenster des Unterprogramms Integralrechung
 

MathProf 5.0 - Unterprogramm Kurvendiskussion - Interaktiv

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---