MathProf - Stichprobe - Skala - Häufigkeit - Merkmale - Niveau

     

 

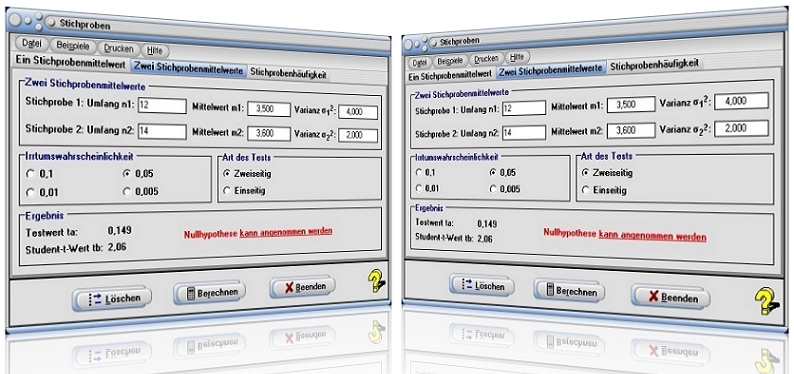
Modul Stichproben

---

 
Im kleinen Programmmodul [Stochastik] - Stichproben können Untersuchungen mit normalverteilten Stichprobenwerten durchgeführt werden.

 

 

 

• Test eines Stichprobenmittelwerts einer normalverteilten Grundgesamtheit

• Test von zwei Stichprobenmittelwerten einer normalverteilten Grundgesamtheit

• Test einer Stichprobenhäufigkeit

   
Die Gesamtheit statistisch untersuchter Gegenstände, Individuen oder Objekte wird als Grundgesamtheit bezeichnet. Teilmengen der Grundgesamtheit werden Stichproben genannt. Eine Stichprobe stellt eine Teilmenge aller Analyseeinheiten dar, die das Ziel hat relevante Eigenschaften einer Grundgesamtheit möglichst exakt abzubilden. Mit Hilfe einer Stichprobenziehung wird beabsichtigt, von bekannten Kennwerten einer Stichprobe auf unbekannte Kennwerte der Grundgesamtheit zu schließen.
 
Die in einer Stichprobe erfassten Daten sind die Beobachtungswerte. Die Eigenschaften der Elemente einer Stichprobe hießen Merkmale.

Statistische Erhebung: Bei einer statistischen Erhebung handelt es sich um die Erfassung, Auswertung und Darstellung statistisch erfasster Daten. Deren Durchführung erfolgt durch Zählung, Messung oder Befragung. Grundlage einer derartigen Untersuchung ist eine Menge von Elementen von welchen ein Merkmal oder mehrere Merkmalskombinationen analysiert werden.

Eine statistische Vollerhebung (Totalerhebung) umfasst bei einer statistischen Analyse die Einbeziehung und Untersuchung aller statistischen Einheiten einer Grundgesamtheit.

Wird lediglich ein Teil der statistischen Einheiten einer Grundgesamtheit zur Auswertung einbezogen, so handelt es sich um eine Teilerhebung.
 
Verschiedene Ausprägungen in denen eine Eigenschaft vorkommt heißen Merkmalsausprägungen. Gruppenweise zusammengefasste Merkmalsausprägungen bilden eine Merkmalsklasse. Merkmale dieser Art werden in Skalen eingeteilt. Merkmalsausprägungen können in Datenklassen (Kategorien) zusammengefasst werden, um deren Darstellung übersichtlicher und benutzerfreundlicher zu gestalten.

Metrische Skalen: Eine metrische Skala bzw. Kardinalskala macht Aussagen über den Betrag der Differenzen zwischen zwei Klassen. Mit Hilfe einer metrischen Skala lassen sich Merkmalsausprägungen ordnen sowie deren Abstände berechnen. Merkmale mit metrischer Skala treten als diskrete Zahlenwerte oder in Form von Zahlenintervallen auf. Als metrisch skaliert werden Daten bezeichnet, die eine natürliche Reihenfolge besitzen und deren Abstände zwischen den Merkmalsausprägungen eindeutig definiert sind.
 
Eine Nominalskala dient der Zuordnung von Merkmalsausprägungen die lediglich derer Kennzeichnung dienen. Sie hat lediglich die Bedingung zu erfüllen, dass Daten (Objekte bzw. Merkmalsträger) hierdurch eine eindeutige Zuordnung in Klassen (Kategorien) ermöglicht wird. Eine derartige Klassifizierung in eine Kategorie kann beispielsweise durch die Zuordnung von Zahlen zu Formen erfolgen, wie z.B. 1 zu rund, 2 zu eckig, 3 zu oval etc. und wird als Nominalskalierung bezeichnet.Weitere Beziehungen zwischen einzelnen Klassen bestehen nicht und ein Vergleich einzelner Klassen untereinander kann nicht durchgeführt werden. Daten die nominalskaliert sind, sind Daten, die sich nicht  in eine natürliche Reihenfolge bringen lassen.

Eine Ordinalskala oder Rangskala ist eine Zuordnung der Merkmalsträger, deren Ausprägungen eine eindeutige Rangordnung besitzen, in verschiedene Kategorien. Sie teilt Variablen mit Ausprägungen zwischen welchen eine Rangordnung besteht in Bereiche ein. Hinsichtlich der Abstände zwischen einzelnen Werten lassen sich jedoch keine konkreten zahlenmäßien Aussagen machen. Beispiele hierfür sind Schulnoten, denn der Abstand zwischen einer 1 und einer 2 bedeutet nicht dasselbe wie der Unterschied zwischen einer 4 und einer 5. Daten die ordinalskaliert sind enthalten Nominalinformationen wie auch Informationen über die Reihung der Variablenwerte sowie eine endliche Zahl von möglichen Ausprägungen.
 
Eine Intervallskala (Einheitsskala) ist eine metrische Skala, welche eine Aussage hinsichtlich der absoluten Abstände (Differenzen) zwischen einzelnen Werten (Daten) zulässt. Eine Skala dieser Art besitzt jedoch keinen natürlichen Nullpunkt sowie keine natürliche Einheit. Beispielsweise beträgt die Differenz zwischen den Temperaturen -25°C und -5°C ebenso wie der Abstand zwischen 20°C und 40°C exakt 10 Grad Celsius. Es kann jedoch nicht die Ausssage gemacht werden, dass die Temperatur 20"C das Doppelte der Temperatur 40°C bedeutet, da diese Temperaturskala einen willkürlich gewählten Nullpunkt besitzt. Eine Skala heißt intervallskaliert, wenn die Distanzen zwischen den Werten der Skala stets gleich groß sind.
 
Eine Verhältnisskala (Ratioskala) verfügt über einen natürlichen Nullpunkt, jedoch über keine natürliche Maßeinheit. Beispiele für ratioskalierte Merkmale sind Alter, Grösse, Gewicht oder Länge. Bei ratioskalierten Merkmale lassen sich Aussagen über die Verhältnisse non Merkmalsausprägungen machen. Beispielsweise ist eine Person die eine Körpergröße von 200 cm besitzt doppelt so groß wie ein 100 cm großes Kind. Daten die verhältnisskaliert (ratioskaliert) sind besitzen im Gegensatz zu intervallskalierten Daten einen absoluten Nullpunkt.
 
Eine Absolutskala besitzt einen natürlichen Nullpunkt sowie eine natürliche Maßeinheit. Die Merkmalsausprägungen werden in Form von Zahlenwerten dargestellt. Beispiele hierfür sind Stückzahlen von Gegenständen oder Personenzahlen.

Qualitatives Merkmal: Merkmale mit Nominalskala und Ordinalskala werden als qualitative Merkmale bezeichnet. Beispiele für qualtitative (metrische) Merkmale sind Geschlecht, Familienstand, Religion.

Skalenniveaus (Messniveaus): Das Skalenniveau (Messniveau) ist eine wichtige Eigenschaft von Merkmalen und Variablen. Es bestimmt welche mathematischen Operationen zulässig sind und damit welche möglichen statistischen Tests mit Merkmalen und Variablen durchführbar sind. Das Skalenniveau einer Variable kann metrisch, nominal oder ordinal sein. Es erteilt keine Auskunft darüber, ob eine Variable diskret oder stetig ist.
 
Quantitatives Merkmal (metrisches Merkmal): Merkmale mit metrischer Skala heißen quantitative Merkmale oder metrische Merkmale. Beispiele für quantitative Merkmale sind Alter, Größe, Gewicht, Temperatur.
 
Dichotome Merkmale: Als dichotomes Merkmal wird ein Merkmal bezeichnet dessen Ausprägungen genau zwei unterschiedliche Werte annehmen kann. Beispiel für ein diskretes Merkmal ist 'Kopf oder Zahl' beim Münzwurf.

Stetige Merkmale: Als stetiges Merkmal wird ein Merkmal bezeichnet, welches überabzählbar viele Werte besitzen kann. Es muss über eine unendliche Zahl an Elementen verfügen und somit dem Bereich der reellen Zahlen zuzuordnen sein. Beispiele für stetige Merkmale sind Gewicht, Zeitintervall, Nettomiete.

Diskrete Merkmale: Als diskretes Merkmal wird ein Merkmal bezeichnet dessen Ausprägungen nur ganzzahlige Werte annehmen kann. Beispiele für diskrete Merkmale sind Schulnoten, Anzahl Beschäftigter.

Häufigkeitstabellen - Urlisten - Absolute Häufigkeiten: Als Urliste wird in der Statistik die ursprüngliche Aufzeichnung der Beobachtungs- bzw. Messwerte bezeichnet. Die Anzahl, mit welcher eine Merkmalsausprägung a_i in einer Urliste auftritt wird als absolute Häufigkeit von a_i bezeichnet. Ihre Darstellung erfolgt in einer Häufigkeitstabelle.

Unter dem Begriff Spannweite wird die Differenz zwischen dem kleinsten und dem größten Wert einer geordneten Datenreihe verstanden.

Relative Häufigkeiten: Der Quotient, welcher sich aus der absoluten Häufigkeit a_i und der Anzahl n aller Beobachtungswerte ergibt, heißt relative Häufigkeit. Sie errechnet sich wie folgt:



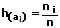
Beispiel absolute Häufigkeit n_i:
 

Merkmalsausprägung ai	a1 = A	a2 = B	a3 = C	a4 = D	a5 = E
Absolute Häufigkeit ni	8	9	5	7	6

 
Beispiel relative Häufigkeit h(a_i):
 

ai	A	B	C	D	E
ni	8	9	5	7	6
h(ai)	8/36 = 0,222...	9/36 = 0,25	5/36 = 0,1388...	7/36 = 0,1944...	6/36 = 0,166...

 

Die grafische Darstellung von Häufigkeiten erfolgt in Diagrammen.




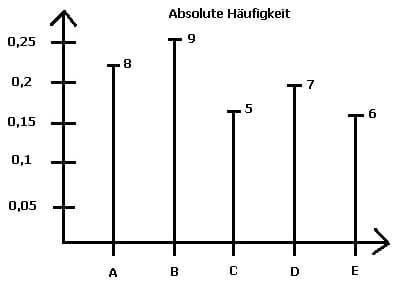
Bsp. 1: Grafische Darstellung der absoluten Häufigkeit in einem Säulendiagramm.




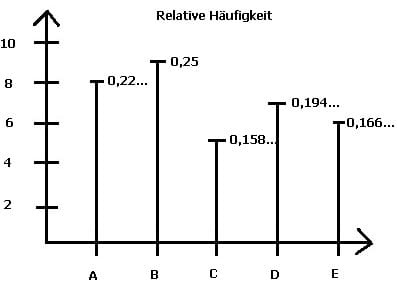
Bsp. 2: Grafische Darstellung der relativen Häufigkeit in einem Säulendiagramm.
   
 
Als Stichprobenumfang oder Stichprobengröße wird die Anzahl ausgewählte Objekte aus einer angegebenen Menge, der Grundgesamtheit, bezeichnet.

Das Signifikanzniveau beschreibt die größte Wahrscheinlichkeit, dass eine Nullhypothese fälschlicherweise Weise abgelehnt wird.

Das Stichprobenmittel (Stichprobenmittelwert oder empirischer Mittelwert oder zufälliges arithmetisches Mittel) ist ein arithmetischer Mittelwert und der Erwartungswert der empirischen Verteilung.

Zentraler Grenzwertsatz: Der zentrale Grenzwertsatz ist ein bedeutender Satz der Wahrscheinlichkeitstheorie. Er besagt, dass sich die Summe sehr vieler unabhängiger identisch verteilter Zufallsvariablen einer Verteilungsart bei wachsendem Umfang an durchgeführten Stichproben approximativ der Normalverteilung nähert.

Empirische Varianz: Als empirische Varianz wird die mittlere quadratische Abweichung gemessener Werte eines Zufallsexperiments von einem empirischen Mittelwert bezeichnet. Sie wird verwendet, wenn lediglich der Teil einer Grundgesamtheit bekannt ist und trägt auch die Bezeichnungen empirische Stichprobenvarianz, empirische Varianz oder Stichprobenvarianz.
 
Die beurteilende Statistik zieht mit Hilfe statistischer Analysen Rückschlüsse auf den Einfluss von Größen wie Erwartungswert oder Wahrscheinlichkeit. Basis dieser Analysen sind Stichprobenanalysen und Hypethesentests.

Statistische Signifikanz: Als statistisch signifikant wird das Ergebnis eines statistischen Tests bezeichnet, wenn Daten durchgeführter Stichproben so stark von einer vorher festgelegten Annahme abweichen, dass diese gemäß einer vorher festgelegten Regel verworfen wird.

Deskriptive Statistik (beschreibende Statistik): Mit Hilfe einer deskriptiven (beschreibenden) Statistik werden ein Datensatz sowie dessen Eigenschaften beschrieben. Hierbei handelt es sich häufig um eine Stichprobe emprischer Daten.

Als Zufallsstichprobe (Zufallsauswahl oder zufällige Stichprobe) wird eine Stichprobe aus einer Grundgesamtheit bezeichnet, die mit Hilfe eines speziellen Auswahlverfahrens entnommen wird.

Überzufälligkeit: Als überzufällig wird in der Statistik ein Zusammenhang beschrieben, dessen nachgewiesene Bedeutung ausreichend hoch ist, um nicht mehr als Zufall zu gelten, jedoch nicht so eindeutig erscheint wie eine direkte Kausalität.

Die Losgröße bezeichnet eine Menge von Produkten (Teilen), die direkt aufeinanderfolgend und ohne Unterbrechung in der Fertigung produziert wird.

Statistischer Test - Statistische Tests: Ein statistischer Test dient dazu, anhand durchgeführter Beobachtungen eine begründete Entscheidung hinsichtlich der Gültigkeit oder Ungültigkeit einer Hypothese zu treffen. Statistische Tests werden durchgeführt, wenn mit Hilfe erhobener Daten Rückschlüsse auf eine Grundgesamtheit nachgewiesen werden sollen. Sie dienen dazu mittels durchgeführter Beobachtungen eine begründete Entscheidung hinsichtlich der Gültigkeit oder Ungültigkeit einer zugrundeliegenden Hypothese zu treffen.

Linksseitiger Test: Bei einem linksseitigen Test befindet sich der Ablehnungsbereich links.
Rechtsseitiger Test: Bei einem rechtsseitigen Test befindet sich der Ablehnungsbereich rechts.

Vorzeichentest: Der Vorzeichentest wird angewandt, wenn die Voraussetzungen zur Durchführung eines t-Tests nicht erfüllt sind. Es ermöglicht es zu prüfen, ob sich die Maße des Gipfels einer Verteilung von zwei abhängigen Stichproben unterscheiden. Vorausgesetzt wird die Abhängigkeit der Stichproben, der Gruppen und der Bedingungen sowie ein ordinales Skalenniveau.

Häufigkeit: Mit dem Begriff Häufigkeit wird die Anzahl erfolgter Ereignisse und somit das Ergebnis eines Zählvorgangs bezeichnet.

Häufigkeitstabelle: Eine Häufigkeitstabelle ist die tabellarische Auflistung untersuchter Merkmale sowie der relativen und der absoluten Häufigkeiten ihres Erscheinens.

Statistische Wahrscheinlichkeit: Die statistische Wahrscheinlichkeit ist ein Maß der Erwartung für ein unsicheres Ereignis. Sie beschreibt die relative Häufigkeit zukünftiger Ereignisse, die von einem zufällig eintretenden Prozess bestimmt werden.

Binomialtest: Als Binomialtest wird ein statistischer Test bezeichnet, bei dem die Teststatistik in binomialverteilter Form vorliegt. Er wird angewandt, um Hypothesen über Merkmale zu prüfen, die in der Lage sind exakt zwei Ausprägungen anzunehmen.

Stichprobenauswahl: Als Stichprobenauswahl wird die Selektion von zu untersuchenden Personen oder Objekten bezeichnet, die durch theoretische und praktische Betrachtungen getragen wird.

Erwartungswert: Beim Erwartungswert handelt es sich um einen endlichen Wert der den Mittelwert einer Zufallsgröße (die Zahl) beschreibt, die diese durchschnittlich annimmt.

Stichprobenfehler: Wenn die korrekt durchgeführte Entnahme einer Stichprobe aus einer Grundgesamtheit dazu führt, dass die Stichprobe ein nicht repräsentatives Abbild der Grundgesamtheit darstellt, so wird von einem Stichprobenfehler gesprochen.

Zufällige Fehler (Zufallsfehler): Fehler dieser Art entstehen durch zufällige auftretende Ereignisse oder Prozesse die sich während dem Messen ereignen. Sie werden als Abweichungen der Messwerte von ihrem Mittelwert bezeichnet.

Systematischer Fehler: Systematische Fehler sind Fehler die bei der Erhebung von Daten oder bei Durchführung von Datenanalysen entstehen und wiederholt auftreten. Sie verursachen eine Verzerrung der Messergebnisse und / oder zeichnen sich durch eine bestimmte Tendenz aus.

Interquartilsabstand (Interquartilbereich oder Quartilsabstand): Wird eine Stichprobe entsprechend ihrer Größe sortiert, so beschreibt der Interquartilsabstand (Quartilsabstand) die Breite des Intervalls, innerhalb dessen sich die mittlere Hälfte der Stichprobenelemente befindet. Hiermit wird der Bereich zwischen dem ersten und dem dritten Quartal bezeichnet.
 
Einstichprobentest - Einstichproben t-Test: Der Einstichprobentest (Einstichproben-t-Test) wird eingesetzt, um festzustellen, ob der Mittelwert einer Stichprobe mit Überzufälligkeit von einem vorgegebenen anderen (nicht der Probe zugehörigen) Wert abweicht.
 
Zweistichprobentest - Zweistichproben t-Test: Beim Zweistichprobentest  (Zwei-Stichproben-t-Test) wird eine Methode angewandt, mit Hilfe derer untersucht wird, ob die Mittelwerte zweier Stichproben identisch sind.

Student-t-Test - Einseitiger t-Test - Zweiseitiger t-Test: Der Student-t-Test (oder kurz t-Test) kann einseitig oder zweiseitig durchgeführt werden. Bei der Wahl des einseitigen t-Tests ist zu unterscheiden, ob dieser linksseitig oder rechtsseitig angewandt werden soll. Die Auswahl des anzuwendenden Verfahrens unterliegt der Richtung zugrundeliegender Hypothesen. Liegt eine gerichtete Hypothese vor, so ist vorzugsweise ein linksseitiger oder ein rechtsseitiger t-Test zu wählen (einseitiger Test). Handelt es sich um eine ungerichtete Hypothese, so wird der zweiseitige Test angewandt (zweiseitiger Test).

Z-Test - Gauß-Test: Beim Gauß-Test oder Z-Test handelt es sich um eine Gruppe von Hypothesentests mit einer Testprüfgröße die standardnormalverteilt ist. Der Gauß-Test folgt einer ähnlichen Methode wie der t-Test. Die Voraussetzungen für die Anwendung dieses Tests sind jedoch andere als bei einem t-Test, denn zur Duchführung eines derartigen Tests müssen die Standardabweichungen der Grundgesamtheiten bekannt sein.

Parameterschätzung: Eine Parameterschätzung (Schätzung) dient dazu, für nicht vorhandene Daten einer Verteilung (einer Stichprobe) einen Schätzwert zu erhalten und hierdurch Informationen über unbekannte Parameter wie den Erwartungswert oder die Varianz einer Grundgesamtheit zu erhalten. Eine derartige Schätzung wird auch als Schätzfunktion, Schätzer oder Schätzstatistik bezeichnet.

 

 

1. Test eines Stichprobenmittelwerts einer normalverteilten Grundgesamtheit:

 

Von der Stichprobe einer normalverteilten Grundgesamtheit sind bekannt:

 

Umfang der Stichprobe n

Varianz σ²

Mittelwert m

 

Es soll untersucht werden, ob der Mittelwert m vom zu erwartenden Mittelwert μ zufällig abweicht. Hierfür wird eine Nullhypothese H₀ aufgestellt, welche besagt, dass eine Abweichung des Mittelwerts m vom Erwartungswert m zufällig ist.

 

Zur Untersuchung der Gültigkeit der Nullhypothese wird eine Testgröße ta ermittelt, welche mit dem Wert einer Student-t-Verteilung tb verglichen wird. Ist ta < tb, so kann die Nullhypothese mit der entsprechend gewählten Irrtumswahrscheinlichkeit α beibehalten werden, ansonsten muss diese verworfen werden.

 

Diese Testgröße wird ermittelt durch:

 

 

mit f = n-1 Freiheitsgraden für Student-t-Wert

 

2. Test von zwei Stichprobenmittelwerten einer normalverteilten Grundgesamtheit:

 

Sind von zwei unabhängigen Stichproben einer normalverteilten Grundgesamtheit folgende Größen bekannt:

 

Umfang der 1. Stichprobe n1

Umfang der 2. Stichprobe n2

Mittelwert der 1. Stichprobe m1

Mittelwert der 2. Stichprobe m1

Varianz der 1. Stichprobe σ₁²

Varianz der 2. Stichprobe σ₂²

 

so kann diese Testgröße ermittelt werden durch:

 

 

mit f = n₁ + 2·n₂ Freiheitsgraden für Student-t-Wert

 

Die Untersuchung der Gültigkeit der Nullhypothese erfolgt wie zuvor beschrieben.
 

3. Test einer Stichprobenhäufigkeit:

 

Tritt in einer Stichprobe ein Ereignis der Häufigkeit h ein, und entspricht die zu erwartende Wahrscheinlichkeit des Eintretens p nicht dem empirisch ermittelten Wert h/n, so kann die Testgröße bzgl. der Nullhypothese eines zufälligen Abweichens ermittelt werden mit:

 

 

mit f = n-1 Freiheitsgraden für Student-t-Wert

 

und:

 

Stichprobenumfang n

Ereignishäufigkeit h

Erwartungswahrscheinlichkeit des Eintritts des Ereignisses p

 

Die Untersuchung der Gültigkeit der Nullhypothese erfolgt wie zuvor beschrieben.

 

 

Gehen Sie folgendermaßen vor, um Berechnungen in diesem Programmteil durchführen zu lassen:
 

1. Wählen Sie durch Aktivierung des entsprechenden Registerblatts, welche Untersuchung Sie durchführen möchten (Ein Stichprobenmittelwert, Zwei Stichprobenmittelwerte, Stichprobenhäufigkeit).
    

2. Geben Sie die Werte für benötigte Größen in die dafür zur Verfügung stehenden Felder ein.
    

3. Entscheiden Sie durch die Aktivierung der entsprechenden Kontrollschalter, ob ein- oder zweiseitige Tests durchgeführt werden sollen.
    

4. Legen Sie durch die Aktivierung des hierfür relevanten Kontrollschalters fest, für welche Irrtumswahrscheinlichkeiten ein Test durchgeführt werden soll.
    

5. Bedienen Sie hierauf die Schaltfläche Berechnen, so ermittelt das Programm, ob die Nullhypothese angenommen werden kann.

 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Stetige Verteilungen

Glockenkurve

 

 

Beispiel 1 - Stichprobenmittelwert einer normalverteilten Grundgesamtheit (Zweiseitiger Test):

 

Registerblatt Ein Stichprobenmittelwert.

 

Bei einer Stichprobe des Umfangs 65 werden die Werte für Varianz und Mittelwert wie folgt angegeben:

 

Varianz σ² = 1,6

Mittelwert m = 14,2

 

Der erwartete Mittelwert μ  beträgt 14. Nach Festlegung einer Irrtumswahrscheinlichkeit von α = 0,05 und der Eingabe der entsprechenden Werte (Umfang n = 65, Mittelwert m = 14,2, Varianz σ² = 1,6 und Erwartungswert μ = 14), ermittelt das Programm bei Durchführung eines zweiseitigen Tests:

 

Testwert ta: 1,275

Student-t-Wert tb: 1,998

 

Somit kann die Hypothese, dass die aufgetretene Abweichung zufällig eingetreten ist, angenommen werden.

 

Beispiel 2 - Stichprobenmittelwert einer normalverteilten Grundgesamtheit (Einseitiger Test):

 

Registerblatt Ein Stichprobenmittelwert.

 

Ein auf Erwartungswert μ = 50 und Varianz σ ² = 25 geeichter Raumvorstellungstest wird (Umfang) n = 100 Studentinnen und Studenten vorgegeben. Das durchschnittliche Testergebnis (Mittelwert) in der Stichprobe beträgt m = 50,9. Kann man aufgrund dieser Ergebnisse davon ausgehen, dass Studierende eine bessere räumliche Vorstellungskraft als die Gesamtbevölkerung aufweisen?

 

Nach Festlegung eines Signifikanzniveaus (Irrtumswahrscheinlichkeit) von α = 0,05, der Eingabe der Werte für Umfang n = 100, Mittelwert m = 50, Varianz σ² = 25 und Erwartungswert μ = 50, ermittelt das Programm bei Durchführung eines einseitigen Tests den Testwert ta = 1,8.

 

Da der kritische Wert für tb = 1,66 beträgt, und das Ergebnis somit signifikant ist (1,8 > 1,66), lautet die Antwort: Ja, man kann aufgrund der vorliegenden Stichprobe davon ausgehen, dass Studentinnen und Studenten im Durchschnitt eine bessere Raumvorstellung haben als die Gesamtbevölkerung.

 

Beispiel 3 - Zwei Stichprobenmittelwerte einer normalverteilten Grundgesamtheit:

 

Registerblatt Zwei Stichprobenmittelwerte.

 

Bei der Fertigung von Scheiben werden Proben von n1 = 75 und n2 = 50 Testexemplaren entnommen. Die Mittelwerte deren Höhen (in mm) betragen m1 = 40 bzw. m2 = 39,91. Die Varianzen weisen die Werte σ²₁ = 0,052 bzw. σ²₂ = 0,055 auf.

 

Die Nullhypothese besagt, dass diese Unterschiede auf Zufall beruhen. Bei Durchführung eines zweiseitigen Tests mit einer Irrtumswahrscheinlichkeit von α = 0,05 wird der Testwert ta = 2,137 ermittelt. Da der Student-t-Wert jedoch tb = 1,979 beträgt, kann gefolgert werden, dass die Differenz der Höhen signifikant ist und die Hypothese somit abgelehnt werden muss.

 

Beispiel 4 - Stichprobenhäufigkeit:

 

Registerblatt Zwei Stichprobenhäufigkeit.

 

Bei einer klinischen Studie wird ermittelt, dass nach Verabreichung eines Medikaments von 80 untersuchten Patienten 15 bestimmte Symptome aufweisen. Aus zuvor durchgeführten Langzeitstudien ist bekannt, dass die Erwartungswahrscheinlichkeit hierfür bei 0,3 liegt.

 

Bei Annahme einer Irrtumswahrscheinlichkeit von α = 0,01 (und Eingabe der Werte für Umfang n = 80, Häufigkeit h = 15 und Erwartungswahrscheinlichkeit p = 0,3), wird für den Testwert ta die Zahl 2,196 ermittelt. Da der entsprechende Wert der Student-t-Verteilung tb = 2,64 beträgt, wird bei Durchführung eines zweiseitigen Tests die Nullhypothese bestätigt und es kann davon ausgegangen werden, dass sich an der Häufigkeit des Erscheinens der Symptome nichts geändert hat.
 

 

Beispiel 1


Beispiel 2


Beispiel 3


Beispiel 4


Beispiel 5


Beispiel 6


Beispiel 7


Beispiel 8


Beispiel 9

     
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Stichprobe zu finden.

 

 

Kombinatorik - Urnenmodell - Pfadregel - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Regressionsanalyse - Stichproben - Verteilungen - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)

 

MathProf 5.0 - Unterprogramm Stichprobenauswertung

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---