MathProf - Kalendersystem - Osterdatum - Islamischer Kalender

 

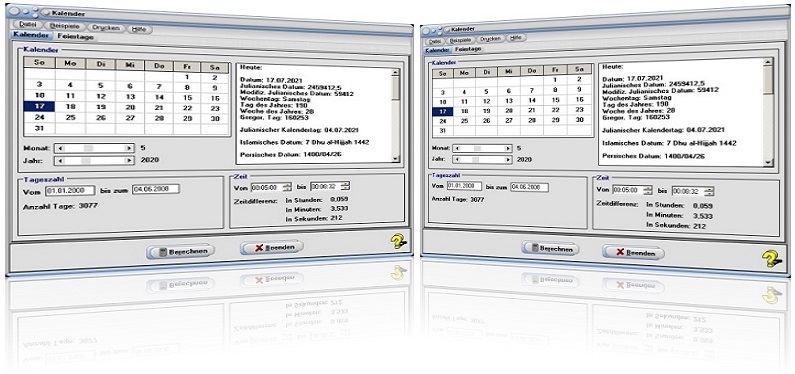
Modul Kalender

---

Das Unterprogramm [Sonstiges] - Kalender stellt eine kleine Hilfe dar, um Kalenderdaten ermitteln zu lassen.

 

 

 
Als Kalender wird eine Übersicht über die Tage, Wochen und Monate eines Jahres bezeichnet. Der Begriff Kalender entsammt dem lateinischen Wort Calendarium. Hierbei handelte es sich um ein Verzeichnis der jeweils ersten, auszurufenden Tage antiker Monate.

Das Datum (Kalenderdatum) ist die Benennung eines Tages binnen eines Kalenderjahres im Rahmen eines Kalenders. Beginn sowie Ende eines Tages hängen davon ab, auf welche Zeitzone sich die Angabe bezieht.

---

In diesem Modul wird Folgendes ermöglicht bzw. zur Verfügung gestellt:
 

• Ermittlung der Anzahl verstrichener Tage zwischen zwei Datumsangaben (Alter berechnen)
• Ermittlung von Zeitdifferenzen (innerhalb von 24h)
• Ausgabe von Datumsangaben in verschiedenen Kalendern:
  
  - Gregorianisches Datum
  - Julianisches Datum
  - Modifiziertes Julianisches Datum
  - Julianischer Kalendertag
  - Islamisches Datum
  - Persisches Datum
  - Bahâi'sches Datum
   
• Berechnung der Datumsangabe von Ostern, Pfingsten, Rosenmontag und Himmelfahrt

Es ermöglicht neben dem Umrechnen von Datumsangaben (Datum umrechnen) auch die Ermittlung von Zeitdifferenzen. Zudem lassen sich die Datumsangaben der Feiertage Ostern, Pfingsten, Rosenmontag und Himmelfahrt ausgeben.
 
 

 
Julianisches Datum: Beim Julianischen Datum handelt es sich um eine häufig in der Astronomie verwendete Tageszählung. Hierbei handelt es sich um eine fortlaufende Tageszählung, deren Beginn auf den 1. Januar 4713 vor Christus festgesetzt wurde und mit derer Hilfe Zeitdifferenzen auf einfache Weise berechnet werden können. In Form einer fortlaufenden Tageszählung ist das julianische Datum frei von Unregelmäßigkeiten wie unterschiedlich langen Monaten und Schalttagen usw., wie sie bei den meisten Kalendern auftreten.

Modifiziertes Julianisches Datum: Das modifizierte Julianische Datum (MJD) ist eine von der amerikanischen Smithsonian Institution eingeführte Zeitskala für die Chronologie sowie für Geowissenschaften. Als Nullpunkt dieser Zeitskala ist der 17. November 1858 festgelegt.

Julianischer Kalender: Der julianische Kalender ist einer der ältesten Solarkalender und ist Vorläufer des heute häufig benutzten gregorianischen Kalenders. Er wurde im Jahr 45 v. Chr. von Julius Caesar im Römischen Reich eingeführt. Im Jahr 1582 wurde er schrittweise durch den verbesserten gregorianischen Kalender abgelöst. Dieser Kalender setzt sich aus 365-tägigen Gemeinjahren, die in 12 Monate unterschiedlicher Länge eingeteilt sind, zusammen. Er weist eine Zeitdifferenz von 13 Tagen hinsichtlich des gregorianischen Kalenders auf. Jedes vierte Jahr im Julianischen Kalender war ein Schaltjahr. Dies hatte zur Folge, dass ein julianisches Jahr durchschnittlich 365,25 Tage dauerte und somit bezüglich eines Sonnenjahrs zu lang war.

Islamischer Kalender: In islamischen Staaten richten Einwohner ihr religiöses Leben nach dem Mondkalender aus, dem islamischen Kalender. Die Hidschra ist das Jahr, auf die Muslime das Jahr 0 festlegten. Dies erfolgte nach christlichen Zeitrechnung im Jahr 622 n. Chr. Insgesamt umfasst dieser Kalender lediglich 354 Tage. Dies beruht auf der Tatsache, dass er 10 oder 11 Tage kürzer ist als der Grogorianische Kalender, da seine Monate entweder lediglich 29 oder 30 Tage lang sind. Er richtet sich entgegen dem Gregorianischen Kalender nicht nach der Sonne und ist somit kein Sonnenkalender.

Persischer Kalender: Anders als der gregorianische Kalender stützt sich der persische Kalender auf astronomische Beobachtungen. Er ist ein Sonnenkalender. Das Jahr 1 des persischen Kalenders entspricht dem Jahr 622 n. Chr. des gregorianischen Kalenders. Seine Zeitrechnung beruht auf dem Sonnenjahr, dessen Länge durch die Bewegung der Erde um die Sonne bestimmt wird. Er wird auch als iranischer Kalender bezeichnet, ist der offizielle Kalender in Afghanistan und Iran und gilt als einer der präzisesten seiner Art.

Gregorianischer Kalender: Der gregorianische Kalender ist der weltweit am häufigsten eingesetze Kalender. Er wurde durch eine Reform des julianischen Kalenders im Jahr 1582 ins Leben gerufen. Benannt wurde er nach Papst Gregor XIII, der ihn im Februar dieses Jahres einführte. Er wird auch als Christlicher Kalender bezeichnet. Beim gregorianischen Kalender handelt es sich um einen Sonnenkalender. Dieser bezieht sich (im Gegensatz zu Mondkalendern) auf den Lauf der Erde um die Sonne. Die meisten seiner zwölf Monate besitzen eine Dauer von 30 bzw. 31 Tagen. Der Monat Februar weist in einem Gemeinjahr eine Länge von 28 Tagen auf. Alle vier Jahre (in jedem Schaltjahr) wird ihm ein zusätzlicher Tag hinzugefügt und er besitzt in solch einem Jahr somit eine Länge von 29 Tagen.

Kalenderjahr: Unter dem Begriff Kalenderjahr wird die zwischen dem 1. Januar bis zum 31. Dezember eines Jahres verstreichende Zeit verstanden.

Kalendersystem: Kalendersysteme ermöglichen einen Überblick über die Tage, Wochen und Monate eines Jahres. Es existieren verschiedene derartige Systeme, heute ist jedoch weltweit überwiegend der gregorianische Kalender in Gebrauch.

Kalendertage: Ein Kalendertag ist ein im Kalender spezifizierbarer Tag bzw. ein exakt definierbares (angebbares) Datum.

Osterdatum: Als Osterdatum wird das Datum des Osterfests im Kirchenjahr genannt. Es ist der erste Sonntag nach dem ersten Vollmond im Frühling eines Jahres. Fällt der Frühlingsvollmond auf einen Sonntag, so wird Ostern am darauf folgenden Sonntag gefeiert.

Alter berechnen (Altersberechnung): Mit dem in diesem Modul implementierten Altersrechner wird es ermöglicht, sich das Alter (das Lebensalter) in Tagen berechnen und ausgeben zu lassen.

Kalenderberechnung (Kalenderrechnung): Unter dem Begriff Kalenderrechnung wird das Berechnen eines Kalenders bezeichnet, welches innerhalb eines bestimmten Kalendersystems durchgeführt wird. Berechnungen dieser Art sind notwendig, um damit ein Kalendarium erstellen zu können. Ein Kalenderrechner ist ein Rechner mit Hilfe dessen die Kalenderberechnung durchgeführt wird.
 
Kalendermonate: Bei einem Kalendermonat handelt es sich um einen Monat, wie er im Kalender steht. Er beginnt mit dem Anfang des Monats und endet mit dem letzten Tag des Monats (z.B. vom 01.04. - 30.04.). Er beginnt, unabhängig vom ersten Arbeitstag, stets am ersten Tag eines Monats (z.B. am 01.07 oder 01.11).

Datumsrechner: Ein Datumsrechner berechnet anhand eines vorgegebenen Anfangsdatums sowie eines definierten Enddatums die Anzahl der binnen dieses festgelegten Zeitraums verstrichenen Tage.

Datumsberechnung: Eine Datumsberechnungen dienen dazu, die Anzahl der zwischen zwei Datumsangaben verstrichenen Tage zu ermitteln.

Datumsdifferenz: Als Datumsdifferenz wird der zwischen zwei Datumswerten existierende Abstand in Tagen, Monaten oder Jahren bezeichnet.

Jahreszahlen: Eine Jahreszahl ist eine Zahl, mit der ein Jahr der Zeitrechnung entsprechend beschrieben wird. Bsp.: 2021 - Diese Jahreszahl bedeutet das Jahr 2021 nach Christi Geburt.

Wochentage: Als Wochentag wird ein Tag der Woche bezeichnet, der in gleichbleibender Reihenfolge und wiederkehrender Bezeichnung über das gesamte Jahr des bürgerlichen Kalenders hinweg vorkommt. Wochentage tragen im deutschen Sprachraum die Bezeichnungen Montag, Dienstag, Mittwoch, Donnerstag, Freitag, Samstag (oder Sonnabend) und Sonntag.

Jahreszahl: Jahreszahlen sind Zahlen mit denen einzelne Jahre der Zeitrechnung entsprechend angegeben werden.

Jahrzehnte: Als Jahrzehnt oder Dekade wird ein Zeitraum bezeichnet, der zehn Jahre dauert.
Jahrhunderte: Ein Jahrhundert wird der Zeitraum genannt, der einhundert Jahre (oder zehn Jahrzehnte) dauert.
Jahrtausende: Als Jahrtausend wird ein Zeitraum bezeichnet, der eintausend Jahre (oder zehn Jahrhunderte) dauert.

Kalenderwoche: Als Kalenderwochen werden Wochen benannt, die mit dem Montag beginnen und mit dem Sonntag enden. Das Jahr umfasst insgesamt mindestens 52 Kalenderwochen, kann jedoch auch über 53 Kalenderwochen verfügen. Die Anzahl der Kalenderwochen eines Jahres ist abhängig davon, mit welchem Wochentag das Jahr beginnt und ob es sich um ein gemeines Jahr oder ein Schaltjahr handelt.

Tagesnummern: Mit dem Begriff Tagesnummer wird der Tag des Jahres der diesem Datum entspricht, bezeichnet. Auch diese wird von diesem Programm ermittelt und mit der Bezeichnung Tag des Jahres ausgegeben.

 

 
Um sich die Feiertage innerhalb des Zeitraums von 1 - 3000 n. Chr. ausgeben zu lassen, wählen Sie das Registerblatt Feiertage, geben die Jahreszahlen für den Zeitbereich über den Sie sich die Feiertage ausgeben lassen möchten, in die dafür zur Verfügung stehenden Felder ein und bedienen die Schaltfläche Berechnen.

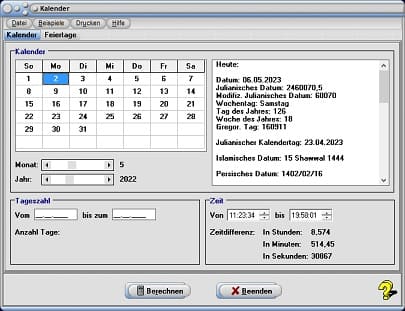
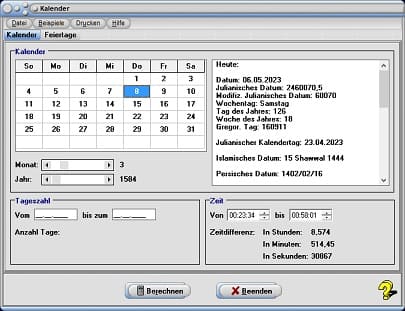
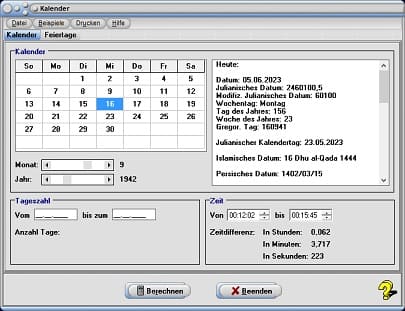
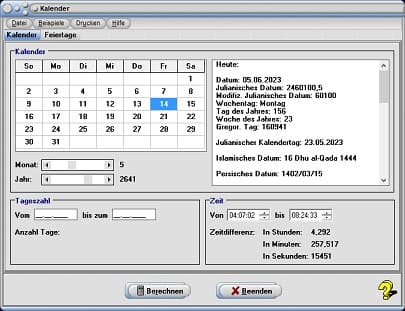
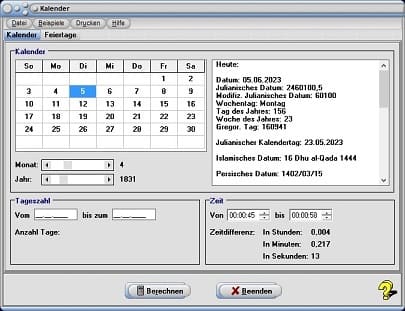
Um Kalenderdaten innerhalb des Zeitraums von 1583 - 3000 n. Chr. abzufragen, wählen Sie das Registerblatt Kalender. Durch die Positionierung des Rollbalkens Monat legen Sie den Kalendermonat und durch eine Bedienung des Rollbalkens Jahr die Jahreszahl fest, für welche Kalenderdaten ausgegeben werden sollen. Den Tag bestimmen Sie durch einen Mausklick auf das entsprechende Feld im Monatskalender. Daraufhin gibt das Programm die entsprechenden Daten für das im Kalender selektierte, wie auch für das aktuelle Datum in der rechtsseitig angeordneten Tabelle aus.

Zudem ermittelt es die Anzahl verstrichener Tage vom gewählten Kalenderdatum bis zum aktuellen Datum. Um die Anzahl verstrichener Tage zwischen zwei Datumsangaben (bzw. ein Alter oder Lebensalter in Tagen) ermitteln zu lassen, geben Sie diese in die Felder im Formularbereich Tagesanzahl ein und bedienen hierauf die Schaltfläche Berechnen.

Die Ermittlung einer Zeitdifferenz (innerhalb von 24h) lassen Sie durchführen, indem Sie die entsprechenden Uhrzeiten im Formularbereich Zeit festlegen und danach die Schaltfläche Berechnen bedienen.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Benutzbarbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens genutzt werden.
 
Oftmals lassen sich hiermit auch die Lösungen von Mathe-Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf anschauliche Weise untersucht werden. Dieses Modul kann auch dabei hilfreich sein, einen Begriff zum entsprechenden Fachthema zu erklären. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthemengebiet.
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
 

 

Beispiel Kalender:

Wählen Sie das Registerbaltt Kalender. Nach einer Festlegung des Datums 17.09.1723 durch Positionierung der entsprechenden Rollbalken und einem Klick auf die Tageszahl 17 im Kalender, gibt das Programm für diesen gewählten Kalendertag aus:

 

Datum: 17.09.1723

Julianisches Datum: 2350361,5

Modifiziertes Julianisches Datum: -49369

Wochentag: Freitag

Tag des Jahres: 260

Woche des Jahres: 37

Gregorianischer Tag: 51472

Julianischer Kalendertag: 06.09.1723

Islamisches Datum: 16 Dhu al-Hijjah 1135

Persisches Datum: 1102/06/26
 

Für das Bahâi'sche Datum gibt das Programm nichts aus,

da dieser Kalender erst seit dem Jahr 1853 in Benutzung ist.
 

Beispiel Datum:

Wählen Sie das Registerbaltt Kalender. Nach Eingabe der Datumswerte 05.03.1788 und 14.2.2001 in die dafür vorgesehenen Felder im Formularbereich Tageszahl erhalten Sie für die Anzahl verstrichener Tage zwischen den beiden Datumsangaben nach einer Bedienung der Schaltfläche Berechnen den Wert 77777.

Beispiel Zeit:

Wählen Sie das Registerbaltt Kalender. Wurden die Uhrzeiten 2:00:00 h und 14:30:00 h in die Felder im Formularbereich Zeit eingegeben, so werden Ihnen, nach einer Bedienung der Schaltfläche Berechnen, folgende Werte für die Zeitdifferenz der beiden Uhrzeiten ausgegeben:

In Stunden: 12,5 h

In Minuten: 750 min

In Sekunden: 45000s
 

Beispiel Feiertage:

Wählen Sie das Registerbaltt Feiertage. Nach einer Festlegung der Jahreszahlen 1788 und 1788 in den zur Verfügung stehenden Felder, gibt das Programm nach einem Klick auf die Schaltfläche Berechnen für das Jahr 1788 aus:

 

Ostern 1788: 23.03.1788

Pfingsten 1788: 11.05.1788

Rosenmontag 1788: 04.02.1788

Himmelfahrt 1788: 01.05.1788
 

 

Beispiel 1


Beispiel 2


Beispiel 3


Beispiel 4


Beispiel 5


Beispiel 6


Beispiel 7


Beispiel 8

      

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Kalender, Wikipedia - Julianischer Kalender, Wikipedia - Islamischer Kalender sowie unter Wikipedia - Gregorianischer Kalender zu finden.

 

 

Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach

 

MathProf 5.0 - Unterprogramm Raumgittermodelle

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---