MathProf - Statistik - Zufallsstichprobe - Stichproben - Verfahren

 

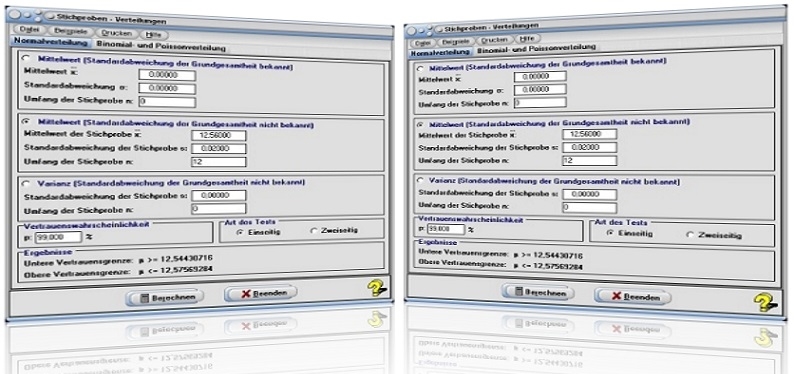
Modul Stichproben - Verteilungen

---

 
Im Unterprogramm [Stochastik] - [Stichproben] - Verteilungen können Untersuchungen mit Stichproben bzgl. derer Konfidenzintervalle durchgeführt werden.

 

Die mathematischen Grundlagen zur Untersuchung statistischer Verfahren liefert die Wahrscheinlichkeitstheorie sowie die Wahrscheinlichkeitsrechnung. Sie ist ist ein Teilgebiet der Mathematik, welches sich mit der Modellierung sowie der Analyse von Zufallsereignissen beschäftigt. Unter dem Begriff Statistik wird die Lehre von Methoden zum Umgang mit Daten verstanden. Die schließende Statistik ermöglicht es, von den Werten einer kleinen Stichprobe auf die Grundgesamtheit zu schließen.
 
Dieses Modul ermöglicht die Ermittlung von Vertrauensgrenzen bzw. Vertrauensbereichen beim Vorliegen von Daten aus Stichproben, wenn Sachverhalte folgender Art gegeben sind:
 

• Normalverteilung - Mittelwert (Standardabweichung der Grundgesamtheit bekannt)

• Normalverteilung - Mittelwert (Standardabweichung der Grundgesamtheit nicht bekannt)

• Normalverteilung - Varianz (Standardabweichung der Grundgesamtheit nicht bekannt)

• Binomialverteilung

• Poissonverteilung
   

Als Sicherheitswahrscheinlichkeit oder Vertrauenswahrscheinlichkeit (1-α) wird die Gegenwahrscheinlichkeit der Irrtumswahrscheinlichkeit α bezeichnet. Sie besitzt in vielen Fällen Werte von 0,9, 0,95, 0,975 oder 0,99, bzw. 90%, 95%, 97,5% oder 99%.
 

 

Mittelwert (Standardabweichung der Grundgesamtheit bekannt):

 

Ist die Standardabweichung von Daten bekannt, so können die Vertrauensgrenzen (Perzentile bzw. Quantile) für den Mittelwert μ (dieser trägt auf dem Formular die Bezeichnung x) zur Vertrauenswahrscheinlichkeit 1-α folgendermaßen errechnet werden:

 

Einseitige untere Vertrauensgrenze:

 

 

Einseitige obere Vertrauensgrenze:

 

 

Zweiseitiger Vertrauensbereich:

 

 

Um Analysen dieser Art durchführen zu können, werden Angaben zu Mittelwert, Standardabweichung sowie dem Umfang der Grundgesamtheit benötigt.

 

Mittelwert (Standardabweichung der Grundgesamtheit nicht bekannt):

 

Ist die Standardabweichung von Daten nicht bekannt, so lassen sich die Vertrauensgrenzen für den Mittelwert μ (dieser trägt auf dem Formular die Bezeichnung x) zur Vertrauenswahrscheinlichkeit 1-α durch folgende Zusammenhänge bestimmen:

 

Einseitige untere Vertrauensgrenze:

 

 

Einseitige obere Vertrauensgrenze:

 

 

Zweiseitiger Vertrauensbereich:

 

 

Um Analysen dieser Art durchführen zu können, werden Angaben zu Mittelwert, Standardabweichung und Umfang der Stichprobe benötigt.

 

Varianz (Standardabweichung der Grundgesamtheit nicht bekannt):

 

Ist die Standardabweichung s von Daten nicht bekannt, so können, analog zum Mittelwert, auch die Vertrauensgrenzen für die Varianz zur Vertrauenswahrscheinlichkeit 1-α folgendermaßen bestimmt werden:

 

Einseitige untere Vertrauensgrenze:

 

 

Einseitige obere Vertrauensgrenze:

 

 

Zweiseitiger Vertrauensbereich:

 

 

Um Analysen dieser Art durchführen zu können, werden Angaben zu Standardabweichung und Umfang der Stichprobe benötigt.

 

 

Liegt eine Binomialverteilung vor, so können die Vertrauensgrenzen p zur Vertrauenswahrscheinlichkeit 1-α wie nachfolgend aufgeführt errechnet werden:

 

Einseitige untere Vertrauensgrenze:

 

 

Einseitige obere Vertrauensgrenze:

 

 

Zweiseitiger Vertrauensbereich:

 

 

mit:

 

 

 

Um Analysen dieser Art durchführen zu können, werden Angaben zu Losgröße und Umfang der Stichprobe benötigt.

 

 

Liegt eine Poissonverteilung vor, so lassen sich die Vertrauensgrenzen p zur Vertrauenswahrscheinlichkeit 1-α wie folgt ermitteln:

 

Einseitige untere Vertrauensgrenze:

 

 

Einseitige obere Vertrauensgrenze:

 

 

Zweiseitiger Vertrauensbereich:

 

 

mit:

 

 

 

Um Analysen dieser Art durchführen zu können, werden Angaben zum Umfang der Stichprobe benötigt.

 

 

Gehen Sie folgendermaßen vor, um die Vertrauensgrenzen bzw. Vertrauensbereiche beim Vorliegen von Stichprobenergebnissen o.a. Fälle ermitteln zu lassen.
 

1. Selektieren Sie das Registerblatt Normalverteilung bzw. Binomial- und Poissonverteilung und aktivieren Sie den entsprechenden Kontrollschalter.
    

2. Geben Sie die benötigten Daten in die dafür vorgesehenen Felder ein.
    

3. Legen Sie durch die Eingabe eines relevanten Zahlenwerts (zwischen 0,001 und 99,999) in das Feld Vertrauenswahrscheinlichkeit den Wert für die Vertrauenswahrscheinlichkeit α fest (in %).
    

4. Wählen Sie durch die Aktivierung des Kontrollschalters Einseitig bzw. Zweiseitig die Art des durchzuführenden Tests.
    

5. Nach einer Bedienung der Schaltfläche Berechnen ermittelt das Programm die entsprechenden Vertrauensgrenzen (Vertrauensbereiche) und gibt diese aus.

 

Möchten Sie derartige Untersuchungen mit konkret vorliegenden (normalverteilten) Messdaten durchführen, so verwenden Sie das Unterprogramm Statistische Messwertanalyse um Mittelwerte und Standardabweichungen bestimmen zu lassen und benutzen anschließend dieses Modul um Vertrauensgrenzen bzw. Vertrauensbereiche berechnen zu lassen.

 

Die in diesem Modul zur Ermittlung von Ergebnissen verwendeten (benötigten) Werte der Quantile für Irrtums- bzw. Vertrauenswahrscheinlichkeiten der Student-t-, Chi²-, normierten Gauß- und der F-Verteilung stehen im Unterprogramm Stetige Verteilungen in tabellarischer Form zur Verfügung.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf einfache Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthema.

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Stichproben

Stetige Verteilungen

Binomialverteilung

Poisson-Verteilung

Statistische Messwertanalyse

 

 

Beispiel 1 - Mittelwert (Standardabweichung der Grundgesamtheit bekannt):

 

Es sei bekannt, dass 7 Messwerte aus einer Normalverteilung mit Standardabweichung der Grundgesamtheit 0,01 stammen. Der Mittelwert der sieben Messungen beträgt 10,2109.

 

Was ist die obere und untere Vertrauensgrenze für den Mittelwert zur Vertrauenswahrscheinlichkeit 99%?

 

Vorgehensweise und Lösung:

 

Nach einer Aktivierung des Kontrollschalters Mittelwert (Standardabweichung der Grundgesamtheit bekannt) auf dem Registerblatt Normalverteilung, der Eingabe der Werte 10.2109, 0.01 und 7 in die Felder Mittelwert, Standardabweichung und Umfang der Stichprobe, sowie der Festlegung des Werts 99 im Feld Vertrauenswahrscheinlichkeit und der Aktivierung des Kontrollschalters Einseitig, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen:

 

Untere Vertrauensgrenze: μ ≥ 10,210207

Obere Vertrauensgrenze: μ   ≥ 10,227793

 

Aktivieren Sie den Kontrollschalter Zweiseitig, und belassen Sie alle anderen Einstellungen auf den soeben festgelegten, so ermittelt das Programm:

 

Zweiseitiger Vertrauensbereich: 10,209264 ≤ μ ≤ 10,228735

 

Beispiel 2 - Mittelwert (Standardabweichung der Grundgesamtheit nicht bekannt):

 

Es sei bekannt, dass 7 Messwerte aus einer Normalverteilung stammen und die Standardabweichung der Grundgesamtheit nicht bekannt ist. Der Mittelwert der sieben Messungen beträgt 10,2109. Die Standardabweichung der Messwerte beträgt 0,01087.

 

Was ist die obere und untere Vertrauensgrenze für den Mittelwert zur Vertrauenswahrscheinlichkeit 95%?

 

Vorgehensweise und Lösung:

 

Nach einer Aktivierung des Kontrollschalters Mittelwert (Standardabweichung der Grundgesamtheit nicht bekannt) auf Registerblatt Normalverteilung, der Eingabe der Werte 10,2109, 0.01 und 7 in die Felder Mittelwert der Stichprobe, Standardabweichung der Stichprobe und Umfang der Stichprobe, sowie der Festlegung des Werts 95 im Feld Vertrauenswahrscheinlichkeit und der Aktivierung des Kontrollschalters Einseitig, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen:

 

Untere Vertrauensgrenze: μ ≥; 10,20355

Obere Vertrauensgrenze: μ ≤ 10,21824

 

Aktivieren Sie den Kontrollschalter Zweiseitig, und belassen Sie alle anderen Einstellungen auf den soeben festgelegten, so gibt das Programm aus:

 

Zweiseitiger Vertrauensbereich: 10,20165 ≤ μ ≤ 10,22015

 

Beispiel 3 - Varianz (Standardabweichung der Grundgesamtheit nicht bekannt):

 

Es sei bekannt, dass 7 Messwerte aus einer Normalverteilung stammen. Die Standardabweichung der Messwerte beträgt 0,01087.

 

Was ist die obere und untere Vertrauensgrenze für die Varianz (bzw. Standardabweichung) zur Vertrauenswahrscheinlichkeit 99%?

 

Vorgehensweise und Lösung:

 

Nach einer Aktivierung des Kontrollschalters Varianz (Standardabweichung der Grundgesamtheit nicht bekannt) auf Registerblatt Normalverteilung, der Eingabe der Werte 0,01087 und 7 in die Felder Standardabweichung der Stichprobe und Umfang der Stichprobe, sowie der Festlegung des Werts 99 im Feld Vertrauenswahrscheinlichkeit und der Aktivierung des Kontrollschalters Einseitig, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen:

 

Untere Vertrauensgrenze: σ² ≥; 0,00004217

Obere Vertrauensgrenze: σ² ≤ 0,00081292

 

Aktivieren Sie den Kontrollschalter Zweiseitig, und belassen Sie alle anderen Einstellungen auf den soeben festgelegten, so ermittelt das Programm:

 

Zweiseitiger Vertrauensbereich 0,00003822 ≤ σ² ≤ 0,001049

 

Beispiel 4 - Binomialverteilung:

 

Bei der Untersuchung einer Stichprobe von n = 100 Stück werden m = 3 schlechte Teile gefunden. Was ist die obere Vertrauensgrenze für den Anteil schlechter Teile p zur Vertrauenswahrscheinlichkeit 95%?

 

Vorgehensweise und Lösung:

 

Nach einer Aktivierung des Kontrollschalters Binomialverteilung auf dem Registerblatt Binomial- und Poissonverteilung, der Eingabe der Werte 3 und 100 in die Felder Losgröße und Umfang der Stchprobe, sowie der Festlegung des Werts 99 im Feld Vertrauenswahrscheinlichkeit und der Aktivierung des Kontrollschalters Einseitig, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen:

 

Untere Vertrauensgrenze: p ≥; 0,00439 = 0,439 %

Obere Vertrauensgrenze: p ≤ 0,0969 = 9,69 %

 

Aktivieren Sie den Kontrollschalter Zweiseitig, und belassen Sie alle anderen Einstellungen auf den soeben festgelegten, so gibt das Programm aus:

 

Zweiseitiger Vertrauensbereich: 0,003407 ≤ p ≤ 0,10548 bzw. 0,3407 % ≤ p ≤ 10,548 %

 

Beispiel 5 - Poissonverteilung:

 

Bei der Untersuchung einer Rolle mit Isolierdraht wurde n = 3 Fehler gefunden. Was ist die obere Vertrauensgrenze für die mittlere Anzahl der Fehler zur Vertrauenswahrscheinlichkeit 95%?

 

Vorgehensweise und Lösung:

 

Nach einer Aktivierung des Kontrollschalters Poissonverteilung auf Registerblatt Binomial- und Poissonverteilung, der Eingabe des Werts 3 in das Feld Umfang der Stichprobe, sowie der Eingabe des Werts 95 in das Feld Vertrauenswahrscheinlichkeit und der Aktivierung des Kontrollschalters Einseitig, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen:

 

Untere Vertrauensgrenze: μ ≥ 0,81769

Obere Vertrauensgrenze: μ ≤ 7,75365

 

Aktivieren Sie den Kontrollschalter Zweiseitig, und belassen Sie alle anderen Einstellungen auf den soeben festgelegten, so gibt das Programm für den zweiseitigen Vertrauensbereich aus: 0,61867 ≤ μ ≤ 8,76727.
 

 

Beispiel 1


Beispiel 2


Beispiel 3

  

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Stichprobe zu finden.

 

Kombinatorik - Urnenmodell - Pfadregel - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Regressionsanalyse - Stichproben - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)

 

MathProf 5.0 - Unterprogramm Stichproben

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---