MathProf - Rechteck - Quadrat - Raute - Drachenviereck - Trapez - Rechner

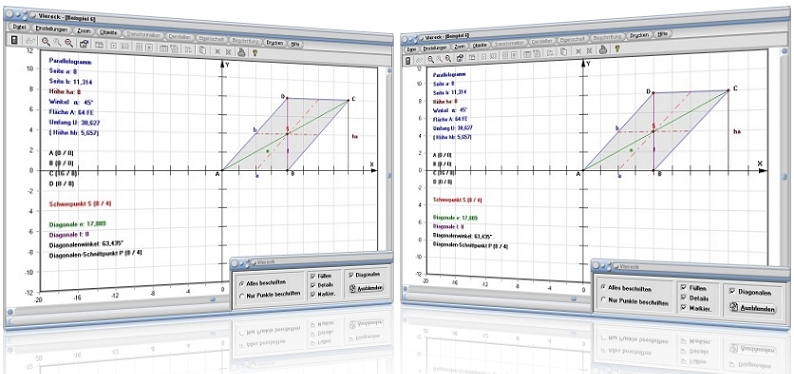
Modul Viereck

---

 
Das Unterprogramm [Geometrie] - [Viereck] - Viereck ermöglicht die numerische Bestimmung von Viereckgrößen (u.a. die Flächenberechnung), sowie die grafische Darstellung berechneter Vierecke.

 
 
Es stehen in diesem Modul folgende Arten von Vierecken (Viereckstypen) zur Verfügung, mit welchen Berechnungen durchgeführt werden können:
 

• Rechteck (Quadrat)

• Parallelogramm und Raute (Rhombus)

• Trapez

• Drachenviereck

   
Ein Rechteck besteht aus zwei je zwei gleich langen Seiten. Alle seine Seiten stehen rechtwinklig zueinander. Seine Diagonalen sind gleich lang und halbieren sich gegenseitig.

Ein Quadrat besteht aus vier gleich langen Seiten. Sie stehen rechtwinklig zueinander. Seine Diagonalen halbieren sich und stehen senkrecht aufeinander. Als Einheitsquadrat wird ein Quadrat bezeichnet, dessen Seitenlängen den Wert eins besitzen.
 
Ein Trapez ist konvexes Viereck, welches mindestens ein Paar paralleler Seiten besitzt. Seine Mittellinie m verläuft parallel zu den Grundlinien a und c und ist halb so lang, wie seine Grundlinien zusammen.

Schiefwinkliges Trapez: Im schiefwinkligen Trapez sind zwei einander gegenüberliegende Seiten parallel, die beiden anderen Seiten sind gleich lang. Es besitzt zwei Paare benachbarter Winkel von gleicher Größe.

Rechtwinkliges Trapez: Ein Trapez heißt rechtwinklig, wenn es über zwei rechte Innenwinkel (zwei rechte Winkel) verfügt. Ein symmetrisches Trapez, oder gleichschenkliges Trapez ist achsensymmetrisch. Seine Winkel an den parallel liegenden Seiten sind gleich groß und seine Schenkel verlaufen parallel zueinander.

Allgemeines Trapez: Als allgemeines Trapez wird ein Trapez bezeichnet, welches vier unterschiedlich lange Seiten besitzt von denen zwei parallel verlaufen.
 
Ein Drachenviereck (Deltoid) besitzt zwei Diagonalen, welche senkrecht aufeinander stehen. Eine seiner Diagonalen ist Symmetrieachse. Sie zerlegt es in zwei kongruente Dreiecke. Von der anderen Diagonale wird es in zwei gleichschenklige Dreiecke zerlegt.

Bei einem Parallelogramm sind gegenüberliegende Seiten sowie gegenüberliegende Winkel gleich groß. Benachbarte Winkel ergänzen sich zu 180°. Seine Diagonalen halbieren sich. Der Schwerpunkt eines Parallelogramms ist der Schnittpunkt seiner Diagonalen.

Eine Raute (Rhombus) ist ein ebenes Viereck, welches vier gleich lange Seiten besitzt. Gegenüberliegende Seiten sind parallel und gegenüberliegende Winkel gleich groß. Die Raute ist ein Sonderfall des Parallelogramms, die auch Rhombus genannt wird.
   
Themenrelevante Fachbegriffe:

Diagonalen: Als Diagonale wird eine Strecke bezeichnet, die Ecken von Flächen (oder Körpern) miteinander verbindet, ohne selbst eine Seite bzw. Kante der Figur zu sein.

Beschriftung: Die Beschriftung eines Rechtecks, eines Quadrats, eines Parallelogramms, einer Raute oder eines Trapezes erfolgt entgegen dem Uhrzeigersinn mit den Buchstaben A, B, C und D.

Zerlegungsgleichheit (Flächengleichheit): Zwei Figuren werden als zerlegungsgleich oder flächengleich bezeichnet, wenn sie sich in paarweise kongruente Teilpolygone zerlegen lassen. Zerlegungsgleich sind das Parallelogramm und das Rechteck. Zerlegungsgleiche Figuren besitzen den gleichen Flächeninhalt.

Planimetrie: Unter dem Begriff Planimetrie werden Problemstellungen der ebenen Geometrie, hauptsächlich die Berechnung von Flächeninhalten in der Ebene verstanden.

Winkelsymmetrale: Als Winkelsymmetrale wird die Symmetrieachse eines Winkels bezeichnet. Sie halbiert diesen und verläuft durch dessen Scheitel.

Mittelparallele: Als Mittelparallele wird die Verbindungsstrecke der Mittelpunkte der beiden nicht parallel verlaufenden Seiten eines Trapezes bezeichnet. Sie verläuft parallel zu den parallel liegenden Seiten des Trapezes.

Fläche: Die Fläche (der Flächeninhalt) beschreibt das Maß einer ebenen und begrenzten Figur.

Flächenmittelpunkt: Als Flächenmittelpunkt wird der geometrische Schwerpunkt einer Fläche bezeichnet.

Seitenlänge: Als Seitenlängen werden die Abstände eines Polygons bezeichnet, den die jeweiligen zwei Ecken voneinander besitzen.

Symmetrieachsen: Eine Symmetrieachse (Spiegelachse) ist eine Gerade durch welche eine Figur in zwei identische Teile geteilt wird.

Achsensymmetrie: Eine Figur wird als achsensymmetrisch bezeichnet, wenn sie durch die vertikale Achsenspiegelung an ihrer Symmetrieachse auf sich selbst abgebildet wird.

Besondere Vierecke: Als besondere Vierecke werden das Rechteck, das Quadrat, das Parallelogramm, die Raute und das Trapez bezeichnet.

Schwerpunkt (Flächenschwerpunkt oder geometrischer Schwerpunkt): Der Schwerpunkt einer geometrischen Figur ist ein spezieller Punkt, welcher als geometrischer Mittelpunkt interpretiert wird. Bei Linien wird er als Linienschwerpunkt, bei Flächen als Flächenschwerpunkt und bei Körpern als Volumenschwerpunkt bezeichnet.
 
Winkelsumme im Viereck: Jedes Viereck besitzt eine Winkelsumme (Innenwinkelsumme) von 360°.

Seitenmitten: Als Seitenmitte wird in diesem Zusammenhang der Mittelpunkt der Seite eines Vierecks bezeichnet.

Flächenformen: Als Flächenformen werden Flächen bezeichnet, die unterschiedliche Formen besitzen können. Zu diesen zählen in der Geometrie unter anderem der Kreis, das Rechteck, das Quadrat, das Parallelogramm, die Raute und das Trapez.
 
 

 
Nachfolgend aufgeführt sind einige Formeln, welche zur Berechnung der Werte entsprechender Größen eines Rechtecks, eines Quadrats, eines Parallelogramms, eines Trapezes oder Drachenvierecks relevant sind.

Rechteck:

Flächeninhalt: A = a·b
Umfang: U = 2·(a + b)
Diagonalenlänge: d = √a² + b²
Umkreisradius: r_u = 1/2·√a² + b²

Mit:
a,b: Seiten des Rechtecks

Quadrat:

Flächeninhalt: A = a²
Umfang: U = 4·a
Diagonalenlänge: d = a·√2
Inkreisradius: r_i = a/2
Umkreisradius: r_u = a/√2
Winkelsumme: α + β + γ + δ = 360°

Mit:
a: Seitenlänge des Quadrats
 
Parallelogramm (Raute):

Höhe auf Seite a: h_a = b·sin(α)
Höhe auf Seite b: h_b = a·sin(α)
Diagonale: e = √a² + b² - 2ab·cos (β)
Diagonale: f = √a² + b² - 2ab·cos (α)
Umfang: U = 2·(a + b)
Flächeninhalt: A = a·b·sin(α) = a·b·sin(β) = a·h_a = b·h_b

Mit:
a: Lange Grundseite
b,d: Schenkel
c: Kurze Grundseite
α,β: Untere Innenwinkel des Parallelogramms

Trapez:

Höhe: h = b·sin(β) = b·sin(γ) = d·sin(α) = d·sin(δ) 
Seite: a = c + l₁ + l₂
mit den seitlichen Überständen l₁ = √d² - h² und l₂ = √b² - h²
Inneninkel: α = arccos( (l₁²+d²-h²) / (2·l₁·d) )
Inneninkel: β = arccos( (l₂²+b²-h²) / (2·l₂·b) )
Innenwinkel: α + δ = 180°
Innenwinkel: β + γ = 180°
Diagonale: e = √a² + b² - 2ab·cos(β)
Diagonale: f = √a² + d² - 2ad·cos(α)
Mittellinie: m = (a + c) / 2
Umfang: U = a + b + c + d
Flächeninhalt: A = (a + c) / 2·h

Mit:
a,b,c,d: Seiten des Parallelogramms
α,β,γ,δ: Innenwinkel des Parallelogramms

 
Drachenviereck (Deltoid):
 
Seite: a = √(f/2)² + c²
Seite: b = √(f/2)² + (e-c)²
Winkel: α = arccos( (c²+a²-(f/2)²) / (2ca) )
Winkel: γ = arccos( ((e-c)²+b²-(f/2)²) / (2·(e-c)·b) )
Winkel: β = (360°-α-γ) / 2
Umfang: U = 2·(a + b)
Flächeninhalt: A = ef/2
Inkreisradius: r_i = 2A/U

Mit:
e: Symmetriediagonale
f: Zweite Diagonale
c: Abstand AP
 

 
Im Folgenden sind wesentliche Eigenschaften (Merkmale) der in diesem Unterprgramm berechenbaren und darstellbaren Vierecke aufgeführt.

 Rechteck - Eigenschaften und Merkmale:

• Zwei sich gegenüber liegende Seiten sind gleich lang und parallel
• Seine vier Innenwinkel sind gleich groß und ergänzen sich zu 360°
• Seine beiden Diagonalen sind gleich lang und halbieren einander
• Es besitzt einen Umkreis

 

Quadrat - Eigenschaften und Merkmale:

• Seine vier Seiten sind gleich lang
• Seine vier Innenwinkel sind rechte Winkel und ergänzen sich zu 360°
• Seine beiden Diagonalen sind gleich lang, stehen rechtwinklig zueinander und halbieren sich
• Der Schnittpunkt beider Diagonalen ist der Inkreismittelpunkt, der Umkreismittelpunkt und der Schwerpunkt des Quadrats

 

Drachenviereck - Eigenschaften und Merkmale:

• Seine Diagonalen stehen aufeinander senkrecht
• Seine Diagonalen halbieren sich
• Zwei einander gegenüberliegende Winkel sind gleich groß
• Es besitzt einen Inkreis

Trapez - Eigenschaften und Merkmale:
 

• Zwei seiner Seiten liegen parallel
• Ein gleichschenkliges Trapez ist symmetrisch
• Ein Trapez besitzt keinen Inkreis und keinen Umkreis
• Seine beiden parallelen Seiten ergänzen sich 180°

Parallelogramm - Eigenschaften und Merkmale:

• Seine gegenüberliegenden Innenwinkel sind gleich groß
• Seine benachbarten Winkel ergänzen sich zu 180°
• Seine gegenüberliegende Seiten sind gleich lang und schneiden sich nicht
• Seine Diagonalen halbieren einander
• Es ist punktsymmetrisch
• Jede seiner Diagonalen teilt das Parallelogramm in zwei kongruente Dreiecke
• Sein Symmetriezentrum ist der Schnittpunkt der beiden Diagonalen

Ein schiefwinkliges Parallelogramm mit ungleichen Seitenlängen hießt Rhomboid.

Raute (Rhombus, gleichseitiges Pararellogramm) - Eigenschaften und Merkmale:

• Ihre gegenüberliegende Seiten liegen parallel (jeder Rhombus ist auch ein Parallelogramm)
• Ihre gegenüberliegenden Winkel sind gleich groß
• Ihre Diagonalen stehen senkrecht aufeinander und halbieren einander
• Ihre benachbarten Winkel betragen zusammen 180°
• Jeder ihrer Innenwinkel wird durch eine Diagonale halbiert
• Ihre beiden Diagonalen sind Symmetrieachsen
• Sie besitzt einen Inkreis
• Werden die Seitenmitten eines Rechtecks miteinander verbunden, so entsteht eine Raute

  

Hinweis zum Rechteck:

Bilddiagonale (Bildschirmdiagonale): Als Bilddiagonale oder Bildschirmdiagonale wird die Strecke bezeichnet, die zwei sich gegenüberliegende Ecken eines Rechtecks verbindet. Sie wird als Maß für die Größe eines Bildschirms eingesetzt und wird mit Hilfe des nach c aufgelösten Satz des Pythagoras berechnet. Aus d² =  a² + b²  wird die Wurzel gezogen und für die Länge der Diagonale gilt: d = √a² + b², wobei a die Länge des Rechtecks beschreibt und b der Höhe dessen entspricht. Sie wird in Zoll oder Zentimetern (cm) angegeben
 

 
In einem Haus der Vierecke erfolgt die Sortierung verschiedener Vierecksarten gemäß derer gemeinsamer Eigenschaften bzw. Gemeinsamkeiten. Dies gilt insbesondere für Symmetrieeigenschaften, denn über je mehr derartiger Eigenschaften ein Viereck verfügt, desto weiter oben ist es im Haus platziert. Direkt unter dem Dach befindet sich das Quadrat, denn es besitzt die meisten dieser Symmetrieeigenschaften.
 
Ein Viereck, welches in einer höheren Etage untergebracht ist, besitzt mehr besondere Eigenschaften als ein Viereck welches in einem darunter angeordneten Stockwerk positioniert ist. Ein Viereck, welches über einem anderen angeordnet ist, besitzt wenigstens sämtliche Eigenschaften des ihm untergeordneten und mehr.

Abb.: Haus der Vierecke

 
Im Haus der Vierecke werden die verschiedenen Vierecksarten hinsichtlich ihrer folgenden Eigenschaften geordnet:

 - Seiten
 - Symmetrie
 - Winkel
 - Diagonalen

In den folgenden Tabellen sind diese Eigenschaften gemäß derer Ordnung gegliedert aufgeführt.
 
 
1. Seiten:
 

Viereck	Ein Paar gleich langer Seiten	Zwei Paare gleich langer Seiten	Alle Seiten gleiche Länge	Ein Paar paralleler Seiten	Zwei Paare paralleler Seiten
Quadrat	x	x	x	x	x
Rechteck	x	x		x	x
Raute	x	x	x	x	x
Symmetrisches Trapez	x			x
Parallelogramm	x	x		x	x
Drachenviereck	x	x
Allgemeines Trapez				x
Allgemeines Viereck

 
 
2. Symmetrie:
 

Viereck	Eine Symmetrie-achse	Zwei Symmetrie-achsen	Vier Symmetrie-achsen	Punkt-symmetrie
Quadrat	x	x	x	x
Rechteck	x	x		x
Raute	x	x		x
Symmetrisches Trapez	x
Parallelogramm				x
Drachenviereck	x
Allgemeines Trapez
Allgemeines Viereck

 

3. Winkel:
 

Viereck	Ein Paar gleich großer Winkel	Zwei Paare gleich großer Winkel	Alle Winkel sind gleich groß
Quadrat	x	x	x
Rechteck	x	x	x
Raute	x	x
Symmetrisches Trapez	x	x
Parallelogramm	x
Drachenviereck
Allgemeines Trapez
Allgemeines Viereck

 

4. Diagonalen:
 

Viereck	Beide Diagonalen sind gleich lang	Beide Diagonalen halbieren sich	Beide Diagonalen stehen senkrecht zueinander
Quadrat	x	x	x
Rechteck	x	x
Raute		x	x
Symmetrisches Trapez	x
Parallelogramm		x
Drachenviereck			x
Allgemeines Trapez
Allgemeines Viereck

  
 

Möchten Sie in diesem Unterprogramm ein Viereck berechnen und darstellen lassen, so sollten Sie folgendermaßen verfahren:
 

1. Aktivieren Sie den entsprechenden Kontrollschalter (Rechteck, Parallelogramm, Trapez, Drachenviereck) für das Viereck, mit welchem Sie Berechnungen durchführen möchten.
    
2. Definieren Sie die Werte der zur Berechnung erforderlichen Größen (siehe nachf. Aufstellung) in den entsprechenden Eingabefeldern.
    
3. Bedienen Sie die Schaltfläche Berechnen, so werden die Werte der restlichen Größen des Vierecks in der Tabelle ausgegeben.
    
4. Möchten Sie sich das Viereck grafisch darstellen lassen, so klicken Sie auf die Schaltfläche Darstellen.

 
Nicht jede Vorgabe von Eingabegrößen ermöglicht eine eindeutige Bestimmung der Werte restlicher Größen. In solch einem Fall erhalten Sie eine entsprechende Meldung. Die Schaltfläche Darstellen ist ausschließlich nach einer zuvor erfolgreich durchgeführten Berechnung bedienbar.

Möchten Sie eine neue Berechnung durchführen lassen, so klicken Sie hierfür zunächst auf die Schaltfläche Löschen und geben daraufhin die neuen Werte ein.
 

 

 

Zur Berechnung eines Rechtecks sind die Werte zweier Größen (Bestimmungsstücke) einzugeben. Dies sind:

• Seite a des Rechtecks (Quadrats)
• Seite b des Rechtecks (Quadrats)

Größenwerte die errechnet werden:

• Flächeninhalt A des Rechtecks (Quadrats)
• Diagonale e des Rechtecks (Quadrats)
• Diagonale f des Rechtecks (Quadrats)
• Diagonalenschnittpunkt P des Rechtecks (Quadrats)
• Umfang u des Rechtecks (Quadrats)
• Koordinatenwerte der Eckpunkte des Rechtecks (Quadrats)
• Schwerpunkt (Flächenschwerpunkt) S des Rechtecks (Quadrats)

 

 

Zur Berechnung eines Parallelogramms sind die Werte von genau 3 der 6 nachfolgend aufgeführten Größen (Bestimmungsstücke) einzugeben:

• Seite a des Parallelogramms
• Seite b des Parallelogramms
• Höhe h_a des Parallelogramms
• Winkel α des Parallelogramms
• Diagonale e des Parallelogramms
• Diagonale f des Parallelogramms

Größenwerte die zusätzlich errechnet werden:

• Flächeninhalt A des Parallelogramms
• Höhe h_b des Parallelogramms
• Diagonalenwinkel des Parallelogramms
• Diagonalenschnittpunkt P des Parallelogramms
• Umfang u des Parallelogramms
• Koordinatenwerte der Eckpunkte des Parallelogramms
• Schwerpunkt (Flächenschwerpunkt) S des Parallelogramms

  

 

Zur Berechnung eines Trapezes sind die Werte von genau 4 Größen (Bestimmungsstücken) einzugeben. Dies sind:

• Seite a des Trapezes
• Seite c des Trapezes
• Höhe h des Trapezes
• Winkel α des Trapezes

Größenwerte die errechnet werden:

• Flächeninhalt A des Trapezes
• Diagonale e des Trapezes
• Diagonale f des Trapezes
• Diagonalenwinkel des Trapezes
• Diagonalenschnittpunkt P des Trapezes
• Umfang u des Trapezes
• Koordinatenwerte der Eckpunkte des Trapezes
• Schwerpunkt (Flächenschwerpunkt) S des Trapezes

  

 

Zur Berechnung eines Drachenvierecks sind die Werte von genau 3 Größen (Bestimmungsstücken) einzugeben.

Dies sind:

• Seite a des Drachenvierecks
• Seite b des Drachenvierecks
• Winkel α des Drachenvierecks

Größenwerte die errechnet werden:

• Flächeninhalt A des Drachenvierecks
• Diagonale e des Drachenvierecks
• Diagonale f des Drachenvierecks
• Diagonalenwinkel des Drachenvierecks
• Diagonalenschnittpunkt P des Drachenvierecks
• Umfang u des Drachenvierecks
• Koordinatenwerte der Eckpunkte des Drachenvierecks
• Schwerpunkt (Flächenschwerpunkt) S des Drachenvierecks
• Inkreis-Mittelpunkt M des Drachenvierecks
• Inkreisradius r des Drachenvierecks
• Winkelhalbierende des Drachenvierecks

 

Als Goldenes Rechteck wird ein Rechteck bezeichnet, bei dem das Verhältnis der beiden Seiten a und b dem Goldenen Schnitt gleichkommt. Für dessen Seitenverhältnisse gilt: a:b = (a+b):a. Wird ein quadratischer Abschnitt dessen entfernt, so resultiert wiederum ein Goldenes Rechteck. Dies kann unendlich oft wiederholt durchgeführt werden und es resultiert stets ein Goldenes Rechteck.



Das Verhältnis des Goldenen Schnitts beträgt:

1 : (1+ √5) / 2 ≈ 1 : 1,618

Wird für die Länge der Seite a  der Wert a = 1 gesetzt, so ergeben sich folgende Resultate:

a = 1
a + b = 1,618
b = 0,618
   

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

   
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Anwendungsaufgaben genutzt werden.
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollschalter / Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• Alles beschriften: Punktbeschriftung und Ausgabe sonstiger Bezeichnungen des Vierecks einschalten
• Nur Punkte beschriften: Ausschließliche Punktbeschriftung des Vierecks einschalten
• Füllen: Die Farbfüllung des Vierecks ein-/ausschalten
• Details: Darstellung der des Schwerpunkts etc. des Vierecks ein-/ausschalten
• Markier.: Markierung der Eckpunkte des Vierecks ein-/ausschalten
• Diagonalen: Darstellung der Diagonalen des Vierecks ein-/ausschalten 

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Allgemeines Viereck – Interaktiv

Satz des Ptolemäus

 

Beispiel 1 - Berechnung eines Rechtecks:

Von einem Rechteck sind bekannt:

Seite: a = 4

Seite: b = 5
 

Nach einer Aktivierung des Kontrollschalters Rechteck, einer Eingabe dieser Werte in die entsprechenden Felder und einer Bedienung der Schaltfläche Berechnen, erhalten Sie die Ergebnisse für die restlichen Größen:

Diagonale: e = 6,403

Diagonale: f = 6,403

Diagonalenwinkel: 90°

Diagonalenschnittpunkt: P (2 / 2,5)

 

Umfang: U = 18

Flächeninhalt: A = 20 FE

 

Für die Koordinaten der Eckpunkte wird ausgegeben:

 

A (0 / 0)

B (4 / 0)

C (4 / 5)

D (0 / 5)

 

Schwerpunkt: S (2 / 2,5)
 

Beispiel 2 - Berechnung eines Parallelogramms:

Von einem Parallelogramm sind bekannt:

Seite: a = 2

Seite: b = 6

Winkel: α = 60°
 

Nach einer Aktivierung des Kontrollschalters Parallelogramm, einer Eingabe dieser Werte in die entsprechenden Felder und einer Bedienung der Schaltfläche Berechnen, ermittelt das Programm:

Höhe: h_a = 5,196

Höhe: h_b = 1,732

 

Diagonale: e = 7,211

Diagonale: f = 5,292

Diagonalenwinkel: 33,004°

Diagonalenschnittpunkt: P (2,5 / 2,598)

 

Umfang Parallelogramm: U = 16

Flächeninhalt Parallelogramm: A = 10,392 FE

 

Die Koordinatenwerte der Eckpunkte des Parallelogramms lauten:

 

A (0 / 0)

B (2 / 0)

C (5 / 5,196)

D (3 / 5,196)

 

Schwerpunkt: S (2,5 / 2,598)
 

Beispiel 3 - Berechnung eines Trapezes:

Von einem Trapez sind bekannt:

Seite: a = 13

Seite: c = 4

Höhe: h = 7

Winkel: α = 40°
 

Nach einer Aktivierung des Kontrollschalters Trapez, einer Eingabe dieser Werte in die entsprechenden Felder und einer Bedienung der Schaltfläche Berechnen, gibt das Programm aus:

Diagonale: e = 14,189

Diagonale: f = 8,408

Diagonalenwinkel: 85,921°

Diagonalenschnittpunkt: P (9,438 / 5,353)

 

Umfang Trapez: U = 34,921

Flächeninhalt Trapez: A = 59,5 FE

 

Für die Koordinaten der Eckpunkte des Trapezes ermittelt das Programm:

 

A (0 / 0)

B (13 / 0)

C (12,342 / 7)

D (8,342 / 7)

 

Schwerpunkt: S (8,082 / 2,882)

 

Länge der horizontalen Mittelparallele: m = 4,5

 

Beispiel 4 - Berechnung eines Drachenvierecks:

Von einem Drachenviereck sind bekannt:

Seite: a = 6

Seite: b = 12

Winkel: α = 30°
 

Nach einer Aktivierung des Kontrollschalters Drachenviereck, einer Eingabe dieser Werte in die entsprechenden Felder und einer Bedienung der Schaltfläche Berechnen, werden folgende Ergebnisse angezeigt:

Diagonale: e = 17,694

Diagonale: f = 3,105

Diagonalenwinkel: 90°

Diagonalenschnittpunkt: P (5,796 / 0)

 

Umfang: U = 36

Flächeninhalt: A = 27,478 FE

 

Die Koordinatenwerte der Eckpunkte des Drachenvierecks lauten:

 

A (0 / 0)

B (5,796 / -1,553)

C (5,796 / 1,553)

D (17,695 / 0)

 

Schwerpunkt: S (7,83 / 0)

 

Inkreis-Mittelpunkt: M (5,898 / 0)

Inkreisradius: r = 1,527

Winkelhalbierende 1: Y = -15,127·X+89,22

Winkelhalbierende 2: Y = 15,127·X-89,22
 

 

Grafische Darstellung - Beispiel 1 - Rechteck
 

Grafische Darstellung - Beispiel 2 - Rechteck


Grafische Darstellung - Beispiel 3 - Parallelogramm


Grafische Darstellung - Beispiel 4 - Parallelogramm


Grafische Darstellung - Beispiel 5 - Trapez


Grafische Darstellung - Beispiel 6 - Trapez


Grafische Darstellung - Beispiel 7 - Drachenviereck


Grafische Darstellung - Beispiel 8 - Drachenviereck

 
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Viereck
Wikipedia - Rechteck
Wikipedia - Quadrat
Wikipedia - Drachenviereck
Wikipedia - Trapez
Wikipedia - Raute
Wikipedia - Parallelogramm

 

 

Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
 

 

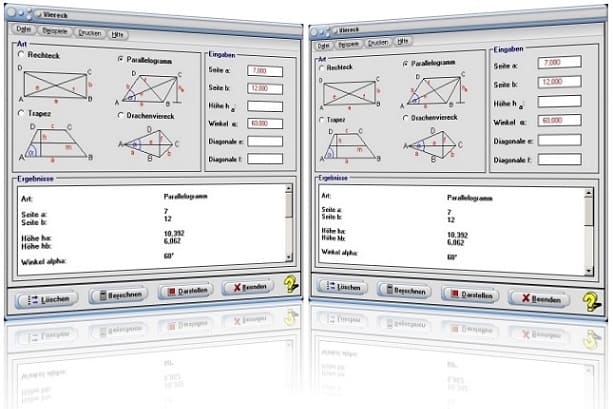
Startfenster des Unterprogramms Viereck
 

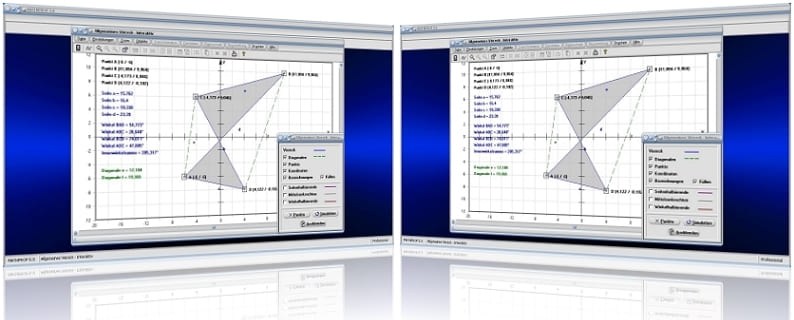
MathProf 5.0 - Unterprogramm Allgemeines Viereck

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---