MathProf - Spieker-Punkt - Mittendreieck - Spiekerpunkt - Dreieck

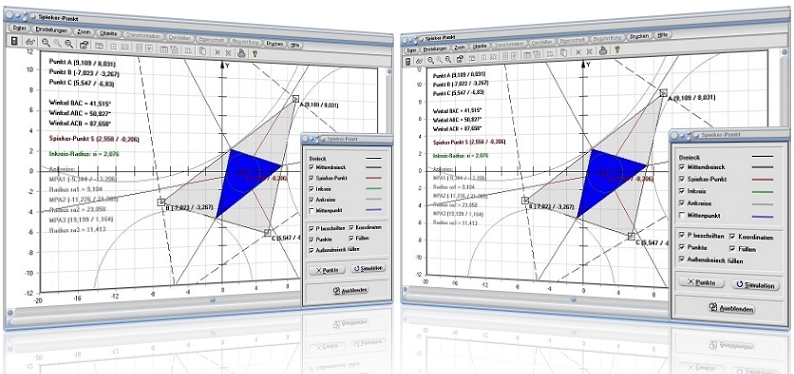
Modul Spieker-Punkt

---

 
Im Unterprogramm [Trigonometrie] - Spieker-Punkt können Untersuchungen zum Spieker-Punkt eines Dreiecks durchgeführt werden.

 

 

Gegeben sei ein Dreieck ABC. Durch die Verbindung der drei Mittelpunkte der drei Dreiecksseiten mittels Strecken entsteht das sogenannte Mittendreieck (Seitenmittendreieck). Werden die Innenwinkel des Mittendreiecks halbiert, so bildet der Schnittpunkt S dieser Winkelhalbierenden den Inkreismittelpunkt des Mittendreiecks. Er wird als Spieker-Punkt bezeichnet.

 

Der Spiekerpunkt (Spieker-Punkt) liegt mit dem Inkreismittelpunkt, dem Schwerpunkt, sowie dem Nagel-Punkt des Dreiecks auf einer Geraden. Er halbiert die Strecke zwischen dem Inkreismittelpunkt und dem Nagel-Punkt. Er ist der Schnittpunkt der drei Potenzlinien der Ankreise die die Seiten des Dreiecks berühren.

 

Dieses Programmmodul ermöglicht die Ermittlung und Darstellung des Spieker-Punkts eines allgemeinen Dreiecks. Durch eine Aktivierung des Kontrollkästchens Mittelpar. Dreieck wird das Mittelparallelen-Dreieck dargestellt. Der Spieker-Punkt, mitsamt der zugehörigen Geraden wird eingeblendet, wenn das Kontrollkästchen Spieker-Punkt aktiviert wird. Der Inkreis des Mittendreiecks wird ausgegeben, wenn Sie das Kontrollkästchen Inkreis aktivieren. Um die Ankreise des Ausgangsdreiecks darstellen zu lassen, aktivieren Sie das Kontrollkästchen Ankreise.

 

Werden die drei Ankreismittelpunkte eines Dreiecks mit den drei Seitenmittelpunkten eines Dreiecks verbunden, so schneiden sich diese im Mittenpunkt dessen. Diesen, sowie die entsprechenden Geraden können Sie sich darstellen lassen, wenn Sie das Kontrollkästchen Mittenpunkt aktivieren.

 

 

Führen Sie Folgendes aus, um Analysen zu diesem Fachthema durchzuführen:
 

1. Zur exakten Positionierung der Eckpunkte des Dreiecks klicken Sie auf die Schaltfläche Punkte auf dem Bedienformular und geben die hierfür relevanten Koordinatenwerte im daraufhin erscheinenden Formular ein. Übernommen werden diese, wenn Sie die sich dort befindende Schaltfläche Ok bedienen.
    

2. Möchten Sie die Positionen von Anfasspunkten des Dreiecks mit der Maus verändern, klicken Sie in den rechteckig umrahmten Mausfangbereich und bewegen den Mauscursor bei gedrückt gehaltener Maustaste.
    

3. Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. den Wert für die Schrittweite bzw. die Anzahl zu verwendender Winkelschritte einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

Hinweis:

Um sich detaillierte Informationen bzgl. der Eigenschaften des Dreiecks ABC ausgeben zu lassen, wählen Sie den Menüpunkt Datei - Dreieckseigenschaften. Hierauf erscheint ein Ausgabefenster mit den relevanten Daten. Um diese im *.txt-Format zu speichern, verwenden Sie den dort vorhandenden Menüeintrag Datei - Ergebnisse speichern.

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• P beschriften: Punktbeschriftung ein-/ausschalten
• Koordinaten: Anzeige der Koordinatenwerte dargestellter Punkte ein-/ausschalten
• Punkte: Darstellung von Kreismittelpunkten und Geradenschnittpunkten ein-/ausschalten
• Füllen: Farbfüllung des Mittendreiecks ein-/ausschalten
• Außendreieck füllen: Farbfüllung des Außendreiecks ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Allgemeines Dreieck aus Seitenlängen und Winkeln

Allgemeines Dreieck durch 3 Punkte

Allgemeines Dreieck – Interaktiv

 

 

Lassen Sie sich ein Dreieck darstellen, welches durch die Eckpunkte A (-8 / 8), B (-10 / -6) und C (4 / -4) beschrieben wird, so gibt das Programm (nach Aktivierung der entsprechenden Kontrollkästchen) folgende Werte aus:

 

Spieker-Punkt:

 

Punkt S (-4,5 / -0,5)

 

Ankreis 1:

 

Mittelpunkt: MPA1 (0 / -16)

Radius: ra1 = 11,314

 

Ankreis 2:

 

Mittelpunkt: MPA2 (-20 / 4)

Radius: ra2 = 11,314

 

Ankreis 3:

 

Mittelpunkt: MPA3 (10 / 14)

Radius: ra3 = 16,971

 

Inkreis-Radius des Mittendreiecks:

 

ri = 2,121

 

Innenwinkel des Dreiecks ABC:

 

Winkel BAC: 53,13°

Winkel ABC: 73,74°

Winkel ACB: 53,13°
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3
   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Spieker-Punkt zu finden.
 

 

 

Rechtwinkliges Dreieck - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck aus Seitenlängen und Winkeln - Allgemeines Dreieck durch 3 Punkte - Allgemeines Dreieck - Interaktiv - Satz des Pythagoras - Verallgemeinerung des Satz des Pythagoras - Satz des Thales - Höhensatz - Kathetensatz - Winkel am Dreieck - Innenwinkel des Dreiecks - Winkel am Kreis - Winkel an Parallelen - Sinus und Cosinus am Einheitskreis - Tangens und Cotangens am Einheitskreis - Tangentendreieck - Höhenfußpunktdreieck - Lamoen-Kreis - Taylor-Kreis - Euler-Gerade - Simson-Gerade - Satz von Ceva - Isodynamische Punkte des Dreiecks - Isogonal konjugierte Punkte - Apollonius-Punkt

 

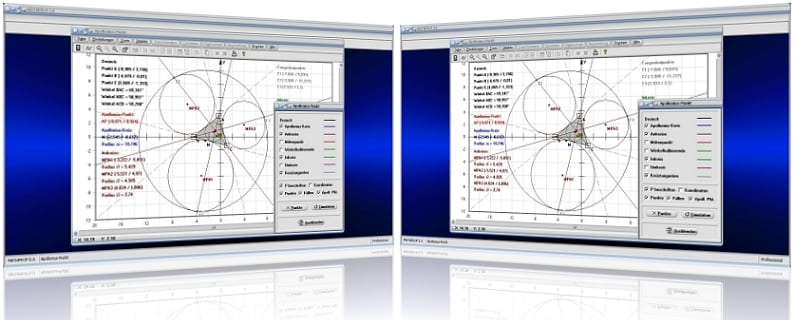
MathProf 5.0 - Unterprogramm Apollonius-Punkt

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---