MathProf - Allgemeines Dreieck - Rechner - Kosinussatz - Sinussatz

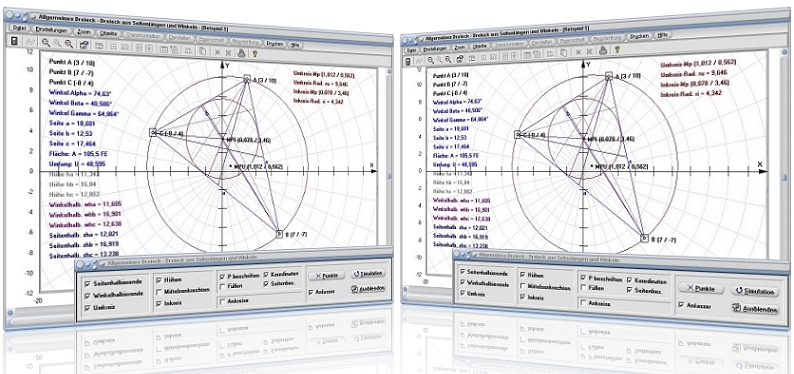
Modul Allgemeines Dreieck aus Seitenlängen und Winkeln

---

 
Mit dem Unterprogramm [Trigonometrie] -[Allgemeines Dreieck] - Allgemeines Dreieck aus Seitenlängen und Winkeln können trigonometrische Berechnungen und Untersuchungen mit allgemeinen Dreiecken durchgeführt werden, welche durch Seitenlängen und Innenwinkel beschrieben werden.

 

 
Ein allgemeines Dreieck entsteht, wenn drei beliebige, nicht auf einer Geraden liegende Punkte durch Strecken miteinander verbunden werden. Ein derartiges Dreieck wird auch als beliebiges Dreieck oder unregelmäßiges Dreieck bezeichnet.
 

  
In diesem Modul stehen sechs Größen zur Auswahl, von welchen genau drei bekannt sein müssen, um die Werte aller anderen Größen des allgemeinen Dreiecks errechnen zu können.
 

Nach der Eingabe dreier Werte der nachfolgend aufgeführten Größen können Berechnungen durchgeführt werden:

• Seite a des Dreiecks
• Seite b des Dreiecks
• Seite c des Dreiecks
• Winkel α des Dreiecks
• Winkel β des Dreiecks
• Winkel γ des Dreiecks

 
Nach der Ausführung numerischer Berechnungen werden die Werte folgender Größen eines allgemeinen Dreiecks bestimmt:

• Winkelhalbierende (Winkelsymmetrale) auf alle Seiten des Dreiecks
• Seitenhalbierende auf alle Seiten des Dreiecks
• Höhen auf alle Seiten des Dreiecks
• Inkreisradius, Inkreismittelpunkt des Dreiecks
• Umkreisradius, Umkreismittelpunkt des Dreiecks
• Ankreisradien, Ankreismittelpunkte des Dreiecks
• Umfang des Dreiecks
• Flächeninhalt des Dreiecks (Dreiecksfläche)
• Schwerpunkt (Flächenschwerpunkt) des Dreiecks

 
Es besteht zudem die Möglichkeit, die Eigenschaften des berechneten Dreiecks bei Ausgabe der grafischen Darstellung zu verändern und hierauf weitere Untersuchungen interaktiv durchzuführen.
 

Im Folgenden aufgeführt sind wesentliche besondere Punkte und besondere Linien von Dreiecken sowie deren Bezeichnungen:

• Als Höhe wird das Lot von einem Eckpunkt des Dreiecks auf die gegenüberliegende Seite dessen bezeichnet
• Die drei Höhen eines Dreiecks schneiden sich in einem Punkt, welcher als Höhenschnittpunkt bezeichnet wird
• Die Senkrechte im Mittelpunkt einer Dreiecksseite heißt Mittelsenkrechte des Dreiecks
• Die drei Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt, welcher als Umkreismittelpunkt bezeichnet wird
• Eine Gerade im Dreieck, die zu zwei Dreiecksseiten stets den gleichen Abstand besitzt, heißt Winkelhalbierende
• Die drei Winkelhalbierenden.eines Dreiecks schneiden sich in einem Punkt, welcher als Inkreismittelpunkt bezeichnet wird
• Die Verbindungsstrecke von einem Eckpunkt zum Mittelpunkt der gegenüberliegenden Seite eines Dreiecks heißt Seitenhalbierende (Schwerlinie)
• Die Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt, dem Schwerpunkt. Dieser teilt jede Seitenhalbierende im Verhältnis 2:1

Die Beschriftung eines Dreiecks erfolgt entgegen dem Uhrzeigersinn mit den Buchstaben A, B und C.
 

In dieser Auflistung aufgeführt sind wesentliche Eigenschaften von Dreiecken:

• Der größeren von zwei Seiten eines Dreiecks liegt auch der größere Winkel gegenüber
• Dem größeren von zwei Winkeln eines Dreiecks liegt auch die größere Seite gegenüber
• Die Summe zweier Seitenlängen in einem Dreieck ist stets größer als die Länge der dritten Seite
• Die Länge einer Seite eines Dreiecks ist stets größer als die Differenz der beiden anderen Seitenlängen
• Gleichgroßen Seiten eines Dreiecks liegen gleichgroße Winkel gegenüber
• Gleichgroßen Winkeln eines Dreiecks liegen gleichgroße Seiten gegenüber
• Im gleichseitigen Dreieck sind alle drei Innenwinkel gleich groß. Jeder dieser hat das Winkelmaß 60°
• Gleichseitige Dreiecke besitzen drei Symmetrieachsen
• Jedes gleichschenklige Dreieck ist axialsymmetrisch. Das von der Spitze gefällte Lot halbiert die Basis sowie den Winkel an der Spitze. Die beiden Basiswinkel sind gleich groß

Unregelmäßiges Dreieck (ungleichseitiges Dreieck): Ein Dreieck wird als unregelmäßig oder ungleichseitig bezeichnet, wenn all seine Seiten unterschiedliche Längen besitzen und all seine Winkel unterschiedliche Größen haben.
 

 
Im Weiteren gezeigt sind Abbildungen und Kurzbeschreibungen verschiedener Dreiecksarten bzw. Dreiecksformen (Übersicht):

1. Gleichseitiges Dreieck:



Abb. 1 - Gleichseitiges Dreieck

Ein gleichseitiges Dreieck ist ein Dreieck, welches drei gleich lange Seiten sowie drei gleiche Winkel von je 60° besitzt.


2. Gleichschenkliges Dreieck:



Abb. 2 - Gleichschenkliges Dreieck

Als gleichschenkliges Dreieck wird ein Dreieck bezeichnet, welches über wenigstens zwei gleich lange Seiten verfügt. Zudem sind wenigstens zwei seiner Innenwinkel gleich groß.


3. Stumpfwinkliges Dreieck:



Abb. 3 - Stumpfwinkliges Dreieck

Unter einem stumpfwinkligen Dreieck wird ein Dreieck verstanden, welches einen stumpfen Winkel besitzt. Dieser beträgt zwischen 90° und 180°. Die längste Seite dessen liegt dem stumpfen Winkel gegenüber.


4. Rechtwinkliges Dreieck:



Abb. 4 - Rechtwinkliges Dreieck 

Ein rechtwinkliges Dreieck ist ein Dreieck, welches einen rechten Winkel (90°) besitzt.


5. Spitzwinkliges Dreieck:



Abb. 5 - Spitzwinkliges Dreieck

Ein spitzwinkliges Dreieck ist ein Dreieck dessen sämtliche Innenwinkel kleiner als 90° sind.

 
6. Schiefwinkliges Dreieck:

Als schiefwinkliges Dreieck wird ein Dreieck bezeichnet, welches über keinen rechten Winkel verfügt. Es kann in die beiden Kategorien der spitzwinkligen und stumpfwinkligen Dreiecke unterteilt werden.
 

 
Nachfolgend aufgeführt finden Sie eine Gruppe von Sätzen, welche Aussagen über Dreiecke machen. Zudem sind Formeln und Fachbegriffe zu grundlegenden trigonometrischen Zusammenhängen angegeben.

Dreiecks-Kongruenzsätze (kongruente Dreiecke):

Als Kongruenzsatz wird in der Geometrie eine Aussage bezeichnet, anhand derer sich die Kongruenz von Dreiecken auf einfache Weise nachweisen lässt. Die Kongruenzsätze des Dreiecks besagen, dass ein Dreieck eindeutig berechnet werden kann, wenn eine diese Kombinationen an gegebenen Größen vorliegt:
 

• Zwei Seiten und der eingeschlossene Winkel (SWS)
• Drei Seiten (SSS)
• Eine Seite und zwei Winkel (SSW, WSW, WWS)
• Zwei Seiten und der der größeren Seite gegenüberliegende Winkel (SsW oder WsS) 

 
Dreiecksungleichungen:

Die Dreiecksungleichung besagt:
Der kleinsten Seite eines Dreiecks liegt der kleinste Winkel gegenüber. Es gilt:  a + b > c ; b + c > a ; a + c > b.

Die Dreiecksungleichung für Vektoren besagt:
Der Betrag der Summe zweier Vektoren a und b ist kleiner gleich der Summe der Beträge zweier Vektoren a und b. Es gilt:|a+b| ≤ |a|+|b|

Die umgekehrte Dreiecksungleichung für Vektoren besagt:
Der Betrag der Differenz zweier Vektoren a und b ist größer gleich der Differenz der Beträge zweier Vektoren a und b. Es gilt:|a−b|≥|a|−|b|
 
Ähnlichkeitssätze:

Hauptähnlichkeitssatz: Zwei Dreiecke sind zueinander ähnlich, wenn sie in zwei Winkeln identisch sind.

Ähnliche Dreiecke - Weitere Ähnlichkeitssätze:

Zwei Dreiecke sind zueinander ähnlich, wenn sie in allen Verhältnissen entsprechender Seiten identisch sind.
Zwei Dreiecke sind zueinander ähnlich, wenn sie in einem Winkel sowie im Verhältnis der anliegenden Seiten identisch sind.
Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis zweier Seiten sowie in dem der größeren Seite gegenüberliegenden Winkel identisch sind.
 

Winkelsummensatz (Innenwinkelsummensatz): Sind zwei Winkel eines Dreiecks bekannt, so kann der dritte hierdurch ermittelt werden. Der Winkelsummensatz (Innenwinkelsummensatz) lautet:
 
Die Winkelsumme im Dreieck beträgt 180°. Es gilt:  α + β + γ = 180°.

 
Kosinussatz:
 
Der Kosinussatz beschreibt die zwischen den drei Seiten und einem Winkel eines Dreiecks bestehenden Beziehungen. In jedem Dreieck ist das Quadrat über einer Seitenlänge gleich der Summe der Quadrate über den beiden anderen Seitenlängen vermindert um das doppelte Produkt aus diesen Seitenlängen und dem Kosinus des von ihnen eingeschlossenen Winkels. Es gilt:
 

a² = b²+c²-2bc·cos(α)
b² = a²+c²-2ac·cos(β)
c² = a²+b²-2ab·cos(γ)
 

Sinussatz:
 
Der Sinussatz stellt eine Beziehung zwischen den Winkeln eines allgemeinen Dreiecks und den gegenüberliegenden Seiten her. Im ebenen Dreieck verhalten sich die Längen von zwei Seiten wie die Sinus der gegenüberliegenden Winkel. Es gilt:
 
a/sin(α) = b/sin(β) = c/sin(γ) 

bzw.:

a/sin(α) = b/sin(β)
a/sin(α) = c/sin(γ) 
b/sin(β) = c/sin(γ) 

Tangenssatz:
 
Der Tangenssatz stellt eine Beziehung zwischen den drei Seiten eines allgemeinen Dreiecks und dem Tangens der halben Summe bzw. der halben Differenz zweier Winkel des Dreiecks her. Es gilt:

(a+b) : (a-b) = tan((α+β)/2) : tan((α-β)/2)
(a+c) : (a-c) = tan((α+γ)/2) : tan((α-γ)/2)
(b+c) : (b-c) = tan((β+γ)/2) : tan((β-γ)/2)
 

Projektionssatz:
 
c = a·cos(β)+b·cos(α)
b = c·cos(α)+a·cos(γ)
a = c·cos(β)+b·cos(α)  
 

Flächensatz:
 
Der Flächensatz besagt: Die Fläche A eines Dreiecks ist das halbe Produkt aus zwei Seiten und dem Sinus des von ihnen eingeschlossenen Winkels.

A = 1/2·a·b·sin(γ)
A = 1/2·a·c·sin(β)
A = 1/2·b·c·sin(α)
 
   
Seitenhalbierende (Schwerlinie):

Die Seitenhalbierenden s_a, s_b und s_c eines allgemeinen Dreiecks lassen sich mit Hilfe nachfolgend gezeigter Formeln berechnen.

Seitenhalbierende von a: s_a = √2·(b²+c²)-a²/2
Seitenhalbierende von b: s_b = √2·(c²+a²)-b²/2
Seitenhalbierende von c: s_c = √2·(a²+b²)-c²/2
 
Winkelhalbierende:

Die Winkelhalbierenden w_a, w_b und w_c eines allgemeinen Dreiecks können durch die im Folgenden beschriebenen Zusammenhänge ermittelt werden.

Winkelhalbierende w_a von α:  2·b·c·cos (α/2) / (b+c)
Winkelhalbierende w_b von β:  2·c·a·cos (β/2) / (a+c)
Winkelhalbierende w_c von γ:  2·a·b·cos (γ/2) / (a+b)

Höhen:

Die Höhen h_a, h_b und h_c eines allgemeinen Dreiecks können wie folgt berechnet werden.

Höhe h_a = b·sin (γ) = c·sin (β)
Höhe h_b = c·sin (α) = a·sin (γ)
Höhe h_c = a·sin (β) = b·sin (α)

Inkreis:

Der Inkreismittelpunkt ist der Schnittpunkt der Winkelhalbierenden des Dreiecks. Sein Radius kann wie folgt berechnet werden:


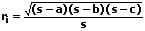
mit:



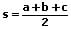
Umkreis:

Der Umkreismittelpunkt ist der Schnittpunkt der Mittelsenkrechten des Dreiecks. Sein Radius kann wie folgt berechnet werden:



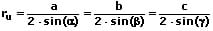
Schwerpunkt:

Der Schwerpunkt S(xs,ys) eines Dreiecks aus den drei Punkten P1(x1;y1), P2(x2;y2), P3(x3;y3) ist der Schnittpunkt der drei Seitenhalbierenden. Für seine Koordinaten gilt:

xs = (x1+x2+x3)/3
ys = (x1+x2+x3)/3

Dreiecksfläche - Parallelogramm:

Die Fläche eines Dreiecks entspricht der Fläche eines halben Parallelogramms und kann somit auch wie folgt berechnet werden:

A = 1/2·ha
A = 1/2·hb
A = 1/2·hc

h_a: Höhe h_a des Dreiecks
h_b: Höhe h_b des Dreiecks
h_c: Höhe h_c des Dreiecks
 

Heronsche Flächenformel (Heronsche Dreiecksformel - Satz des Heron):
 
s = (a + b +c)/2

Fläche: A = √s·(s-a)·(s-b)·(s-c)
 
Die Heronsche Flächenformel kann zur Berechnung der Fläche eines allgemeinen Dreiecks verwendet werden. Der Satz des Heron beschreibt die mathematische Formel, mit deren Hilfe der Flächeninhalt eines Dreiecks aus den drei Seitenlängen berechenbar ist. Diese Formel wird auch als Heronsche Formel oder Heronsche Dreiecksformel bezeichnet.
 

Trigonometrische Flächenformel:
 
Die trigonometrische Flächenformel besagt: Der Flächeninhalt eines schiefwinkligen Dreiecks ist gleich dem halbierten Produkt zweier seiner Seiten und dem Sinuswert des Winkels, den diese Seiten einschließen. Es gilt für den Flächeninhalt eines Dreiecks:

A = a·b·sin(γ)/2 = b·c·sin(α)/2 = a·c·sin(β)/2

Flächenverhältnis:
 
Für das Flächenverhältnis zweier Dreiecke gilt: Die Flächen zweier ähnlicher Dreiecke verhalten sich wie die Quadrate entsprechender Seiten oder Transversalen.

A₁ : A₂ = s₁² : s₂²

A₁,A₂: Flächen der Dreiecke
s₁,s₂: Transversalen der Dreiecke

Oben Beschriebenes gilt auch für Vielecke.

Streckenverhältnis:
 
Die Umfänge zweier ähnlicher Dreiecke verhalten sich wie die entsprechenden Seiten oder Transversalen.

u₁ : u₂ = s₁ : s₂

u₁,u₂: Umfänge der Dreiecke
s₁,s₂: Transversalen der Dreiecke
 
Oben Beschriebenes gilt auch für Vielecke.

Basiswinkel:

Als Basiswinkel werden die gleichgroßen Winkel eines gleichschenkligen Dreiecks bezeichnet.

Basiswinkelsatz:

In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.

Basislinie:

Als Basislinie wird die der Spitze eines gleichschenkligen Dreiecks gegenüberliegende Seite bezeichnet.

Goniometrische Gleichungen:

Goniometrische Gleichungen (trigonometrische Gleichungen) sind Gleichungen, in denen mindestens eine Variable im Argument von Winkelfunktionen vorkommt.

Ortslinien:
 
Linien, deren Punkte durch eine gemeinsame, geometrische Eigenschaft gekennzeichnet sind, werden als Ortslinien (geometrische Orte) bezeichnet. Hierzu zählen unter anderem der Kreis und die Gerade (z.B. Winkelhalbierende, Seitenhalbierende, Inkreis und Umkreis eines Dreiecks).

Erste Winkelhalbierende - zweite Winkelhalbierende: Als erste bzw. zweite Winkelhalbierende werden die in einem zweidimensionalen kartesischen Koordinatensystem die beiden Geraden bezeichnet, die den zwischen der x- und y-Achse des Systems vorhandenen Winkel halbieren.

Winkelgröße: Eine Winkelgröße gibt die Größe eines Winkels an. Sie beschreibt den den Richtungsunterschied zweier sich in einem Punkt treffender Schenkel.

Besondere Dreiecke: Als besondere Dreiecke werden oftmals rechtwinklige Dreiecke, gleichschenklige Dreiecke und gleichseitige Dreiecke bezeichnet.

Teildreieck: Als Teildreieck wird ein Dreieck bezeichnet, welches auf eine beliebige Art aus einer anderen geometrischen Figur ausgeschnitten wurde.
  

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

   
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Anwendungsaufgaben genutzt werden.
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

   

Grafische Darstellung - Beispiel 1
 

Grafische Darstellung - Beispiel 2

 
 
Gehen Sie folgendermaßen vor, um ein allgemeines Dreieck, von welchem drei der o.a. Größen bekannt sind, berechnen zu lassen und anschließend weitere Untersuchungen interaktiv durchzuführen:
 

1. Geben Sie die Werte dreier o.a. Größen in die entsprechenden Felder ein und lassen Sie alle anderen Felder leer. Bedienen Sie ggf. zuvor die Taste Löschen.
    
2. Nach einem Klick auf die Schaltfläche Berechnen gibt das Programm die ermittelten Resultate in einer Tabelle aus.
    
3. Um sich das Dreieck grafisch ausgeben zu lassen, bedienen Sie die Schaltfläche Darstellen. Es wird das Dreieck dargestellt, welches durch Eingabewerte definiert wurde.
    
4. Lassen Sie sich bei Bedarf Seitenhalbierende, Winkelhalbierende, Umkreis, Höhe, Mittelsenkrechten, Inkreis und Ankreise durch die Aktivierung entsprechender Kontrollkästchen darstellen.
    
5. Sollen die Eigenschaften des berechneten Dreiecks interaktiv verändert werden und das gesamte Dreieck mittels Mausoperationen bewegt werden, so aktivieren Sie zunächst das Kontrollkästchen Anfasser, klicken anschließend in den rechteckig umrahmten Mausfangbereich einer Markierung und bewegen den Mauscursor bei gedrückt gehaltener Maustaste.
    
6. Sollen die Koordinatenwerte einzelner Punkte verwendet werden, so können Sie die Schaltfläche Punkte auf dem Bedienformular bedienen und die entsprechenden Werte im daraufhin erscheinenden Formular eingeben. Übernommen werden diese, wenn Sie die sich dort befindende Schaltfläche Ok bedienen.
    
7. Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. die zu verwendenden Werte für Schrittweite bzw. Verzögerung einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

Hinweise : 

Wurden die Werte zu weniger oder zu vieler Größen eingegeben, so erhalten Sie eine Fehlermeldung. Eine weitere Voraussetzung zur Durchführbarkeit von Berechnungen ist, dass mit den eingegebenen Größen ein Dreieck eindeutig bestimmt werden kann - ist dies nicht der Fall, so wird eine Fehlermeldung ausgegeben. Durch bestimmte Werteingaben kann es vorkommen, dass ein Dreieck nicht eindeutig beschrieben werden kann. Es wird hierbei aber stets eine der möglichen Lösungen ausgegeben und dargestellt. Die Schaltfläche Darstellen ist ausschließlich nach einer zuvor erfolgreich durchgeführten Berechnung bedienbar.

 

Um sich detaillierte Informationen bzgl. der Eigenschaften des Dreiecks bei dessen Darstellung anzeigen zu lassen, wählen Sie den Menüpunkt Datei - Dreieckseigenschaften. Hierauf erscheint ein Ausgabefenster mit den relevanten Daten. Um diese im *.txt-Format zu speichern, verwenden Sie den dort vorhandenden Menüeintrag Datei - Ergebnisse speichern.

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Bei Ausgabe der grafischen Darstellung wird Ihnen nachfolgend gezeigtes Bedienformular zur Verfügung gestellt, mit welchem Sie die Möglichkeit haben weitere Untersuchungen mit einem Dreieck durchzuführen. Durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen können Sie folgende zusätzliche Einstellungen vornehmen, die bei Ausgabe der grafischen Darstellung wirksam werden:

 

 

• Seitenhalbierende: Ein-/Ausblendung der Seitenhalbierenden des Dreiecks
• Winkelhalbierende: Ein-/Ausblendung der Winkelhalbierenden des Dreiecks
• Umkreis: Ein-/Ausblendung des Umkreises des Dreiecks
• Höhe: Ein-/Ausblendung der Höhe des Dreiecks
• Mittelsenkrechten: Ein-/Ausblendung der Mittelsenkrechten des Dreiecks
• Inkreis: Ein-/Ausblendung des Inkreises des Dreiecks
• Ankreise: Ein-/Ausblendung der Ankreise des Dreiecks
   
• P beschriften: Beschriftung der Mausfangpunkte des Dreiecks ein-/ausschalten
• Koordinaten: Anzeige der Koordinaten des Mausfangpunktes und der Eckpunkte des Dreiecks ein-/ausschalten
• Füllen: Farbfüllung der Dreiecksfläche ein-/ausschalten
• Seitenbez.: Seitenbezeichnung des Dreiecks ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Allgemeines Dreieck durch 3 Punkte

Allgemeines Dreieck – Interaktiv

 

 
Von einem beliebigen Dreieck seien die Werte folgender Größen bekannt:

Seitenlänge: a = 1

Seitenlänge: c = 3

Innenwinkel: β = 30°
 

Nach Eingabe dieser in die entsprechenden Felder und einer Bedienung der Schaltfläche Berechnen erhalten Sie die Werte für die restlichen Größen des Dreiecks:

Seitenlänge: b = 2,192

 

Innenwinkel: α = 13,187°

Innenwinkel: γ = 136,813°

 

Höhe ha = 1,5

Höhe hb = 0,684

Höhe hc = 0,5

 

Flächeninhalt des Dreiecks: A = 0,75 FE

Umfang des Dreiecks: U = 6,192

 

Radius des Inkreises: ri = 0,242

Mittelpunkt des Inkreises: MI (2,096 / 0,242)

 

Radius des Umkreises: ru = 2,192

Mittelpunkt des Umkreises: MU (1,5 / -1,598)

 

Länge der Winkelhalbierende auf Seite a: wa = 2,516

Länge der Winkelhalbierende auf Seite b: wb = 1,449

Länge der Winkelhalbierende auf Seite c: wc = 0,505

 

Länge der Seitenhalbierende auf Seite a: sa = 2,579

Länge der Seitenhalbierende auf Seite b: sb = 1,949

Länge der Seitenhalbierende auf Seite c: sc = 0,807

 

Radius des Ankreises auf Seite a: ra = 0,358

Mittelpunkt des Ankreises auf Seite a: MPA (3,096 / 0,358)

 

Radius des Ankreises auf Seite b: rb = 0,83

Mittelpunkt des Ankreises auf Seite b: MPB (-0,096 / 0,83)

 

Radius des Ankreises auf Seite c: rc = 7,822

Mittelpunkt des Ankreises auf Seite c: MPC (0,904 / -7,822)

 

Die Ortskoordinatenwerte der Eckpunkte A, B und C des Dreiecks werden ausgegeben mit:

 

A (0 / 0)

B (3 / 0)

C (2,134 / 0,5)

 

Der Schwerpunkt des Dreiecks besitzt die Koordinatenwerte: S (1,711 / 0,167)
 

 

Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6


Grafische Darstellung - Beispiel 7
  

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Dreieck
Wikipedia - Inkreis
Wikipedia - Umkreis
Wikipedia - Ankreis
Wikipedia - Sinussatz
Wikipedia - Kosinussatz
 

 

Rechtwinkliges Dreieck - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck durch 3 Punkte - Allgemeines Dreieck - Interaktiv - Satz des Pythagoras - Verallgemeinerung des Satz des Pythagoras - Satz des Thales - Höhensatz - Kathetensatz - Winkel am Dreieck - Innenwinkel des Dreiecks - Winkel am Kreis - Winkel an Parallelen - Sinus und Cosinus am Einheitskreis - Tangens und Cotangens am Einheitskreis - Tangentendreieck - Höhenfußpunktdreieck - Lamoen-Kreis - Taylor-Kreis - Euler-Gerade - Simson-Gerade - Satz von Ceva - Isodynamische Punkte des Dreiecks - Isogonal konjugierte Punkte - Spieker-Punkt - Apollonius-Punkt
 

 

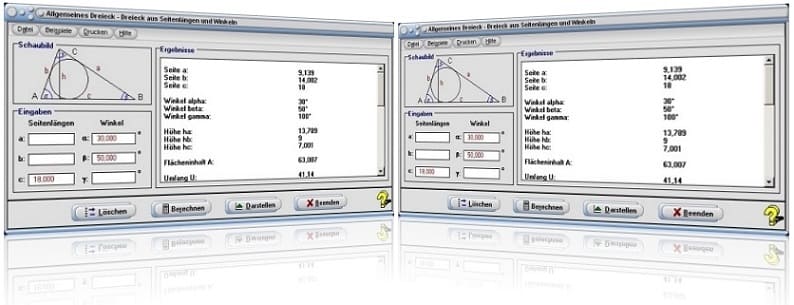
Startfenster des Unterprogramms Allgemeines Dreieck aus Seitenlängen und Winkeln
 

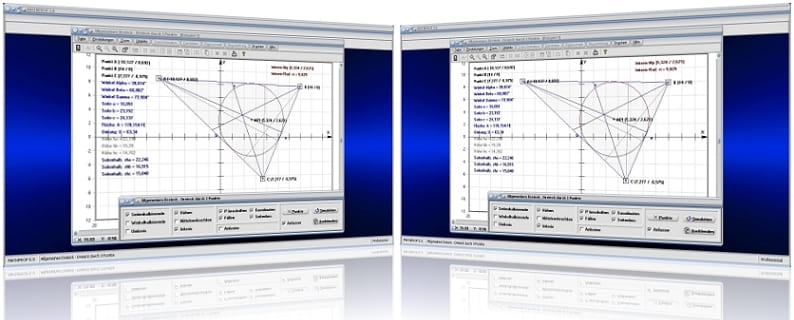
MathProf 5.0 - Unterprogramm Allgemeines Dreieck durch 3 Punkte

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---