
Kurzinfos zum
Themengebiet Algebra
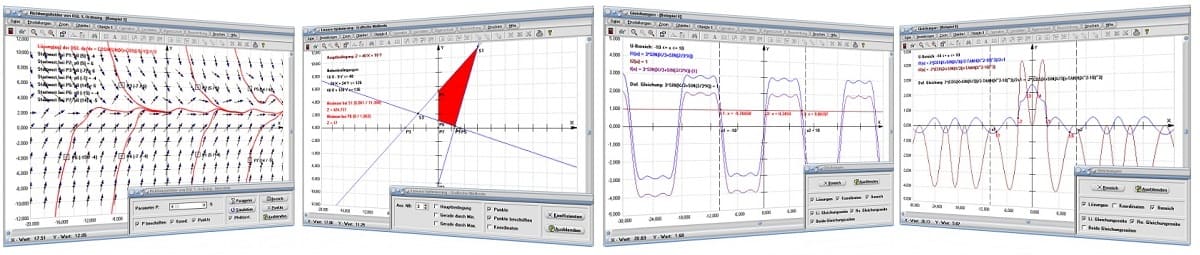
Nachfolgend aufgeführt finden Sie Bilder und Kurzbeschreibungen zu
einigen Modulen, die im Programm MathProf 5.0 unter dem
dem Hauptmenüpunkt Algebra implementiert sind.
• Matrizen
1. Operationen mit Matrizen reeller Zahlen
- Transponierung einer Matrix reeller Zahlen
- Invertierung einer Matrix reeller Zahlen
- Potenzierung einer Matrix reeller Zahlen
- Faktorisierung einer Matrix reeller Zahlen
- Multiplikation einer Matrix reeller Zahlen mit einer reellen Zahl
- Ermittlung des Werts der Determinante einer Matrix reeller Zahlen
- Bildung des Exponentials einer Matrix reeller Zahlen
- Singulärwertzerlegung einer Matrix (SVD) reeller Zahlen
- Ermittlung der Eigenschaften einer Matrix reeller Zahlen (Norm, Rang, Dimension, maximales und minimales Element, Summe der Diagonalelemente)
- Ermittlung der Eigenwerte und Eigenvektoren einer Matrix reeller Zahlen
- Ermittlung des minimalen und maximalen Eigenwerts einer Matrix reeller Zahlen
- Addition zweier Matrizen reeller Zahlen
- Subtraktion zweier Matrizen reeller Zahlen
- Multiplikation zweier Matrizen reeller Zahlen
- Division zweier Matrizen reeller Zahlen
- Multiplikation einzelner Elemente zweier Matrizen reeller Zahlen
- Division einzelner Elemente zweier Matrizen reeller Zahlen
- Transponierung einer Matrix komplexer Zahlen
- Invertierung einer Matrix komplexer Zahlen
- Potenzierung einer Matrix komplexer Zahlen
- Faktorisierung einer Matrix komplexer Zahlen
- Multiplikation einer Matrix mit einer reellen Zahl oder einer komplexen Zahl
- Ermittlung des Werts der Determinante einer Matrix komplexer Zahlen
- Bildung des Exponentials einer Matrix komplexer Zahlen
- Ermittlung der Eigenschaften einer Matrix komplexer Zahlen (Norm, Rang, Dimension, maximales und minimales Element, Summe der Diagonalelemente)
- Ermittlung der Eigenwerte und Eigenvektoren einer Matrix komplexer Zahlen
- Addition zweier Matrizen komplexer Zahlen
- Subtraktion zweier Matrizen komplexer Zahlen
- Multiplikation zweier Matrizen komplexer Zahlen
- Division zweier Matrizen komplexer Zahlen
- Multiplikation einzelner Elemente zweier Matrizen komplexer Zahlen
- Division einzelner Elemente zweier Matrizen komplexer Zahlen
• Gaußscher Algorithmus
• Lineare Optimierung
• Simplex-Methode
• Gleichungen
• Ungleichungen - Prinzip
• Gleichungen 2.- 4. Grades
• Richtungsfelder von Differentialgleichungen
• Differentialgleichungen 1. Ordnung
• Differentialgleichungssystem
• Mengenelemente
• Venn-Diagramm
- Bildung des Durchschnitts von Mengen
- Bildung der Vereinigung von Mengen
- Bildung der Differenz von Mengen
- Bildung der symmetrischen Differenz von Mengen
- Bildung der Komplementmenge bzgl. der Grundgesamtheit
• Zahluntersuchung
- ganzzahliger Teiler der Zahlen A und B
- der Anzahl ganzzahliger Teiler der Zahlen A und B
- der Summe der Zahlen A und B
- des ggT (größten gemeinsamen Teilers der Zahlen A und B)
- des kgV (kleinsten gemeinsamen Vielfachen der Zahlen A und B)
- des Quotienten der Zahlen A und B
- ganzzahligen Rests bei Division der Zahlen A und B
- des Produkts der Zahlen A und B
- Anzahl derer Teiler
- Teilersumme
- Echtteilersumme
- Teiler
• Einheitskreis komplexer Zahlen
• Addition und Subtraktion komplexer Zahlen
• Multiplikation und Division komplexer Zahlen
• Zahlen II
- Partitionen
- Perrin-Zahlen
- Undulierende Zahlen
- Multiplikative Beharrlichkeit
- k-Permutationen
- Quasibefreundete Zahlen
- Zeckendorf-Zerlegung
- Gray-Code
- Biquadratische Quadrupel
- Abundante und defiziente Zahlen
• Binomische Formel
• Irrationale Zahlen
• Wurzellupe und Dezimalbruch


Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gaußscher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL - Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
Weitere relevante Seiten zu diesem Programm

 |  |
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.


























































