MathProf - Binomialkoeffizient - Pascalsches Dreieck - Formel

Fachthemen: Binomialkoeffizient - Pascalsches Dreieck

MathProf - Stochastik - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen zur Erlangung des Wissens der Grundlagen der Statistik für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das kleine Modul zur numerischen Berechnung der Binomialkoeffizienten natürlicher Zahlen und zur Analyse der Zusammenhänge beim Pascalschen Dreieck.

Beispiele, welche Aufschluss zur Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind implementiert.

 

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.
 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

 

Themen und Stichworte zu diesem Modul: Pascalsches Dreieck - Binomialkoeffizient - Tabelle - Berechnen - n - k - Pascal - Dreieck - 3 über 2 - 4 über 2 - 4 über 3 - 5 über 2 - 5 über 3 - 6 über 2 - 6 über 3 - 7 über 3 - 7 über 4 - 7 über 5 - 7 über 6 - 8 über 2 - 9 über 3 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - Über - Werte - Binomisch - Rechner - Wahrscheinlichkeit - Beispiel - Formeln - Fakultät - Taschenrechner - Koeffizient - Anwendung - Addieren - Darstellung - Elemente - Zahlen - Kombinatorik - Schreibweise - Stochastik - Statistik - Binomische Formeln - Binom - Binomial - Grundlagen - Summe - Rechenregeln - Eigenschaften - Graph - Multiplizieren - Formel - Begriff - Begriffe - Was sind - Was ist - Welche - Welcher - Welches - Wodurch - Wieviel - Wie viele - Einführung - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Beschreibung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Mathe - Mathematik - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Herleitung - Beweis - Anwendungsaufgaben - Definition - Lösungen - Summe - Diagonalen - Zeilen - Berechnung - Summe der Binomialkoeffizienten

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.
 

 

 

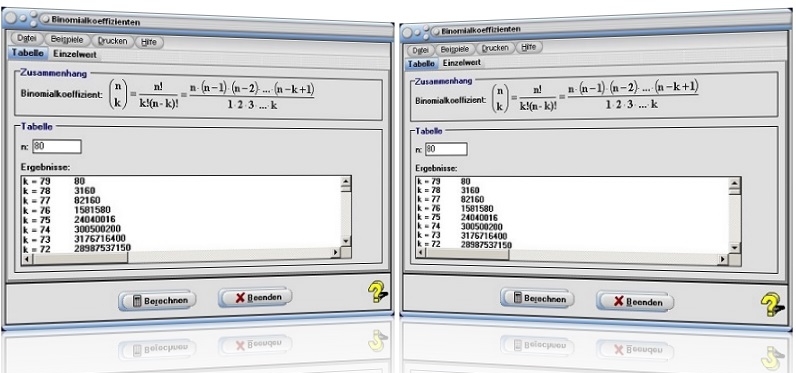
Modul Binomialkoeffizienten

Der Binomialkoeffizient gibt an, wie viele Möglichkeiten bestehen aus einer Menge von n Elementen, ohne Berücksichtigung der Reihenfolge sowie ohne Zurücklegen, k verschiedene Elemente auszuwählen. Er findet unter anderem bei der Bestimmung der Wahrscheinlichkeitsfunktion einer Binomialverteilung Anwendung und wird in nachfolgend aufgeführter Form dargestellt (Formel):
 

Binomialkoeffizienten werden durch die beiden natürlichen Zahlen n und k (sprich: n über k) gebildet können nach der rekursiven Bildungsvorschrift des bekannten Pascalschen Dreiecks ermittelt werden.

Beispiele für die Werte einiger Binomialkoeffizienten sind nachfolgend aufgeführt:

5 über 3 = 10
7 über 2 = 21
7 über 4 = 35
9 über 4 = 126

Die Binomialkoeffizienten b von 20 über k mit k = 0...n lauten beispielsweise:

k    b(20,k)

0    1
1    20
2    190
3    1140
4    4845
5    15504
6    38760
7    77520
8    125970
9    167960
10    184756
11    167960
12    125970
13    77520
14    38760
15    15504
16    4845
17    1140
18    190
19    20
20    1

Beispiel zur Anwendung des Binomialkoeffizienten (Kombinatorik):

Bei der Ziehung der Lottozahlen werden von 49 nummerierten Kugeln aufeinanderfolgend 6 Kugeln gezogen (ohne Zurücklegen). Wieviele Möglichkeiten bestehen 6 Zahlen auszuwählen?

Die Anzahl der Kugeln beträgt: n = 49
Die Anzahl der Ziehungen beträgt: k = 6

A = n! / ( (n - k)! · k! ) = 49! / ( (49 - 6)! · 6! ) = 13983816

Dies bedeutet: Es existieren 13983816 mögliche Kombinationen und die Wahrscheinlichkeit 6 Richtige zu ziehen beträgt demnach 1 zu 13.983.816.

Im Weiteren aufgeführt sind einige besondere Eigenschaften des Binomialkoeffizienten sowie Regeln zur Durchführung der Berechnung von Binomialkoeffizienten. Diese werden als Rechenregeln für Binomialkoeffizienten bezeichnet und lauten wie folgt:
 
Regel 1:



Regel 2:



Regel 3:



Regel 4:


  

Das Pascalsche Dreieck ist eine grafische Zahlenanordnung in Dreiecksform, mit welchem sich Binomialkoeffizienten bestimmen lassen. Binomialkoeffizienten sind in diesem Dreieck so angeordnet, dass jeder Zahleneintrag der Summe der beiden darüberstehenden Einträge entspricht. Durch Addition zweier benachbarter Zahlen entsteht die darunter stehende Zahl (siehe rote Markierung in oben angeordneter Darstellung). Das besagte Dreieck ermöglicht es, beliebige Potenzen von Binomen auf einfache Weise auszumultiplizieren. Es kann beliebig erweitert werden. Den Koeffizienten n über k findet man in der Zeile n+1 an der Stelle k+1.

Konstruktion des Pascalschen Dreiecks:

Das Pascalsche Dreieck kann konstruiert werden, indem oben mit der Zahl 1 begonnen wird. Hierauf wird die darunterliegende Zeile mit zwei Einsen versehen. Es wird eine weitere Zeile hinzugefügt und die jeweils außen angeordneten Zeilen werden mit einer Eins versehen. Die restlichen einzubindenden Zahlen werden durch die Addition der beiden oberhalb von ihr liegenden Zahlen gebildet. Dieses Schema wird fortgesetzt bis die gewünschte Dimension dieses Dreiecks erreicht ist.

Mit seiner Hilfe lässt sich das Lösungsschema für binomische Formeln der Form (a+b)ⁿ bzw. (a-b)ⁿ herleiten. Die ersten dieser lauten:
 
(a + b)² = a² + 2ab + b²
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a - b)² = a² - 2ab + b²
(a - b)³ = a³ - 3a²b + 3ab² - b³
(a - b)⁴ = a⁴ - 4a³b + 6a²b² - 4ab³ + b⁴
  
Dieses angewandte Schema gibt die Zahlen an, die in der binomischen Formel als Koeffizienten vor den entsprechenden Variablen stehen. Wie oben dargestellt, besitzt dieses Lösungsschema für binomische Formeln mit den Exponenten 2, 3 und 4 die nachfolgend gezeigte Form.
 
Zeile 2: Exponenten des Binoms mit n = 2:  1 - 2 - 1
Zeile 3: Exponenten des Binoms mit n = 3:  1 - 3 - 3 - 1
Zeile 4: Exponenten des Binoms mit n = 4:  1 - 4 - 6 - 4 - 1
 

Um sich in diesem Modul alle Binomialkoeffizienten über einen bestimmten Wertebereich von n berechnen zu lassen, sollten Sie Folgendes ausführen:
 

1. Wählen Sie das Registerblatt Tabelle und definieren Sie im dafür vorgesehenen Eingabefeld den ganzzahligen Wert für n.
    
2. Bedienen Sie die Schaltfläche Berechnen, so werden die entsprechenden Ergebnisse in der sich darunter befindenden Tabelle ausgegeben.

 
Möchten Sie lediglich einen bestimmten Binomialkoeffizienten ermitteln lassen, so wählen Sie das Registerblatt Einzelwert, geben die entsprechenden Werte für n und k in die dafür zur Verfügung stehenden Felder ein und bedienen die Schaltfläche Berechnen.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema  der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs  (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
 
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
  

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

Binomialverteilung

Galton-Brett

 
Sollen alle Binomialkoeffizienten für n = 8 ausgegeben werden, so erhält man nach Eingabe des Werts 8 und einer Bedienung der Schaltfläche Berechnen:
 

Beispiel 1


Beispiel 2
 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Binomialkoeffizient zu finden.

Kombinatorik - Urnenmodell - Pfadregel - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Regressionsanalyse - Stichproben - Stichproben - Verteilungen - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)

MathProf 5.0 - Unterprogramm Binomialverteilung

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

Unsere Produkte

 
Nachfolgend aufgeführt finden Sie Kurzinfos zu den von uns entwickelten Produkten.

 

I - MathProf 5.0
Mathematik interaktiv
 

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.
 

 

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
 

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Analysis
• Kurzinfos zum Themengebiet Geometrie
• Kurzinfos zum Themengebiet Algebra
• Kurzinfos zum Themengebiet 3D-Mathematik
• Kurzinfos zum Themengebiet Stochastik
• Kurzinfos zum Themengebiet Vektoralgebra
• Kurzinfos zum Themengebiet Trigonometrie
• Kurzinfos zu sonstigen Themengebieten

---

 

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in MathProf implementierten Modulen finden Sie, indem Sie den Reiter MathProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 

II - PhysProf 1.1
Physik interaktiv
 

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.
 

 

Durch die Benutzung dieses Programms wird es ermöglicht, bereits bekannte Fachthemeninhalte aufzuarbeiten und entsprechende Sachverhalte numerisch wie auch grafisch zu analysieren. Mittels der freien Veränderbarkeit der Parameter von Einflussgrößen bei der Ausgabe grafischer Darstellungen besteht in vielen Unterprogrammen die Möglichkeit, Veränderungen an dargestellten Zusammenhängen manuell oder durch die Anwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
 

Eine Übersicht aller in PhysProf 1.1 zur Verfügung stehender Programmteile finden Sie im PhysProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Kurzinfos zu Inhalten einiger Unterprogramme von Physprof 1.1 erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Mechanik
• Kurzinfos zum Themengebiet Elektrotechnik
• Kurzinfos zum Themengebiet Optik
• Kurzinfos zum Themengebiet Thermodynamik
• Kurzinfos zu sonstigen Themengebieten

---

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in PhysProf implementierten Modulen finden Sie, indem Sie den Reiter PhysProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
 

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

 

 
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
 

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

---

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.