MathProf - Stellenwertsysteme - Dezimalsystem - Binärsystem

Fachthema: Stellenwertsysteme - Zahlensysteme

MathProf - Algebra - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Umwandlung von Zahlen in andere Stellenwertsysteme mit unterschiedlicher Basis.

Der in diesem Teilprogramm implementierte Rechner ermöglicht das Umrechnen bzw. die Konvertierung der Zahlen verschiedener Zahlensysteme in andere. Hierzu zählen neben vielen weiteren, das Dualsystem, das Ternärsystem, das Oktalsystem, das Hexadezimalsystem sowie das Dezimalsystem.

Die Ausgabe der Binärzahlen, Oktalzahlen, Hexadezimalzahlen, Dezimalzahlen und anderer erfolgt in einer Tabelle.

Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität dieses Programmmoduls geben, sind eingebunden.

 

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.
 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

 

Themen und Stichworte zu diesem Modul: Zahlensysteme - Zahlensystem - Basis - Umrechnen - Umrechner - Umwandler - Umwandlung - Konvertieren - Umwandeln - Zahlentabelle - Stellenwerte - Wandler - Stellenwertsysteme - Konverter - Wandlung - Binär - Dual - Oktal - Binärzahlen - Dualzahlen - Dezimalzahlen - Hexadezimalzahlen - Oktalzahlen - Hexadezimalzahl - Dezimalzahl - Dualzahl - Binärzahl - Oktalzahl - Dezimale - Berechnen - Rechnen - Berechnung - Definition - Einführung - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Ergebnis - Lösungen - Aufgaben - Rechensysteme - Dualsystem - Zweiersystem - Dreiersystem - Vierersystem - Fünfersystem - Hexadezimalsystem - Sechsersystem - Binärsystem - Achtersystem - Oktalsystem - Zehnersystem - Polyadische Zahlensysteme - Polyadisches Zahlensystem - Positionssystem - Positionssysteme - Buchstaben - Ziffern - Dezimalsystem - Hex umrechnen - Dualdarstellung - Binär umrechnen - Binäre Darstellung - Binärdarstellung - Oktal umrechnen - Zahl - Ziffer - Tabelle - Liste - Zahlen - Beispiel - Grundlagen - Bestimmen - Übersicht - Erklärung - Beschreibung - Herleitung - Beweis - Begriff - Begriffe - Wie viel - Wieviel - Welche - Welcher - Welches - Wodurch - Definition - Rechner - Basis - Zur Basis - Basis 2 - Basis 3 - Basis 4 - Basis 5 - Basis 6 - Basis 7 - Basis 8 - Basis 9 - Basis 10 - Basis 11 - Basis 12 - Basis 13 - Basis 14 - Basis 15 - Basis 16 - Basis 17 - Basis 18 - Basis 19 - Basis 20 - Basis 21 - Basis 22 - Basis 24 -Basis 26 - Basis 28 - Basis 30 - Basis 32 - Basis 36 - 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - A - B - C - D - E - F - G - H - I - K - L - M - N - P - R - S - 11 - 10 - 01 - 111 - 001 - 100 - 010 - 22 - 33 - 44 - System - Dezimalzahlen umrechnen - Zahlenumwandlung - Beispiele - Ternärsystem - Binärzahlen umrechnen - Dualzahlen umrechnen - Hexadezimaldarstellung - Dezimaldarstellung - Oktaldarstellung - Binärdarstellung - Hexadezimal-Umrechner - Umrechner für Binärzahlen - Rechner für binäre Zahlen - Rechner für duale Zahlen

  

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.
 

  

Modul Zahlumwandlung

 
Das Programmmodul [Algebra] - [Zahlensysteme] - Zahlumwandlung ermöglicht die Umwandlung (das Konvertieren bzw. Umrechnen) der Zahlen eines Stellenwertsystems in andere.

 
Unter einem Stellenwertsystem (Positionssystem) wird ein Zahlensystem verstanden, bei dem jeder Stelle einer Zahl ein eigener Wert zugeordnet wird. Zu den meist verwendeten Stellenwertsystemen zählen das Binärsystem (Dualsystem) sowie das Dezimalsystem (Zehnersystem).
 
Zu den, außer dem Dezimalsystem, am häufigsten benötigten Stellenwertsystemen dürften das Dual-, des Hexadezimal- und das Oktalsystem gehören.

Mit Hilfe dieses Unterprogramms ist es möglich, eine Zahl in 36 verschiedene Stellenwertsysteme umwandeln bzw. umrechnen zu lassen.

Nachfolgend aufgeführt ist eine Übersicht über die meist gebrauchten Stellenwertsysteme.

- Als Dualsystem (Zweiersystem oder Binärsystem) wird ein Stellenwertsystem zur Basis 2 bezeichnet. Es besteht lediglich aus den beiden Ziffern 0 und 1 und ist eines der am häufigsten verwendeten Zahlensysteme (Rechensysteme).
- Als Ternärsystem (Dreiersystem) wird ein Stellenwertsystem zur Basis 3 bezeichnet.
- Als Fünfersystem wird ein Stellenwertsystem zur Basis 5 bezeichnet.
- Als Sechsersystem wird ein Stellenwertsystem zur Basis 6 bezeichnet.
- Als Achtersystem (Oktalsystem) wird ein Stellenwertsystem zur Basis 8 bezeichnet.
- Als Dezimalsystem (Zehnersystem oder Positionszahlensystem mit der Basis zehn) wird ein Stellenwertsystem zur Basis 10 bezeichnet. Es handelt sich um das weltweit meist benutzte Zahlensystem.
- Als Duodezimalsystem wird ein Stellenwertsystem zur Basis 12 bezeichnet.
- Als Hexadezimalsystem wird ein Stellenwertsystem zur Basis 16 bezeichnet.


Zahldarstellungen im Dualsystem werden als Dualzahlen oder Binärzahlen bezeichnet.
Zahldarstellungen im Oktalsystem werden Oktalzahlen genannt.
Zahldarstellungen im Dezimalsystem werden als Dezimalzahlen bezeichnet.
Zahldarstellungen im Duodezimalsystem werden als Duodezimalzahlen bezeichnet.
Zahldarstellungen im Hexadezimalsystem werden als Hexadezimalzahlen bezeichnet.
 
Desweiteren gezeigt ist eine kleine Zahlentabelle, welche die dezimalen Zahlen 0 - 15 in einigen der oben aufgeführten Zahlensysteme in umgewandelter Form ausgibt.
 

 
In einer weiteren Tabelle sind die Bezeichnungen, Stellenwerte und Ziffern einzelner Zahlensysteme mit der Basis von 2 bis 12 sowie 16 gelistet. Bei Zahlensystemen mit einer Basis größer 10 werden Buchstaben verwendet um zweistellige Zahlen darzustellen, da die Ziffern 0-9 hierfür nicht mehr ausreichen. Als Stellenwerte werden die Werte bezeichnet, welche die Ziffern einer Zahl hinsichtlich ihrer Position besitzen. Jede Ziffer einer Zahl steht für einen bestimmten Stellenwert.
 

1. Beispiel der Umrechnung einer Dualzahl (Binärzahl) in das Zehnersystem:
   (Umrechnung einer Zahl vom Dualsystem (Binärsystem) in das Zehnersytem



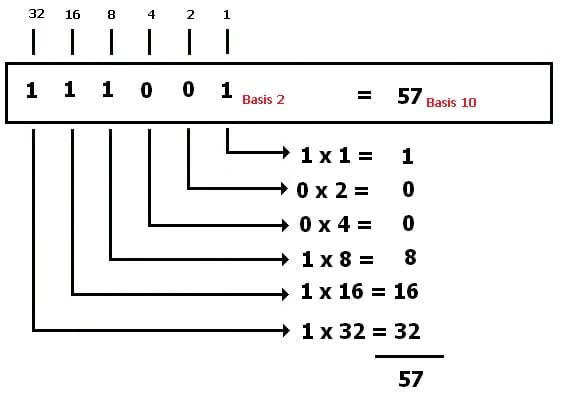
Bei der Umrechnung einer Dualzahl (Binärzahl) in das Dezimalsystem wird jede Ziffer bei einer bestimmten Stelle mit dem zugehörigen Stellenwert des Dualzahlystems multipliziert. Hierauf wird die Summe der durchgeführten Multiplikationen gebildet. Diese ergibt den Wert der Zahl, den diese im Dezimalsystem besitzt.

2. Beispiel der Umrechnung einer Hexadezimalzahl in das Zehnersystem:



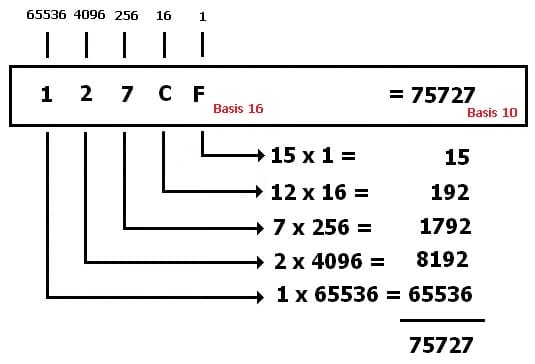
Bei der Umrechnung einer Hexadezimalzahl in das Dezimalsystem wird jede Ziffer bei einer bestimmten Stelle mit dem zugehörigen Stellenwert des Hexadezimalsystems multipliziert. Hierauf wird die Summe der durchgeführten Multiplikationen gebildet. Diese ergibt den Wert der Zahl, den diese im Dezimalsystem besitzt.

Um Berechnungen in diesem Modul durchführen zu lassen, tragen Sie zunächst die zu wandelnde Zahl im entsprechend gültigen Format in das Feld Zahl ein. Selektieren Sie hierauf aus der aufklappbaren Auswahlbox Basis, in welches Stellenwertsystem die entsprechende Zahl gewandelt werden soll. Bedienen Sie hierauf die Schaltfläche Berechnen, so gibt das Programm die Darstellung dieser Zahl in allen zur Verfügung stehenden Stellenwertsystemen (Basen) aus.

Hinweis:

Geben Sie die Zahl im entsprechend gültigen (in der Auswahlbox eingestellten) Format ein, ansonsten quittiert das Programm die Durchführung einer Wandlung mit der Ausgabe einer Fehlermeldung. Stellenwertsysteme mit Basen größer 10 verwenden die Zeichen A,B,C,D ...V.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

Zahlensysteme

Möchten Sie sich die Dualzahl 101001011 in andere Stellenwertsysteme gewandelt ausgeben lassen, so wählen Sie in der Auswahlbox Basis den Eintrag 2, geben in das Feld Zahl die Zeichenfolge 101001011 ein und bedienen die Schaltfläche Berechnen. Das Programm wandelt diese Zahl hierauf in andere Stellenwertsysteme und gibt aus:

Stellenwertsystem    Zahl

2                           101001011
3                           110021
4                           11023
5                           2311
6                           1311
7                           652
8                           513
9                           407
10                         331   (Dezimalzahl)
11                         281
12                         237
13                         1C6
14                         199
15                         171
16                         14B
17                         128
18                         107
19                          H8
20                          GB
21                          FG
22                          F1
23                          E9
24                          DJ
25                          D6
26                          CJ
27                          C7
28                          BN
29                          BC
30                          B1
31                          AL
32                          AB
33                          A1
34                          9P
35                          9G
36                          97

Beispiel 1
 

Beispiel 2


Beispiel 3


Beispiel 4


Beispiel 5

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Stellenwertsystem
Wikipedia - Zahlensystem
Wikipedia - Dezimalsystem
Wikipedia - Dualsystem

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte

MathProf 5.0 - Unterprogramm Zahlensysteme

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

Unsere Produkte

 
Nachfolgend aufgeführt finden Sie Kurzinfos zu den von uns entwickelten Produkten.

 

I - MathProf 5.0
Mathematik interaktiv
 

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.
 

 

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
 

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Analysis
• Kurzinfos zum Themengebiet Geometrie
• Kurzinfos zum Themengebiet Algebra
• Kurzinfos zum Themengebiet 3D-Mathematik
• Kurzinfos zum Themengebiet Stochastik
• Kurzinfos zum Themengebiet Vektoralgebra
• Kurzinfos zum Themengebiet Trigonometrie
• Kurzinfos zu sonstigen Themengebieten

---

 

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in MathProf implementierten Modulen finden Sie, indem Sie den Reiter MathProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 

II - PhysProf 1.1
Physik interaktiv
 

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.
 

 

Durch die Benutzung dieses Programms wird es ermöglicht, bereits bekannte Fachthemeninhalte aufzuarbeiten und entsprechende Sachverhalte numerisch wie auch grafisch zu analysieren. Mittels der freien Veränderbarkeit der Parameter von Einflussgrößen bei der Ausgabe grafischer Darstellungen besteht in vielen Unterprogrammen die Möglichkeit, Veränderungen an dargestellten Zusammenhängen manuell oder durch die Anwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
 

Eine Übersicht aller in PhysProf 1.1 zur Verfügung stehender Programmteile finden Sie im PhysProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Kurzinfos zu Inhalten einiger Unterprogramme von Physprof 1.1 erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Mechanik
• Kurzinfos zum Themengebiet Elektrotechnik
• Kurzinfos zum Themengebiet Optik
• Kurzinfos zum Themengebiet Thermodynamik
• Kurzinfos zu sonstigen Themengebieten

---

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in PhysProf implementierten Modulen finden Sie, indem Sie den Reiter PhysProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
 

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

 

 
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
 

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

---

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.