MathProf - Umrechnung - Winkelmaße - Bogenmaß - Winkelmaß - Radiant

Fachthemen: Winkelmaße - Gradmaß - Bogenmaß

MathProf - Geometrie - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für den Rechner zur Umrechung verschiedener Winkelmaße in andere.

In diesem Unterprogramm kann unter anderem die Umwandlung der Winkel vom Gradmaß ins Bogenmaß (Radiant) und in gon (Neugrad) sowie umgekehrt ausgeführt werden.

Zudem können die zwischen Winkeleinheiten am Einheitskreis bestehenden Zusammenhänge mit Hilfe einer grafischen Darstellung nachvollzogen werden.

Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind implementiert.

 

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.
 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

 

Themen und Stichworte zu diesem Modul: Bogenmaß - Gradmaß - Winkelmaße - Winkelmaß - Gradmaß und Bogenmaß - Winkel - Minuten - Sekunden - Winkelangabe - Winkelangaben - Winkelrechner - Radiant - Winkelminute - Winkelsekunde - Grad - Rad - Deg - Gon - Neugrad - Altgrad - Degree - Rechner - Umrechnung - Umwandlung - Angabe - Abkürzung - Einheit - Einheiten - Bestimmen - Bestimmung - Winkelmesser - Winkel messen - Einheitskreis - Kreis - Umrechnen - Winkel umrechnen - Bogenmaß berechnen - Winkel in Grad - Winkel in rad - Bogenmaß in Grad - Grad in Bogenmaß - Gradangabe - Gradangaben - Gradzahl - Gradzahlen - Bogenmaß eines Winkels - Winkel in deg - Winkel in gon (Neugrad) - Grad in gon - Gon in Grad - Minute - Sekunde - Winkeleinheit - Vollwinkel - Umrechnen - Berechnen - Umrechnung - Umrechnungsformel - 30 Grad - 45 Grad - 60 Grad - 90 Grad - 120 Grad - 270 Grad - Pi/6 - Pi/4 - Pi/3 - Pi/2 - Pi - 2Pi - 90° in Bogenmaß - 90° in rad - 45° in Bogenmaß - 45° in rad - 60° in Bogenmaß - In Grad - In Rad - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 15 - 20 - 30 - 45 - 60 - 75 - 90 - 100 - 120 - 150 - 180 - 200 - 270 - 300 - 360 - 60° in rad - 90° in Bogenmaß - 90° in rad - 180° in Bogenmaß - 180° in rad - 270° in Bogenmaß - 270° in rad - Darstellung - Durchmesser - Formeln - Winkeleinheiten - Ermitteln - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Bedeutung - Wie - Was bedeutet - Welche - Welcher - Welches - Wodurch - Erklärung - Einfach erklärt - Übungsaufgaben - Üben - Übungen - Einführung - Lösungen - Zusammenhang - Aufgaben - Formeln - Länge - Pi - Positiver Winkel - Negativer Winkel - Rechter Winkel - Rechten Winkel berechnen - Tabelle - Liste - Drehung - Berechnung - Formel - Berechnungsformel - Beschreibung - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Definition - Mathe - Mathematik - Physik - Zeichnen - Begriff - Begriffe - Darstellen - Graph - Plot - Plotter - Kreisbogen - Bogenlänge - Bogen - Bogenminute - Bogensekunde - Dezimalgrad - Umrechnen - Winkelminuten - Winkelsekunden - Bogenminuten - Bogensekunden - Winkelgrad

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.
 

   

 

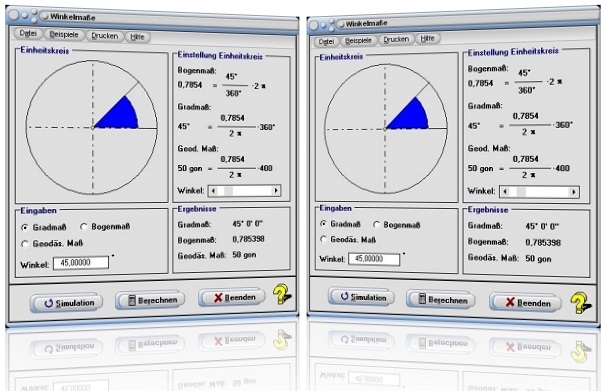
Modul Winkelmaße

 
Mit Hilfe des kleinen Unterprogramms [Geometrie] - [Sonstiges (2D)] - Winkelmaße kann die Umrechnung verschiedener Winkelmaße in andere durchgeführt werden.

Winkelmaß (Gradmaß): Winkelmaße beruhen auf der gleichmäßigen Teilung des Kreises. Als Grundeinheit wurde das Gradmaß (Deg) festgelegt. Ein Gradmaß erhält man durch ist die Teilung eines Kreises durch Radien in deckungsgleiche Teile (Kreissektoren). Hierbei wird ein Kreis durch Radien in 360 gleiche Teile zerlegt. Der Richtungsunterschied zweier Radien, die vom Kreismittelpunkt zu benachbarten Teilen des Kreises führen besitzen die Maßeinheit 1 Grad (Winkelgrad). Das Winkelmaß wird zur Angabe der Winkelweite eines Winkels in der Ebene in der Mathematik und Physik eingesetzt.

Bogenmaß: Das Verhältnis der Länge des Kreisbogens b zum Radius des Kreises r wird als Bogenmaß bezeichnet. Das Bogenmaß besitzt die Einheit Radiant, abgekürzt rad. Es ergibt sich aus Bogenlänge/Radius = b/r = π·α / 180°. 1 rad ist der Winkel, für welchen das Verhältnis der Längen von Bogen zu Radius gleich 1 ist (es ist das Verhältnis der Länge des zu diesem Winkel gehörenden Kreisbogens b und des Kreisradius r). 1 rad = (180/π)° = 57,29578°. Beim Bogenmaß handelt es sich um ein Winkelmaß, bei dem ein Winkel durch die Länge des entsprechenden Kreisbogens im Einheitskreis angegeben wird.
 
Gradangaben: Beim Grad (Winkelgrad) handelt es sich um eine Hilfsmaßeinheit für den Größenwert eines ebenen Winkels.

Winkelangaben: Bei einer Winkelangabe handelt es sich um die Angabe einer Winkelweite eines ebenen Winkels. Sie findet Anwendung in der Mathematik und der Physik als als physikalische Größe.

Winkelminuten - Winkelsekunden: Ein Grad (Dezimalgrad) entspricht dem 360-ten Teil des Vollwinkels des Kreises. Der 60-te Teil eines Grades ist die Minute (Winkelminute). Sie ist eine Unterteilung der Maßeinheit Grad und dient zur Angabe der Größe ebener Winkel. Der 60-te Teil einer Winkelminute ist die Winkelsekunde.

Bogenminuten: Die Bogenminute ist der 60-te Teil eines Winkelgrads. Sie entspricht der Winkelminute.
Bogensekunden: Die Bogensekunde ist der 60-te Teil und der einer Winkelminute und der 3600-te Teil eines Winkelgrads. Sie entspricht der Winkelsekunde.

Radiant: Beim Radiant handelt es sich um ein Winkelmaß, bei dem der Winkel durch die Länge des entsprechenden Kreisbogens im Einheitskreis festgelegt wird.

Gradzahl: 1 Grad ist definiert als der 360. Teil des Vollwinkels (1 Vollwinkel = 360°). Ein Grad entspricht dem 360-sten Teil eines Kreises.
 
Gon: Die Maßeinheit Gon wird in der Geodäsie verwendet. Sie ergibt sich durch die Zerlegung des Kreises in 400 gleiche Teile. Früher wurde das Gon in 100 Neuminuten zu jeweils 100 Neusekunden unterteilt und als als Neugrad bezeichnet. Das Neugrad wurde früher zur Unterscheidung vom üblichen Grad (Degree) verwendet, welcher daraufhin als Altgrad bezeichnet wurde.
 
Winkeleinheiten: Als Winkeleinheit wird die Maßeinheit für Winkelmessungen in der Ebene, auf der Kugel oder einem Kreis bezeichnet.

Rechter Winkel: Als rechter Winkel, wird ein Winkel von 90° bezeichnet. Er ist der vierte Teil eines Vollwinkels zu 360°.
 
Winkel messen: Ein Winkelmesser ist ein Messinstrument zur Bestimmung (zum Erfassen) von Winkeln oder zum Eintragen eines Winkels. Er besteht aus einer kreisförmigen oder halbkreisförmigen Scheibe, die über eine Winkeleinteilung verfügt.
 

Gradmaß - Bogenmaß:

Für die Umrechnung eines Gradmaßes in ein Bogenmaß (Radiant) x gilt:

Bogenmaß - Gradmaß:

Für die Umwandlung eines Winkelmaßes x vom Bogenmaß (Radiant) in ein Gradmaß gilt:

Gradmaß - Geodäsisches Maß:

Für die Umwandlung eines Winkelmaßes x vom Gradmaß in ein Geodäsisches Maß gilt:

Positiver Winkel - Negativer Winkel:
 
Bei der Drehung eines Punkts am Kreis gegen den Uhrzeigersinn wird der Winkel als positiv bezeichnet. Bei einer Drehung in umgekehrter Richtung ist dieser negativ.
 

Durch die Aktivierung des Kontrollschalters Gradmaß, Bogenmaß oder Geodäs. Maß legen Sie fest, in welchem Format das umzuwandelnde Winkelmaß eingegeben wird. Nach der Eingabe eines Werts in das Feld Winkel und einer Bedienung der Schaltfläche Berechnen gibt das Programm die ermittelten Ergebnisse aus.

Durch eine Bedienung des Schiebereglers Winkel werden alle Winkel im Bereich von 0° - 360° am Einheitskreis im Gradmaß mit einer Schrittweite von 1° berechnet und die Ergebnisse der Umrechnungsformen ausgegeben.

Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt. Hierauf können Sie ggf. den Wert für die zu verwendende Verzögerung einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Simulation wieder durch eine Bedienung der Schaltfläche Sim. Stop.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Awendungsaufgaben genutzt werden. Dieses Programm kann auch dabei behilflich sein, einen Begriff zum entsprechenden Fachthema zu erklären.
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

Beispiel 1:

Es gilt, die im Gradmaß vorliegende Winkelgröße 112,56° in andere umwandeln zu lassen.

Vorgehensweise und Lösung:

Nach einer Aktivierung des Kontrollschalters Gradmaß, der Eingabe des o.a. Zahlenwerts in das dafür vorgesehene Feld und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:

Gradmaß: 112° 33' 36'' (im Format "Grad, Minuten, Sekunden")

Bogenmaß (Radiant): 1,964543

Geodäs. Maß: 125,067 gon
 

Beispiel 2:

Es ist die im Bogenmaß vorliegende Winkelgröße 1,25 in andere umzuwandeln.

Vorgehensweise und Lösung:

Nach einer Aktivierung des Kontrollschalters Bogenmaß, der Eingabe des o.a. Zahlenwerts in das dafür vorgesehene Feld und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:

Gradmaß: 71° 37' 10'' (im Format "Grad, Minuten, Sekunden")

Bogenmaß (Radiant): 1,25

Geodäs. Maß: 79,57747 gon
  

Beispiel 1


Beispiel 2

   

Beispiel 3


Beispiel 4


Beispiel 5
 

Hilfreiche Informationen zu diesem Fachthema sind unter der Adresse Wikipedia - Winkelmaße und Wikipedia - Radiant zu finden.
 

Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)

MathProf 5.0 - Unterprogramm Interaktive Geometrie mit Objekten

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

Unsere Produkte

 
Nachfolgend aufgeführt finden Sie Kurzinfos zu den von uns entwickelten Produkten.

 

I - MathProf 5.0
Mathematik interaktiv
 

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.
 

 

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
 

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Analysis
• Kurzinfos zum Themengebiet Geometrie
• Kurzinfos zum Themengebiet Algebra
• Kurzinfos zum Themengebiet 3D-Mathematik
• Kurzinfos zum Themengebiet Stochastik
• Kurzinfos zum Themengebiet Vektoralgebra
• Kurzinfos zum Themengebiet Trigonometrie
• Kurzinfos zu sonstigen Themengebieten

---

 

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in MathProf implementierten Modulen finden Sie, indem Sie den Reiter MathProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 

II - PhysProf 1.1
Physik interaktiv
 

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.
 

 

Durch die Benutzung dieses Programms wird es ermöglicht, bereits bekannte Fachthemeninhalte aufzuarbeiten und entsprechende Sachverhalte numerisch wie auch grafisch zu analysieren. Mittels der freien Veränderbarkeit der Parameter von Einflussgrößen bei der Ausgabe grafischer Darstellungen besteht in vielen Unterprogrammen die Möglichkeit, Veränderungen an dargestellten Zusammenhängen manuell oder durch die Anwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
 

Eine Übersicht aller in PhysProf 1.1 zur Verfügung stehender Programmteile finden Sie im PhysProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Kurzinfos zu Inhalten einiger Unterprogramme von Physprof 1.1 erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Mechanik
• Kurzinfos zum Themengebiet Elektrotechnik
• Kurzinfos zum Themengebiet Optik
• Kurzinfos zum Themengebiet Thermodynamik
• Kurzinfos zu sonstigen Themengebieten

---

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in PhysProf implementierten Modulen finden Sie, indem Sie den Reiter PhysProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
 

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

 

 
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
 

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

---

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.