MathProf - Nadelproblem - Zahlengenerator - Pythagoreische Tripel - Zufall

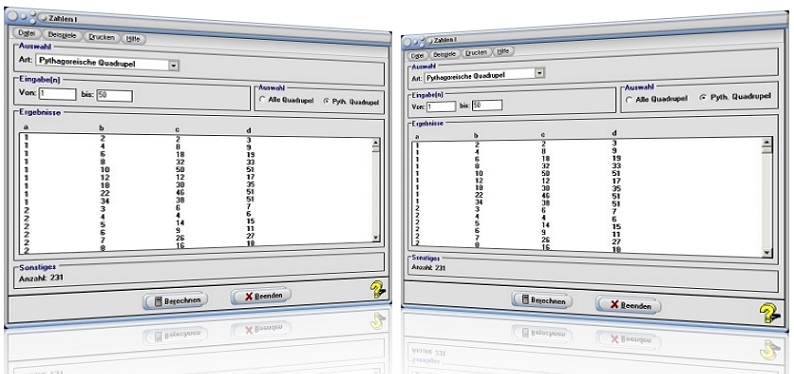
Modul Zahlen I

---

Das Unterprogramm [Algebra] - [Zahlen] - Zahlen I ermöglicht das Berechnen der Werte verschiedener spezieller Zahlen.
 

 

 
In diesem Modeul können Berechnungen durchgeführt werden mit:
 

• Heronsche Wurzelformel (Heron-Verfahren)
• Pythagoreische Zahlentripel (Pythagoreische Tripel)
• Kreiszahl Pi
• Leibniz-Formel
• Zufallszahlen 1
• Zufallszahlen 2
• Buffonsches Nadelexperiment (Buffonsches Nadelproblem)
• Zahlenfolge 3a+1
• Wallis-Formel
• Beinahe Pythagoreische Tripel
• Pythagoreische Quadrupel
• Quadratfreie Zahlen
• Bernoulli-Zahlen

  

 


 
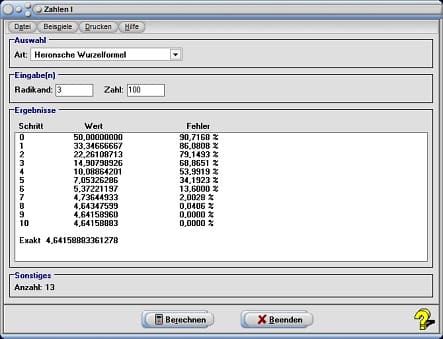
Die iterative Berechnung der beliebigen Wurzel einer Zahl nach Heron können Sie durchführen lassen, indem Sie den Eintrag Wurzelformel Heron aus der aufklappbaren Auswahlbox wählen, die Werte für den Radikanden, sowie den Wurzelexponenten in die dafür vorgesehenen Felder Radikand und Zahl eintragen und hierauf die Schaltfläche Berechnen bedienen. Es werden alle Zwischenlösungen bis zum Erreichen eines bestimmten Fehlerwertes ausgegeben. Die Formel zur iterativen Errechnung von Wurzeln wird als Heron'sche Wurzelformel bezeichnet und besitzt die Form:

 

 
Eine Berechnung des Werts ³√5, die über 5 Schritte hinweg ausgeführt wird, liefert folgende Ergebnisse:

Schritt 0:  2,5000000000

Schritt 1:  1,9333333333

Schritt 2:  1,7347866297

Schritt 3:  1,7103290941

Schritt 4:  1,7099760196

Schritt 5:  1,7099759467
 

Der exakte Wert (nicht mit dieser Methode errechnet) dieser Zahl lautet: 1,7099759466767
 

 


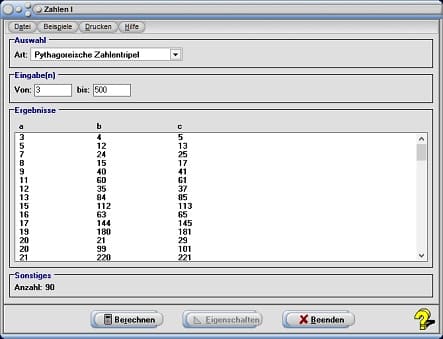
Pythagoreische Zahlentripel sind die Tripel natürlicher Zahlen a, b, c, welche die Bedingung a² + b² = c² erfüllen.

Ein derartiges Tripel errechnet sich aus den Zusammenhängen:

a = u·v

b = (u² - v²)/2

c = (u² + v²)/2
 

unter der Voraussetzung, dass u und v teilerfremd sind und diese natürliche, ungerade Zahlen sind.

Nachdem Sie den Eintrag Pythagoreische Zahlentripel gewählt haben, den zu untersuchenden Zahlenbereich in den Eingabefeldern Von und Bis definierten und die Schaltfläche Berechnen bedienten, ermittelt das Programm derartige Tripel.

Möchten Sie Details bzgl. der Eigenschaften eines rechtwinkligen Dreiecks erfahren, welches die Seitenlängen a,b und c besitzt, so fokussieren Sie den entsprechenden Tabelleneintrag und bedienen hierauf die Schaltfläche Eigenschaften. 
 

 
Über einen Wertebereich von 3 bis 20 erhalten Sie folgende Tripel:

a	b	c
3	4	5
5	12	13
8	15	17

Für die Eigenschaften des Pythagoreischen Dreiecks mit den Seitenlängen

a = 8
b = 15
c = 17

erhalten Sie darüber hinaus folgende Informationen:

Winkel α = 28,072°
Winkel β = 61,928°
Winkel γ = 90°

Länge der Seitenhalbierende sha = 15,524
Länge der Seitenhalbierende shb = 10,966
Länge der Seitenhalbierende shc = 8,5

Länge der Winkelhalbierende wha = 15,462
Länge der Winkelhalbierende whb = 9,330
Länge der Winkelhalbierende whc = 7,379

Höhe h_a = 1
Höhe h_b = 8
Höhe h_c = 7,059

Fläche A = 60
Umfang U = 40
Inkreisradius r_i = 3
Umkreisradius r_u = 8,5
 

 


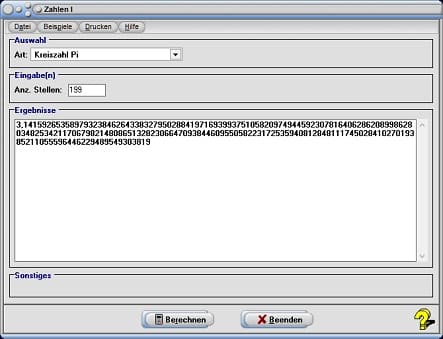
Nach einer Auswahl des Eintrags Kreiszahl Pi aus der aufklappbaren Auswahlbox, der Festlegung der Nachkomma-Stellengenauigkeit im Eingabefeld Anz. Stellen und der Bedienung der Schaltfläche Berechnen wird die Kreiszahl Pi auf die angegebene Anzahl von Nachkommastellen (bis max. 10000) ermittelt und ausgegeben.
 

 
Nach der Festlegung einer Anzahl von Nachkommastellen von 40, erhalten Sie folgendes Ergebnis:

π = 3,1415926535897932.....
 

 

 
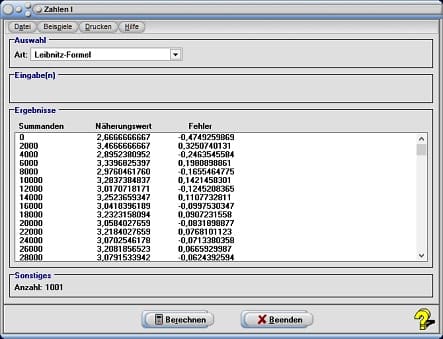
Im Jahre 1682 steuerte Gottfried Wilhelm Leibniz der Suche nach einer bestmöglichen Annäherung an die Kreiszahl Pi folgende Regel (auch als Leibniz-Reihe bekannt):

1 – 1/3 + 1/5 – 1/7 + 1/9 ... = π/4

Hierbei erhöht sich der Wert des Nenners eines jeden Summanden im Vergleich zum vorherigen, um jeweils 2.

Da dieses Verfahren eine langsame Konvergenzgeschwindigkeit aufweist, bedarf es der Nutzung vieler Schritte um einen guten Näherungswert für die Zahl π zu erreichen. Dies können Sie untersuchen, wenn Sie den Eintrag Leibniz-Formel aus der aufklappbaren Auswahlbox und hierauf die Schaltfläche Berechnen bedienen. Das Programm addiert die entsprechenden Summanden und gibt die ermittelten Zwischensummen derer, nach jeweils 2000 durchgeführten Berechnungen, aus.

Die prozentuale Abweichung der Werte der Zwischenergebnisse zu einem sehr genauen Wert für π wird jeweils nach Durchführung der vorgegebenen Anzahl von Berechnungen ausgegeben.
 

 


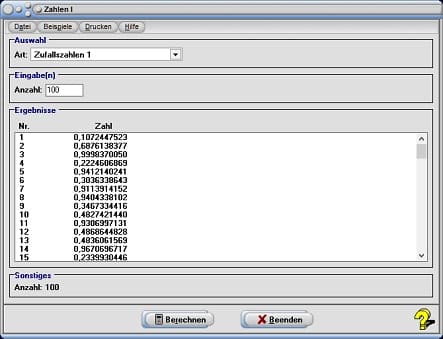
Unter Zufallszahlen 1 werden Zufallszahlen von einem Zufallsgenerator im Bereich von 0 bis 1 erzeugt und nach einer Bedienung des Schalters Berechnen ausgegeben. Die Anzahl zu erzeugender Zufallszahlen kann durch Eingabe eines ganzzahligen Werts in das hierfür vorgesehene Feld Anzahl festgelegt werden.
 

 


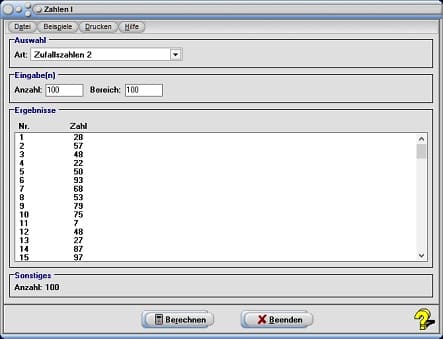
Zufallszahlen finden unter anderem Anwendung bei statistischen Versuchen, bei Codierungen, in der Kryptographie sowie bei Glücksspielen und Wetten.

Der Einsatz von einem Zufallszahlengenerator (Zufallsgenerator bzw. Zahlengenerator) ermöglicht es, Zufallszahlen aus einem frei festlegbaren Zahlenbereich ermitteln zu lassen. Es handelt sich hierbei um eine Menge ganzer Zahlen. Ein Generator für Zufallszahlen kann beispielsweise zur Erzeugung von Lotteriezahlen verwendet werden. Die Wahrscheinlichkeit 6 Richtige aus 49 zu erzeugen liegt jedoch bei einer Wahrscheinlichkeit von 1: 13.983.816.
 
Wird der Eintrag Zufallszahlen 2 aus der aufklappbaren Auswahlbox gewählt, so werden durch einen Zufallsgenerator ganzzahlige Zufallszahlen erzeugt, die innerhalb eines Bereichs von 0 bis zum, im Eingabefeld Bereich festgelegten, Wert liegen. Nach einer Bedienung des Schalters Berechnen werden die Zufallszahlen ausgegeben. Die Anzahl zu erzeugender Zufallszahlen ist im entsprechenden Eingabefeld Anzahl festzulegen.
 

 


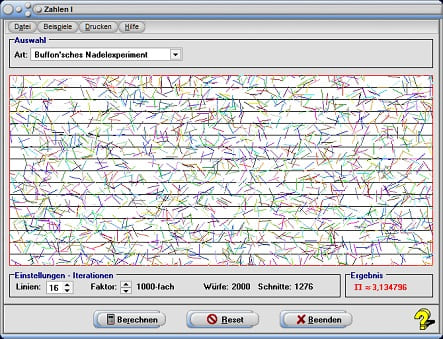
Durch eine Selektion des Eintrags Buffon'sches Nadelexperiment aus der aufklappbaren Auswahlbox können Sie sich dieses Prinzip zur Ermittlung der Kreiszahl π grafisch veranschaulichen.

Eine Nadel der Länge 0 < a < 1 werde auf eine Ebene geworfen, auf welcher im Abstand von einer Längeneinheit horizontale Striche gezogen seien. Wie groß ist die Wahrscheinlichkeit, dass die Nadel eine Linie schneidet? Es stellt sich heraus, dass diese Wahrscheinlichkeit a/π beträgt. Somit kann π durch eine derartige Simulation näherungsweise bestimmt werden.

Im Formularbereich Einstellungen / Ergebnisse können Sie die Anzahl horizontal angeordneter Linien, sowie die Anzahl durchzuführender Würfe (Bedienelement mit der Beschriftung Faktor) vorgeben. Die Bedienung des Schalters Berechnen löst die Simulation dieser Würfe aus.

In den Anfangszustand versetzen können Sie dieses relativ ungenaue Experiment durch die Bedienung des Schalters Zurücksetzen.
 

 
Nach der Festlegung der Anzahl horizontal verlaufenden Linien auf 30 und der Einstellung des Faktors auf 1000, erhalten Sie nach 10-maligem Bedienen der Schaltfläche Berechnen folgende Ergebnisse:

Anzahl der Würfe: 10000

Anzahl der Schnitte: 6288
 

Die Kreiszahl π wird hierdurch näherungsweise mit dem Wert π = 3,180662 ermittelt.
 

 

 

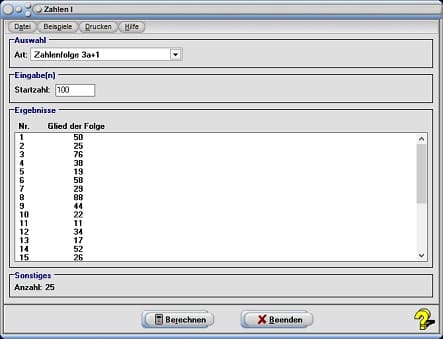
Eine Zahlenfolge natürlicher Zahlen, welche grundsätzlich periodisch mit den Werten 4, 2 und 1 endet, können Sie nach einer Wahl des Eintrags Zahlenfolge 3a+1 aus der aufklappbaren Auswahlbox untersuchen.
 

Ist das Startglied a(1) der Zahlenfolge eine beliebige natürliche Zahl und werden die Glieder der Zahlenfolge wie folgt definiert, so endet diese grundsätzlich mit den Zahlen 4, 2 und 1.

a_n+1 = a_n / 2 (wenn a_n gerade ist)

a_n+1 = 3·a_n + 1 (wenn a_n ungerade ist)
 

Nach der Eingabe des Startwerts in das entsprechende Feld Startzahl und einer Bedienung der Schaltfläche Berechnen werden die Ergebnisse ausgegeben.
 

 
Nach einer Festlegung der Startzahl auf 10, ermittelt das Programm:

Nr.	Glied der Folge
1	5
2	16
3	8
4	4
5	2
6	1

Bei einer Startzahl von 6 werden ausgegeben:

Nr.	Glied der Folge
1	3
2	10
3	5
4	16
5	8
6	4
7	2
8	1

Wie hierbei zu erkennen ist, besitzen die letzten drei Glieder dieser Folgen in beiden Fällen die Werte 4, 2 und 1.
 

 

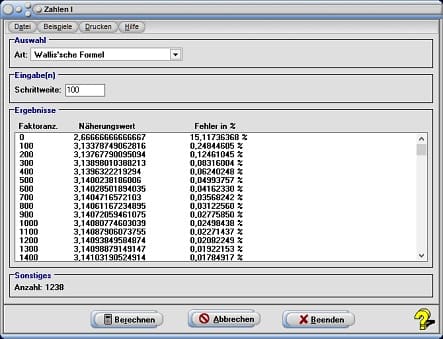
Eine Möglichkeit zur Ermittlung der Kreiszahl π durch die Bildung eines unendlichen Produkts wurde im 17. Jahrhundert vom englischen Mathematiker John Wallis entdeckt:
 

(2/1 · 2/3) · (4/3 · 4/5) · (6/5 · 6/7) · (8/7 · 8/9) ... = π/2

Die Genauigkeit dieses Verfahrens können Sie untersuchen, indem Sie den Eintrag Wallis'sche Formel aus der aufklappbaren Auswahlbox wählen und hierauf die Schaltfläche Berechnen bedienen. Das Programm führt die entsprechenden Berechnungen durch und gibt den ermittelten Wert für die Kreiszahl π nach jeweils 100 Schritten aus.

Die prozentuale Abweichung der Werte der Zwischenergebnisse zu einem sehr genauen Wert für π wird jeweils nach Durchführung der vorgegebenen Anzahl von Berechnungen angezeigt. Die u.U. lang andauernde Berechnung können Sie anhalten, indem Sie den Schalter Abbrechen bedienen.
  

 

 
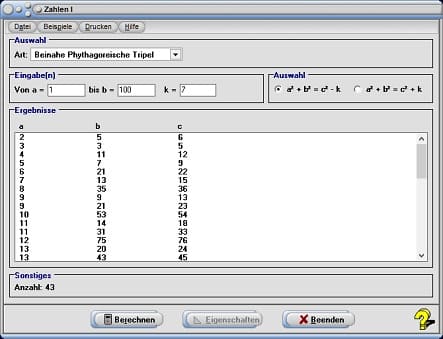
Wird der Eintrag Beinahe Pythagoreische Tripel gewählt, so kann nach Tripeln natürlicher Zahlen gesucht werden, für welche gilt:

 a² + b² = c² ± k

Möchten Sie die Untersuchung mit einem Wert für k durchführen für welchen k < 0 gilt, so aktivieren Sie den Kontrollschalter a² + b² = c² - k, soll k hingegen größer 0 sein, so wählen Sie den Kontrollschalter a² + b² = c² + k. Geben Sie hierauf den ganzzahligen Wert für k in das Feld mit der Bezeichnung k ein.

Nach der Festlegung des Untersuchungsbereichs, durch die Eingabe entsprechender Werte für die Koeffizienten a und b der Gleichung in die Felder von a und bis b, ermittelt das Programm die ganzzahligen Koeffizienten für a, b und c nachdem die Taste Berechnen bedient wurde.

Möchten Sie Details zu den Eigenschaften eines Dreiecks erfahren, welches die Seitenlängen a,b und c besitzt, so fokussieren Sie hierfür den entsprechenden Tabelleneintrag und bedienen hierauf die Schaltfläche Eigenschaften. Dreiecke dieser Art sind nahezu rechtwinklig. 
 

 
Über einen Wertebereich von a = 1 bis b = 12 und bei einer Festlegung des Parameterwerts k = 1 erhalten Sie für a² + b² = c² - k folgende Tripel:

a	b	c
2	2	3
4	8	9
12	12	17

Diese Werte für a, b und c erfüllen die Gleichungsbedingung:

a² + b² = c² - 1

Für die Eigenschaften des Phythagoreischen Dreiecks mit den Seitenlängen

a = 4
b = 8
c = 9

erhalten Sie zudem folgende Informationen:

Winkel α: 26,384°
Winkel β: 62,72°
Winkel γ: 90,895°

Seitenhalbierende sha = 8,276
Seitenhalbierende shb = 5,701
Seitenhalbierende shc = 4,444

Winkelhalbierende wha = 8,247
Winkelhalbierende whb = 4,729
Winkelhalbierende whc = 3,742

Höhe h_a = 7,999
Höhe h_b = 4
Höhe h_c = 3,555

Fläche: A = 15,998 FE
Umfang: U = 21
Inkreisradius: r_i = 1,524
Umkreisradius: r_u = 4,501
 

 

 

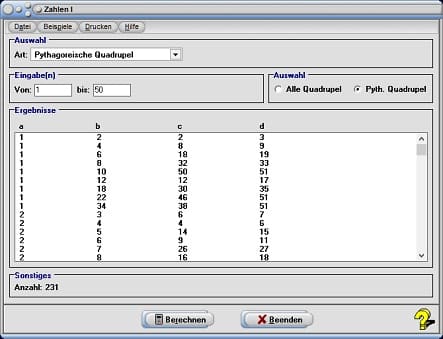
Pythagoreische Quadrupel sind die Quadrupel natürlicher Zahlen a, b, c und d, die die Bedingungen a² + b² + c² = d² und a ≥ b ≥ c ≥ d erfüllen. Diese können Sie ermitteln lassen, indem Sie den Eintrag Pythagoreische Quadrupel aus der aufklappbaren Auswahlbox wählen.

 

Wählen Sie durch die Aktivierung des entsprechenden Kontrollschalters Alle Quadrupel bzw. Pythagoreische Quadrupel, ob alle Quadrupel, oder lediglich Pythagoreische Quadrupel ermittelt werden sollen. Den Wertebereich für a, innerhalb dem nach Quadrupeln gesucht werden soll, bestimmen Sie durch die Eingabe der entsprechenden Werte in die Felder von und bis. Bedienen Sie die Schaltfläche Berechnen, so werden die entsprechenden Quadrupel in der Tabelle ausgegeben.
 

 

 
Nach der Festlegung eines Untersuchungsbereichs von 10 bis 14 zur Auffindung Pythagoreischer Quadrupel gibt das Programm folgende Ergebnisse für die Koeffizienten a, b, c und d der Gleichung aus:
 

a	b	c	d
12	12	14	22

 
Diese erfüllen die Bedingung: 12² + 12² + 14² = 22²
 

 

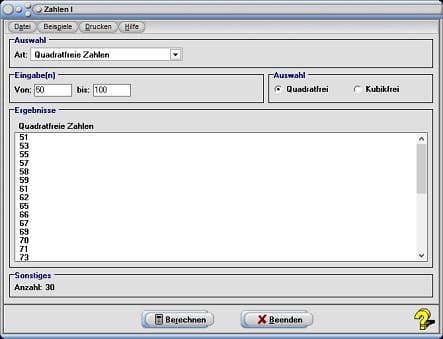
Eine quadratfreie, natürliche Zahl ist eine natürliche Zahl, die kein Vielfaches einer Quadratzahl > 1 ist. Es sind dies genau die Zahlen, welche sich als Produkt von paarweise verschiedenen Primzahlen schreiben lassen. Kubikfreie natürliche Zahlen sind natürliche Zahlen, die kein Vielfaches einer Kubikzahl > 1 sind. Diese Zahlen können Sie sich ausgeben lassen, nachdem Sie den entsprechenden Untersuchungsbereich durch Eingabe von Werten in die Felder Von und Bis festgelegt haben. Sollen quadratfreie Zahlen ermittelt werden, so aktivieren Sie den Kontrollschalter Quadratfrei, andernfalls den Kontrollschalter Kubikfrei und bedienen hierauf die Schaltfläche Berechnen.
 

 
Bei einer Suche nach quadratfreien Zahlen im Bereich von 1 bis 10 ermittelt das Programm:

1,2,3,5,6,7,10 ......

Bei der Suche kubikfreier Zahlen, innerhalb eines Bereichs von 1 bis 10, werden die Zahlen

1,2,3,4,5,6,7,9,10 ....

ausgegeben.
 

 

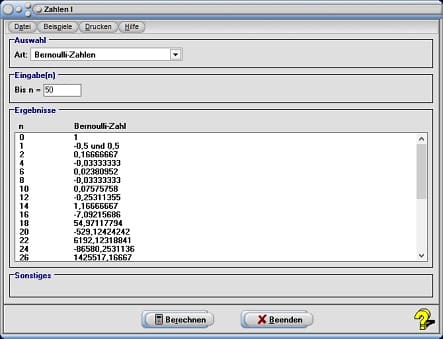
Die Bernoulli-Zahlen 1, ±1/2, 1/6, 0, -1/30, ... sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: In den Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler-Maclaurin-Formel und in der Zahlentheorie in Zusammenhang mit der Riemannschen Zetafunktion. Die Benennung dieser Zahlen nach ihrem Entdecker Jakob Bernoulli wurde von Abraham de Moivre eingeführt.

 

 

n   Bernoulli-Zahl

 

0    1

1    -0.5 und 0.5

2    0,1666666

4    -0,033333

6    0,02380952

8    -0,0333333

10   0,0757575

  

Liste aller natürlicher Zahlen von 1 bis 1000

 
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000
   

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden. Dieses Programm kann auch dabei behilflich sein, einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Zahlen II

 

 

Hinweis:

Da die Durchführung einiger Berechnungen sehr zeitaufwändig sein kann, können Sie diese jederzeit durch einmaliges Drücken der Taste ESC abbrechen.
 

 

Beispiel 1 - Buffonsches Nadelexperiment


Beispiel 2 - Leibniz-Formel

   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Heron-Verfahren
Wikipedia - Pythagoreisches Tripel
Wikipedia - Buffonsches Nadelproblem
Wikipedia - Leibniz-Formel
Wikipedia - Wallissches Produkt
Wikipedia - Quadratfreie Zahl
Wikipedia - Bernoulii-Zahl
 

 

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte

 

MathProf 5.0 - Unterprogramm Zahlen II

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---