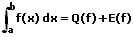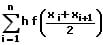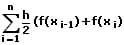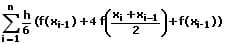MathProf - Trapezregel - Simpson-Verfahren - Näherungsverfahren

 

Modul Integrationsmethoden

---

 
Das Unterprogramm [Analysis] - [Integrationsverfahren] - Integrationsmethoden ermöglicht die Gegenüberstellung und Untersuchung verschiedener Integrationsmethoden.
 

Einleitung

 
Die numerische Mathematik (Numerik) ist ein Teilgebiet der Mathematik die sich mit der Bildung und Analyse mathematischer Probleme beschäftigt.

Als numerische Integration (numerische Quadratur oder numerisches Integrieren) wird die näherungsweise Berechnung von Integralen bezeichnet. In diesem Modul werden verschiedene numersiche Verfahren (Methoden bzw. numerische Methoden) einander gegenübergestellt mit Hilfe derer derartige Berechnungen durchgeführt werden können. Sie werden als Integrationsverfahren oder numerische Integrationsverfahren bezeichnet.
 
Bei der Durchführung einer numerischen Integration wird das Integral einer Funktion f über dem Intervall [a,b] dargestellt als die Summe aus dem Wert Q(f) einer Quadraturformel (Näherungsformel) sowie einem Fehlerwert E(f). Es gilt:



Die Mittelpunktsregel (auch als Rechteckregel, Rechteckverfahren, Tangentenregel, Trapezregel oder Trapezverfahren bzw. Sehnentrapezregel bezeichnet) ist ein numerisches Verfahren welches zur näherungsweisen Berechnung von Integralen verwendet wird.
 
Auch die Simpsonregel oder Simpsonsche Formel ist ein Verfahren dieser Art. Hierbei wird in einem Intervall ein Integral berechnet wird, indem die Funktion durch eine exakt integrierbare Parabel angenähert wird. Diese Methode wird auch  Simpson-Verfahren oder Simpson-Methode genannt. Zudem ist die 3/8-Regel (3/8-Methode) ein Verfahren zur Durchführung derartiger Berechnungen.

Die Gauß Integration (oder Gauß-Quadratur) ist ein Verfahren zur numerischen Berechnung von Integralen der Form ∫abΦ(x)w(x)dx mit optimaler Ordnung. Eine Newton-Cotes-Formel ist eine numerische Quadraturformel zur näherungsweisen Berechnung von Integralen. Die Trapezformel oder Sehnentrapezformel ermöglicht es gemäß der Gaußschen Trapezformel die Fläche eines einfachen Polygons zu berechnen.

Im Folgenden wird auf die in diesem Modul implementierten numerischen Näherungsverfahren zur Durchführung der Integralrechnung eingegangen.
 

Integrationsmethoden I

 
 

Die Wahl des Registerblatts Integrationsmethoden I ermöglicht den Vergleich folgender Methoden (numerische Integrationsverfahren) zur Ermittlung von Flächen unter Funktionen in expliziter Form:
 

• Simpson-Methode (Simpson-Formel, Simpson-Regel)
• Rechteck-Methode (Rechteck-Formel, Rechteck-Regel oder Mittelpunktsregel)
• Trapez-Methode (Trapez-Formel, Trapez-Regel)

 
Bei Anwendung der entsprechenden Näherungsverfahren werden in diesem Unterprogramm ausgegeben:
 

• Simpson-Methode (Simpson-Verfahren): Fläche zwischen Funktion und Abszisse, die durch die Verwendung des Simpson-Verfahrens bei vorgegebener Stützstellenanzahl ermittelt wird. 
• Rechteck-Methode (Rechteck-Verfahren bzw. Mittelpunktsregel): Fläche zwischen Funktion und Abszisse, die durch die Verwendung des Rechteck-Verfahrens bei vorgegebener Stützstellenanzahl ermittelt wird.
• Trapez-Methode (Trapez-Verfahren): Fläche zwischen Funktion und Abszisse, die durch die Verwendung des Trapez-Verfahrens bei vorgegebener Stützstellenanzahl ermittelt wird.
   
• Integral: Die absolute Fläche (Vergleichswert), die mittels einem genauen Verfahren und einer relativ hohen Stützstellenanzahl errechnet wird.

Die prozentualen Angaben des relativen Fehlers bei einzelnen Verfahren beziehen sich hierbei auf den mittels eines genauen Verfahrens errechneten Wert (Integral).

Nachfolgend aufgeführt sind die Formeln der in diesem Registerblatt zur Auswahl stehenden Integrationsmethoden. Es sind dies die summierte Mittelpunktsregel, die summierte Trapezregel sowie die summierte Simpsonregel.
 
Summierte Mittelpunktsregel:


 
Summierte Trapezregel:



Summierte Simpsonregel:



Bei allen zuvor aufgeführten Verfahren erfolgt hierbei die Zerlegung des festgelegten Intervalls [a,b] in jeweils n Teilintervalle [x_i−1, x_i] mit x₀ = a, x_i = a + ih, h = (b − a)/n und i = 1,2,3 ...n
 

 
Möchten Sie diese Verfahren der numerischen Integration einander gegenüberstellen, so gehen Sie wie folgt vor:
 

1. Aktivieren Sie das Registerblatt Integrationsmethoden I.
    
2. Definieren Sie die mathematische Funktion, mit welcher Sie Untersuchungen durchführen möchten, im Eingabefeld mit der Bezeichnung f(x) =.
    
3. Legen Sie die Intervallgrenzen fest, über welche die Integration durchgeführt werden soll (Bereich von x1 = und bis x2 =).
    
4. Bestimmen Sie die Anzahl zu verwendender Stützstellen durch eine Bedienung des Rollbalkens Anz. Stützstellen.
    
5. Wurde der Funktionsterm, gemäß den geltenden Syntaxregeln formuliert, so erfolgt die numerische Auswertung nach einer Bedienung der Schaltfläche Berechnen.
    
6. Möchten Sie sich Zusammenhänge grafisch veranschaulichen, so bedienen Sie die Schaltfläche Darstellen.
    
7. Wählen Sie auf dem Bedienformular durch die Aktivierung des Kontrollschalters Rechteck-Methode, Trapez-Methode oder Simpson-Methode aus, welches Verfahren benutzt werden soll.
    
8. Das Programm verwendet nach Aufruf der grafischen Darstellung für die zu verwendende Stützstellenanzahl den im Eingabefeld Anzahl Stützstellen festgelegten Wert. Durch eine Bedienung des Rollbalkens Anzahl Stützstellen kann dieser hierauf verändert werden.
    
9. Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

  

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Bei Ausgabe einer grafischen Darstellung bei Wahl des Registerblatts Integrationsmethoden I wird nachfolgend gezeigtes Bedienformular zur Verfügung gestellt.

 
Durch die Aktivierung der entsprechenden Kontrollschalters kann hierauf das anzuwendende Verfahren selektiert werden.
 

Integrationsmethoden II

 

 

Auf dem Registerblatt Integrationsmethoden II werden folgende Integrationsmethoden (Näherungsverfahren) zur Durchführung einer numerischen Analyse gegenübergestellt (Durchführung der numerischen Integration):
 

• Rechteckregel (Obersummen)
• Rechteckregel (Untersummen)
• Trapezregel (Trapez-Formel, Trapez-Methode, Trapezverfahren)
• Simpson-Verfahren (Simpson-Formel, Simson-Regel)
• 3/8-Regel
• 4. Newton-Cotes-Formel
• 5. Newton-Cotes-Formel
• 6. Newton-Cotes-Formel
• 7. Newton-Cotes-Formel
• Tschebychow-Verfahren
• Gauß-Quadratur

 
Es stehen zwei nebeneinander angeordnete, aufklappbare Boxen zur Verfügung, um Integrationsverfahren auszuwählen. Bei Auswahl der Gauß-Quadratur ist durch die Bedienung des dafür vorgesehenen Steuerelements die Anzahl zu verwendender Stützstellen (zw. 2 und 6) festzulegen. Es wird ermöglicht, Vergleiche zwischen den Verfahren bzgl. derer Methodik anzustellen. Die Berechnungen werden mit vorgegebenen Stützstellenanzahlen durchgeführt. Voraussetzung zur Nutzbarkeit dieser Methoden ist, dass die zu untersuchende Funktion im Bereich x₁ < x < x₂ definiert ist und keine Polstellen besitzt.

Die Simpsonregel benötigt eine ungerade Anzahl von Stützstellen. Bei der 3/8-Regel muss die Anzahl der zu verwendenden Stützstellen abzüglich 1 durch 3 teilbar sein. Alle, außer der Mittelpunktsregel, aufgeführten Methoden bedürfen einer Auswertung an den entsprechenden Intervallgrenzen. Die Mittelpunktregel erfordert eine derartige Auswertung je Intervall.
 

 

 

Um zwei dieser o.a. Verfahren zu vergleichen, gehen Sie folgendermaßen vor:
 

1. Aktivieren Sie das Registerblatt Integrationsmethoden II.
    
2. Definieren Sie die mathematische Funktion, mit welcher Sie Untersuchungen durchführen möchten, gemäß den geltenden Syntaxregeln im Eingabefeld mit der Bezeichnung f(x) =.
    
3. Wählen Sie zwei zu vergleichende Verfahren aus den aufklappbaren Auswahlboxen.
    
4. Legen Sie den Intervallbereich, über welchen das entsprechende Verfahren angewandt werden soll, durch die Eingabe von Werten in die entsprechenden Felder fest (Bereich von x1 = und bis x2 =).
    
5. Bedienen Sie die Schaltfläche Berechnen. Die errechneten Werte werden mitsamt der Angabe der hierfür verwendeten Anzahl von Stützstellen in den Tabellen ausgegeben.
    
6. Die Fläche die zwischen der Funktion und der Abszisse, innerhalb des vorgegebenen Intervallbereichs eingeschlossen wird, können Sie betrachten indem Sie die Schaltfläche Darstellen bedienen.

 

Nachfolgend aufgeführt sind Formeln zu einigen in diesem Unterprogramm unter Integrationsmethoden II zur Verfügung stehenden Integrationsverfahren.
 
1. Newton-Cotes-Verfahren:



mit:



h = (b - a)/n
a = x₀
b = x_n
 
p_in sind Gewichte und in nachf. gezeigter Tabelle aufgeführt:
 

n	Pn	p0n	p1n	p2n	p3n	p4n	p5n	p6n	p7n	Rn [f]
1	2	1	1							${\displaystyle -\frac{{\left(\frac{b-a}{2}\right)}^5}{90}{f}^{(4)}(\xi )}${\displaystyle -{\frac {\left({\frac {b-a}{2}}\right)^{5}}{90}}f^{(4)}(\xi )}
2	6	1	4	1
3	8	1	3	3	1
4	90	7	32	12	32	7				${\displaystyle -\frac{3{\left(\frac{b-a}{3}\right)}^5}{80}{f}^{(4)}(\xi )}${\displaystyle -{\frac {3\left({\frac {b-a}{3}}\right)^{5}}{80}}f^{(4)}(\xi )}
5	288	19	75	50	50	75	19
6	840	41	216	27	272	27	216	41
7	17820	751	3577	1323	2989	2989	1323	3577	751

 
mit x₀ < ζ < x_n


2. Sehnen-Trapezformel:



n: Anzahl gleicher Stufen


3. Simpsonsche Regel:



n: Anzahl gleicher Stufen - gerade


4. Newtonsche 3/8-Regel:




5. Rechteckregel:



n: Anzahl gleicher Stufen


6. Tangentenformel:



n: ungerade

7. Gauß-Quadratur:



w(x): Gewichtsfunktionen
R_n(f): Quadraturfehler
Knoten x_k sind nicht äquidistant

Gebräuchliche Gewichtsfunktionen sind:
 

[a,b]	w(x)
[-1,1]	1	Gauß-Legendre
[-1,1]	(1-x²)-1/2	Gauß-Tschebyscheff
[0,∞]	exp(-x)	Gauß-Laguerre
[-∞,∞]	exp(-x2)	Gauß-Hermite

 
   

 

 
Nach der Wahl des Registerblatts Integrationsmethoden II wird bei der Ausgabe einer grafischen Darstellung das nachfolgend gezeigte Bedienformular zur Verfügung gestellt, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist. Hierauf können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• Punkte beschriften: Darstellung der Mausfangpunkte ein-/ausschalten
• Koordinaten: Anzeige der Koordinaten der Mausfangpunkte ein-/ausschalten
• Bereichsmarkierung: Anzeige der Bereichsmarkierung ein-/ausschalten

 

 

In diesem Programmteil können ausschließlich Funktionen untersucht werden, die über den gewünschten Integrationsbereich stetig sind und innerhalb dieses Intervalls keinen negativen Funktionswert besitzen. Trifft dies nicht zu, so erhalten Sie eine Fehlermeldung.

Prüfen können Sie dies, indem Sie vor der Durchführung von Berechnungen das Kontrollkästchen Funktionsanalyse aktivieren und daraufhin die Schaltfläche Darstellen bedienen.

Die entsprechende Funktion wird dargestellt. Der gewählte Integrationsbereich wird markiert. Hieraus kann entnommen werden, ob die Funktion im gewählten Bereich negative Funktionswerte besitzt. Wählen Sie hierauf den Integrationsbereich derart, dass eine Berechnung nur über einen Bereich durchgeführt wird, innerhalb dessen die Funktion keine negativen Werte besitzt und veranlassen Sie die Durchführung der Berechnungen. Vor der erneuten Untersuchung eines Integrationsverfahrens ist dieses Kontrollkästchen wieder zu deaktivieren.

Eine Verwendung von Funktionsparametern (Zeichen P) ist nicht möglich.
 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Ober - und Untersummen

Ober - und Untersummen - Interaktiv

Integration

Integration - Interaktiv

 

 
Beispiel 1 - Integrationsmethoden I:

Die drei zur Verfügung stehenden Integrationsverfahren sollen am Beispiel der Funktion f(x) = sin(x) einander gegenübergestellt werden. Hierzu ist ein Integrationsbereich 0 ≤ x ≤ 3 festzulegen und die Berechnungen sind mit den Stützstellenanzahlen 4, 8, 10, 20 und 50 aufeinanderfolgend durchzuführen.

 

Vorgehensweise und Lösung:

 

Wählen Sie das Registerblatt Integrationsmethoden I, definieren Sie im Eingabefeld f(x) = den Term SIN(X) und geben Sie in die Felder Bereich (Intervallgrenzen) von x1 = und bis x2 = die Werte 0 und 3 ein. Positionieren Sie hierauf aufeinanderfolgend den Rollbalken Anz. Stützstellen auf die entsprechenden Werte für Stützstellenanzahlen und klicken Sie anschließend auf die Schaltfläche Berechnen.

 

Nach Durchführung der fünf Untersuchungen erhalten Sie folgende Ergebnisse:

 

Anzahl Stützstellen:	4	10	50
Simpson-Methode (Simpson-Formel):	1,9937	1,9900	1,9900
Rechteck-Methode (Rechteck-Formel):	1,8429	1,9539	1,9852
Trapez-Methode (Trapez-Formel):	1,8958	1,9750	1,9894

Da die exakte Fläche unter der Kurve in diesem Bereich 1,99 FE beträgt, kann entnommen werden, dass die Simpson-Methode die schnellste Konvergenz aufweist.
 

Beispiel 2 - Integrationsmethoden II:

Es gilt, die Integrationsverfahren Trapez-Regel und Simpson-Regel unter Verwendung der Funktion f(x) = cos(x)-x², für einen Untersuchungsbereich 0 ≤ x ≤ 2 einander gegenüberzustellen.

Vorgehensweise und Lösung:

Wählen Sie das Registerblatt Integrationsmethoden II.

Nach der Definition des Terms COS(X)-X^2 im Eingabefeld f(x) = und der Festlegung des Integrationsbereichs durch die Eingabe der Zahlenwerte 0 und 2 in die entsprechenden Felder Bereich (Intervallgrenzen) von x1 = und bis x2 =, erhalten Sie nach einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse:

Trapez-Verfahren:

Stützstellenanzahl	Wert
2	-2,167771
5	-1,822859
10	-1,773736
20	-1,761460
50	-1,758024
100	-1,757533
200	-1,757410
500	-1,757376
1000	-1,757371
2000	-1,757370

Simpson-Verfahren:

Stützstellenanzahl	Wert
4	-1,757044
10	-1,757361
20	-1,757369
50	-1,757369
100	-1,757369
200	-1,757369
500	-1,757369
1000	-1,757369
2000	-1,757369

Aufgrund der Tatsache, dass die exakte Fläche unter der Kurve in diesem Bereich ~1,757369 FE beträgt, kann auch hierbei geschlussfolgert werden, dass die Simpson-Methode die schnellste Konvergenz aufweist.

   

 

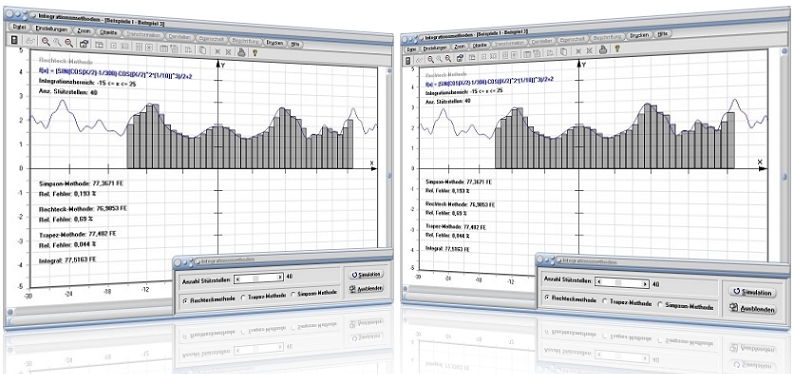
Grafische Darstellung - Beispiel 1
 

Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5
   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Trapezregel sowie unter Wikipedia - Trapezmethode und Wikipedia - Mittelpunktsregel zu finden.
 

 

 

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

 

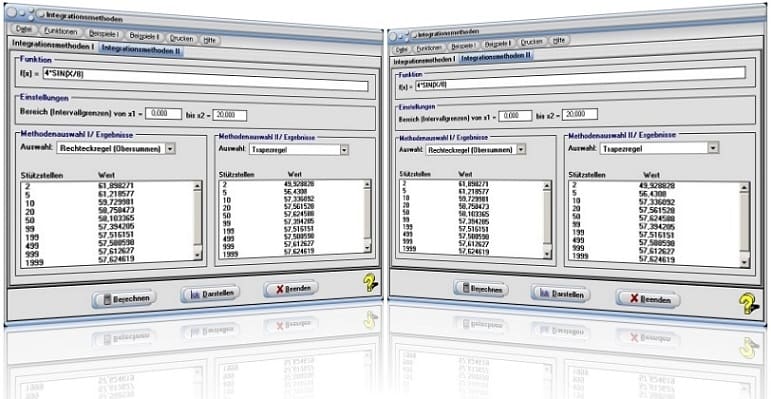
Startfenster des Unterprogramms Integrationsmethoden
 

MathProf 5.0 - Unterprogramm Integralrechnung - Interaktiv

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---