PhysProf - Strömung - Volumenstrom - Viskosität - Druck
Fachthemen: Ideale Strömung - Strömungslehre - Hydrodynamik
PhysProf - Mechanik - Ein Programm mit Formeln zur Physik wie auch zur Visualisierung physikalischer Sachverhalte aus der Naturwissenschaft mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.
Online-Hilfe für das Modul
zur Analyse und grafischen Simulation der Zusammenhänge, welche bei idealen Strömungen in Flüssigkeiten vorherrschen - Fachthema Strömungslehre.
Dieses Unterprogramm ermöglicht die Durchführung der Steuerung entsprechender Abläufe zur Echtzeit und bietet die Möglichkeit, die Einflüsse relevanter Größen interaktiv zu untersuchen. Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul: |
 |  |
Ideale Strömung
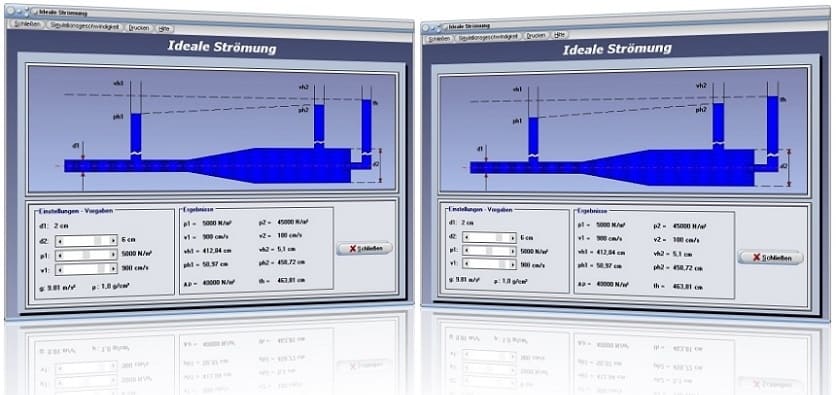
Modul Ideale Strömung
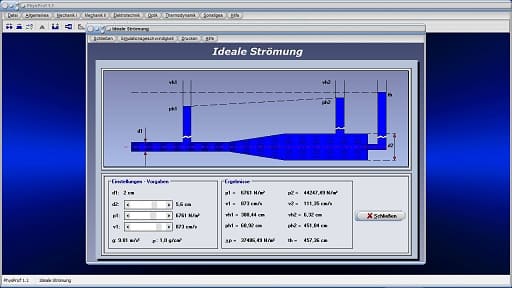
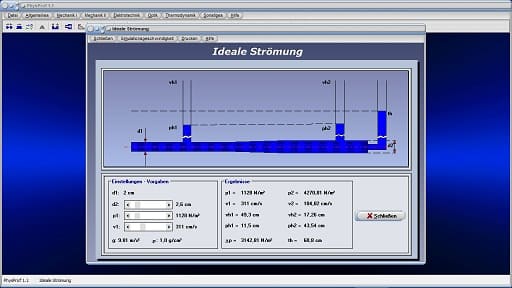
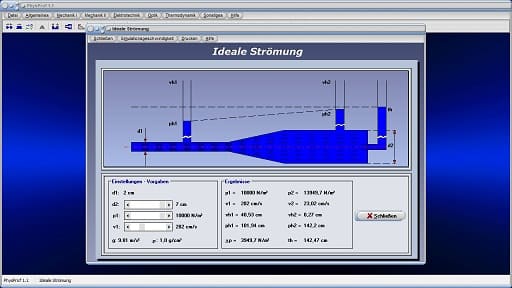
Das Unterprogramm [Mechanik I] - [Ideale Strömung] ermöglicht es, sich die Zusammenhänge, die bei einer idealen Strömung von Flüssigkeiten vorherrschen, am Beispiel des Venturi-Effekts zu verdeutlichen.
Ideale Strömung - Abbildung 1
Ideale Strömung - Abbildung 2
Ideale Strömung - Abbildung 3
Ideale Strömung - Abbildung 4
Als Strömungsmechanik (Fluidmechanik oder Strömungslehre) wird die Lehre des physikalischen Verhaltens von Fluiden bezeichnet. Strömungen sind Bewegungen von Flüssigkeiten oder Gasen. Ursache von Strömungen sind z.B. Schwerkraft und Druckdifferenzen. Von idealer Strömung spricht man, wenn von Wirbelbildungen und innerer Reibung abgesehen wird. Eine stationäre Strömung liegt vor, wenn der Druck, die Geschwindigkeit sowie die Eigenschaften des Fluids konstant sind und an jeder Stelle des Strömungsfelds zeitlich unabhängig sind.
Das Strömungsfeld beschreibt für jeden Punkt im Raum und zu jeder Zeit eine Geschwindigkeit, mit welcher physikalische Größen, wie beispielsweise Materialeigenschaften und Wirkungen von Kräften innerhalb eines räumlichen Bereichs transportiert werden. Trifft eines der zuvor aufgeführten Merkmale nicht zu, so wird von einem instationären Strömungszustand gesprochen und diese Strömung als instationäre Strömung bezeichnet.
Die Hydrodynamik ist ein Teilgebiet der Fluiddynamik und setzt sich mit der Strömungslehre für Flüssigkeiten auseinander. Die Fluiddynamik ist ein Themengebiet der Strömungslehre, die sich mit bewegten Flüssigkeiten und Gasen auseinandersetzt.
Grundlagen
Als Strömungsgeschwindigkeit (Fließgeschwindigkeit, mittlere Fließgeschwindigkeit oder Durchflussgeschwindigkeit) v wird die Geschwindigkeit einzelner Teilchen in einer strömenden Flüssigkeit bezeichnet. Sie wird meist in der Einheit m/s angegeben.
Der Volumenstrom (die Durchflussrate oder Durchflussmenge) ist eine physikalische Größe, die beschreibt, welches Volumen eines Mediums (Fluids) je Zeiteinheit durch einen festgelegten Querschnitt transportiert wird. Die SI-Einheit des Volumenstroms ist m³/s.
Der Massenstrom (Massendurchsatz) gibt die Masse eines Mediums (Fluids) an, die je Zeiteinheit einen festgelegten Querschnitt bewegt wird. Die SI-Einheit des Massenstroms ist kg/s.
Beim Durchfluss V durch Röhren gelten u.a. nachfolgend aufgeführte Gesetzmäßigkeiten:
V: Volumen der durch den Querschnitt A strömenden Flüssigkeit (Durchfluss) [m³]
A: Rohrquerschnitt [m²]
v: Strömungsgeschwindigkeit der Flüssigkeit [m/s]
t: Dauer der Strömung [s]
Der Volumenstrom (auch als Durchflussrate oder Durchflussmenge bezeichnet) Q ist wie folgt definiert:
Q: Volumenstrom [m³/s]
A: Rohrquerschnitt [m²]
V: Volumen der durch den Querschnitt A strömenden Flüssigkeit [m³]
t: Dauer der Strömung [s]
Die Größe m/t wird als Massenstrom bezeichnet. Für sie gilt:
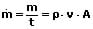
In differentieller Schreibweise:
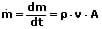
ṁ: Massenstrom [kg/s]
A: Rohrquerschnitt [m²]
v: Strömungsgeschwindigkeit der Flüssigkeit [m/s]
ρ: Dichte der Flüssigkeit [kg/m³]
Durchflussgesetz:
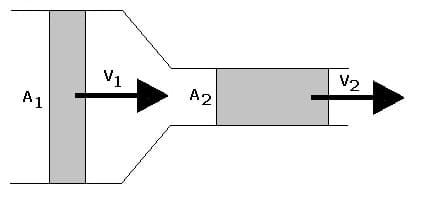
Das Durchflussgesetz (Kontinuitätsgesetz) lautet:
Es gilt: A ~ 1/v
A1: Querschnitt an Stelle 1 [m²]
A2: Querschnitt an Stelle 2 [m²]
v1: Geschwindigkeit an Stelle 1 [m/s]
v2: Geschwindigkeit an Stelle 2 [m/s]
Durch jeden Querschnitt eines Rohres tritt in der gleichen Zeit das gleiche Volumen, da Flüssigkeiten beinahe inkompressibel sind. Dies ist aus der o.a. Gleichung zu entnehmen. Ebenso kann hieraus gefolgert werden, dass die Fließgeschwindigkeit bei kleineren Querschnitten (bei einer Rohrverengung) höher ist als bei großen.
Drücke - Statischer Druck - Dynamischer Druck
In jeder Strömung setzt sich der Gesamtdruck aus zwei Teildrücken zusammen. Es sind dies:
-
der statische Druck:
folgt aus der potentiellen Energie der unter Druck stehenden Flüssigkeit
-
der dynamische Druck:
folgt aus der kinetischen Energie der strömenden Flüssigkeit
Gemäß dem Gesetz von Bernoulli gilt: In einer stationären Strömung ist die Summe aus statischem und dynamischen Druck konstant. Diese entspricht dem hydrostatischen Druck der ruhenden Flüssigkeit.
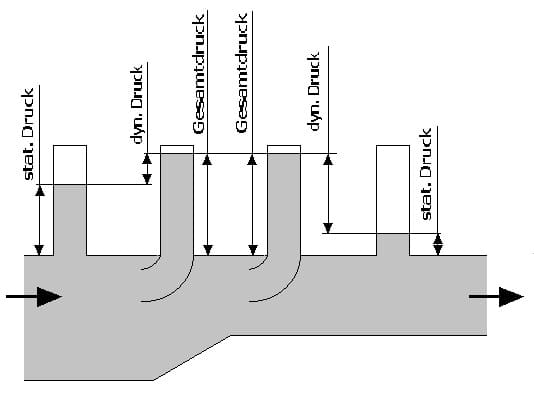
Mit wachsender Strömungsgeschwindigkeit wächst der dynamische Druck und es sinkt der statische Druck.
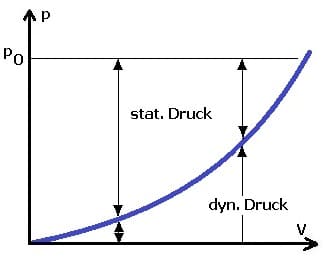
Verläuft eine Strömung in gleicher Höhe, so gilt:
Aus dieser Gesetzmäßigkeit (Bernoulli-Gleichung) lässt sich die Differenz zweier statischer Drücke ermitteln:
und mit Hilfe der Kontinuitätsgleichung:
lässt sich die Strömungsgeschwindigkeit v1 bestimmen, wenn die Strömungsgeschwindigkeit v2 bekannt ist:
Zudem gilt, dass jede Flüssigkeit infolge ihrer Gewichtskraft einen Schweredruck besitzt. Als Schweredruck (geodätischer Druck) wird der Druck bezeichnet, den ein Körper auf Grund der Gewichtskraft (Gravitation) der über ihm ruhenden Gas- oder Flüssigkeitssäule erfährt. Dieser kann wie folgt berechnet werden:
Hieraus lässt sich die Höhe der Strömung th ermitteln. Da an jeder Stelle des Rohres gilt
th = vh + ph
können unter Zuhilfenahme des o.a. Zusammenhangs alle statischen und dynamischen Drücke an jeder Stelle des Rohres ermittelt werden.
A1: Querschnitt an Stelle 1 [m²]
A2: Querschnitt an Stelle 2 [m²]
p1: Statischer Druck an Stelle 1 [Pa]
p2: Statischer Druck an Stelle 2 [Pa]
v1: Strömungsgeschwindigkeit an Stelle 1 [m/s]
v2: Strömungsgeschwindigkeit an Stelle 2 [m/s]
th: Gesamthöhe der Strömung [m]
vh: Höhe der Strömung durch dynamischen Druck [m]
ph: Höhe der Strömung durch statischen Druck [m]
Δp: Druckdifferenz p2 - p1 [Pa]
p: Schweredruck in der Tiefe h [Pa]
ρ: Dichte der Flüssigkeit [kg/m³]
h: Höhe der drückenden Flüssigkeitssäule [m]
Dieses Prinzip wird insbesondere zur Ermittlung der Strömungsgeschwindigkeit in Flüssigkeiten verwendet. Es wird hierdurch ermöglicht, an zwei verschiedenen Stellen eines Rohres mit unterschiedlichen Querschnitten, die Differenz der statischen Drücke zu messen und somit die Strömungsgeschwindigkeit bestimmbar zu machen.
Als Differenzdruck Δp wird der Druckunterschied bezeichnet, der zwischen zwei unterschiedlichen Druckmesspunkten besteht. Für ihn gilt:
Δp = p2 - p1
Δp: Differenzdruck [Pa]
p1: Druck an Stelle 1 [Pa]
p2: Druck an Stelle 2 [Pa]
Als hydrostatischer Druck wird derjenige Druck bezeichnet, der sich innerhalb einer ruhenden Flüssigkeit unter dem Einfluss der Schwerebeschleunigung oder Trägheit einstellt.
Als Wasserdruck wird der hydrostatische Druck bezeichnet, der innerhalb des Wassers herrscht. Dieser Druck steigt bei zunehmender Wassertiefe. Als Wassersäule wird eine nicht SI-genormte Einheit zur Messung dieses Drucks bezeichnet. Ein Meter Wassersäule (mWS) entspricht 9,80665 kPa (≈ 0,1 bar).
Programmbedienung
Zusammenhänge dieser Art können Sie sich verdeutlichen, wenn Sie die zur Verfügung stehenden Rollbalken bedienen. Das Programm visualisiert hierbei eine Strömungssimulation.
Zugrundegelegt wird, dass die Dichte der strömenden Flüssigkeit ρ = 1 g/cm³ beträgt. Der Durchmesser d1 des dargestellten Rohres (linksseitig) ist mit d = 2 cm vorgegeben. Den Durchmesser d2 des Rohres (rechtsseitig) können Sie durch eine Positionierung des Rollbalkens d2 verändern. Mittels der Bedienung der Rollbalken p1 und v1 verändern Sie den im linksseitig abgebildeten Rohrstück vorherrschenden Druck p1 sowie die dortige Fließgeschwindigkeit v1.
Neben der Anzeige der in den entsprechenden Rohrabschnitten vorherrschenden Drücke p1 und p2 erteilt das Programm Auskunft über die Strömungsgeschwindigkeiten v1 und v2. Zudem werden die Werte der durch den dynamischen Druck der Strömung verursachten Höhen vh1 und vh2 sowie die durch statischen Druck vorhandenen Höhen ph1 und ph2 ausgegeben. Auch wird der Wert für die Gesamthöhe th der Strömung angezeigt. Der Wert für Δp gibt Auskunft über die zwischen den beiden Rohrteilen vorherrschende Druckdifferenz.
Bernoullische Gleichung
Die Bernoulli-Gleichung (Bernoullische Gleichung) besagt, dass die spezifische Gesamtenergie von Teilchen auf dem Weg durch eine Strömungsröhre konstant bleibt. Hierbei verändern sich zwar die Anteile aus kinetischer, potentieller und Druckenergie, die Summe derer bleibt jedoch konstant.
Die Summe aus Staudruck, Schweredruck und statischem Druck wird als Gesamtdruck bezeichnet.
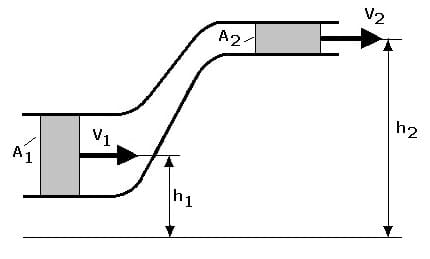
Die Bernoulli-Gleichung lautet:
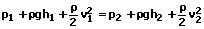
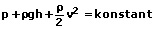
Wenn die Strömung in (annähernd) gleicher Höhe verläuft, so gilt:
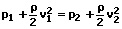
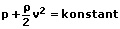
A1: Querschnitt an Stelle 1 [m²]
A2: Querschnitt an Stelle 2 [m²]
p1: Statischer Druck an Stelle 1 [Pa]
p2: Statischer Druck an Stelle 2 [Pa]
v1: Strömungsgeschwindigkeit an Stelle 1 [m/s]
v2: Strömungsgeschwindigkeit an Stelle 2 [m/s]
h1: Höhe der Strömung an Stelle 1 [m]
h2: Höhe der Strömung an Stelle 2 [m]
ρ: Dichte der Flüssigkeit [kg/m³]
Druckmessung
Bei jeder Art einer Strömung treten zwei verschiedene Arten von Drücken auf. Es sind dies der statische Druck sowie der dynamische Druck (Staudruck). Der dynamische Druck resultiert aus der Bewegungsenergie (Ekin) des strömenden Mediums. Der statische Druck beruht auf der Lageenergie (Epot) des unter Druck stehenden Mediums (Gas oder Flüssigkeit). Die Summe dieser beiden Drücke wird als Gesamtdruck p0 bezeichnet.
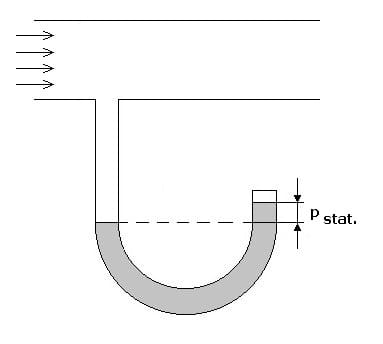
Abb.1 - Statischer Druck
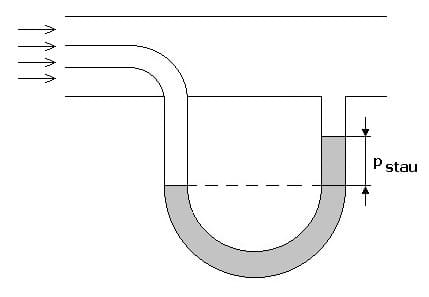
Abb.2 - Staudruck
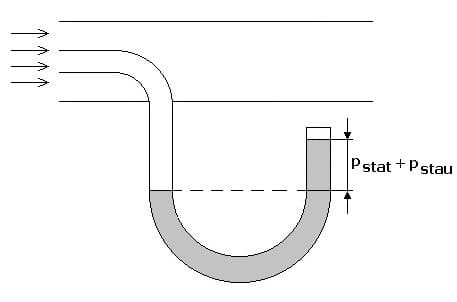
Abb.3 - Gesamtdruck
Die Messung dieser Drücke erfolgt durch unterschiedliche Verfahren. Der statische Druck wird durch ein zur Strömungsrichtung rechtwinklig positioniertes Manometer gemessen. Der Gesamtdruck wird mit einem Pilot-Rohr erfasst. Durch das in Strömungsrichtung angebrachte Rohr wird sowohl der statische wie auch der dynamische Druck erfasst. Da das durch das Rohr strömende Medium bei dessen Eintritt gebremst wird, wandelt sich der dynamische Druck in einen Staudruck, welcher gemessen werden kann.
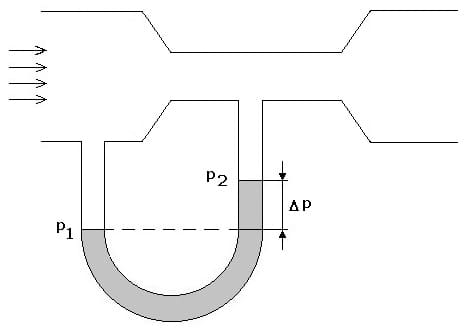
Die Differenz zweier statischer Drücke kann auch mit Hilfe des Venturi-Rohrs erfasst werden. Dieses ermöglicht insbesondere die Bestimmung der Strömungsgeschwindigkeit eines Mediums. Hierbei wird an zwei Stellen unterschiedlichen Querschnitts der dort jeweils vorhandene statische Druck erfasst. Aus der Differenz dieser beiden Drücke ist die Strömungsgeschwindigkeit bestimmbar. Als Bernoulli-Effekt (Venturi-Effekt) wird die Abnahme des statischen Drucks in strömenden Fluiden mit zunehmender Strömungsgeschwindigkeit bezeichnet.
Hierbei gilt für die Strömungsgeschwindkeit an Stelle 1:
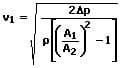
Der Volumenstrom der dort vorhandenen Strömung kann wie folgt ermittelt werden:
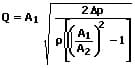
A1: Querschnitt an Stelle 1 [m²]
A2: Querschnitt an Stelle 2 [m²]
v1: Geschwindigkeit an Stelle 1 [m/s]
Q: Volumenstrom [m³/s]
ρ: Dichte des Mediums [kg/m³]
p1: Druck an Stelle 1 [Pa]
p2: Druck an Stelle 2 [Pa]
Δp: Druckdifferenz p2 - p1 [Pa]
Insbesondere zur Bestimmung der Strömungsgeschwindigkeit in Gasen wird das Prandtlsches Staurohr (Prandtlsonde) eingesetzt. Für diesen Fall gilt:
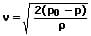
v: Geschwindigkeit des strömenden Mediums [m/s]
p0: Gesamtdruck [Pa]
p: Statischer Druck [Pa]
ρ: Dichte des Mediums [kg/m³]
Als Druckenergie wird die von einem Fluid verrichtete Arbeit bezeichnet, wenn dieses bei einem konstanten Druck sein Volumen erhöht. Sie entspricht der mechanischen Energie, die von einem unter Druck stehenden Fluid (Flüssigkeit oder Gas) befördert wird.
Dynamische Viskosität - Kinematische Viskosität - Zähigkeit
1. Dynamische Viskosität:
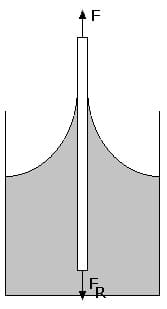
Mit der dynamischen Viskosität (auch als dynamische Zähigkeit bezeichnet) wird die Zähigkeit (Zähflüssigkeit) einer Flüssigkeit (eines Fluids) beschrieben. Je höher ihr Wert ist, desto zähflüssiger ist sie. Ein Fluid besitzt eine innere Reibung die zu überwinden ist, wenn sie auf einer ebenen Fläche bewegt werden soll. Sie ist dem Betrag nach identisch mit der Reibungskraft. Bei Flüssigkeiten nimmt die dynamische Viskosität mit zunehmender Temperatur stark ab, bei Gasen hingegen nimmt sie zu.
Es gilt:
η = FR·d(A·v)
η: Dynamische Viskosität [Ns/m²]
FR: Reibungskraft [N]
A: Berührfläche [m²]
v: Relative Geschwindigkeit zwischen zwei Berührflächen [m/s]
d: Abstand der beiden Berührflächen [m]
Wird die oberste Schicht mit der Geschwindigkeit v bewegt, so bewegt sich die direkt unterhalb dieser befindende Schicht auf Grund der Haftung ebenfalls mit dieser Geschwindigkeit v. Es gilt:
Δη = FR·Δd(A·v)
Δη: Dynamische Viskosität [Ns/m²]
v: Relative Geschwindigkeit zwischen zwei Berührflächen [m/s]
FR: Reibungskraft [N]
A: Berührfläche [m²]
Δd: Abstand der beiden Berührflächen [m]
Als viskose Reibung wird diejenige Reibung bezeichnet, die bei der Bewegung eines Körpers in einem Fluid (Flüssigkeit oder Gas) auftritt. Für den Fall, dass es sich beim Körper um eine Kugel handelt, gilt für sie:
FV = 6·π·r·v·η
FV: Viskose Reibungskraft [N]
η: Dynamische Viskosität der Flüssigkeit [Ns/m²]
r: Radius der Kugel [m]
v: Geschwindigkeit der Kugel [m/s]
2. Kinematische Viskosität - Reibungsgesetz:
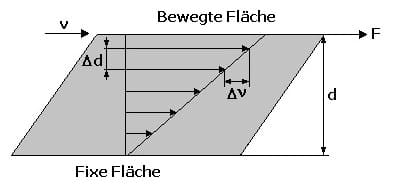
Als kinematische Viskosität wird das Verhältnis der dynamischen Viskosität und der Dichte eines Mediums bezeichnet. Für sie gilt:
ν = η/ρ
ν: Kinematische Viskosität [m²/s]
η: Dynamische Viskosität [Ns/m²]
ρ: Dichte [kg/m³]
Das Newtonsche Reibungsgesetz oder Reibungsgesetz beschreibt die Reibungskraft Fr für eine Platte, die mit gleichförmiger Geschwindigkeit über ein Fluid gezogen wird. Es gilt:
Fr = A⋅η⋅dv dy
Dabei gilt: A ist diejenige Fläche mit der der Körper auf dem Fluid liegt.
η: Dynamische Viskosität [Ns/m²]
Fr: Reibungskraft [N]
A: Berührfläche [m²]
Ausflussgeschwindigkeit
Als Ausflussgeschwindigkeit (Ausströmgeschwindigkeit oder Ausfließgeschwindigkeit) wird die Geschwindigkeit bezeichnet, mit welcher ein flüssiges Medium (Flüssigkeit oder Gas) von geringer Viskosität aus der Öffnung eines dieses beinhaltenden Gefäßes strömt. Sie hängt von der Höhe h der drückenden Flüssigkeitssäule ab.
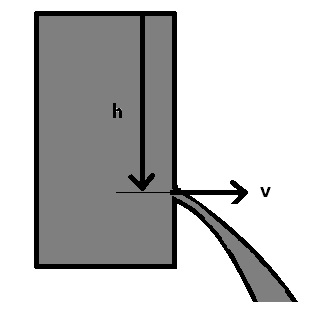
Für sie gilt:
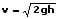
Diese Gleichung wurde nach dem italienischen Physiker und Mathematiker Evangelista Torricelli benannt.
v: Ausfließgeschwindigkeit [m/s]
h: Abstand der Ausflussöffnung vom Flüssigkeitsspiegel [m]
g: Fallbeschleunigung 9,81 m/s²
Der Ausflussbeiwert (Ausflusszahl) berücksichtigt die Verringerung der Ausflussgeschwindigkeit aufgrund der Viskosität der ausströmenden Flüssigkeit. Er hängt unter anderem davon ab, ob es sich um eine laminare oder turbulente Strömung handelt.
Wird dieser berücksichtigt, so gilt für die Ausflussgeschwindigkeit:
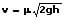
μ: Ausflussbeiwert
Nachfolgend aufgeführt sind die Zahlenwerte der Ausflussbeiwerte einiger Öffnungen.
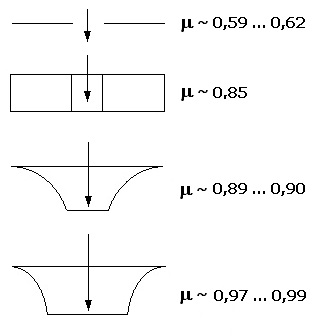
Unter einer laminaren Strömung (Laminarströmung) wird die Bewegung von Flüssigkeiten und Gasen verstanden, bei welcher keine erkennbaren Turbulenzen (Verwirbelungen) auftreten. Bei einer Rohrströmung besitzen einzelne Schichten des sich in einem Rohr bewegenden Mediums unterschiedliche Geschwindigkeiten. Bei Strömungen dieser Art handelt es sich meist um stationäre Strömungen. Von einer stationären Strömung wird gesprochen, wenn sich die vektorielle Strömungsgeschwindigkeit an den unterschiedlichen Orten im Rohr zeitlich nicht verändert.
Steigt die Geschwindigkeit der Bewegung eines Fluids, so tritt ab einer bestimmten Geschwindigkeit eine Veränderung im Strömungsprofil auf, welches sich durch Verwirbelungen bemerkbar macht. Als kritische Geschwindigkeit wird die Geschwindigkeit bezeichnet, oberhalb derer bei einer strömenden Flüssigkeit oder einem strömenden Gas die laminare (geordnete) Strömung in eine turbulente Strömung (wirbelnde Strömung) übergeht. Der bei einer turbulenten Strömung auftretende Druckverlust eines durch ein Rohr strömenden Fluids ist größer als derjenige, welcher bei einer laminaren Strömung auftritt.
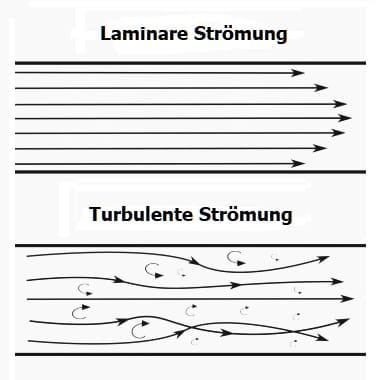
Unter einer Turbulenz bei Fluiden wird derer Strömungszustand und somit deren chaotische Bewegung verstanden, der/die sich durch eine wirbelnde Vermischung ihrer Bestandteile ergibt. Sie trägt in diesem Fall die Bezeichnung turbulente Strömung. Als laminare Strömung (Laminarströmung) wird die Bewegung von Gasen und Flüssigkeiten bezeichnet, bei der innerhalb einer Übergangsregion zwischen zwei verschiedenen Strömungsgeschwindigkeiten keine sichtbaren Verwirbelungen (Turbulenzen) auftreten. Unter den Strömungsarten wird im Wesentlichen zwischen laminarer und turbulenter Strömung unterschieden. Nachfolgend wird auf einige wichtige Größen der Strömungsberechnung eingegangen.
Reynoldssche Zahl:
Zur Berechnung des Strömungswiderstands bzw. der Strömungsleistung bei einer turbulenten Strömung wird ein Widerstandsbeiwert verwendet, der abhängig von der Form des umströmten Gebildes ist sowie dem Medium aus welchem dieses besteht. Dieser ist eine Funktion der Reynoldsschen Zahl (Re Zahl).
Diese Zahl wird unter anderem dazu verwendet, um die Art der vorliegenden Strömung zu bestimmen. Besitzt diese dimensionslose Kenngröße einen kleinen Wert, so liegt eine laminare Strömung vor, andernfalls handelt es sich um eine turbulente Strömung.
Bei der Erhöhung einer Strömungsgeschwindigkeit wird u. U. die kritische Geschwindigkeit vkrit erreicht, bei welcher sich die laminare Strömung in eine turbulente Strömung umwandelt. Der Wert der zur Bemessung der Art der Strömung (laminar oder turbulent) dient, wird als kritische Reynoldszahl RKrit bezeichnet: Bei Re > Rkrit. kann davon ausgegangen werden, dass eine turbulente Strömung vorliegt.
Besitzen zwei ähnliche Gebilde ähnliche Reynoldssche Zahlen, so verfügen sie auch über ähnliche Widerstandsbeiwerte und deren Strömungen sind einander ähnlich.
Die Reynoldssche Zahl ist wie folgt definiert:
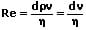
Re: Reynoldssche Zahl
d: Charakteristische Länge des Körpers (z.B. Radius des Rohres, der Kugel) [m]
η: Dynamische Viskosität [Ns/m²]
ν: Kinematische Viskosität [m²/s]
ρ: Dichte des strömenden Fluids [kg/m³]
v: Fließgeschwindigkeit zwischen Fluid und Körper [m/s]
Strömungswiderstand:
Der Strömungswiderstand (die Strömungswiderstandskraft FW) eines Körpers hängt von der Strömungsgeschwindigkeit zwischen Körper und Medium v, der Dichte ρ, der Viskosität η des Mediums (Fluids) sowie der Form des durchflossenen Körpers ab. Es gilt:
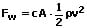
c: Widerstandsbeiwert
A: Widerstandsfläche [m²]
FW: Strömungswiderstand (Strömungswiderstandskraft) [N]
ρ: Dichte des strömenden Fluids [kg/m³]
v: Fließgeschwindigkeit zwischen Fluid und Körper [m/s]
Dynamischer Auftrieb:
Als dynamischer Auftrieb wird der Anteil der auf einen umströmten Körper wirkenden Kraft bezeichnet, der vertikal zur Anströmrichtung steht. Er wird durch Bewegung erzeugt und bildet sich beim Umströmen von Körpern, wenn die ihn umgebende, verdrängte und bewegte Luft nach unten beschleunigt wird.
Hydraulischer Durchmesser:
Zur Berechnung des Druckverlustes (und Durchsatzes) in Rohren deren Form von der Kreisform abweicht, kann der hydraulische Durchmesser als Näherungswert verwendet werden. Dieser berechnet sich wie folgt:
dh = 4·A/P
dh: hydraulischer Durchmesser [m]
A: Querschnittsfläche des Rohres [m2]
P: benetzter Umfang des Rohres [m]
Durchflusszahl:
Als Durchflusszahl (Lieferzahl) φ wird eine dimensionslose Kennzahl zur Beschreibung des Volumenstroms (Durchsatzes) bei Strömungsmaschinen bezeichnet. Sie bezieht sich auf die Fläche des Laufrades und seine Umfangsgeschwindigkeit und kann wie folgt bestimmt werden:
φ = 4V/(u·π2·D3)
φ: Durchflusszahl
D: Außendurchmesser des Laufrads [m]
V: Volumenstrom [m³/s]
u: Umfangsgeschwindigkeit [m/s]
Druckverlust:
Der Druckabfall (Druckverlust) beschreibt die Verminderung des Druckes in Strömungen. Durch die Beschleunigung der Teilchen eines Fluids wird ein ein statischer Druckabfall erzeugt.
Der Druckverlustbeiwert (Verlustbeiwert oder Widerstandsbeiwert) Zeta ist ein Maß für den in einem durchströmten Bauteil (einer Rohrleitung) entstehenden Druckverlust. Er beschreibt die Druckdifferenz die zwischen der Zuströmung und der Abströmung des Bauteils vorliegen muss, um einen vorgegebenen Durchfluss durch dieses aufrechtzuerhalten. Er ist unter anderem von der Reynolds-Zahl abhängig. Für ihn gilt:
ζ = 2·Δp/(ρ·v2)
ζ: Druckverlustbeiwert
ρ: Dichte des strömenden Fluids [kg/m³]
Δp: Druckverlust [Pa]
v: Geschwindigkeit des strömenden Fluids [m/s]
Mit dem Begriff Rohrreibung werden Reibungsverluste bezeichnet, die sich innerhalb einer Rohrleitung bilden. Reibung dieser Art entsteht an den Innenwänden des Rohres, an denen ein Medium entlangströmt.
Bei der Rohrreibungszahl λ handelt es sich um eine dimensionslose Kennzahl, die zur Berechnung des Druckabfalls einer Strömung aufgrund des in einem geraden Rohr vorhandenen Strömungswiderstands verwendet wird. Sie ist in erheblichem Maße abhängig von der Rauhigkeit der Rohroberfläche sowie von der Reynolds-Zahl. Für sie gilt:
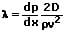
λ: Rohrreibungszahl
dp/dx: Druckgradient im Rohr
D: Durchmesser des Rohrs [m]
v: Mittlere Strömungsgeschwindigkeit [m/s]
ρ: Dichte des Mediums [kg/dm³]
Widerstandsbeiwert
In der folgenden Tabelle sind die Widerstandsbeiwerte c einiger Objekte aufgeführt.
| c | |
| Kugel | 0,1 - 0,4 |
| Stromlininenförmiger Körper | 0,05 |
| Zylinder (kreisförmig) bei Strömung quer zur Längsachse | 0,6 - 1,0 |
| Zylinder (kreisförmig) bei Strömung senkrecht zur Stirnfläche | 0,9 - 1,0 |
| Offener PKW | ≈ 0,9 |
| Geschlossener PKW | ≈ 0,4 |
| LKW | ≈ 0,9 |
| Rennwagen | ≈ 0,12 - 0,2 |
| Halbkugel (geöffnet) Öffnung gegen Strömung | 1,33 |
| Halbkugel (geöffnet) Abrundung gegen Strömung | 0,35 |
Nachfolgend sind die Werte der dynamischen Viskosität einiger Flüssigkeiten aufgeführt. Wenn nicht anders angegeben, so beziehen sich diese Angaben auf eine Temperatur von 20° C.
| Flüssigkeit | Dynamische Viskosität η in [mPa·s] |
| Aceton | 0,322 |
| Ameisensäure | 1,78 |
| Anilin | 4,4 |
| Asphalt | ≈ 1011 ... 1016 |
| Benzol (25 °C) | 0,601 |
| Bitumen | ≈ 107 ... 1014 |
| Blut (37 °C) | 3 ... 25 |
| Chloroform | 0,56 |
| Decan | 0,92 |
| Dioxan | 1,26 |
| Dodecan | 1,52 |
| Diethylether | 0,33 |
| Essigsäure (80%ig, 25 °C) | 2,31 |
| Ethanol | 1,19 |
| Ethylenglycol | 20,82 |
| Glas (flüssig) | ≈ 1022 ... 1024 |
| Glycerin (rein) | 1480 |
| Heptan | 0,41 |
| Hexan | 0,32 |
| Honig | ≈ 10000 |
| Kaffeesahne | ≈ 10 |
| Lack | ≈ 100 |
| Motoröl (25 °C) | ≈ 100 |
| Motoröl (150 °C) | ≈ 3 |
| Nonan | 0,711 |
| Octan | 0,538 |
| Olivenöl | ≈ 100 |
| Paraffinöl | ≈ 102 ... 106 |
| Pentan (25 °C) | 0,224 |
| Petroleum | 0,65 |
| Quecksilber | 1,55 |
| Rizinusöl | 990 |
| Sirup | ≈ 104 ... 105 |
| Steinsalz | ≈ 1018 ... 1021 |
| Toluol | 0,585 |
| Traubensaft | 2 ... 5 |
| Wasser (5 °C) | 1,52 |
| Wasser (20 °C) | 1,00 |
| Wasser (25 °C) | 0,891 |
In der folgenden Tabelle sind die Werte der dynamischen Viskosität einiger Gase aufgeführt. Diese Angaben beziehen sich auf eine Temperatur von 0° C bei 101,3 KPa.
| Gas | Dynamische Viskosität η in [μPa·s] |
| Acetylen | 9,5 |
| Ammoniak | 9,2 |
| Argon | 21,0 |
| Chlor | 12,3 |
| Chlormethan | 10,5 |
| Deuterium | 12,3 |
| Ethan | 8,6 |
| Ethylamin | 7,7 |
| Ethylen | 9,4 |
| Fluor | 21,9 |
| Formaldehyd | 11,4 |
| Helium | 18,6 |
| Kohlendioxid | 13,8 |
| Kohlenmonoxid | 16,6 |
| Luft | 18,2 |
| Methan | 10,2 |
| Neon | 29,7 |
| Propan | 7,5 |
| Propen | 8,3 |
| Sauerstoff | 19,2 |
| Schwefeldioxid | 12,3 |
| Stickstoff | 16,6 |
| Wasserstoff | 8,4 |
| Xenon | 21,1 |
Im Folgenden sind die Werte der kinematischen Viskosität einiger Flüssigkeiten aufgeführt. Diese Angaben beziehen sich auf eine Temperatur von 20° C.
| Flüssigkeit | Kinematische Viskosität ν in [mm²/s] |
| Aceton | 0,407 |
| Anilin | 4,31 |
| Benzol | 0,735 |
| Chloroform | 0,38 |
| Essigsäure (80%ig) | 1,16 |
| Ethanol | 1,51 |
| Glycerin (rein) | 1170 |
| Heptan | 0,595 |
| Olivenöl | 89 |
| Pentan | 0,37 |
| Quecksilber | 0,116 |
| Rizinulsöl | 1040 |
| Toluol | 0,677 |
| Wasser | 1,004 |
Im Folgenden sind die Werte der kinematischen Viskosität einiger Gase aufgeführt. Diese Angaben beziehen sich auf eine Temperatur von 0° C bei 101,3 KPa.
| Gas | Kinematische Viskosität ν in [mm²/s] |
| Acetylen | 8,1 |
| Ammoniak | 12,1 |
| Argon | 11,8 |
| Chlor | 3,82 |
| Ethan | 6,35 |
| Ethylen | 7,47 |
| Helium | 106 |
| Kohlendioxid | 6,93 |
| Kohlenmonoxid | 13,3 |
| Luft | 13,3 |
| Methan | 14,2 |
| Neon | 23,2 |
| Propan | 3,7 |
| Sauerstoff | 13,4 |
| Stickstoff | 13,2 |
| Wasserstoff | 93,8 |
| Xenon | 3,57 |
Ideale Strömung - Abbildung 5
Ideale Strömung - Abbildung 6
Ideale Strömung - Abbildung 7
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Hydrostatischer Druck sowie unter Wikipedia - Volumenstrom zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
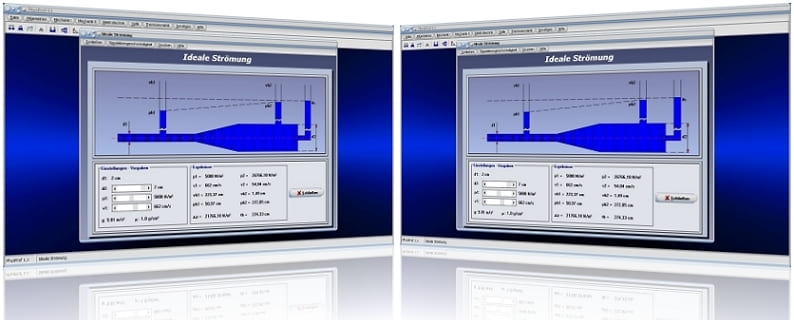
Unterprogramm Ideale Strömung
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
