Software für Mathematik und Physik,
Grafiken und Animationen
sowie zur numerischen Berechnung, visuellen Analyse, Auswertung, Darstellung und Simulation unterschiedlichster zwei-, wie auch dreidimensionaler technischer, mathematischer und physikalischer Zusammenhänge aller Art.
Interaktiv und dynamisch -
for everyone!
ReduSoft widmet sich seit vielen Jahren der Entwicklung interaktiver 2D- und 3D-Anwendungs- und Simulationssoftware für den naturwissenschaftlichen Bereich. Die Schwerpunkte liegen hierbei in der Erstellung von Programmen zur Analyse und Darstellung mathematischer und physikalischer Gegebenheiten.
Tausende von Einzelanwendern sowie viele Schulen, Firmen und Institutionen verwenden diese Anwendungssoftware zur interaktiven und grafischen Untersuchung von Sachverhalten, zur numerischen Ermittlung von Berechnungsergebnissen aus verschiedenen Bereichen der Mathematik und Physik sowie zur Bereitstellung relevanter Grafiken zu entsprechenden Fachthemen.
I - MathProf 5.0
Mathematik interaktiv
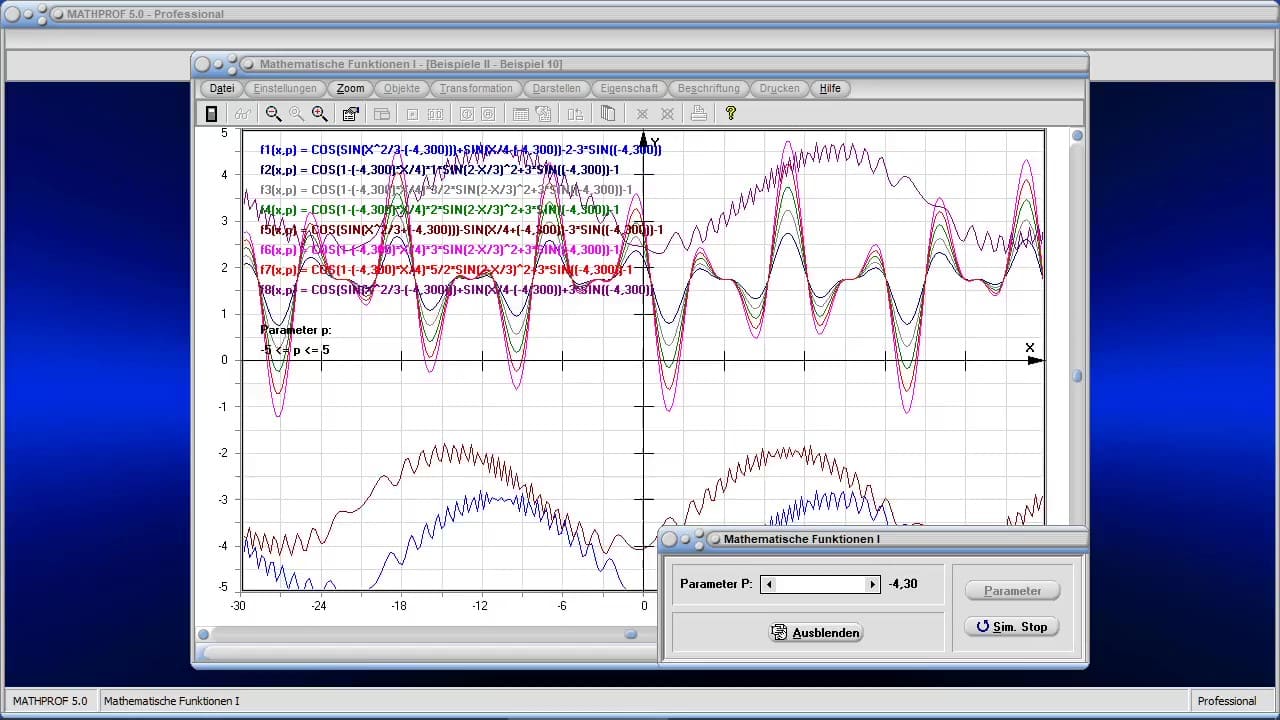
MathProf 5.0 ist ein einfach bedienbares Mathematikprogramm welches es, unter anderem durch die Ausgabe zwei- wie auch dreidimensionaler Darstellungen ermöglicht, sich mathematische Zusammenhänge auf unkomplizierte Weise zu veranschaulichen. Implementiert sind ca. 300 Programmpunkte.
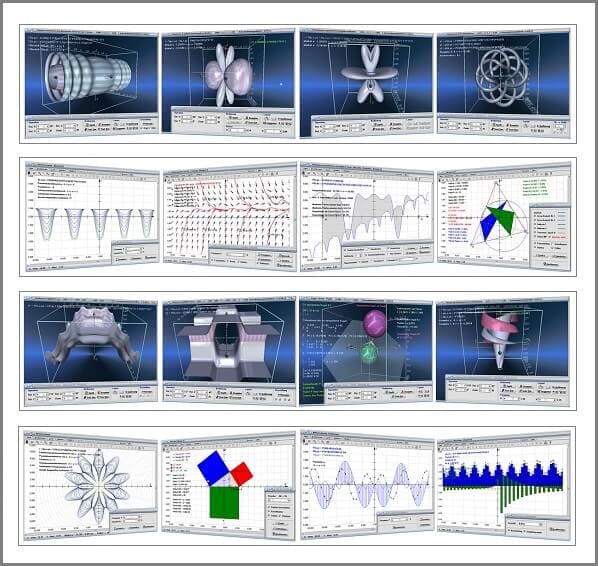
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen.
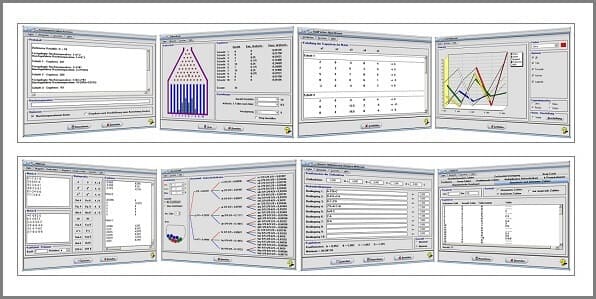
Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
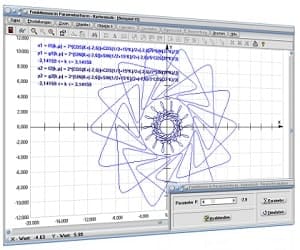 | 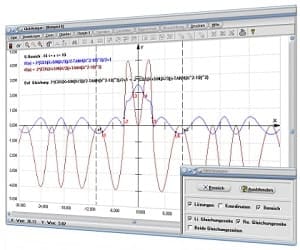 |
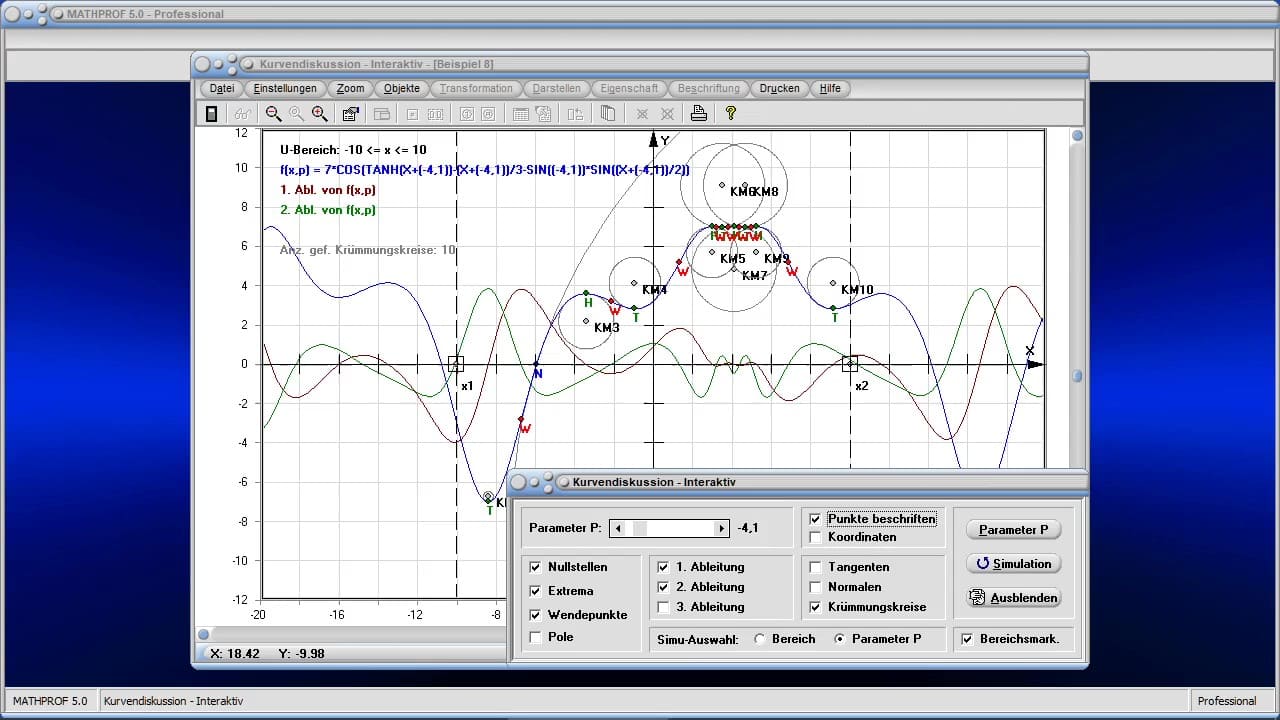
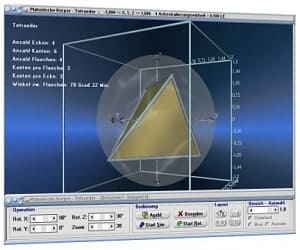
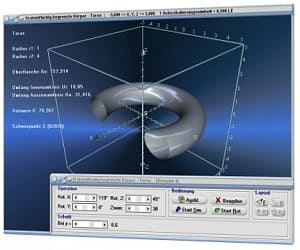
Es enthält sowohl Module zu Themen aus den Bereichen Analysis, Geometrie, Trigonometrie, Stochastik, Algebra, Vektoralgebra und 3D-Mathematik, wie auch Unterprogramme zu anderen mathematischen Fachthemengebieten und stellt ein Werkzeug für Anwender aller Berufs- und Altersklassen dar, um sich Sachverhalte begreiflich zu machen, oder wissenschaftliche Untersuchungen durchzuführen.
 |  |
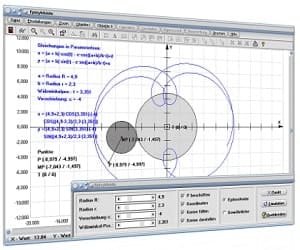
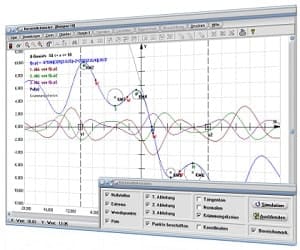
Mit Hilfe dieser Anwendung besteht auch die Möglichkeit, sich abstrakte Zusammenhänge verständlich zu machen und komplexe Sachverhalte zu analysieren. Hierfür wird eine gut strukturierte, intuitive Benutzeroberfläche zur Verfügung gestellt.
 |  |
Neben einfacher Bedienbarkeit und übersichtlicher Strukturierung wird die Möglichkeit geboten, ausgegebene grafische Darstellungen auf vielfältige Art und Weise zu erweitern und anzupassen.
 |  |
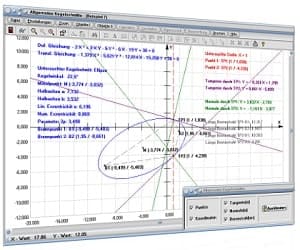
Zudem verfügt es über ein dynamisches Modul, welches die Erstellung zweidimensionaler Konstruktionen und Gebilde mit Hilfe geometrischer Objekte erlaubt. Somit können ausgegebene grafische 2D-Darstellungen in Unterprogrammen in vielfältiger Weise und einfach ergänzt, erweitert oder angepasst werden.
 |  |
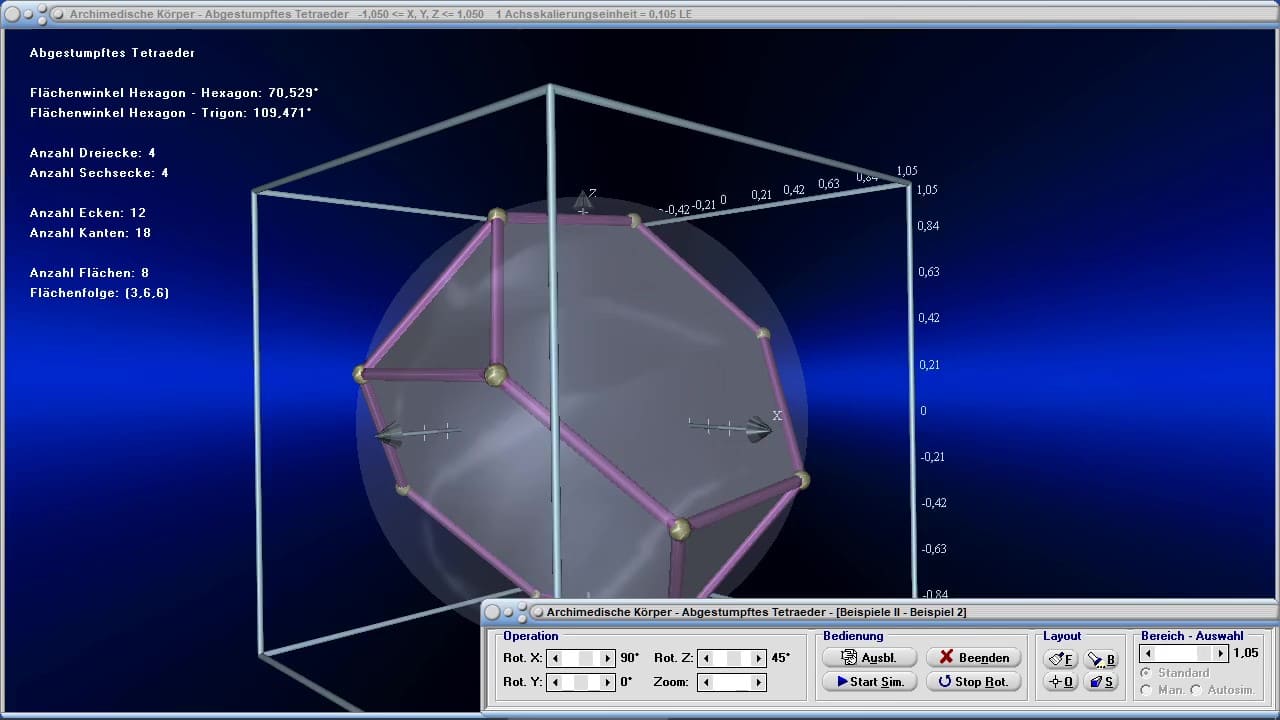
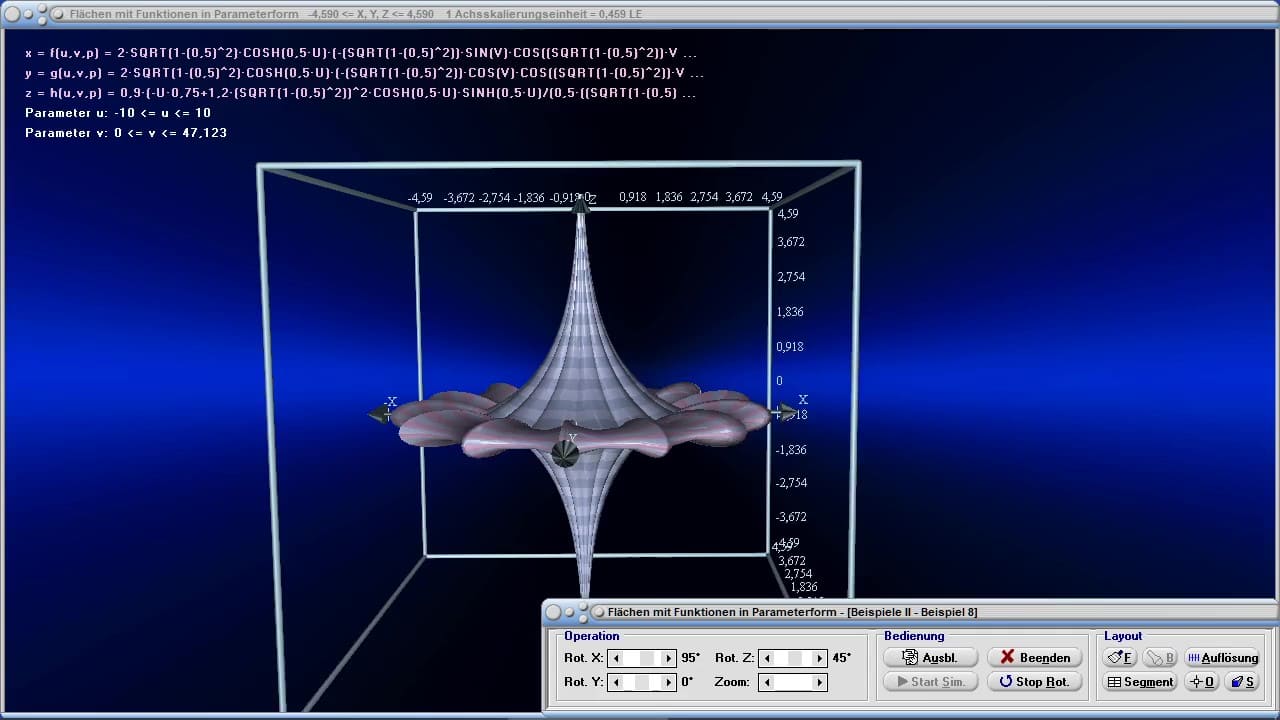
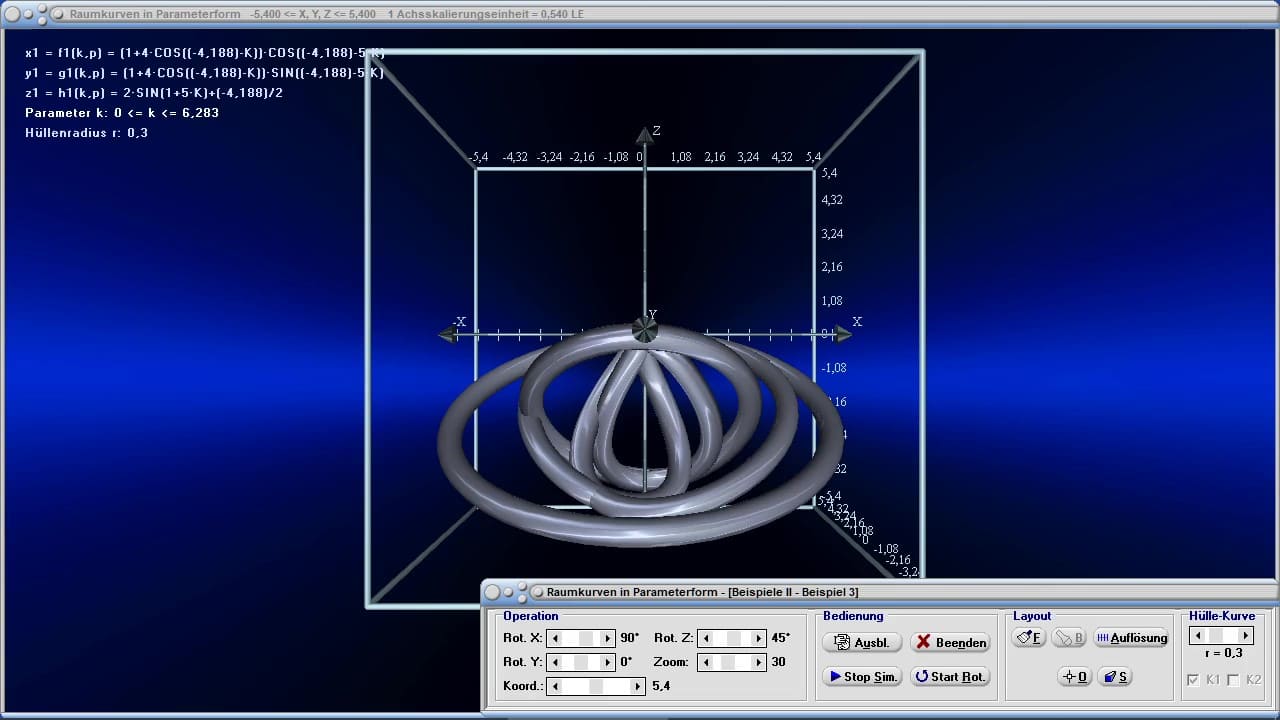
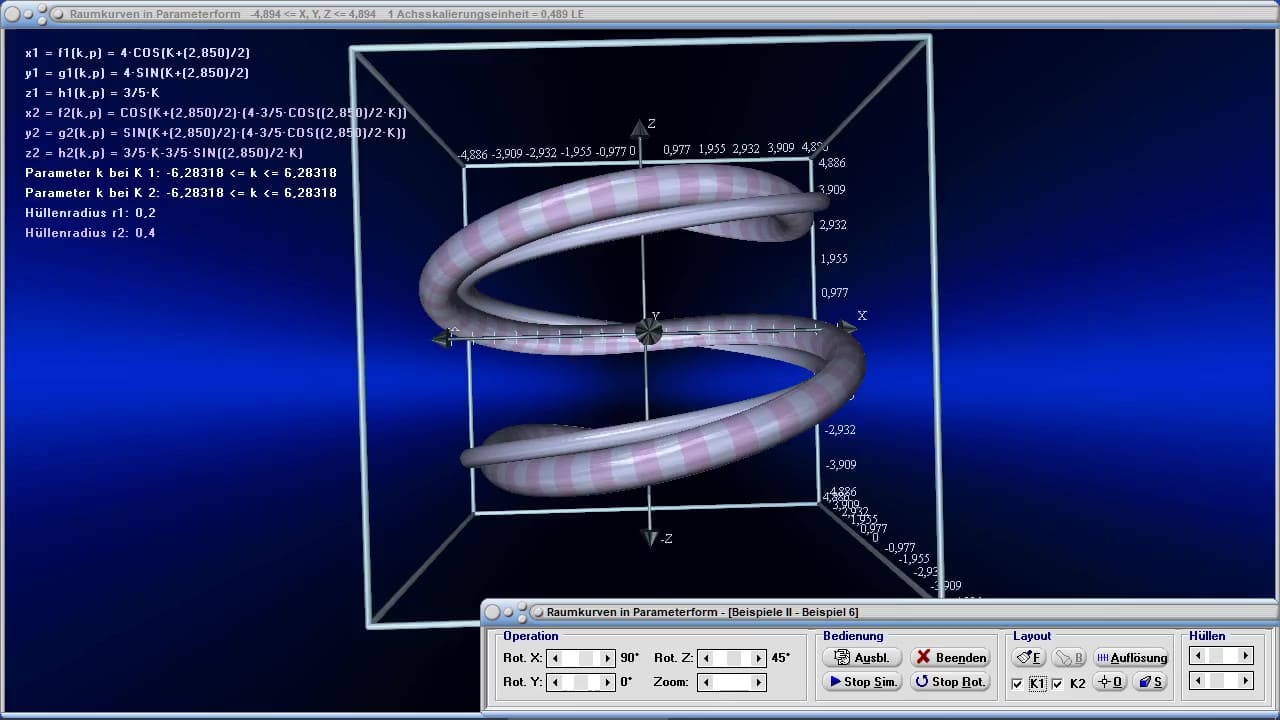
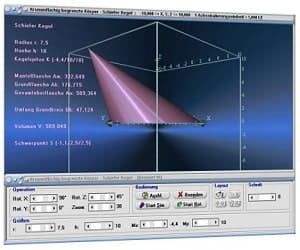
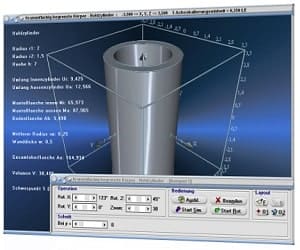
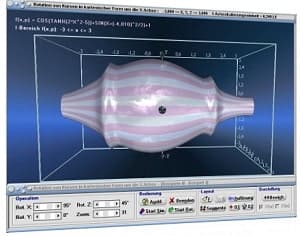
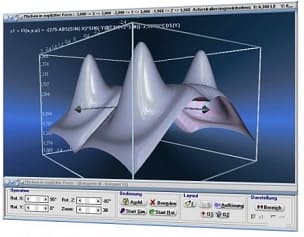
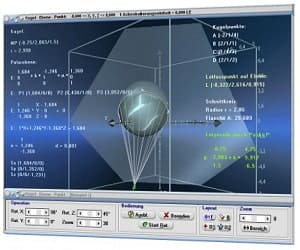
Die Möglichkeit der dreidimensionalen Visualisierung und Untersuchung einfacher, wie komplexer Zusammenhänge bzgl. Themen aus den Bereichen der Körpergeometrie, 3D-Vektoralgebra sowie der Flächen- und Raumkurvendarstellung besteht ebenfalls.
 |  |
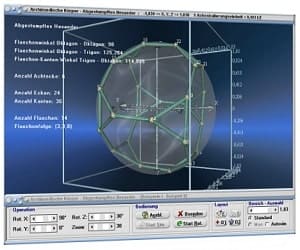 | 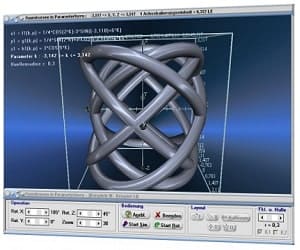 |
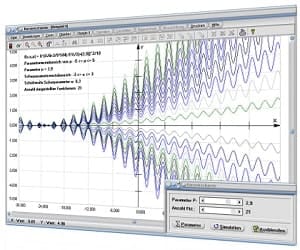
MathProf ermöglicht neben der Durchführung numerischer Analysen die interaktive Untersuchung vieler fachlicher Relationen durch die Ausgabe von 2D- und 3D-Echtzeitdarstellungen beim Ablauf von Simulationen.
 |  |  |  |  |
In vielen Unterprogrammen sind Beispiele eingebunden, durch welche es ermöglicht wird, sich rasch einen Überblick bezüglich der Möglichkeiten zur Verwendung dessen zu verschaffen. Zudem steht eine umfangreiche Online-Hilfe zur Nutzung des Programms zur Verfügung.
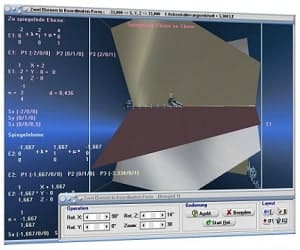 |  |
Kurzinfos zu Inhalten einiger Unterprogramme zu den entsprechenden Teilgebieten der Mathematik erhalten Sie unter:
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Eine kostenlose Demoversion dieses Mathematik-Programms können Sie herunterladen, indem Sie den Reiter Download-Demo aktivieren und hierauf einen Klick auf die dafür vorgesehene Schaltfläche ausführen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
Videos zu MathProf 5.0
Nachfolgend finden Sie eine kleine Auswahl an Videos zu einigen in MathProf 5.0 implementierten Modulen. Durch die Ausführung eines Klicks auf die entsprechende Grafik, können sie dieses abspielen lassen. Weitere Videos zu diesem Programm finden Sie, wenn Sie die hierzu weiter oben angeordnete Schaltfläche Videos anklicken.
Physik interaktiv
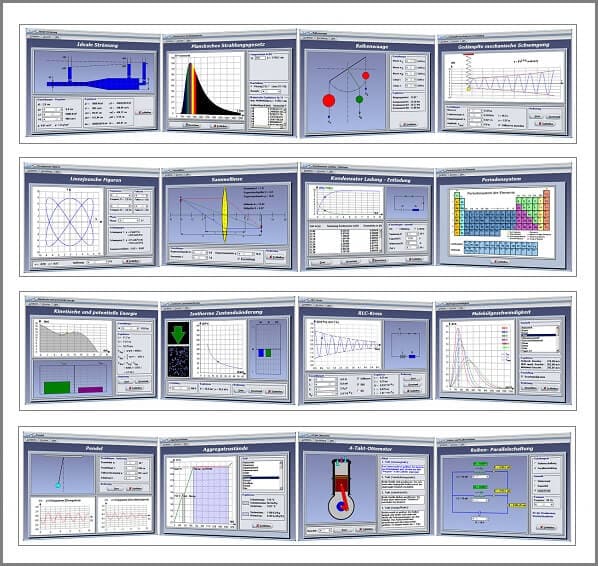
Weiterführende Informationen zu den im Programm PhysProf 1.1 behandelten Fachthemen finden Sie unter PhysProf.
Kurzinfos zu Inhalten einiger Unterprogramme zu den entsprechenden Teilgebieten der Physik erhalten Sie unter:
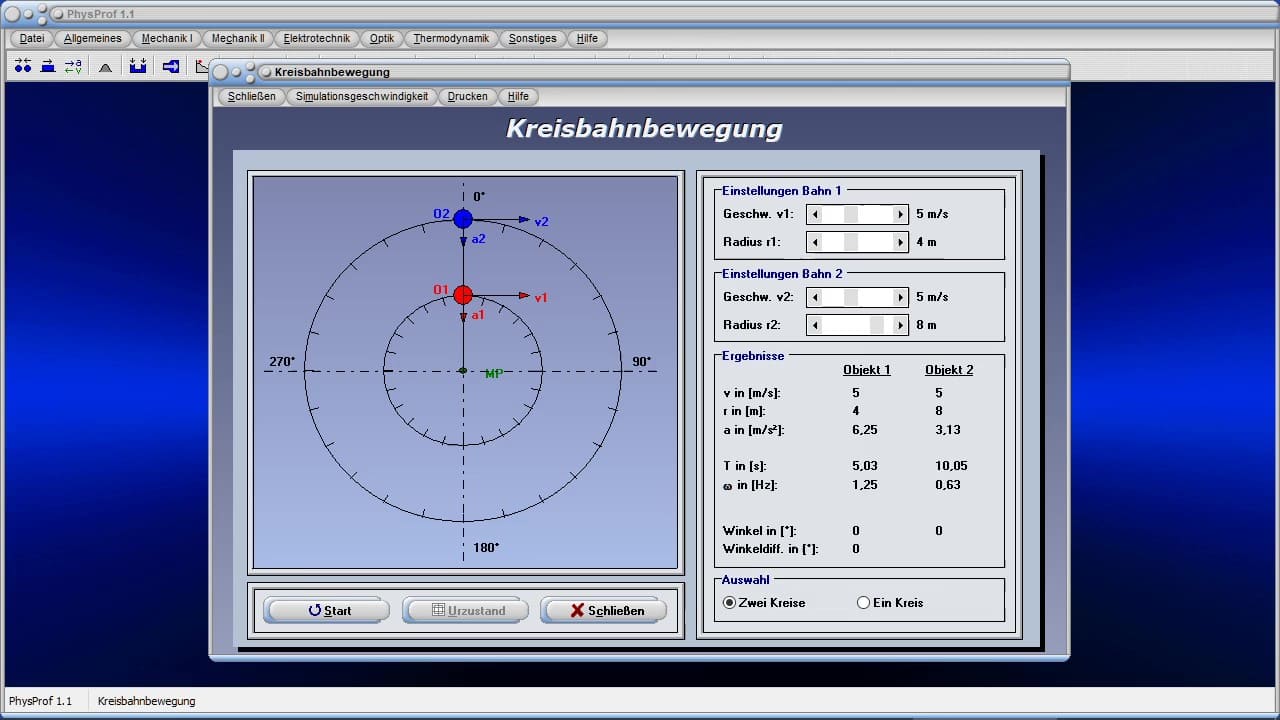
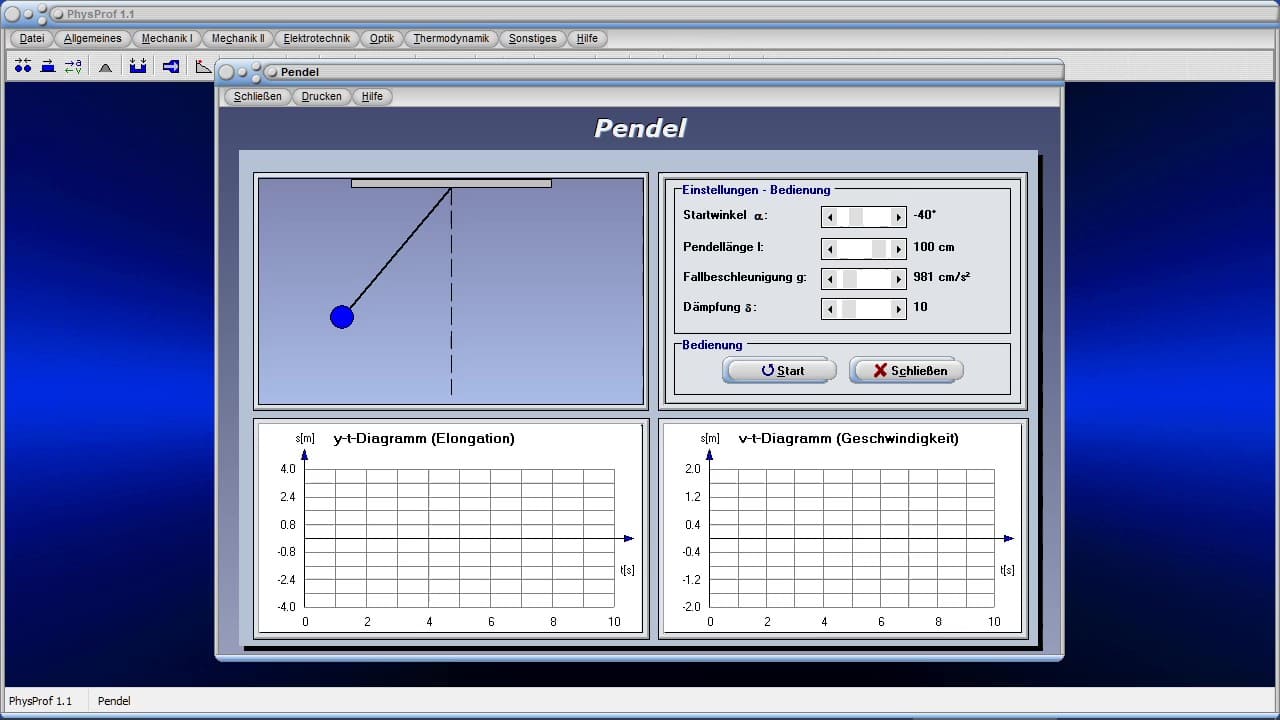
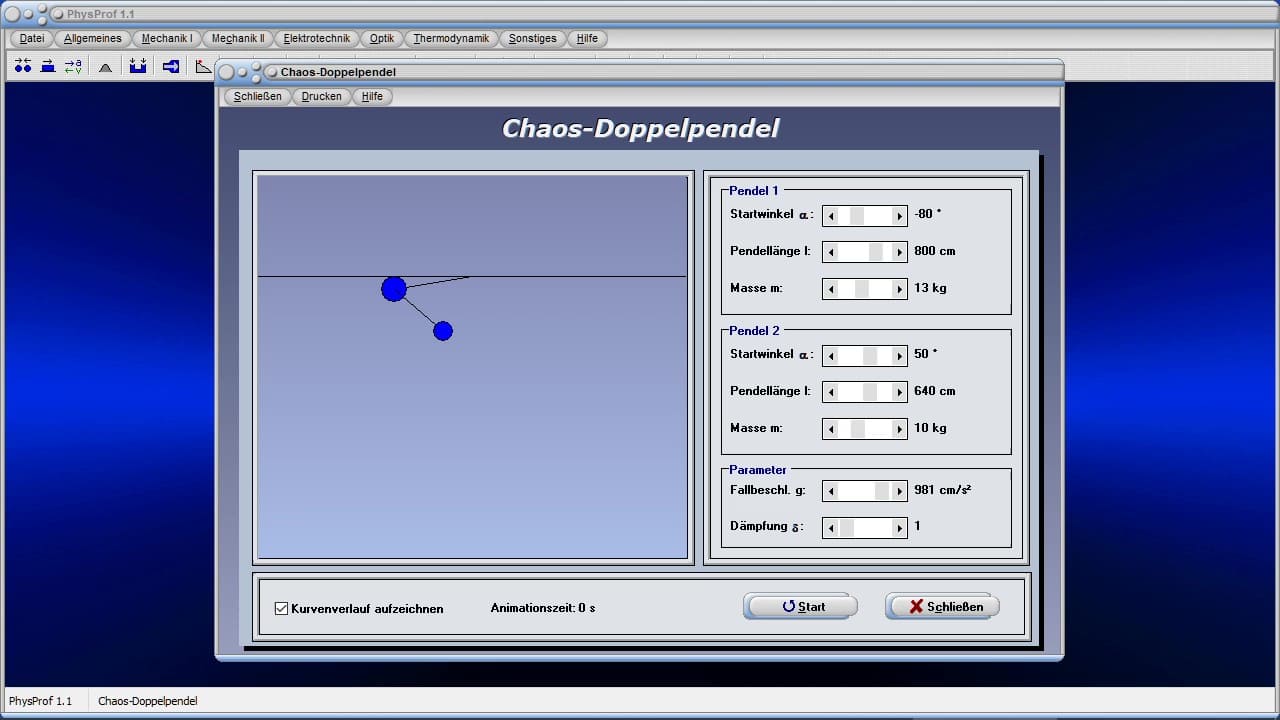
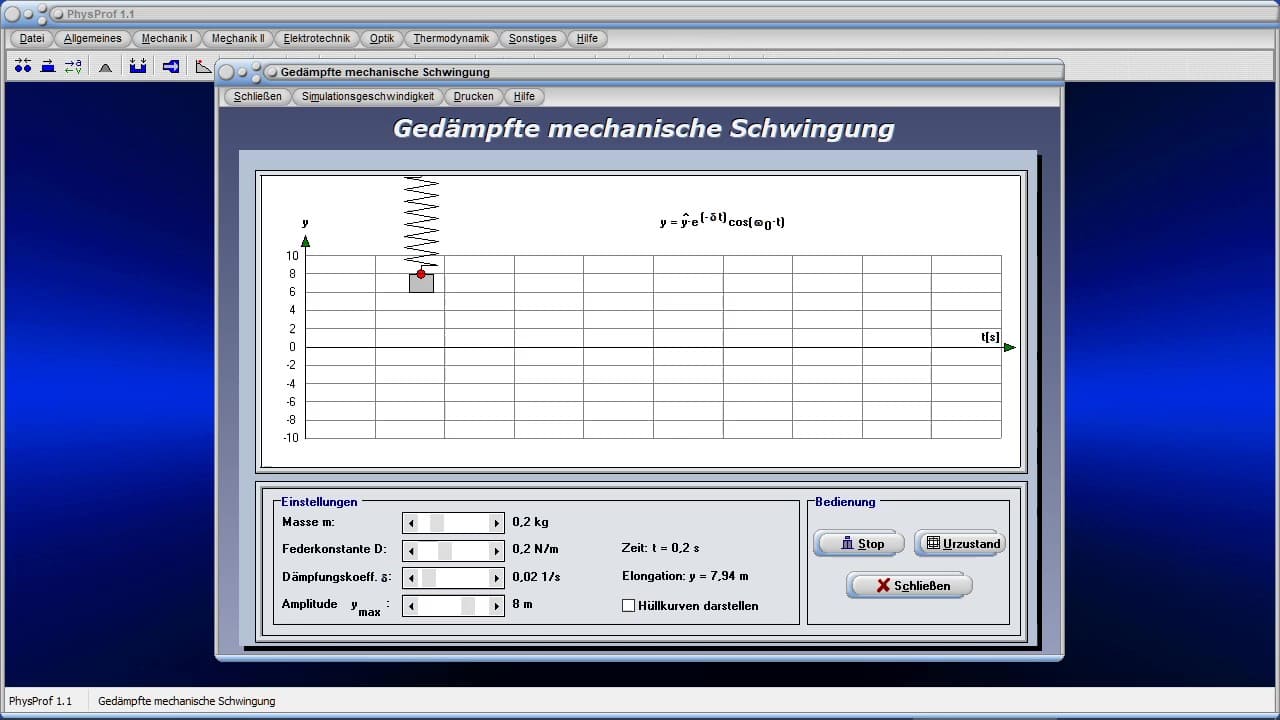
- Kurzinfos zum Themengebiet Mechanik
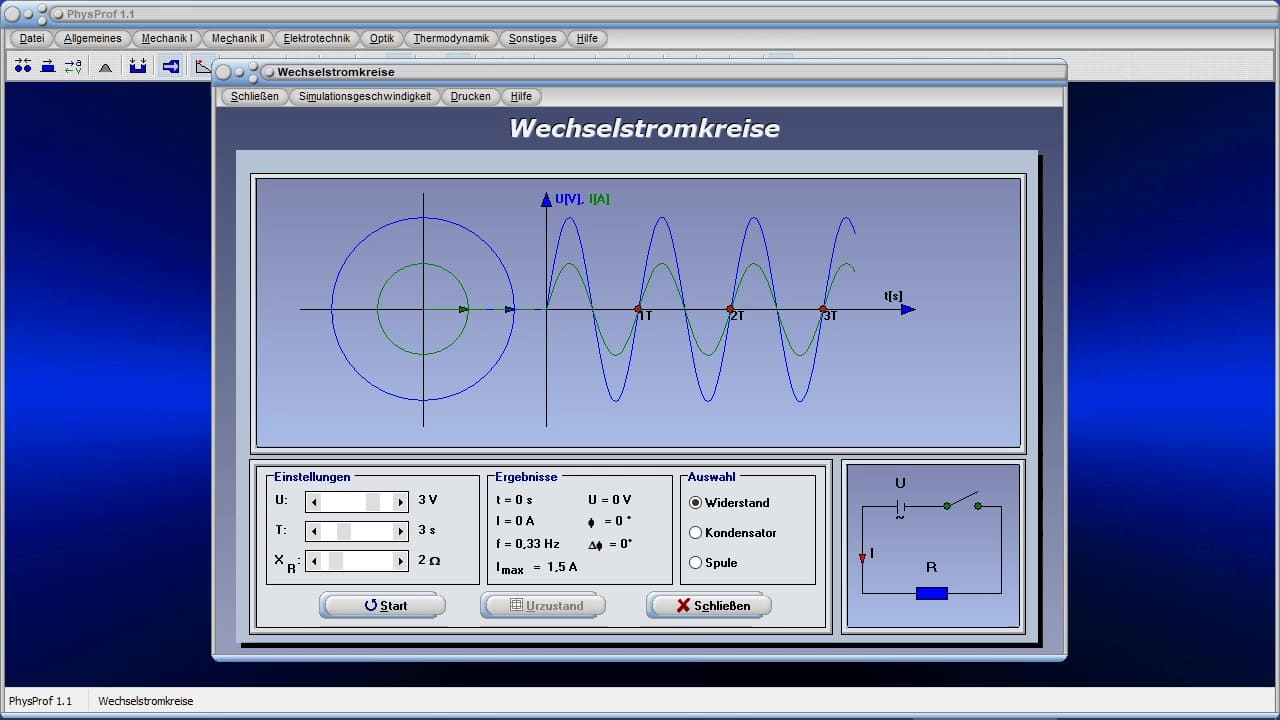
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
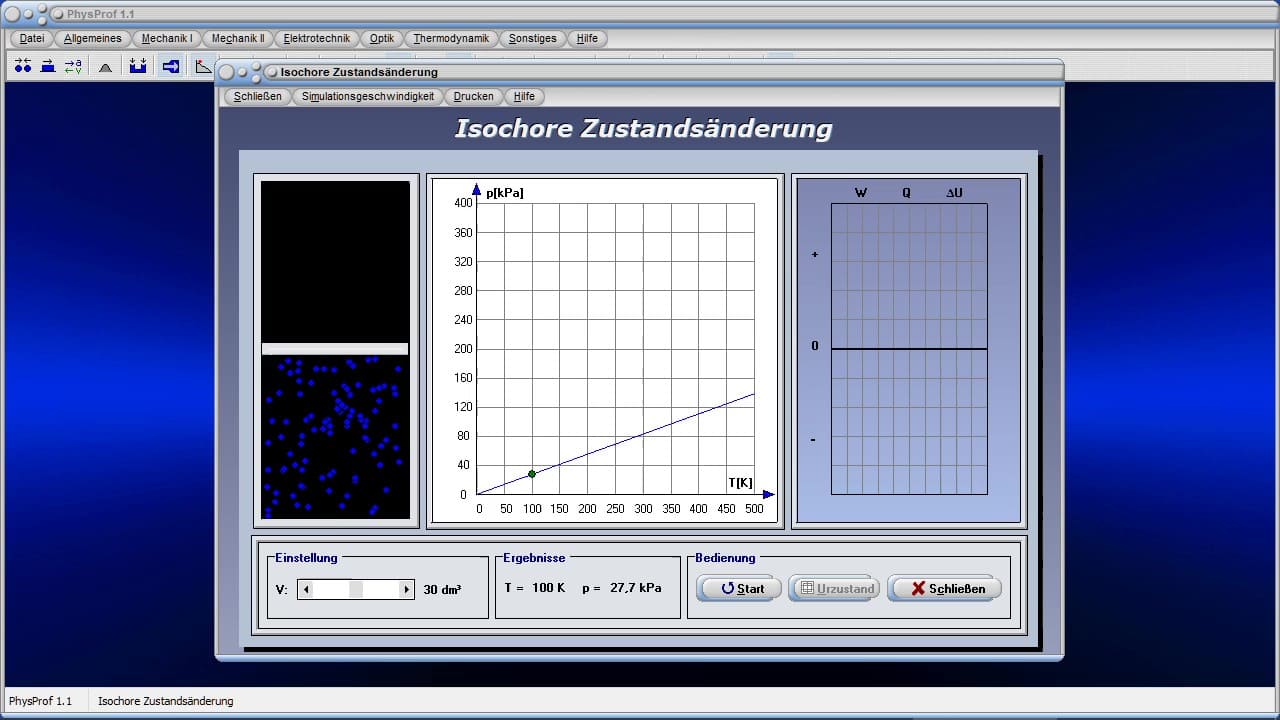
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Videos zu PhysProf 1.1
Nachfolgend finden Sie eine kleine Auswahl an Videos zu einigen in PhysProf 1.1 implementierten Modulen. Durch die Ausführung eines Klicks auf die entsprechende Grafik, können sie dieses abspielen lassen. Weitere Videos zu diesem Programm finden Sie, wenn Sie die hierzu weiter oben angeordnete Schaltfläche Videos anklicken.
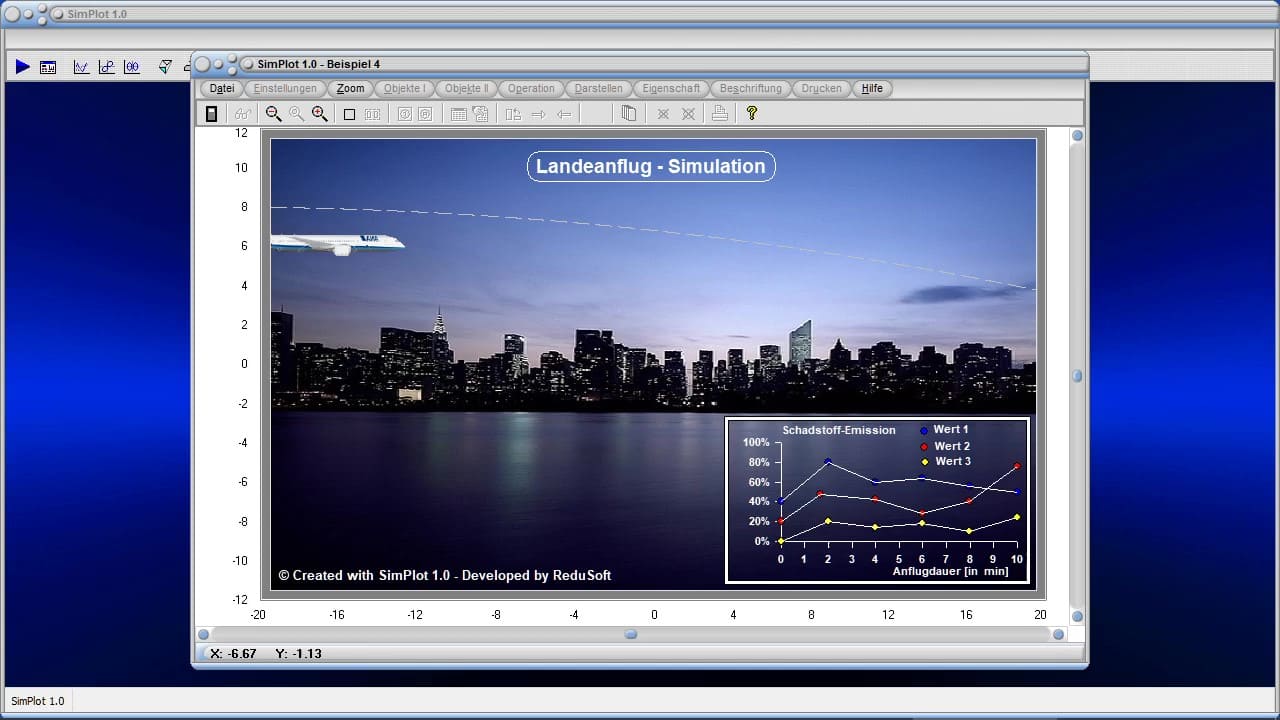
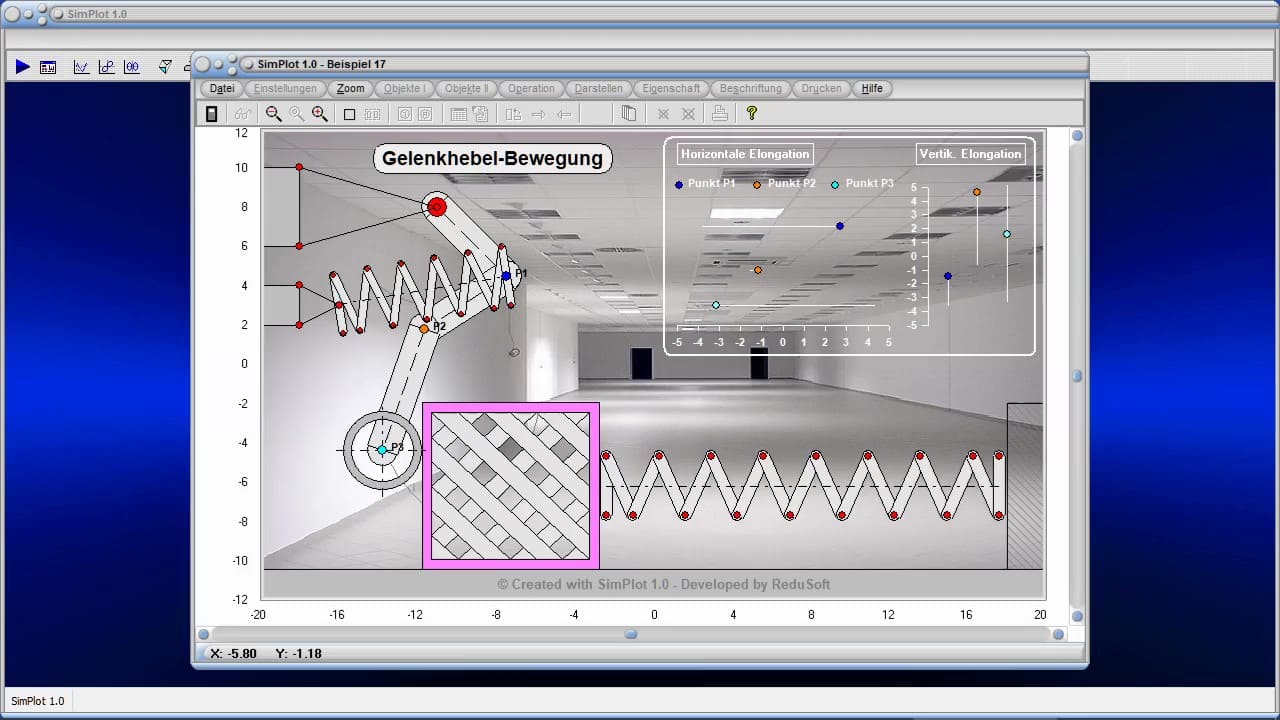
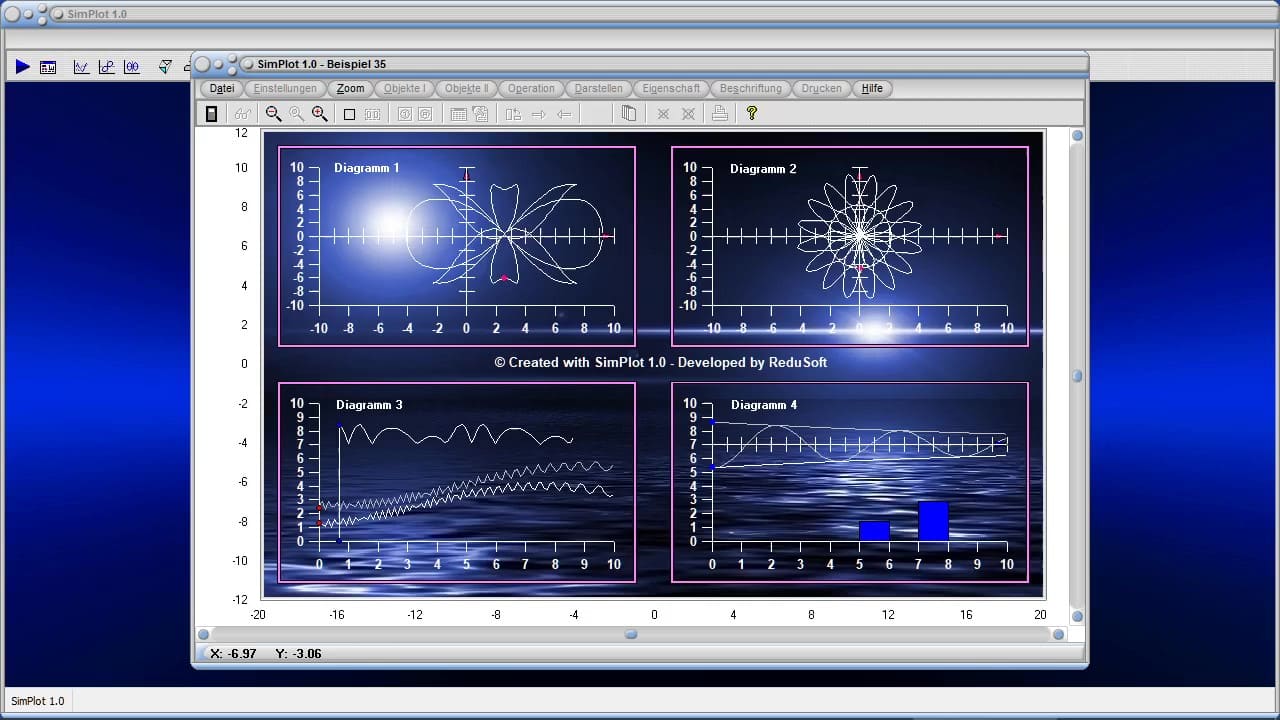
III - SimPlot 1.0
Visualisierung und Simulation interaktiv

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Eine erste Auswahl von Beipielen mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele 1, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
Eine weitere Auswahl von Beipielen mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele 2, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
Videos zu SimPlot 1.0
Nachfolgend finden Sie eine kleine Auswahl an Videos zu einigen in SimPlot 1.0 implementierten Modulen. Durch die Ausführung eines Klicks auf die entsprechende Grafik, können sie dieses abspielen lassen. Weitere Videos zu diesem Programm finden Sie, wenn Sie die hierzu weiter oben angeordnete Schaltfläche Videos anklicken.
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Bestellseite für oben beschriebene Programme.