MathProf - Binomialverteilung - Wahrscheinlichkeit - Bernoulli

Fachthema: Binomialverteilung
MathProf - Stochastik - Statistik - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung der Berechnung von Wahrscheinlichkeiten beim Vorliegen binomialverteilter Zufallsgrößen.
Dieses Teilprogramm ermöglicht die Praktizierung der Wahrscheinlichkeitsrechnung dieser Art durch das Berechnen der Werte derer Dichtefunktion und derer Verteilungsfunktion (kumulierte Wahrscheinlichkeit).
Die Ausgabe dieser erfolgt in einer Tabelle für Einzelwahrscheinlichkeiten und kumulierte Wahrscheinlichkeiten. Die vom Programm ermittelten Lösungen lassen sich ausdrucken.
Zudem erlaubt dieses Unterprogramm die grafische Darstellung der Wahrscheinlichkeitsfunktion (Dichtefunktion) sowie der Wahrscheinlichkeits-Verteilung (Verteilungsfunktion) einer derartigen Verteilung in einem Histogramm in Abhängigkeit relevanter Parameter.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Binomialverteilung - Histogramm - Binomial distribution - Tabelle - Diagramm - Verteilungsfunktion - Verteilungsdichte - Diskrete Verteilungsfunktion - Verteilung - Wahrscheinlichkeitsrechnung - Wahrscheinlichkeitstheorie - Bernoulli-Gleichung - Bernoulli-Experiment - Zufallsexperimente - Zufallsexperiment - Zufallsverteilung - Wahrscheinlichkeitsverteilung - Bernoulli Experiment - Bernoulli-Versuch - Bernoulli-Kette - Bernoulli Kette - Bernoulli Ketten - Erwartungswert - Wahrscheinlichkeitsdichte - Wahrscheinlichkeit - Gegenwahrscheinlichkeit - Eintrittswahrscheinlichkeit - Erfolgswahrscheinlichkeit - Trefferwahrscheinlichkeit - Kumulierte Wahrscheinlichkeit - Zufallsgröße - Bernoulli-Formel - Bernoulli-Verteilung - Kenngröße - Kenngrößen - Zufallsvariable - Diskrete Verteilung - Verlauf - Kumulierte Binomialverteilung - Kumulative Verteilungsfunktion - Summenverteilung - Verteilungstabelle - Dichtetabelle - Dichtefunktion - Binomialverteilt - Grundlagen - Werte - Zufallsvariablen - Binomialverteilte Zufallsgröße - Diskrete Variable - Diskrete Zufallsvariable - Begriff - Begriffe - Kumulierte Häufigkeit - Kumulative Häufigkeit - Summenhäufigkeit - Auswertung - Auswerten - Bild - Statistik - Diagramm - Schaubild - Ablesen - Erstellen - Varianz - Standardabweichung - Intervall - Mindestwahrscheinlichkeit - Summiert - Mindestens - Höchstens - Genau - Exakt - Grafisch - Darstellung - Zufall - Berechnung - Darstellen - Berechnen - Präsentation - Wahrscheinlichkeiten berechnen - Wahrscheinlichkeitsfunktion - Plotter - Funktion - Parameter - Formel - Gleichung - Ablesen - Beispiele - Herleitung - Beweis - Aufgaben - Beispielaufgaben - Was ist - Welche - Welcher - Welches - Wodurch - Wieviel - Bestimmen - Dichte - Graph - Summiert - Kumuliert - 1-p - n = 10 - n = 20 - n = 30 - n = 40 - n = 50 - n = 60 - n = 80 - n = 100 - n = 200 - n = 1000 - Gesucht - Verteilung - Rechner - Ereignis - Was - Wie - Weshalb - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Beschreibung - Definition - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Einführung - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Zeichnen - Tabelle - Quantile - Tabellenform - P - K - N - Zähldichte - Eigenschaften - Stabdiagramm - Symmetrie - Symmetrische Verteilung - Linkssteil - Rechtsschief - Schiefe - Schiefe Verteilung - Linksschief - Rechtssteil - Linksschiefe Verteilung - Rechtsschiefe Verteilung - Wahrscheinlichkeitsrechner - BinomCDF - BinomPDF - PDF - CDF - BinomialPDF - BinomialCDF - Verteilungsdiagramm |
Binomialverteilung
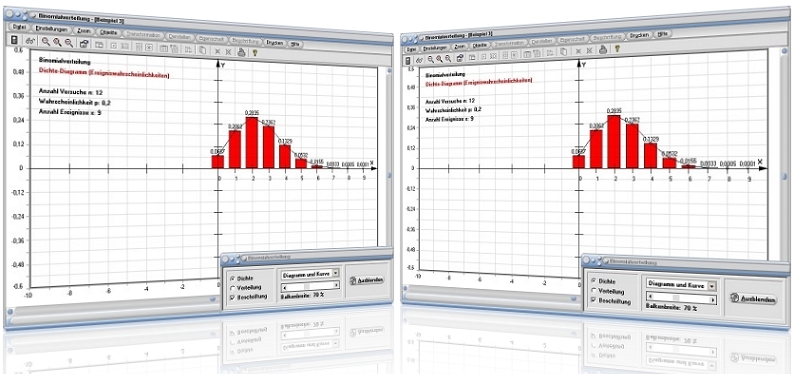
Modul Binomialverteilung
Unter dem Menüpunkt [Stochastik] - [Binomialverteilung] - Binomialverteilung lassen sich Berechnungen mit binomialverteilten Größen durchführen. Ermittelte Werte werden in Tabellen (Wahrscheinlichkeitstabellen) ausgegeben und Zusammenhänge zu diesem Fachthema können grafisch veranschaulicht werden.

Binomialverteilung beschreibt die Wahrscheinlichkeit, welche eintreten kann wenn ein Zufallsexperiment n-mal wiederholt wird, die einzelnen Versuche voneinander unabhängig sind und hierbei ein Ereignis E mit der Ereigniswahrscheinlichkeit p eintreten kann.
Bei einer Binomialverteilung handelt es sich um eine diskrete Verteilung. Eine diskrete Zufallsvariable kann lediglich eine endliche oder abzählbar unendliche Menge an Werten annehmen. Hierbei existiert entweder eine feste Anzahl an Werten (z.B. Würfelwurf), oder es sind dies Zählwerte (z.B: Anzahl an Kunden pro Tag).
Um eine Aufgabe mit einer Binomialverteilung lösen zu können müssen folgene Voraussetzungen erfüllt sein:
- Die durchzuführenden Versuche müssen voneinander unabhängig sein
- Jeder durchgeführte Versuch darf lediglich zwei unterschiedliche Resultate erzeugen (wahr oder falsch bzw. Erfolg oder Misserfolg)
- Die Wahrscheinlichkeit p muss eine konstante Größe besitzen
- Es muss eine bestimmte Anzahl von Versuchen festgelegt sein
Erwartungswert - Diskrete Verteilung
Zufallsgrößen (Zufallsvariablen): Eine Funktion die jedem Ergebnis eines Zufallsexperiments eine reelle Zahl zuordnet wird als Zufallsgröße (Zufallsvariable) bezeichnet. Die Zufallsvariable k heißt binomialverteilt, wenn P(X = k) die Wahrscheinlichkeit ist, dass das Ereignis E genau k-mal bei n durchgeführten Versuchen eintritt.
Für den Erwartungswert E(x) einer Binomialverteilung gilt: E(x) = n · p. Eine Binomialverteilung ist eine diskrete Verteilung. Eine Zufallsvariable heißt diskret, wenn sie in jedem beschränkten Intervall a ≤ x ≤ b lediglich endlich viele Ausprägungen besitzen kann.
Die Varianz V(x) sowie die Standardabweichung σ einer binomialverteilten Zufallsgröße beschreiben deren Abweichung von ihrem Erwartungswert E(x). Deren Berechnung erfolgt mit V(x)= n·p·(1-p) und σ = √n·p·(1-p).
Fachbegriffe
Wahrscheinlichkeitsrechnung (Wahrscheinlichkeitstheorie): Die Wahrscheinlichkeitsrechnung (Wahrscheinlichkeitstheorie) ist ein Themengebiet der Mathematik, bei dem jedem Ereignis eines Zufallsexperiments eine Wahrscheinlichkeit für dessen Eintreten zugeordnet wird.
Verteilungsfunktion: Eine Verteilungsfunktion beschreibt wie groß die Wahrscheinlichkeit ist, dass das Ergebnis eines durchgeführten Zufallsexperiments kleiner oder größer gleich einem bestimmten Wert ist. Sie beschreibt den zwischen einer Zufallsvariablen und derer Wahrscheinlichkeiten bestehenden Zusammenhang. Sie wird auch als kumulative Verteilungsfunktion bezeichnet.
Dichtefunktion: Eine Dichtefunktion beschreibt bei einer diskreten Verteilung, mit welcher Wahrscheinlichkeit eine Zufallsvariable eine bestimmte Merkmalsausprägung annimmt. Eine Dichtefunktion wird auch Wahrscheinlichkeitsdichtefunktion, Wahrscheinlichkeitsdichte, Verteilungsdichte oder Dichte genannt.
Verteilungstabelle: Bei einer Verteilungstabelle handelt es sich um eine Tabelle, die die Werte einer Verteilungsfunktion enthält.
Dichtetabelle: Eine Dichtetabelle ist eine Tabelle, die die Werte einer Dichtefunktion beinhaltet.
Histogramm (Verteilungsdiagramm): Bei einem Histogramm handelt es sich um ein Säulendiagramm, mit Hilfe dessen sich Wahrscheinlichkeitsverteilungen grafisch veranschaulichen lassen. Jedem sich auf der x-Achse eines Koordinatensystems befindenden Wert einer Zufallsvariable wird eine vertikale Säule zugeschrieben. Die Höhe einer Säule entspricht der Wahrscheinlichkeit, mit der dieser Wert angenommen wird. Weist das Erscheinen eines Histogramms eine Symmetrie bezüglich eines Werts auf, so handelt es sich hierbei um den Erwartungswert der Verteilung.
Diskrete Verteilung und diskrete Zufallsvariable: Eine diskrete Verteilung beschreibt die Wahrscheinlichkeit, mit welcher einzelne Werte einer diskreten Zufallsvariablen auftreten. Bei einer diskreten Zufallsvariable handelt es sich um eine Zufallsvariable, die ausschließlich zählbare Werte annehmen kann, natürliche Zahlen. Eine Variable dieser Art wird auch als diskrete Variable bezeichnet. Diskrete Variablen sind Zahlen, die zwischen zwei beliebigen Werten eine abzählbare Anzahl von Werten aufweisen.
Erwartungswert: Der Erwartungswert einer Zufallsvariablen teilt mit, welcher durchschnittliche Wert (Mittelwert) bei einer großen Häufigkeit von Durchführungen eines Zufallsexperiment für die Zufallsvariable zu erwarten ist.
Zufallsexperimente: Bei einem Zufallsexperiment handelt es sich um einen Versuch, der unter exakt festgelegten Bedingungen durchgeführt wird und einen zufälligen Ausgang besitzt. Es handelt sich um einen Vorgang, der über mehr als einen möglichen Ausgang (ein mögliches Ergebnis) verfügen kann. Es kann jedoch nicht vorhergesagt werden, welches Resultat das durchgeführte Zufallsexperiment besitzen wird.
Als Wahrscheinlichkeitsverteilung (Zufallsverteilung) wird eine Funktion bezeichnet, die den Resultaten eines Zufallsexperiments deren Wahrscheinlichkeiten zuordnet.
Eintrittswahrscheinlichkeit (Ereigniswahrscheinlichkeit): Als Eintrittswahrscheinlichkeit wird der Erwartungswert oder die geschätzte Wahrscheinlichkeit für das Eintreten eines bestimmten Ereignisses innerhalb eines bestimmten Zeitraums in der Zukunft bezeichnet. Sie wird in Prozentzahlen oder als ein Wert zwischen 0 und 1 angegeben.
Erfolgswahrscheinlichkeit (Trefferwahrscheinlichkeit): Als Erfolgswahrscheinlichkeit oder Trefferwahrscheinlichkeit wird die Wahrscheinlichkeit P(A) des Eintretens eines bestimmten Ereignisses A bei der Durchführung eines zufälligen Experiments bezeichnet.
Kumulierte Wahrscheinlichkeit: Als kumulierte Wahrscheinlichkeit wird die Summe mehrerer Wahrscheinlichkeiten bezeichnet (lat. cumulus: Anhäufung). Eine kumulierte Binomialverteilung wird benutzt, um eine Wahrscheinlichkeit von höchstens k Treffern bei der Durchführung eines Zufallsexperiments zu bestimmen. Eine kumulierte Wahrscheinlichkeitsverteilung wird auch als Summenverteilung bezeichnet.
Kumulierte Häufigkeit (Summenhäufigkeit): Die kumulierte Häufigkeit oder Summenhäufigkeit beschreibt bei Durchführung einer empirischen Untersuchung die Anzahl der Merkmalsträger deren Merkmalsausprägung geringer ist als eine bestimmte Schranke. Sie wird durch die Bildung der kumulativen Summe aller Häufigkeiten gebildet, indem diese hierbei bis zu einem festgelegten Datensatz gebildet wird. Sie wird auch als kumulative Häufigkeit bezeichnet. Die Ermittlung dieser kumulativen Häufigkeit unterscheidet sich vom Wert der absoluten Häufigkeit insofern, dass sich die Häufigkeit im letzter genannten Fall auf die Anzahl der Erscheinungen eines bestimmten Werts in einem Datensatz bezieht.
Kenngröße: Als Kenngrößen werden verschiedene Verteilungsparameter bezeichnet, die Unterschiedliches beschreiben und somit unterschiedliche Resultate liefern können. Eine Kenngröße ist ein Merkmal, das Aussagen über bestimmte Eigenschaften liefert. Dies können sowohl qualitative wie auch quantitative Eigenschaften sein.
Stabdiagramm. Ein Stabdiagramm ermöglicht die anschauliche grafische Darstellung statistischer Größen gemäß ihrer sachlichen (zeitlichen) Folge.
Bernoulli - Trefferwahrscheinlichkeit - Erfolgswahrscheinlichkeit
Als Bernoulli-Experiment (Bernoulli-Versuch bzw. Bernoulli Versuch) wird ein Zufallsexperiment bezeichnet, welches exakt zwei unterschiedliche Ergebnisse ermöglicht. Dies kann ein Treffer oder eine Niete bzw. ein Erfolg oder ein Misserfolg sein.
Beispiele für ein derartiges Experiment sind:
- Wurde beim Münzwurf ein Kopf oder eine Zahl gezogen
- Wurde beim Würfeln eine Sechs erzielt?
- Wurde die Prüfung bestanden?
Wird ein derartiges Experiment mehrmalig durchgeführt, so wird von einem n-stufigen Bernoulli-Experiment (Bernoulli Experiment) gesprochen. Dieser Fall wird auch als Bernoulli-Kette (Bernoulli Kette) von einer Länge n bezeichnet. In diesem Fall gilt für die Wahrscheinlichkeit k Treffer zu erzielen:
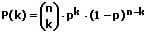
p ist die Wahrscheinlichkeit zum Erzielen eines Treffers, p-1 ist die Gegenwahrscheinlichkeit hierfür.
Die Wahrscheinlichkeit des Eintretens eines Ereignisses (Trefferwahrscheinlichkeit bzw. Erfolgswahrscheinlichkeit) wird in diesem Fall wie folgt mit der Bernoulli-Formel bzw. der Wahrscheinlichkeitsfunktion (Zähldichte) oder Dichte beschrieben:
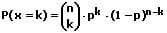
Oftmals gilt es Fragen zu beantworten, mit welcher Wahrscheinlichkeit ein Ereignis mindestens, oder höchstens zu erwarten ist, z.B. P(X ≤ k) oder P(X ≥ k). Hierfür wird die Verteilungsfunktion verwendet. Diese Verteilung (kumulierte Wahrscheinlichkeit) wird hierbei beschrieben mit der Verteilungsfunktion:
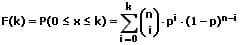
Der Erwartungswert der Binomialverteilung errechnet sich wie folgt:
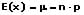
Symmetrische Verteilung: Als symmetrische Verteilungen werden Wahrscheinlichkeitsverteilungen bezeichnet, die sich dadurch auszeichnen, dass die Wahrscheinlichkeit, einen Wert zu erhalten, der kleiner als -x ist, immer gleich groß ist wie die Wahrscheinlichkeit, einen Wert größer als x zu erhalten.
Linksschiefe Verteilung und rechtsschiefe Verteilung: Besitzt eine Verteilung eine symmetrische Häufigkeitsverteilung, so wird sie als symmetrisch bezeichnet. Ist die Konzentration dieser bei einer Häufigkeitsverteilung auf der linken Seite jedoch stärker, so liegt eine schiefe Verteilung vor und man nennt diese Verteilung linkssteil bzw. rechtsschief. Im umgekehrten Falls hingegen trägt sie die Bezeichnung rechtssteil bzw. linksschief.
Eine Bernoulli-Verteilung ist ein Sonderfall der Binomialverteilung. Diese liegt vor, wenn die Zufallsvariable k nur einen der beiden Werte wahr oder falsch annehmen kann. Diese liegt vor, wenn die Anzahl der Versuche bei n = 1 liegt.
Die Gegenwahrscheinlichkeit einer Erfolgswahrscheinlichkeit beträgt 1−p. Sie ist die Wahrscheinlichkeit des Eintretens eines Gegenereignisses.
Als Mindestwahrscheinlichkeit wird die Wahrscheinlichkeit bezeichnet, die zu mindestens einem Treffer führt.
Berechnung
Per Voreinstellung (ohne die Aktivierung des Kontrollkästchen Alle Ereigniswahrscheinlichkeiten) gibt das Programm in diesem Modul nach Ausführung eines Klicks auf die Schaltfläche Berechnen die Wahrscheinlichkeit P(X = k) mit der dieses Ereignis genau k-mal eintritt, aus. Zudem werden die Wahrscheinlichkeiten ausgegeben, mit welchen das Auftreten dieses Ereignisses bis zu k-mal, oder höchstens k-mal eintritt F(X ≤ k).
Alle Ereigniswahrscheinlichkeiten

Interessieren weitere Ereigniswahrscheinlichkeiten, wie
- Wahrscheinlichkeit, mit der ein Ereignis genau k-mal eintritt
- Wahrscheinlichkeit, mit der ein Ereignis mindestens k-mal eintritt
- Wahrscheinlichkeit, mit der ein Ereignis mehr als k-mal eintritt
- Wahrscheinlichkeit, mit der ein Ereignis weniger als k-mal eintritt
so können Sie sich auch diese ausgeben lassen und ablesen, nachdem vor der Ausführung eines Klicks auf díe Schaltfläche Berechnen das Kontrollkästchen Alle Ereigniswahrscheinlichkeiten aktiviert wurde. Hierbei gelten folgende Zusammenhänge:
Wahrscheinlichkeit, mit welcher ein Ereignis genau k-mal eintritt:
F(0) für k = 0
F(k) - F(k-1) für k ≥ 1
Wahrscheinlichkeit, mit welcher ein Ereignis mindestens k-mal eintritt:
1 für k = 0
1 - F(k-1) für k ≥ 1
Wahrscheinlichkeit, mit welcher ein Ereignis mehr als k-mal eintritt:
1 - F(k)
Wahrscheinlichkeit, mit welcher ein Ereignis weniger als k-mal eintritt:
F(k-1)
Berechnung und Darstellung - Schaubilder

Grafische Darstellung - Beispiel 1 - Dichte - Histogramm - Schaubild

Grafische Darstellung - Beispiel 2 - Verteilung - Histogramm - Schaubild
Um in disem Modul Berechnungen mit binomialverteilten Größen durchführen zu lassen und Zusammenhänge grafisch zu analysieren, gehen Sie wie nachfolgend beschrieben vor:
- Legen Sie im Feld Anzahl Versuche n die Anzahl durchzuführender Versuche fest. Geben Sie in das Feld Wahrscheinlichkeit p die Wahrscheinlichkeit ein, mit welcher das interessierende Ereignis eintritt und tragen Sie in das Feld Anzahl Ereignisse x die Anzahl aufgetretener Ereignisse ein.
- Bedienen Sie die Schaltfläche Berechnen und ist das Kontrollkästchen Alle Ereigniswahrscheinlichkeiten deaktiviert, so werden die entsprechenden Ergebnisse für die Ereigniswahrscheinlichkeiten P(X = k), sowie für die Verteilung F(X ≤ k) für k = 1...x in den Tabellen ausgegeben.
Möchten Sie sich alle Arten berechenbarer Ereigniswahrscheinlichkeiten ausgeben lassen, so aktivieren Sie vor Durchführung der Berechnung das Kontrollkästchen Alle Ereigniswahrscheinlichkeiten. Die in Tabelle p2 aufgelisteten Ereigniswahrscheinlichkeiten entsprechen den, auf dem Hauptformular des Unterprogramms in Tabelle Ereigniswahrscheinlichkeiten p(X=k), angezeigten Wahrscheinlichkeitswerten.
- Nach einer Bedienung der Schaltfläche Darstellen stellt das Programm das Diagramm für die Dichtefunktion (Wahrscheinlichkeitsdichte) dieser Verteilung in einem Histogramm dar (Kontollschalter Dichte ist aktiviert). Um das entsprechende Verteilungsdiagramm angezeigt zu bekommen, aktivieren Sie den Kontrollschalter Verteilung.
Hinweis:
Sollen alle Ereigniswahrscheinlichkeiten für die festgelegte Anzahl von Ereignissen errechnet werden, so sind in die Eingabefelder Anzahl Ereignisse x und Anzahl Versuche n gleiche Werte einzugeben.
Bedienformular

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Benutzung der entsprechenden Steuerelemente folgende zusätzliche Einstellungen vornehmen:
- Diagramm und Kurve: Darstellung des Verteilungs- oder Dichtediagramms in Form von Balken und Linien
- Nur Kurve: Darstellung des Verteilungs- oder Dichtediagramms in Form von Linien
- Nur Diagramm: Darstellung des Verteilungs- oder Dichtediagramms in Form von Balken
- Balkenbreite: Einstellung der Balkenbreite des entsprechenden Diagramms
- Beschriftung: Anzeige der Verteilungs- bzw. Dichtewerte ein-/ausschalten
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann.Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Weitere Themenbereiche
Binomialverteilung - grafische Analyse
Beispiele - Aufgaben
Bimomialverteilung - Beispiel 1:
Wie groß ist die Wahrscheinlichkeit, mit einem Würfel bei 5-maligen Werfen, genau 3 mal eine 6 zu werfen?
Mit p = 1/6 kann festgelegt werden:
n = 5
p = 0,166666
x = 3
Vorgehensweise und Lösung:
Nach Eingabe dieser Werte in die entsprechenden Felder, einer Deaktivierung des Kontrollkästchens Alle Ereigniswahrscheinlichkeiten und der Bedienung der Schaltfläche Berechnen kann aus der Tabelle mit der Bezeichnung Ereigniswahrscheinlichkeiten p(X=k) entnommen werden, dass die Wahrscheinlichkeit hierfür ca. 3,215% beträgt.
P(X=3) = 0,032149
Bimomialverteilung - Beispiel 2:
Ein Schüler hat für einen Multiple-Choice-Test nicht gelernt. Der Test besteht aus 10 Fragen mit je 4 Antworten. Es ist jeweils genau eine Antwort richtig. Wie groß ist die Wahrscheinlichkeit, dass der Schüler mindestens die Hälfte der Fragen richtig beantwortet.
Vorgehensweise und Lösung:
Es handelt sich um eine Binomialverteilung mit den Parametern n = 10 und p = 1/4 = 0,25. Somit sind die Eingabefelder mit folgenden Werten zu belegen:
n = 10
p = 0,25
x = 10 (mindestens jedoch 5)
Hierauf ist das Kontrollkästchen Alle Ereigniswahrscheinlichkeiten zu aktivieren und die Schaltfläche Berechnen zu bedienen.
Da es sich um eine Wahrscheinlichkeit handelt, mit welcher ein Ereignis mindestens k-mal eintritt, und für k der Wert 5 (mindestens die Hälfte von 10) zu wählen ist, gilt bei der Suche nach dem entsprechenden Tabelleneintrag:
1 - F(k-1) für k ≥ 1
1- F(5-1) = 1-F(4)
Aus dem Eintrag 1-F(4) in Tabelle p3 kann somit entnommen werden, dass die Wahrscheinlichkeit mindestens die Hälfte aller Fragen richtig zu beantworten P(X ≥ 5) = 1-F(4) = 0,07812 beträgt (7,812 %).
Diese Wahrscheinlichkeit kann auch durch eine Aufsummierung der entsprechenden Einzelwahrscheinlichkeiten mit den Nummern 5-10 in der Tabelle Ereigniswahrscheinlichkeiten p(X=k) ermittelt werden, da gilt: P(X ≥ 5) = P(X = 5) + P(X = 6) + ... + P(X = 10)
Bimomialverteilung - Beispiel 3:
In einer Urne befinden sich 30 verschiedenfarbige Kugeln, von welchen 10 die Farbe rot besitzen. Die Wahrscheinlichkeit eine rote Kugel zu ziehen liegt hiermit bei 0,33333333. Das Ziehen einer Kugel (mit darauffolgendem Zurücklegen) wird 10-mal durchgeführt.
Mit welcher Wahrscheinlichkeit werden am häufigsten 3, 5 oder 8 rote Kugeln gezogen?
Vorgehensweise und Lösung:
3 Kugeln:
n = 10
p = 0,3
x = 3
Nach Eingabe dieser Werte in die entsprechenden Felder, einer Aktivierung des Kontrollkästchens Alle Ereigniswahrscheinlichkeiten und der Bedienung der Schaltfläche Berechnen kann aus der Tabelle mit der Bezeichnung p2 unter dem Eintrag F(3) - F(2) entnommen werden, dass die Wahrscheinlichkeit hierfür 26,683% beträgt.
5 Kugeln:
n = 10
p = 0,3
x = 5
Nach Eingabe dieser Werte in die entsprechenden Felder, einer Aktivierung des Kontrollkästchens Alle Ereigniswahrscheinlichkeiten und der Bedienung der Schaltfläche Berechnen kann aus der Tabelle mit der Bezeichnung p2 unter dem Eintrag F(5) - F(4) entnommen werden, dass die Wahrscheinlichkeit hierfür 10,292% beträgt.
8 Kugeln:
n = 10
p = 0,3
x = 8
Nach Eingabe dieser Werte in die entsprechenden Felder, einer Aktivierung des Kontrollkästchens Alle Ereigniswahrscheinlichkeiten und der Bedienung der Schaltfläche Berechnen kann aus der Tabelle mit der Bezeichnung p2 unter dem Eintrag F(8) - F(7) entnommen werden, dass die Wahrscheinlichkeit hierfür 0,145% beträgt.

Grafische Darstellung - Beispiel 3 - Dichte

Grafische Darstellung - Beispiel 4 - Verteilung

Grafische Darstellung - Beispiel 5 - Dichte
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Binomialverteilung zu finden.
Kombinatorik - Urnenmodell - Pfadregel - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Regressionsanalyse - Stichproben - Stichproben - Verteilungen - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)
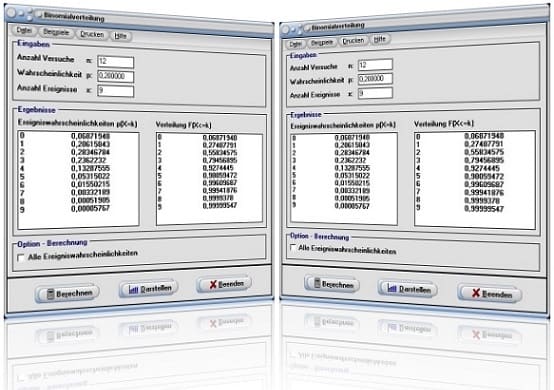
Startfenster des Unterprogramms Binomialverteilung
MathProf 5.0 - Unterprogramm Binomialkoeffizient

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















