PhysProf - Thermometer - Dehnung - Heizwert - Wärmeinhalt - Wärmemenge

Fachthemen: Mischungsregel - Ausdehnung - Wärmeübertragung - Wärmemenge - Wärmemenge - Wärmeinhalt - Wärmekapazität - Temperatur - Bimetall - Heizwert

PhysProf - Thermodynamik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Realschule, das Berufskolleg, das Gymnasium, das Studium sowie für alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Durchführung einfacher Berechnungen zum Wärmeaustausch zweier Körper.

Das Programm ermittelt die gemeinsame Temperatur zweier flüssiger Stoffe, über welche diese nach deren Mischung verfügen.

Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

 

Themen und Stichworte zu diesem Modul: Wärme - Mischungsregel - Erwärmungsgesetz - Mischtemperatur - Flüssigkeiten - Mischung - Mischungsrechnung - Mischungsrechnen - Substanzen - Wärmeaustausch - Berechnen - Temperatur - Masse - Richmannsche Mischungsregel - Temperaturdifferenz - Temperaturunterschied - Temperaturumrechnung - Temperatur umrechnen - Celsius - Fahrenheit - Kelvin - Temperaturausgleich - Körper - Temperaturen - Mischen - Temperaturänderung - Gleichgewichtstemperatur - Dichteänderung - Spezifische Wärmekapazität - Spez. Wärmekapazität - Mischungstemperatur - Herleitung - Beweis - Absolute Temperatur - Thermodynamische Temperatur - Grundgleichung der Wärmelehre - Wärmeleitung - Konduktion - Wärmemenge - Wärmewiderstand - Wärmeleitwert - Konvektion - Festkörper - Ausdehnung - Wärmeübertragung - Wärmetransport - Wärmeenergie - Wärmestrom - Wärmefluss - Wärmeausdehnung - Thermische Ausdehnung - Thermische Expansion - Thermische Längenausdehnung - Dehnung - Wärmedehnung - Thermische Dehnung - Nullpunkt - Wärmeleiter - Wärmeleitfähigkeit - Wärmeströmung - Wärmedurchgang - Wärmeübergang - Wärmedurchgangskoeffizient - Wärmeübergangskoeffizient - Wärmedurchgangswiderstand - Wärmedurchlass - Wärmedurchlasskoeffizient - Wärmedurchlasswiderstand - Thermischer Ausdehnungskoeffizient - Thermischer Leitwert - Thermischer Widerstand - Thermische Leitfähigkeit - Thermisches Verhalten - Fluid - Fluide - Einheit - Eigenschaften - Material - Leiter - Gesetzmäßigkeiten - Wärmekapazitäten - Wärmeinhalt - Begriff - Begriffe - Spezifische Wärme - Newtonsches Abkühlungsgesetz - Abkühlungsgesetz - Grundlagen - Was - Wie - Weshalb - Was ist - Warum - Bedeutung - Was bedeutet - Einführung - Erklärung - Einfach erklärt - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Formel - Formelzeichen - Stoffe - Tabelle - Liste - Einheiten - Wasser - Alkohol - Physikalische Einheiten - Berechnung - Ausdehnung - Ausdehnung von Flüssigkeiten - Ausdehnung von Feststoffen - Grundlagen - Formeln - Gas - Gase - Längenausdehnung - Flächenausdehnung - Volumenausdehnung - Koeffizient - Ausdehnungskoeffizient - Längenausdehnungskoeffizient - Ausdehnungskoeffizienten - Wärmeausdehnungskoeffizient - Wärmeübergangszahl - Wärmeübertragungskoeffizient - Wärmemitführung - Wärmeübergangswiderstand - Raumausdehnungskoeffizient - Raumausdehnung - Temperaturkoeffizient - Temperaturleitfähigkeit - Temperaturbeiwert - Temperaturleitzahl - Dehnung - Erwärmung - Ausdehnung bei Erwärmung - Länge - Fläche - Wand - Wände - Rohr - Rohrwand - Volumen - Volumenänderung - Längenänderung - Flächenänderung - Feststoffe - Festkörper - Volumenausdehnungskoeffizient - Instationäre Wärmeleitung - Stationäre Wärmeleitung - Wärmeleitfähigkeiten - Bauphysik - Flüssigkeit - Flüssigkeiten - Warm - Kalt - Heiß - Physik - Physikalisch - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Aufgaben - Rechner - Mischungsaufgabe - Mischungsaufgaben - Mischungsrechner - Wärmeleistung - Wärmekapazität - Thermische Energie - U-Wert - K-Wert - Wärmedämmwert - Verbrennung - Verbrennungsenergie - Verbrennungswärme - Heizwert - Spezifischer Heizwert - Heizwerttabelle - Thermische Leistung - Emissionsgrad - Brennwert - Oberer Heizwert - Unterer Heizwert - Brennstoff - Brennstoffe - Fester Brennstoff - Flüssiger Brennstoff - Gasförmiger Brennstoff - Wärmestrahlung - Strahlungsfluss - Absorption - Thermische Strahlung - Temperaturstrahlung - Wärmeabsorption - Absorptionsgrad - Transmissionsgrad - Reflexionsgrad - Emission - Formeln - Flüssigkeitsthermometer - Temperaturangaben - Temperaturmesser - Temperaturmessung - Temperaturmessungen - Thermometer - Celsius - Fahrenheit - Kelvin - Grad - Temperaturskala - Temperaturskalen - Bimetallthermometer - Thermometerarten - Gasdruckthermometer - Flüssigkeitsthermometer - Elektrische Thermometer - Digitale Thermometer - Umrechnen - Skala - Celsius Skala - Fahrenheit Skala - Kelvin Skala - Skalen - Funktion - Bimetall - Bimetalle - Bimetallschalter - Bimetallstreifen - Bimetallthermometer

   

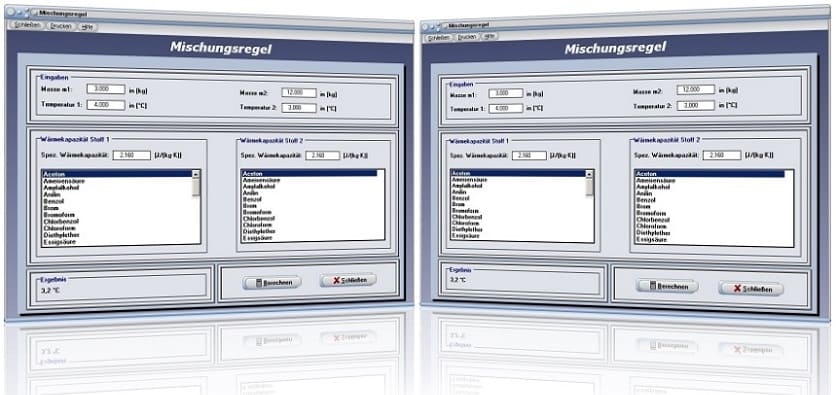
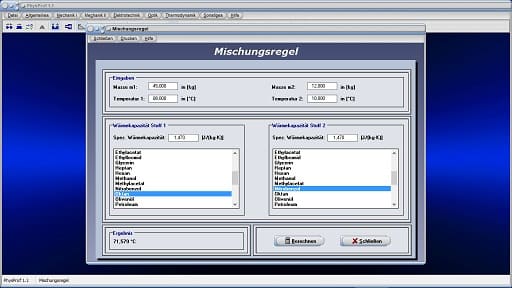
Modul Mischungsregel

---

Im kleinen Unterprogramm [Thermodynamik] - [Mischungsregel] können Berechnungen zum Wärmeaustausch zweier Körper nach der Richmannschen Mischungsregel durchgeführt werden.
 

Mischungsregel - Abbildung 1
 

Mischungsregel - Abbildung 2
 

Die Wärmelehre (Thermodynamik) ist ein naturwissenschaftliches Fachgebiet, welches sich mit Zustandsänderungen von Festkörpern, Flüssigkeiten und Gasen auseinandersetzt. Sie basiert auf der Mechanik und behandelt unter anderem die Zufuhr und die Abgabe von Wärme, sowie thermische Energieumwandlungen.
    

Mischung - Mischungsregel - Richmannsche Mischungsregel

 
Als Mischung wird ein Gemenge verschiedener chemischer Stoffe bezeichnet. Werden zwei oder mehrere Körper unterschiedlicher Temperatur miteinander in Berührung gebracht, so erfolgt ein Wärmeaustausch. Der Körper der die höhere Temperatur besitzt gibt Wärme ab und der Körper der über die niedrigere Temperatur verfügt nimmt Wärme auf. Die Temperaturdifferenz geht gegen Null und es wird von Wärmemischung (Temperaturausgleich) gesprochen.
 
Nach dem Gesetz von der Erhaltung der Energie gibt der Körper, welcher eine höhere Temperatur besitzt, soviel Wärmemenge ab, wie der Körper niederer Temperatur aufnimmt. Die gemeinsame Temperatur (Mischungstemperatur oder Mischtemperatur) zweier Körper oder Fluide kann gemäß der geltenden Mischungsregel wie folgt bestimmt werden:
 

 

Diese Formel wird als Richmannsche Mischungsregel bezeichnet. Sie nach ihrem Entdecker Georg Wilhelm Richmann (1711 - 1753) benannt. Die Anwendung dieser Mischungsregel heißt Mischungsrechnung oder Mischungsrechnen.
 
Hierbei sind:

c_1,c₂: Spez. Wärmekapazitäten (thermische Kapazitäten) der Körper 1 und 2 [kJ/(kgK)]

m₁,m₂: Massen der Körper 1 und 2 [kg]

ϑ₁,ϑ₂: Temperaturen der Körper 1 und 2 vor deren Mischung [K]

ϑ_m: Gemeinsame Temperatur (Mischungstemperatur) beider Körper nach deren Mischung [K]
 

Die Summe der Wärmeinhalte vor deren Mischung ist gleich dem Gesamtwärmegehalt nach deren Mischung. Anhand dieses Zusammenhangs können entsprechende Mischungsaufgaben gelöst werden.
 

Programmbedienung

 
Um die Temperatur zweier Stoffe ermitteln zu lassen, die diese nach deren Mischung besitzen, geben Sie in die dafür vorgesehenen Eingabefelder die entsprechenden Werte für die Temperatur und Masse des jeweiligen Stoffes ein.

Sind die spezifischen Wärmekapazitäten der zu mischenden Stoffe bekannt, so geben Sie deren Werte in die dafür vorgesehenen Felder ein. Möchten Sie die Berechnung mit einem in der Liste aufgeführten Stoff durchführen lassen, so klicken Sie den entsprechenden Listeneintrag an. Hierauf übernimmt das Programm den Wert für den selektierten Stoff in das dafür zur Verfügung stehende Eingabefeld.

Nach der Bedienung der Schaltfläche Berechnen wird die Mischungstemperatur der beiden Stoffe in °C ausgegeben.

 

Erwärmungsgesetz

 
Das Erwärmungsgesetz besagt: Um einen Körper, der die Masse m besitzt und aus einem Material mit der spezifischen Wärmekapazität c besteht, von der Temperatur ϑ₁ auf eine Temperatur ϑ₂ zu erwärmen, ist seine Wärmeenergie um den Betrag ΔE_th = c · m · (ϑ₂ – ϑ₁) zu erhöhen.
 
Dies kann durch die Zufuhr der entsprechend erforderlichen Wärmemenge W_Q durchgeführt werden. Es gilt:

W_Q = c · m · (ϑ₂ – ϑ₁)

c: spez. Wärmekapazität (thermische Kapazität) des Körpers [kJ/(kgK)]
m: Masse des Körpers [kg]
ϑ₁,ϑ₂: Temperaturen des Körpers [K]
W_Q: zuzuführende Wärmemenge [J]

Als Gleichgewichtstemperatur wird diejenige Temperatur angegeben, die sich nach ausreichend langer Zeit in einem System ohne externes Eingreifen einstellt.
 

Newtonsches Abkühlungsgesetz

 
Das Newtonsche Abkühlungsgesetz besagt, dass sich die momentane Änderungsrate der Temperatur eines Körpers (einer Flüssigkeit) proportional zur Differenz zwischen der Temperatur des abkühlenden Körpers zur Zeit t und der Umgebungstemperatur verhält. Es gilt:

T(t) = (T₀ - T_U)e^-kt + T_U

Die Wärmeverlustrate eines Körpers ist somit direkt proportional zur Temperaturdifferenz zwischen ihm und seiner Umgebung.

T(t): Temperatur des Körpers zur Zeit t [°C]
t: Zeit in Minuten [min]
T_U: Umgebungstemperatur [°C]
T₀:  Temperatur des Körpers zum Zeitpunkt t = 0 [°C]
k: Proportionalitätsfaktor (Abkühlungsfaktor) [1/min]
 

Thermometer - Temperatur - Kelvin - Celsius - Fahrenheit - Temperaturskala - Temperaturmesser

 
Die Temperatur ist ein Maß dafür, wie kalt oder warm ein Körper, eine Flüssigkeit oder ein Gas ist. Sie ist eine Zustandsgröße und bildet ein Maß für die Bewegungsenergie von Molekülen. Sie kennzeichnet den thermischen Zustand eines Körpers oder eines Systems und beschreibt den messbaren Wärmezustand von Materie.

Als Temperaturdifferenz oder Temperaturunterschied wird der Unterschied der Temperaturen zweier Messpunkte ΔT verstanden, die in der Zeit oder ihrer Position differieren. Sie wird in Kelvin (K) angegeben.

Temperaturskalen: Bei einer Temperaturskala handelt es sich um eine in Graden definierte Skala, die gleichmäßig untergliedert ist und zur Anzeige von Temperaturen Verwendung findet.
 
 


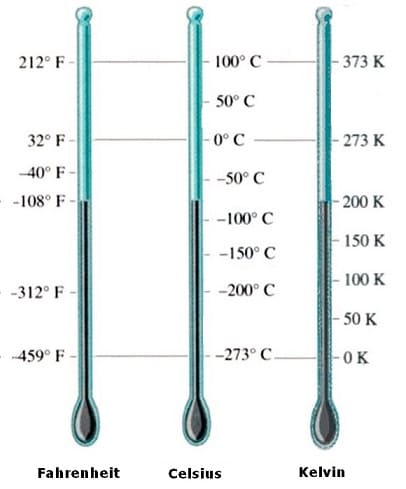
Erfasst werden Temperaturen mit Hilfe von einem Thermometer einem Temperaturmesser. Diese Erfassung wird als Temperaturmessung bezeichnet. Die SI-Einheit der Temperatur ist das Kelvin [K]. Zudem finden die Einheiten Fahrenheit [F] sowie Celsius [°C] Anwendung. Die Kelvin-Skala hat ihren Nullpunkt beim theoretischen Nullpunkt (absoluten Nullpunkt). Der Nullpunkt der Celsius-Skala liegt bei 273,15 K. Sie besitzt diesen beim Erstarrungspunkt des Wassers. Die Temperaturdifferenz dieser beiden Skalen beträgt somit 273,15 K.

Bei einem Flüssigkeitsthermometer handelt es sich um ein Steigrohr, welches über einen unten angeordneten Vorratsbehälter für eine Flüssigkeit verfügt. Erfolgt eine Erwärmung derer, so dehnt sich diese Flüssigkeit aus und es erfolgt ein Anstieg derer im Steigrohr. An einer dafür konzipierten Skala lässt sich an diesem Steigrohr die vorhandene Temperatur ablesen.

Fahrenheit, Celsius, Kelvin, Reaum - Skala:
 
Es existieren verschiedene Temperaturskalen. Sie alle sind nach bedeutenden Wissenschaftlern benannt, die sie entwickelt und eingeführt haben. Es handelt sich um die Fahrenheit Skala, die Celsius Skala, die Kelvin Skala sowie die Reaum Skala. Bei den meist eingesetzten Skalen handelt es sich um die Skalen von Fahrenheit (USA), Celsius und Kelvin (Physik).

Die Fahrenheit Skala wurde vom Danziger Glasbläser David Fahrenheit um 1715 entwickelt. Als Nullpunkt wurde von ihm die tiefste Temperatur des besonders kalten Winters inh Danzig (im jahr 1709) gewählt. Der obere Fixpunkt wurde von ihm willkürlich mit dem Wert 100 festgelegt.

Der schwedische Astronom Anders Celsius stellte im Jahr 1742 eine einfacher handzuhabende Skalierung vor. Sie trägt die Bezeichnung Celsius Skala. Als ersten Fixpunkt legte er die Schmelztemperatur (Gefriertemperatur) von Wasser (0° C) fest und als zweiten Fixpunkt wählte er die Siedetemperatur des Wassers (100  C).

Beide der zuvor beschriebenen Skalen, besitzen frei festgelegte Fixpunkte und sie können sowohl positive wie auch negative Temperaturwerte besitzen.

Die absolute Temperatur (thermodynamische Temperatur) ist eine Temperaturskala, die sich auf den physikalisch festgelegten absoluten Nullpunkt (- 273,15 °C oder 0 K) bezieht. Dieser Punkt ist der untere Fixpunkt der Kelvin Skala. Bei dieser Temperatur handelt es sich um den absoluten Nullpunkt, unterhalb dessen keine Temperatur möglich ist. Es handelt sich um die Temperatur bei welcher die kinetische Energie der Teilchen eines Systems gleich dem Wert Null wäre.
 
Die Umrechnung zwischen Temperaturangaben der Maßeinheiten Celsius und Kelvin, kann wie folgt durchgeführt werden:

Temperaturumrechnung von Celsius in Kelvin:



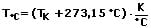
Temperatur umrechnnen von Kelvin in Celsius:



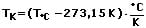
Eine Umrechnung von Temperaturangaben zwischen den Maßeinheiten Celsius und Fahrenheit kann gemäß der nachfolgend gezeigten Methoden erfolgen:

Umrechnung von Celsius in Fahrenheit:



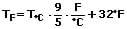
Umrechnung von Fahrenheit in Celsius:


 
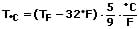
Thermometerarten:

Ein Thermometer ist ein Messgerät zur Bestimmung einer Temperatur. Es existiert eine Vielzahl verschiedener Thermometerarten in unterschiedlichen Bauformen. Nachfolgend wird auf einige der am häufigsten eingesetzten Arten eingegangen. Hierzu zählen unter anderem:

- Bimetallthermometer: Genutzt wird die unterschiedliche Wärmeausdehnung zweier Metalle.
- Gasdruckthermometer: Genutzt wird die Druckänderung eines Gases bei Temperaturänderungen.
- Flüssigkeitsthermometer: Genutzt wird die thermische Ausdehnung von Flüssigkeiten (z.B. Quecksilberthermometer).
- Elektrische Thermometer (digitale Thermometer): Genutzt werden temperaturabhängige elektrische Eigenschaften von Materialien.
 

 
Der Begriff Dehnung beschreibt die räumliche Vergrößerung eines Körpers unter dem Einfluss von Kräften oder Temperaturänderungen. Als Wärmeausdehnung, Wärmedehnung, thermische Ausdehnung oder thermische Expansion wird die Änderung der geometrischen Abmessungen eines Körpers bezeichnet, die durch eine Veränderung seiner Temperatur hervorgerufen wird.
 
Mit dem Ausdehnungskoeffizient oder Wärmeausdehnungskoeffizient (thermischer Ausdehnungskoeffizient) wird ein Kennwert beschrieben, welcher das Verhalten eines Stoffes bezüglich der Veränderungen seiner Abmessungen bei Temperaturveränderungen beschreibt. Er untergliedert sich in den Längenausdehnungskoeffizient und den Volumenausdehnungskoeffizient (Raumausdehnungskoeffizient) und besitzt die Einheit 1/K.


I - Ausdehnung (Wärmeausdehnung - Thermische Ausdehnung - Thermische Expansion) fester Körper

Bei der Erwärmung von Körpern vergrößert sich der Abstand zwischen den Molekülen und sie nehmen einen größeren Raum ein. Sie dehnen sich in alle Richtungen aus. Handelt es sich um längliche Körper, so wirkt sich deren Ausdehnung maßgeblich auf deren Länge aus. Der Längenausdehnungskoeffizient fester Körper α bildet sich aus dem Quotienten der relativen Längenänderung Δl/l₁ sowie der Temperaturänderung Δt.

Der Längenausdehnungskoeffizient ist wie folgt definiert:

α =  Δl/(l₁·Δt)

I-1: Längenausdehnung fester Körper:

Die Längenänderung bzw. thermische Längenausdehnung eines Körpers kann näherungsweise wie folgt bestimmt werden:

Δl = l₁·α·Δt

Es gilt:

l₂ = l₁·(1+α·Δt)

l₁: Anfangslänge [m]
l₂: Endlänge [m]
α : Längenausdehnungskoeffizient [1/K]
Δl: Längenänderung (l₂-l₁) [m]
Δt: Temperaturänderung (t₂-t₁) [K]
 

I-2: Flächenausdehnung fester Körper:

Die Flächenänderung bzw. Flächenausdehnung eines Körpers bedeutet eine Längenänderung in zwei Dimensionen und kann näherungsweise bestimmt werden mit:

ΔA = A₁·2α·Δt

Es gilt:

A₂ = A₁·(1+2α·Δt)

A₁: Anfangsfläche [m²]
A₂: Endfläche [m²]
α : Längenausdehnungskoeffizient [1/K]
Δl: Flächenänderung (A₂-A₁) [m²]
Δt: Temperaturänderung (t₂-t₁) [K]


I-3: Volumenausdehnung fester Körper:

Die Volumenänderung bzw. Volumenausdehnung eines Körpers bedeutet eine Längenänderung in drei Dimensionen und kann näherungsweise bestimmt werden mit:

ΔV = V₁·3α·Δt

Es gilt:

V₂ = V₁·(1+3α·Δt)

V₁: Anfangsvolumen des Körpers [m³]
V₂: Endvolumen des Körpers [m³]
α : Längenausdehnungskoeffizient [1/K]
Δl: Volumenänderung des Körpers (V₂-V₁) [m³]
Δt: Temperaturänderung des Körpers (t₂-t₁) [K]


II - Ausdehnung (Wärmeausdehnung - Thermische Ausdehnung - Thermische Expansion) von Flüssigkeiten:

Bei der Erwärmung von Flüssigkeiten vergrößert sich der Abstand zwischen den Molekülen ebenso wie bei Körpern und sie nehmen einen größeren Raum ein. Sie dehnen sich ebenfalls in allen Richtungen aus. Ihre Ausdehnung ist jedoch wesentlich erheblicher wie bei festen Körpern. Wasser bildet hinsichtlich dessen eine Ausnahme, denn sein Volumenänderungsverhalten ist abhängig von seiner Temperatur veränderlich. Der Volumenausdehnungskoeffizient γ bildet sich aus dem Quotienten der relativen Volumenänderung ΔV/V₁ sowie der Temperaturänderung Δt.

Der Volumenausdehnungskoeffizient einer Flüssigkeit ist wie folgt definiert:

γ =  ΔV/(V₁·Δt)

Die Volumenänderung einer Flüssigkeit kann näherungsweise wie folgt bestimmt werden:
 
ΔV = V₁·γ·Δt

Es gilt:

V₂ = V₁·(1+γ·Δt)
 
V₁: Anfangsvolumen der Flüssigkeit [m³]
V₂: Endvolumen der Flüssigkeit [m³]
γ: Volumenausdehnungskoeffizient [1/K]
ΔV: Volumenänderung der Flüssigleit (V₂-V₁) [m³]
Δt: Temperaturänderung (t₂-t₁) [K]
 

III - Dichteänderung von Flüssigkeiten:
 
Flüssigkeiten ändern durch Wärmezufuhr ihre Dichte sowie ihr Volumen. Dieser Vorgang wird als Dichteänderung bezeichnet. Hierbei gilt die nachfolgende Gesetzmäßigkeit:

ρ₂ = ρ₁/(1+γ·Δt)

ρ₁: Anfangsdichte der Flüssigkeit [kg/m³]
ρ₂: Enddichte der Flüssigkeit [kg/m³]
γ: Volumenausdehnungskoeffizient [1/K]
Δt: Temperaturänderung (t₂-t₁) [K]
 

IV - Ausdehnung von Gasen:

Bei der Erwärmung von Gasen vergrößert sich der Abstand zwischen den Molekülen ebenso wie bei Körpern und Flüssigkeiten und sie nehmen einen größeren Raum ein. Sie dehnen sich in allen Richtungen aus. Ihre Ausdehnung ist jedoch wesentlich erheblicher wie bei festen Körpern oder Flüssigkeiten. Der Volumenausdehnungskoeffizient γ eines Gases bildet sich aus dem Quotienten der relativen Volumenänderung ΔV/V₀ sowie der Temperatur t.

Der Volumenausdehnungskoeffizient eines Gases ist wie folgt definiert:

γ =  ΔV/(V₀·t)

Da dieser bei idealen Gasen annähernd gleich ist,gilt:
 
γ =  1/(273,15 K) = 0,003661 1/K
 
Die Volumenänderung eines Gases kann näherungsweise wie folgt bestimmt werden:
 
V_t = V₀·(1+γ·t)
 
V_t: Volumen des Gases bei einer Temperatur t [m³]
V₀: Volumen des Gases bei 0°C [m³]
γ: Volumenausdehnungskoeffizient [1/K]
t: Temperatur bei welcher das Gas das Volumen V_t besitzt [K]
 

 
Die Wärmeleitfähigkeit (thermische Leitfähigkeit) eines Stoffes ist eine Konstante dessen. Gute Wärmeleiter sind Metalle. Kunststoffe sowie Glas und Holz hingegen sind schlechte Wärmeleiter. Einige dieser Materialien mit geringer Wärmeleitfähigkeit dienen als Dämmstoffe.

Unter Wärmeübertragung oder Wärmetransport wird die Übertragung thermischer Energie verstanden, welche über verschiedene Stellen (Grenzen) erfolgt. Hierbei wird zwischen den drei Vorgängen Wärmeströmung (Konvektion), mechanischer Berührung und dem Mitführen thermischer Energie (Wärmeleitung) unterschieden.


 
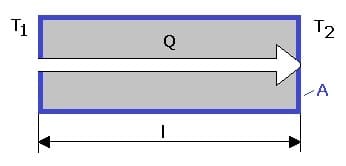
Als Konvektion (Wärmemitführung) wird das Transportieren von Wärmeenergie bezeichnet, welches durch die Strömung eines Mediums verursacht wird. Bei der Wärmeleitung (Konduktion) hingegen erfolgt das Weiterleiten (Übertragen) der Wärmeenergie innerhalb eines Körpers. Die hierbei transportierte Wärmemenge kann wie folgt berechnet werden:


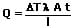
Q: Übertragene Wärmemenge [J]
t: Dauer der Wärmeübertragung [s]
A: Leiterquerschnitt [m²]
ΔT: Temperaturunterschied (Temperaturdifferenz) zwischen Anfang und Ende des Leiters [K]
λ: Wärmeleitfähigkeit des Leiters [W/(m·K)]
l: Länge des Wärmeleiters [m]

Instationäre Wärmeleitung:

Als instationäre Wärmeleitung wird der Prozess bezeichnet, bei dem eine zeitabhängige Temperaturveränderung zwischen zwei sich berührenden Körpern erfolgt. Zwei miteinander in Kontakt stehende Medien verändern hierbei ihre Temperaturen.

Stationäre Wärmeleitung:

Bleibt ein zwischen zwei Körpern bestehender Temperaturunterschied zeitlich und lokal unverändert, so wird von einer stationären Wärmeleitung gesprochen. Die Temperaturen einzelner sich berührender Medien bleiben konstant.
 
Als Wärmestrom oder Wärmefluss wird die in der Zeit t übertragene Wärmeenergie bezeichnet. Es gilt:

Φ = Q/t

Φ: Wärmestrom (Wärmefluss) [J/s]
Q: Übertragene Wärmemenge [J]
t: Dauer der Wärmeübertragung [s]


Der Wärmewiderstand (thermischer Widerstand) R_th ist ein Maß für die Temperaturdifferenz, die in einem Medium beim Passieren eines Wärmestroms entsteht. Für diesen Kennwert gilt:


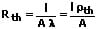
R_th: Wärmewiderstand [K/W]
l: Länge des Leiters [m]
A: Querschnittsfläche des Leiters [m²]
λ: Wärmeleitfähigkeit des Leiters [W/(m·K)]
ρ_th: Spezifischer Wärmewiderstand [(m·K)/W]

Der Wärmeleitwert (thermischer Leitwert) λ_th ist der Kehrwert des Wärmewiderstands des Mediums. Er ist wie folgt definiert:


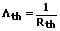
Bei der Bezeichnung Temperaturkoeffizient (Temperaturbeiwert) handelt es sich um Materialkonstante, die die relative Änderung der Temperatur gegenüber einer festgelegten Bezugstemperatur (Referenztemperatur) beschreibt.
 
Mit der Temperaturleitfähigkeit (Temperaturleitzahl) wird eine Materialeigenschaft beschrieben, welche die zeitliche Ausbreitung der Temperatur (Temperaturänderung) aufgrund der in einem Material vorhandenen Wärmeleitung widergibt. Es gilt:

a = λ/(ρ·c)

a: Temperaturleitfähigkeit des Materials [m²/s]
λ: Wärmeleitfähigkeit des Materials [W/(m·K)]
ρ: Dichte des Materials [kg/m³]
c: Spezifische Wärmekapazität (spezifische Wärme) des Materials [kJ/(kgK)]

Eine Wärmeabsorption findet statt, wenn ein Körper eine niedrigere Temperatur als seine Umgebung besitzt. Sie dauert an bis ein Temperaturausgleich zwischen dem Körper und seiner Umgebung stattgefunden hat.
 

 
Nachfolgend Beschriebenes findet unter anderem in der Bauphysik Anwendung.

I - Wärmeübergang:




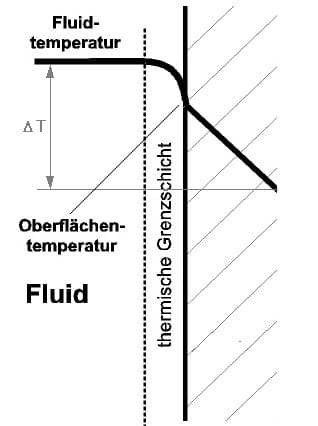
Als Wärmeübergang wird der Vorgang der Wärmeübertragung zwischen der Oberfläche eines Festkörpers und einem Fluid oder einem Gas bezeichnet. Fluiden werden in der Physik Gase und Flüssigkeiten zugeordnet. Bei einem derartigen Vorgang (Wärmeübergang) gilt:

Q = α·ΔT·A·t

Q: Durch die Grenzfläche tretende Wärmemenge [J]
α: Wärmeübergangskoeffizient [W/(m²·K)]
ΔT: Temparaturunterschied (Temperaturdifferenz) zwischen Oberfläche und angrenzendem Medium [K]
A: Übergangsfläche [m²]
t: Dauer des Wärmeübergangs [s]

II - Wärmedurchgang:

Als Wärmedurchgang wird der Vorgang der Wärmeübertragung von einem flüssigen oder gasförmigen Fluid durch eine Wand (einen Festkörper) auf ein anderes Fluid bezeichnet. Dieser umfasst die nachfolgend aufgeführten drei Vorgänge:

 - Wärmeübergang von Fluid 1 an die Oberfläche der Wand
 - Wärmeleitung durch die Wand
 - Wärmeübergang von der Oberfläche der Wand auf Fluid 2




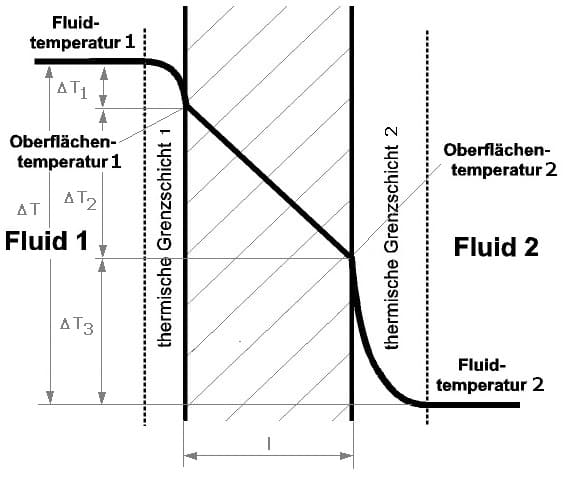
Es treten in diesem Fall drei Temperaturdifferenzen zwischen den Fluiden und den Medien auf. Diese setzen sich wie in der obigen Abbildung dargestellt zusammen. ΔT = ΔT₁ + ΔT₂ + ΔT₃.

Für den Wärmedurchgangskoeffizienten k gilt:


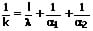
k: Wärmedurchgangskoeffizient [W/(m²·K)]
l: Wanddicke des Festkörpers [m]
α₁: Wärmeübergangskoeffizient der Grenzfläche 1 [W/(m²·K)]
α₂: Wärmeübergangskoeffizient der Grenzfläche 2 [W/(m²·K)]
λ: Wärmeleitfähigkeit des Festkörpers [W/(m·K)]

Bei einem deratigen Vorgang gilt für den Wärmedurchgang Q:

Q = k·ΔT·A·t

Q: Durch die Grenzflächen (Wand) tretende Wärmemenge [J]
k: Wärmedurchgangskoeffizient [W/(m²·K)]
ΔT: Temparaturunterschied zwischen Oberfläche und angrenzendem Medium [K]
A: Übergangsfläche [m²]
t: Dauer des Wärmeübergangs[s]
 

Der Wärmedurchgangskoeffizient (U-Wert oder k-Wert, auch als Wärmedämmwert bezeichnet) k beschreibt die spezifische Wärmeleitfähigkeit eines Bauteils. Er gibt Auskunft über die Wärmemenge die im Zeitraum von einer Sekunde über eine Fläche von 1 m² durch eine Trennwand zwischen zwei Räumen hindurchgelassen wird, wenn der Unterschied zwischen den beiderseits herrschenden Temperaturen 1 K beträgt.

Je niedriger der Wärmedurchgangskoeffizient ist, desto höher ist die Wärmedämmung des entsprechenden Materials. Der Kehrwert des Wärmedurchgangskoeffizienten wird als Wärmedurchgangswiderstand R_T bezeichnet.

Der Wärmeübergangskoeffizient (auch als Wärmeübergangszahl oder Wärmeübertragungskoeffizient bezeichnet) ist eine Kennzahl, die die Intensität des Wärmeübergangs an einer Grenzfläche bestimmt. Er beschreibt die Fähigkeit einer Flüssigkeit oder eines Gases, Energie von der Oberfläche eines Stoffes abzuführen bzw. an diese abzugeben.
 
Der Wärmedurchgangswiderstand R_T ist wie folgt definiert:

R_T = 1/(k·A)

R_T: Wärmedurchgangswiderstand [1/K]
k: Wärmedurchgangskoeffizient [W/(m²·K)]
A: Übergangsfläche [m²]

Wärmedurchgangskoeffizient bei mehreren Schichten:

1. Wand mit mehreren Schichten


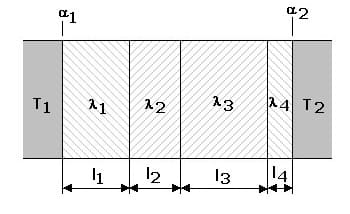
Für den Wärmedurchgangskoeffizienten ebener Wände mit mehreren Schichten gilt:


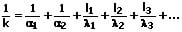
k: Wärmedurchgangskoeffizient [W/(m²·K)]
l₁,l₂,l₃..: Wanddicke einzelner Schichten [m]
α₁: Wärmeübergangskoeffizient der Grenzfläche 1 [W/(m²·K)]
α₂: Wärmeübergangskoeffizient der Grenzfläche 2 [W/(m²·K)]
λ₁,λ₂,λ₃: Wärmeleitfähigkeit einzelner Schichten [W/(m·K)]

2. Rohrwand


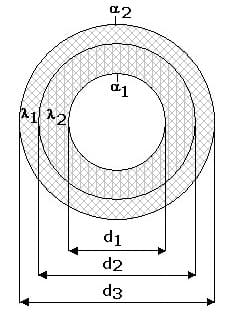
Der Wärmedurchgangskoeffizient einer Rohrwand mit einer Schicht kann wie folgt berechnet werden:


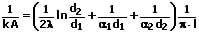
Der Wärmedurchgangskoeffizient einer Rohrwand mit mehreren Schichten berechnet sich wie nachfolgend gezeigt:


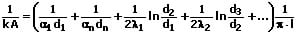
k: Wärmedurchgangskoeffizient [W/(m²·K)]
l: Rohrlänge [m]
d₁,d₂,d₃..: Durchmesser der Rohre (von innen nach außen) [m]
α₁: Wärmeübergangskoeffizient der Grenzfläche 1 [W/(m²·K)]
α₂: Wärmeübergangskoeffizient der Grenzfläche 2 [W/(m²·K)]
λ₁,λ₂,λ₃: Wärmeleitfähigkeit einzelner Schichten [W/(m·K)]

 
Als Wärmeübergangswiderstand R_s wird der Widerstand bezeichnet, den eine Grenzschicht oder Oberfläche des umgebenden Mediums zum Bauteil dem Wärmestrom entgegensetzt. Für ihn gilt:

R_s = 1/h = 1/(h_r+h_c)

R_s: Wärmeübergangswiderstand [W/(m²·K)]
h:  Wärmeübergangskoeffizient [m²·K/W]
h_r: Wärmeübergangskoeffizient der Strahlung [m²·K/W]
h_c:  Wärmeübergangskoeffizient der Konvektion [m²·K/W]


Der Wärmedurchlasswiderstand beschreibt das Verhältnis der Dicke eines Bauteils zu dessen Wärmeleitfähigkeit. Für ihn gilt bei einer einzelnen Schicht:

R = d/λ

und bei mehreren Schichten:

R = d₁/λ₁ + d₂/λ₂ + d₃/λ₃ ....

Der Wärmedurchlasskoeffizient ist der Kehrwert des Wärmedurchlasswiderstands. Er ergibt sich aus der Wärmeleitfähigkeit des entsprechenden Stoffs dividiert durch die Schichtdicke des Materials.

Λ = 1/R = λ/d

R: Wärmedurchlasswiderstand [W/(m²·K)]
Λ: Wärmedurchlasskoeffizient [(m²·K)/W]
λ,λ₁,λ₂,λ₃: Wärmeleitfähigkeit  (Wärmeleitzahl) [W/(m·K)]
d,d₁,d₂,d₃: Schichtdicke des Materials [m]
   
 

 
Wärmeenergie:

Wärmeenergie (thermische Energie) ist einer spezielle Form der Energie, welche das innere Wärmepotenzial eines Stoffes beschreibt. Sie ist eine Zustandsgröße und ist, wie alle anderen Energiearten, in andere konvertierbar. Um die den Aggregatzustand oder die Temperatur eines Körpers zu verändern, ist sie zuzuführen oder abzugeben. Ihre SI-Einheit ist das Joule [J] bzw. das Newtonmeter [Nm].

Wärmemenge:

Unter Wärme oder Wärmemenge wird die Energie verstanden, die zwischen zwei Systemen (Körpern) aufgrund ihrer unterschiedlichen Temperaturen zum Austausch kommt. Für die zur Erwärmung eines Körpers erforderliche Wärmeenergie gilt (Grundgleichung der Wärmelehre):

Q = c·m·Δt

Q: Wärmemenge [J]
c: Spezifische Wärmekapazität des Stoffes der zu erwärmen ist [J/(kg·K)]
m: Masse des zu erwärmenden Körpers [kg]
Δt: Differenz der Temperaturen, die durch die Wärmemenge Q erzeugt wird [K]

Wärmeinhalt:

Unter Wärmeinhalt wird die auf 0 °C bezogene thermische Energie verstanden, die ein Körper bei einer bestimmten Temperatur besitzt. Es gilt:

Q_i = c·m·t

Q_i: Wärmeinhalt des Körpers [J]
c: Spezifische Wärmekapazität des Stoffes [J/(kg·K)]
m: Masse des Körpers [kg]
t: Temperatur die der Körper besitzt [°C]
 
Spezifische Wärmekapazität (spezifische Wärme) eines Stoffes:

Definition 1:
 
Die spezifische Wärmekapazität (spez. Wärmekapazität) eines Stoffes ist das Verhältnis seiner Wärmekapazität bezogenen auf seine Masse. Es gilt:

c = C/m

c: spezifische Wärmekapazität des Stoffes [J/(kg·K)]
C: Wärmekapazität des Stoffes [J/K]
m: Masse des Stoffes [kg]

Definition 2:
 
Unter der spezifischen Wärmekapazität eines Stoffes wird die Wärmemenge verstanden, die durch die entsprechende Erhöhung oder Absenkung der Temperatur (Temperaturdifferenz ) sowie die Masse des Stoffes geteilt wird.

c = Q/(m·ΔT)

c: spezifische Wärmekapazität des Stoffes [J/(kg·K)]
Q: zugeführte Wärmemenge [J]
m: Masse des Stoffes [kg]
ΔT: Temperaturdifferenz [K]

Liegt ein Stoffgemsich vor, so gilt für die spezifische Wärmekapazität dessen:


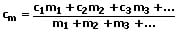
c_m: spezifische Wärmekapazität des Stoffgemischs [J/(kg·K)]
c₁,c₂,c₃ ...: spezifischen Wärmekapazitäten einzelner Stoffe [J/(kg·K)]
m: Massen einzelner Stoffe [kg]

Wärmekapazität eines Körpers:

Die Wärmekapazität C eines Körpers ist das Verhältnis der ihm zugeführten Wärme Q zur damit erzielten Temperaturerhöhung. Sie entspricht der Wärmemenge, welche zum Erwärmen eines homogenen Körpers um 1 K erforderlich ist. Es gilt:

C = Q/ΔT

C: Wärmekapazität des homogenen Körpers [J/K]
Q: Wärmeinhalt des homogenen Körpers [J]
ΔT: Temperaturerhöhung [K]

und:

C = c·m

C: Wärmekapazität des homogenen Körpers [J/K]
c: spezifischer Wärmeinhalt des Stoffes [J/(kg·K)]
m: Masse des Körpers [kg]
 
Thermische Leistung:

Als thermische Leistung (Wärmeleistung) wird eine physikalische Größe bezeichnet, die die innerhalb eines Zeitraums umgesetzte Wärmeenergie angibt. Es gilt:

P = Q/t

P: Thermische Leistung [W]
Q: Umgesetzte Wärmeenergie [J]
t: Zeitraum [s]
 

 
Der spezifische Heizwert H_u (die Verbrennungswärme, früher unterer Heizwert) eines flüssigen oder festen Stoffes ist die Relation der bei einer Verbrennung dessen frei werdenden Energie zu seiner Masse. Es gilt:

H_u = Q/m

H_u: spezifischer Heizwert des zu verbrennenden Stoffes [J/kg]
Q: frei werdende Menge an Wärmenergie [J]
m: Masse des zu verbrennenden Stoffes [kg]

Der spezifische Heizwert H' (die Verbrennungswärme, früher unterer Heizwert) eines gasförmigen Stoffes berechnet sich wie folgt:

H_u' = Q/V_n

H_u': spezifischer Heizwert des zu verbrennenden Gases [J/m³]
Q: freiwerdende Menge an Wärmenergie [J]
V_n: Normvolumen des zu verbrennenden Gases [m³]

Dieser Wert bezieht sich auf das Normvolumen des Gases bei 0 K und einen Druck von p_n = 101325 Pa.

Mit dem Heizwert H_i (früher unterer Heizwert _Hu) wird die Energiemenge eines Stoffes beschrieben, die durch Verbrennen in Form von Wärme nutzbar gemacht werden kann.

Der Brennwert H_s (früher oberer Heizwert H_o) beschreibt die Verbrennungsenergie sowie die Energie, die bei der Kondensation des im Abgas involvierten Wasserdampfs freigesetzt wird und ist ein Maß für die spezifisch je Bemessungseinheit in einem Stoff enthaltene thermische Energie.
 

 
Wärmestrahlung (thermische Strahlung, Temperaturstrahlung) ist elektromagnetische Strahlung, die von einem Körper zu einem anderen transportiert wird. Die geschieht in Form von Emission oder Absorption.

1. Absorption

Ein Teil der Strahlung, die auf einen Körper trifft, wird von diesem absorbiert, reflektiert oder passiert ihn. Für den Absorptionsgrad, den Reflexionsgrad und den Transmissionsgrad gelten die nachfolgenden Definitionen,

Absorptionsgrad:

α = Φ_a/Φ₀

Reflexionsgrad:

ρ = Φ_r/Φ₀

Transmissionsgrad:

τ = Φ_t/Φ₀

Φ₀: Strahlungsleistung auftreffender Strahlung
Φ_a: Strahlungsleistung absorbierter Strahlung
Φ_r: Strahlungsleistung reflektierter Strahlung
Φ_t: Strahlungsleistung transmittierter Strahlung

2. Emission

Jeder Körper der eine andere Temperatur als 0 K besitzt, gibt Wärme ab. Diese Strahlung wird als Wärmestrahlung oder Temperaturstrahlung bezeichnet. Es ist dies die Strahlung die ein Körper abgibt, wenn sich seine Temperatur von 0°C unterscheidet.

Als Emissionsgrad eines Körpers wird eine Größe bezeichnet, die angibt, wie viel Strahlung dieser in Relation zu einem idealen Wärmestrahler (einem schwarzen Körper), abgibt. Sein Wert liegt zwischen 0 und 1. Schwarze Körper emittieren Strahlung am besten. Ihr Emissionsgrad wird auf den Wert 1 gesetzt.

Φ = εΦ_s

Φ: Strahlungsfluss der Strahlung eines nicht schwarzen Körpers (bei best. Temp)
ε: Emissionsgrad des nicht schwarzen Körpers
Φ_s: Strahlungsfluss der Strahlung des schwarzen Körpers (bei best. Temp)

Der zuvor beschriebene mathematische Zusammenhang besagt:

Die Strahlungsleistung die von einem beliebigen Körper ausgeht (der Strahlungfluss Φ) entspricht der des schwarzen Körpers (gleicher Temperatur), wenn dieser mit seinem eigenen Emissionsgrad ε multipliziert wird.
  

Mit dem Begriff Bimetall wird ein Metallstreifen bezeichnet, der aus zwei unterschiedlichen Metallen besteht, die übereinanderliegend stoffschlüssig (verschweißt) oder formschlüssig (verklebt oder vernietet) miteinander verbunden sind.



Bedingt durch die Tatsache, dass sich die beiden Metalle abhängig von einer auf sie einwirkenden Temperaturänderung unterschiedlich stark ausdehnen (die verwendeten Metalle besitzen eine unterschiedliche Längenausdehnung), verbiegt sich dieser Streifen.

Bimetalle werden zur Steuerung, wie auch zur temperaturabhängigen Betätigung von Ventilen sowie zur Auslösung von Schaltvorgängen verwendet. Mitunter kommen sie auch in Messinstrumenten zum Einsatz. Vornehmlich finden sie jedoch bei Bügeleisen, Kaffeemaschinen, Wasserkochern und Toastern etc. Anwendung.

Bimetallstreifen finden Einsatz bei Bimetallschaltern. Diese verfügen über einen festen Kontakt sowie einen Kontakt am Streifen. Bei Raumtemperatur befindet sich der Bimetallschalter beispielsweise in geschlossenem Zustand. Erhöht sich seine Temperatur, so wird der Stromfluss unterbrochen, da sich der Streifen verbiegt. Erniedrigt sich die Temperatur wieder, so kehrt der gebogene Metallstreifen in seine Ausgangslage zurück und schließt den elektrischen Kontakt wieder.
 
Bimetallthermometer bestehen aus zwei verschiedenen Metallstreifen, die unterschiedliche Wärmeausdehnungskoeffizienten besitzen. Bei einer Temperaturänderung dehnen sich beide Metalle unterschiedlich stark aus und bewirken damit eine Krümmung des Bimetalls. Aus der Stärke der Krümmung (bzw. des entsprechenden Winkels) kann über eine Skala die vorherrschende Temperatur abgelesen werden.
  

 
Nachfolgend aufgeführt ist eine Tabelle mit Angabe der spezifischen Wärmekapazitäten einiger Flüssigkeiten.
 

Flüssigkeit	Spez. Wärmekapazität in kJ/(kgK)
Aceton	2,16
Ameisensäure	2,15
Anilin	2,05
Benzol	1,725
Brom	0,46
Bromoform	0,54
Chlorbenzol	1,33
Chloroform	0,959
Diethylether	2,31
Essigsäure	2,052
Ethanol	2,43
Ethylacetat	1,922
Glycerin	2,39
Heptan	2,20
Hexan	2,253
Methanol	2,495
Methylacetat	2,14
Nitrobenzol	1,47
Oktan	21,186
Olivenöl	1,97
Petroleum	2,14
Pyridin	1,72
Quecksilber	0,139
Salpetersäure	1,72
Schwefelkohlenstoff	0,996
Schwefelsäure	1,38
Siliconöl	1,45
Terpentinöl	1,8
Tetrachlorkohlenstoff	0,861
Toluol	1,687
Trichlorethen	0,96
Wasser	4,182

 
  

 
In der nachfolgend angeordneten Tabelle sind die Längenausdehnungskoeffizienten (bei 20°C) einiger fester Stoffe aufgeführt.
 

Fester Stoff	Längenausdehnungs-koeffizient α in 10-6/K
Aluminium	23,8
Asphalt	ca. 200
Blei	29
Bronze	17,6
Chrom	6,6
Diamant	1,3
Eis (0°C)	0,502
Eisen	12,1
Gold	14,3
Graphit	7,9
Jod	83
Kalium	84
Kalk	ca.20
Kupfer	16,8
Magnesium	26
Mangan	23
Marmor	ca. 11
Messing	18
Natrium	71
Natriumchlorid	40
Nickel	12,8
Phenol	290
Platin	9
Polyamid	100 ..140
Polystyrol	60 .. 80
Porzellan	3 .. 4
Silber	19,7
Stahl	10 .. 16
Titan	9
Wolfram	4,3
Zink	27
Zinn	27

  
 

 
In der nachfolgend angeordneten Tabelle sind die Volumenausdehnungskoeffizienten (bei 20°C) einiger Flüssigkeiten aufgeführt.
 

Flüssigkeit	Volumenausdehnungs-koeffizient γ in 10-6/K
Benzin	106
Benzol	124
Brom	112
Chloroform	128
Ethanol	110
Glycerin	50
Heptan	124
Hexan	135
Methanol	120
Oktan	114
Pentan	160
Petroleum	96
Quecksilber	18,1
Salpetersäure	124
Schwefelsäure	57
Wasser	20,7
Xylol	98

 
 

 
In der nachfolgend angeordneten Tabelle sind die Volumenausdehnungskoeffizienten (bei 103,3 kPa und 0..100°C) einiger Gase aufgeführt.
 

Gas	Volumenausdehnungs-koeffizient γ in 10-6/K
Ammoniak	377
Argon	368
Chlor	383
Ethan	375
Helium	366
Kohlendioxid	373
Kohlenmonoxid	367
Luft	367
Methan	368
Neon	366
Sauerstoff	367
Schwefeldioxid	385
Stickstoff	367
Wasserdampf	394
Wasserstoff	366

  
  

 
In der nachfolgend angeordneten Tabelle sind die Wärmeleitfähigkeiten (thermische Leitfähigkeiten) (bei 20°C) einiger Stoffe aufgeführt.
 

Stoff	Wärmeleitfähigkeit λ in W/(m·K)
Aluminium	220
Argon	0,0173
Basalt	1,6
Benzin	0,12
Benzol	0,148
Beton	ca. 1
Blei	34,8
Eis	2,2
Eisen	74
Ethanol	0,165
Gold	312
Graphit	169
Gummi	0,15
Helium	0,15
Holz	0,1.. 0,2
Kohendioxid	0,016
Kupfer	384
Luft	0,026
Magnesium	171
Methanol	0,198
Milch	0,55
Natrium	126
Nickel	91
Petroleum	0,127
Platin	70
Polyamid	0,26
Polyethylen	0,4
Polystyrol	0,15
Porzellan	1
Propan	0,017
Quecksilber	8,2
Sauerstoff	0,026
Schaumstoff	0,04
Silber	407
Stahl	45
Stickstoff	0,026
Styropor	0,036
Titan	22
Wasser	0,598
Wasserstoff	0,184
Wolfram	177
Zink	112
Zinn	65

 
 

 
Nachfolgende Tabelle (Heizwerttabelle) zeigt die Heizwerte einiger fester Brennstoffe (bei 20° C).
 

Fester Brennstoff	Heizwert Hu in [MJ/kg]
Braunkohlebriketts	19 - 21,5
Graphit	28 - 35
Holz (waldfrisch)	6,8
Holz (lufttrocken)	14,4 - 15,8
Holzbriketts	18 - 18,6
Holzkohle	28 - 35
Koks	28 - 35
Magnesium	25
Phosphor	25
Steinkohle	25 - 32
Torf (trocken)	14

 
 

 
Nachfolgende Tabelle (Heizwerttabelle) zeigt die Heizwerte einiger flüssiger Brennstoffe (bei 20° C).
 

Flüssiger Brennstoff	Heizwert Hu in [MJ/kg]
Benzin	40,1 - 41,8
Benzol	40,1
Diesel	42,6
Erdöl	42,8
Heizöl (schwer)	42,6
Heptan	44
Hexan	44,6
Methanol	19,8
Oktan	44,5
Petroleum	40,7

 
 

 
Nachfolgende Tabelle (Heizwerttabelle) zeigt die Heizwerte einiger gasförmiger Brennstoffe (Gase) (bei 20° C und 101325 Pa).
 

Gasförmiger Brennstoff	Heizwert Hu in [MJ/m³]
Acetylen	56,49
Ammoniak	14,2
Ethan	64,34
Ethylen	59,45
Erdgas	31 - 41
Gichtgas	2,5 - 3,3
Kohlenmonoxid	12,6
Methan	35,8
Propan	93,21
Stadtgas	17 - 18
Wasserstoff	10,8

 

Tabelle - Emissionsgrad

 
Nachfolgend gezeigte Tabelle gibt Auskunft über den Emissionsgrad ε einiger Stoffe.
 

Werkstoff	Oberfläche	t [°C]	ε
Aluminium	poliert	20	0,04
	gewalzt	20	0,07
	sandgegossen	20	0,3
Beton		20	0,87
Blei	oxidiert	20	0,29
Chrom	poliert	150	0,076
Eisen	blank	20	0,29
	gerostet	20	0,65
Eis	glatt	0	0,92
Gips		20	0,8 - 0,9
Gold	poliert	20	0,02
Glas		90	0,08
Gußeisen	blank	20	0,25
	poliert	20	0,6 - 0,8
Kupfer	blank	20	0,04
	angelaufen	20	0,05
	oxidiert (schwarz)	20	0,6 - 0,8
Holz		20	0,85 - 0,95
Messing	poliert	20	0,05
Nickel	poliert	100	0,055
Kunststoffe		20	0,9
Platin	poliert	100	0,05
Papier		20	0,9
Porzellan	glasiert	20	0,95
Quecksilber		0 .. 100	0,09 - 0,12
Sand			0,76
Schwarzer Körper			1
Silber		20	0,02
Stahlblech	gewalzt	20	0,67
	poliert	20	0,285
	verrostet	20	0,85
Wasser		0 - 100	0,92
Wolfram		100	0,03
Zink	oxidiert	20	0,25
Zinn	poliert	20	0,06

     

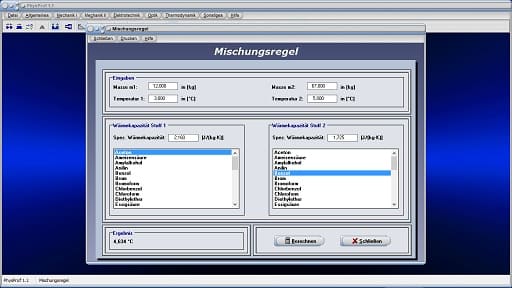
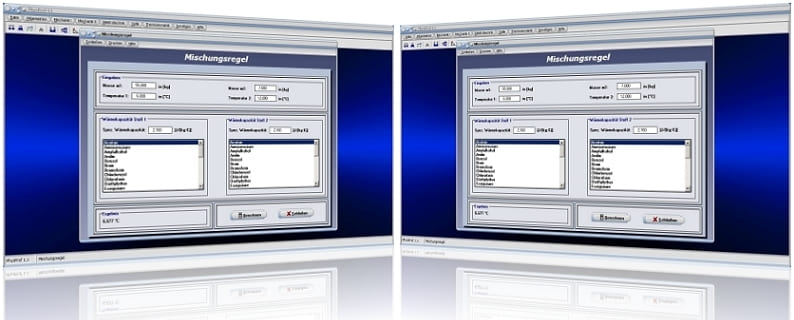
Mischungsregel - Abbildung 3


Mischungsregel - Abbildung 4

 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

 
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 
  

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.

 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Richmannsche Mischungsregel zu finden.
 

 

Isochore Zustandsänderung - Isobare Zustandsänderung - Isotherme Zustandsänderung - Adiabatische Zustandsänderung - Carnotscher Kreisprozess - Aggregatzustände - Reales Gas - Molekülgeschwindigkeit
 

    

Unterprogramm Mischungsregel
 

 

PhysProf 1.1 - Unterprogramm RLC-Kreis
 

MathProf 5.0 - Unterprogramm Kurven in Parameterform
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

 

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

 
 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---