MathProf - Geradensteigung - Steigung - Steigungsdreieck - Anstieg - Gefälle

Fachthema: Geradensteigung - Steigung einer Geraden
MathProf - Geometrie - Software für interaktive Mathematik und zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen. Ein Programm zum Einsatz im Mathematikunterricht sowie für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung interaktiver grafischer Untersuchungen, um sich das Prinzip der Ermittlung einer Geradengleichung in Steigungsform verständlich zu machen.
In diesem Teil des Programms wird es bei Ausgabe der entsprechenden Grafik unter anderem ermöglicht, die Steigung (den Steigungsfaktor) sowie den y-Achsenabschnitt einer Gerade dieser Form festzulegen und den Steigungswinkel einer Geraden dieser Art berechnen zu lassen.
Auch das entsprechende Steigungsdreieck der definierten linearen Funktion wird dargestellt. Verläuft diese Gerade durch den Koordinatenursprung, so spricht man von einer proportionalen Funktion.
Das Berechnen der Werte erforderlicher Größen erfolgt zur Echtzeit. Der Rechner stellt die entsprechenden Zusammenhänge unmittelbar nach Eintritt einer interaktiven Operation dar. Jedes relevante Ergebnis einer durchgeführten Berechnung zu diesem Fachthema wird aktualisiert ausgegeben.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Steigung einer Gerade - Geradensteigung - m - Gerade - Geradengleichung - Steigung - Steigungsform - Vektoren - Anstieg - Steigungswinkel - Definitionsgleichung - Steigungsdreieck - Abschnitt - Achsenabschnitt - Achse - Ordinatenwert - Steigungsdreieck zeichnen - Steigung bestimmen - Steigungswinkel bestimmen - Herleitung - Beweis - Verhältnis - Anstieg in Prozent - Anstieg um - Gefälle - Neigung - Prozent - Prozentual - Prozentualer Anstieg - Prozentualer Zuwachs - Prozentuale Steigung - Prozentuales Gefälle - Prozentuale Zunahme - Prozentuale Abnahme - Prozentuales Verhältnis - Prozentuales Wachstum - Steigung in Grad - Gefälle berechnen - Grad - Grad in Prozent - Prozent in Grad - Neigungswinkel - Anstiegswinkel - Anstiegsdreieck - Verschiebung einer Gerade - Y-Achsenabschntt - Fallend - Steigend - Winkel - Positiv - Negativ - Tangens - Bild - Grafik - Ermitteln - Formel - Graph - Plotter - Bilder - Berechnen - Rechner - Bestimmen - Einführung - Ermittlung - Erklärung - Einfach erklärt - Welche - Welcher - Welches - Wodurch - Beschreibung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Definition - Begriff - Begriffe - Zeichnen - Darstellung - Berechnung - Darstellen - Grafische Darstellung - Lineare Funktion - Höhenunterschied berechnen - Hang - Hangneigung - Abszissenabschnitt - Ordinatenabschnitt - Höhendifferenz |
Geradensteigung
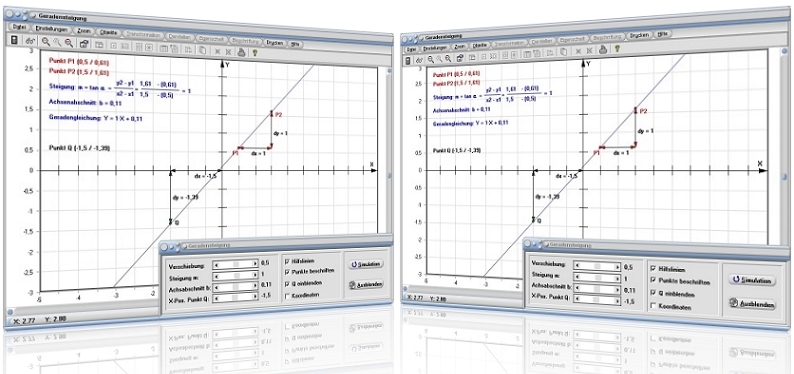
Modul Geradensteigung
Das kleine Unterprogramm [Geometrie] - [Gerade] - Geradensteigung stellt eine Methode zur Verfügung, um sich das Prinzip der Ermittlung einer Geradengleichung in Steigungsform verständlich zu machen.

Die Steigung (der Anstieg) einer Geraden (linearen Funktion) gibt Auskunft darüber, um wie viele Einheiten sich die y-Koordinate eines Punktes auf der Geraden verändert, wenn sich seine x-Koordinate um exakt eine Einheit verändert. Sie wird als Geradensteigung bezeichnet und ist ein Maß für ihre Steilheit. Die Steigung einer Geraden, welche parallel zur x-Achse verläuft, beträgt 0. Die Steigung einer Geraden, welche parallel zur y-Achse verläuft, ist "unendlich".
Ein Steigungsdreieck kann an jedem beliebigen Punkt einer Geraden angesetzt werden. Dieses wird von einem auf der Geraden liegenden Punkt P1 ausgehend mit dem Faktor m = Δy / Δx bzw. dy/dx gezeichnet.
Die Definitionsgleichung einer Geradengleichung (linearen Funktion) in Steigungsform lautet:
y = m·x+b
m: Steigung (Anstieg) der Geraden
b: Achsenabschnitt der Geraden
Die Steigung m der Geraden wird aus zwei, auf ihr liegenden, Punkten P1 (x1;y1) und P2 (x2;y2) wie folgt ermittelt:

Der zugehörige y-Achsenabschnitt b (Ordinatenabschnitt) besitzt den Ordinatenwert des Schnittpunkts der Geraden mit der y-Achse.
Als Steigungswinkel (Neigungswinkel) einer Geraden wird derjenige im mathematisch positiven Sinne gemessene Winkel α bezeichnet, den die Gerade mit dem positiven Bereich der Abszisse (x-Achse ) einschließt.
Ein Steigungsdreieck gibt die Steigung m einer Geraden an. Es erteilt Auskunft darüber, wie stark eine Funktion ansteigt bzw. fällt.
Als Achsenabschnitt (Abschnitt) wird der Abstand bezeichnet, der zwischen dem Schnittpunkt der Gerade mit einer der Koordinatenachsen und dem Koordinatenursprung vorliegt.
Prozentualer Anstieg (prozentualer Zuwachs oder prozentuale Zunahme) - Prozentuales Gefälle - Prozentuale Abnahme - Prozentuales Wachstum:
Der prozentuale Anstieg (der prozentuale Zuwachs, die prozentuale Zunahme, die prozentuale Steigung, der Anstieg in Prozent bzw. die Geradensteigung) wird errechnet, indem der Anfangswert und Endwert durch den Anfangswert geteilt wird und dieses Ergebnis mit der Zahl 100 multipliziert wird. Bei einem prozentualen Gefälle (einer prozentualen Abnahme) geschieht dies in gleicher Form unter Berücksichtigung, dass in diesem Fall der Anfangswert größer dem Endwert zu sein hat.
Steigung in Prozent: Eine Steigung in Prozent kann berechnet werden, indem die Höhe durch die horizontale Strecke geteilt wird und dieses Ergebnis mit der Zahl 100 multipliziert wird.
Gefälle: Als Gefälle wird eine Steigung mit einem negativen Wert bezeichnet.
Höhenunterschied (Höhendifferenz): Als Höhenunterschied (Höhendifferenz) wird der Unterschied in der Höhenlage zwischen zwei verschiedenen Punkten bezeichnet.
Prozentuales Verhältnis: Ein prozentuales Verhältnis wird berechnet, indem der Prozentwert durch den Grundwert geteilt wird und das Ergebnis hierauf mit der Zahl 100 multipliziert wird.
Steigung (Geradensteigung) in Grad umrechnen: Um aus einer Prozentangabe eine Steigung in Grad zu ermitten, wird der arcustangens des durch 100 geteilten Prozentwerts berechnet.
Eine Steigung (Geradensteigung) von Grad in Prozent umrechnen: Gradangaben können wie nachfolgend gezeigt in Prozentangaben umgerechnet werden: Steigung in Prozent = 100·tan(α), mit α in Grad.
Eine Steigung (Geradensteigung) von Prozent in Grad umrechnen: Prozentangaben können wie nachfolgend gezeigt in Grad umgerechnet werden: α = 360·p/100, mit p in Prozent.
Der Neigungswinkel zwischen einer Hangfläche und der Horizontalen wird als Hangneigung bezeichnet.
Als Abszissenabschnitt ist der Abszissenwert definiert bei dem der Graph einer Funktion die x-Achse schneidet.
Als Ordinatenabschnitt ist der Ordinatenwert definiert bei dem der Graph einer Funktion die y-Achse schneidet.
Anstieg - Gefälle - Neigung - Prozentualer Anstieg - Prozentuales Gefälle
Anstieg: Unter dem Begriff Anstieg wird in der Mathematik die Steigung einer Geraden (bzw. eines Funktionsgraphen) in einem kartesischen Koordinatensystem verstanden.
Neigung: Eine Neigung beschreibt in der Mathematik den Verlauf einer Geraden bezüglich der horizontalen Achse oder der Lotachse.
Nachfolgend wird auf die Berechnung eines Anstiegs bzw. eines Gefälles eingegangen. Diese Werte lassen sich durch die im Folgenden gezeigte Vorgehensweise ermitteln.
1. Berechnung einer Steigung (eines prozentualen Anstiegs):
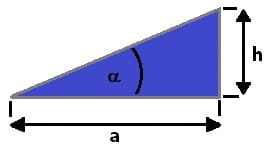
Beispiel:
Gegeben seien eine waagerecht verlaufende Strecke a mit der Länge 10 m sowie eine unter rechtem Winkel positionierte, vertikale Höhe (Höhendifferenz) h = 4 m (siehe vorige Abbildung). Es ist der Wert für den prozentualen Anstieg dieser Anordnung zu ermitteln.
Gegeben sind somit:
a = 10 m
h = 4 m
Der Neigungswinkel (bzw. der Anstiegswinkel) kann durch die Nutzung der trigonometrischen Winkelfunktion Tangens sowie derer Umkehrfunktion Arcustangens berechnet werden. Hierbei gilt:
tan α = h/a
Somit beträgt der in diesem Fall vorliegende Neigungswinkel (im Bogenmaß):
α = arctan(h/a) = arctan(4/10) = arctan(0,4) = 0,3805
Ergebnisse:
Die Steigung besitzt demzufolge den Wert 0,3805.
Im Gradmaß beträgt der Steigungswinkel α = 0,3805·180/Pi = 21,8°
Dies entspricht einem prozentualen Anstieg (einer prozentualen Zunahme bzw. einem prozentualen Wachstum) von 40%, da das Verhältnis a/h = 4/10 = 0.4 beträgt.
2. Berechnung eines Gefälles (einer prozentualen Neigung):
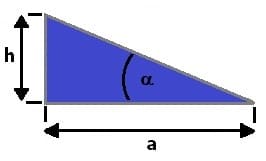
Beispiel:
Gegeben seien eine waagerecht verlaufende Strecke a mit der Länge 12 m sowie eine unter rechtem Winkel positionierte, vertikale Höhe (Höhendifferenz) h = 3 m (siehe vorige Abbildung). Es ist der Wert für das prozentuale Gefälle dieser Anordnung zu ermitteln.
Gegeben sind somit:
a = 12 m
h = 3 m
Der Neigungswinkel (bzw. der Anstiegswinkel) kann durch die Nutzung der trigonometrischen Winkelfunktion Tangens sowie derer Umkehrfunktion Arcustangens berechnet werden. Hierbei gilt:
tan α = h/a
Somit beträgt der in diesem Fall vorliegende Neigungswinkel (im Bogenmaß):
α = arctan(h/a) = arctan(3/12) = arctan(0,25) = 0,245
Ergebnisse:
Das Gefälle (die Hangneigung) besitzt demzufolge den Wert 0,245.
Im Gradmaß beträgt der Steigungswinkel α = 0,245·180/Pi = 14,036°
Dies entspricht einem prozentualen Gefälle (einer prozentualen Abnahme) von 25%, da das Verhältnis (das prozentuale Verhältnis) 3/12 = 0,25 beträgt.
Darstellung
In diesem Modul können durch die Positionierung der entsprechenden Schieberegler die Werte für die Steigung m, wie auch für den Achsenabschnitt b einer Geraden eingestellt werden. Außerdem kann durch die Positionierung des Schiebereglers Verschiebung ein Steigungsdreieck entlang des Geradenverlaufs bewegt werden.
Wird Kontrollschalter Q einblenden aktiviert, so kann durch die Bedienung des Schiebereglers X-Pos. Punkt Q, ein auf der Geraden liegender Punkt Q, entlang des Geradenverlaufs verschoben werden und dessen horizontaler, wie vertikaler Abstand zum Koordinatenursprung abgelesen werden. Der Abszissenwert des Punkts Q wird hierbei durch die Position dieses Schiebereglers bestimmt.
Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. den Wert für die zu verwendende Verzögerung einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformular

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
- Hilfslinien: Darstellung von Hilfslinien ein-/ausschalten
- Punkte beschriften: Beschriftung der Punkte des Steigungsdreiecks und des Punktes Q ein-/ausschalten
- Q einblenden: Darstellung eines auf der Gerade positionierbaren Punktes Q, sowie die Ermittlung der Abstände dessen zu den Koordinatenachsen, ein-/ausschalten
- Koordinaten: Koordinatenwertanzeige markanter Punkte ein-/ausschalten
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Achsenabschnittsform einer Geraden
Punkt-Richtungs-Form einer Geraden
Zwei-Punkte-Form einer Geraden
Hessesche Normalenform einer Geraden
Beispiel
Wurde der Schieberegler Steigung m auf den Wert -1,5 und der Schieberegler Achsenabschnitt b auf den Wert 3 eingestellt, so wird die Gerade mit der Gleichung Y = -1,5·X+3 dargestellt. Wird hierauf die Position des Rollbalkens Verschiebung verändert, so kann u.a. festgestellt werden, dass der Wert der ermittelten Geradensteigung stets konstant bleibt.
Wird die Steigung der Geraden in den Punkten P1 (0,5 / 2,3) und P2 (1,5 / 0,8) ermittelt, so besitzt sie den Wert:

Wird sie hierauf beispielsweise in den Punkten P1 (2,1 / -0,2) und P2 (3,1 / -1,7) ermittelt, so besitzt sie ebenfalls den Wert:

Da der Achsenabschnitt der Geraden mit b = 3 festgelegt wurde, kann die Gleichung der Geraden beschrieben werden mit: Y = -1,5·X+3

Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2

Grafische Darstellung - Beispiel 3

Grafische Darstellung - Beispiel 4
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Punkt-Steigungsform zu finden.


Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
MathProf 5.0 - Unterprogramm Gerade - Punkt

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.















