MathProf - Logische Aussagen - Boolesche Operatoren - Logik

Fachthemen: Aussagenlogik und Boolesche Algebra
MathProf - Mathematische Logik - Software für interaktive Mathematik zum Lösen unterschiedlicher Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung von Operationen mit logischen Aussagefunktionen.
Dieser Teil des Programms ermöglicht die Erstellung logischer Verknüpfungen sowie deren Auswertung unter der Verwendung frei definierbarer Funktionen mit bis zu fünf verschiedenen Variablen sowie mit Hilfe relevanter logischer Operatoren.
Hierbei handelt es sich um ein Unterprogramm zur Anwendung der Booleschen Algebra aus dem Bereich der Digitaltechnik, bei welchem unter anderem die folgenden logischen Funktionen zur Definition kombinierter Aussagen verwendet werden können: UND (Konjunktion), ODER (Disjunktion), XOR, NOR, NAND sowie Implikation, Negation und Äquivalenz.
Die Ausgabe der Ergebnisse definierter Fallunterscheidungen erfolgt in einer Wahrheitstabelle (Funktionstabelle) bzw. Wahrheitstafel. Auch ermöglicht der implementierte Rechner die Bildung derer disjunktiver und konjunktiver Normalform.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind eingebunden.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Aussagenlogik - Aussagen - Logik - Tabelle - Wahrheitstafel - Wahrheitstabelle - Logische Verknüpfungen - Logische Operatoren - Zeichen - Logische Aussagen - Aussagenlogische Formel - Gleichungen - 0 - 1 - A - B - Verknüpfungen - Verknüpfungstafel - Funktionstabelle - Wahrheitstafeln - Wahrheitstabellen - Kontravalenz - Äquivalenz - Was sind - Was ist - Bedeutung - Was bedeutet - Welche - Welcher - Welches - Wodurch - Herleitung - Beweis - Einführung - Erklärung - Einfach erklärt - Beschreibung - Disjunktive Normalform - Konjunktive Normalform - Disjunktion - Konjunktion - Konklusion - Wenn - Dann - Operationen - Anweisungen - Bedingungen - Mehrere Bedingungen - Boolesche Logik - Boolesche Operatoren - Boolesche Algebra - Argumente - Ausdrücke - Aussageform - Ausdruck - Ergebnis - Übersicht - Logische Funktionen - Logisches Oder - Logisches Und - Verschachtelte Wenn Funktion - Wahr - Falsch - Gesetze - Entweder oder - Operator - Mathematische Aussagen - Mathe - Rechnen - Implikationen - Kontraposition - Berechnung - Wenn Funktionen - Wenn Oder Funktion - OR - NOR - NAND - XOR - UND - ODER - AND - Implikation - NAND-Verknüpfung - NOR-Verknüpfung - Und-Verknüpfung - Oder-Verknüpfung - OR-Verknüpfung - XOR-Verknüpfung - XOR-Tabelle - NAND-Tabelle - Oder-Funktion - Und-Funktion - XOR-Funktion - NOR-Funktion - NOR-Tabelle - NAND-Funktion - NAND-Tabelle - NOR-Operator - NAND-Operator - Regeln - Klammern - Grundlagen - Lösen - Definition - Unterschied - Existenzquantor - Kommutativgesetz - Rechengesetze - Assoziativgesetz - Distributivgesetz - Informatik - Methode - Operation - Operator - Und - Oder - Nicht oder - Nicht und - Tautologie - Kontradiktion - Beziehungen - Logische Ausdrücke - Richtig - Verknüpfen - Junktoren - Umkehrung - Umkehren - Negation - Schaltungen - Mathematik - Negieren - Verneinung - Gesetze - De Morgan-Regeln - Logisch - Grundlagen - Grundlegendes - Übersicht - Begriff - Begriffe - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Zeichen - Negation - Negierung - Beispiel - Wertetabelle - Rechner - Berechnen - Formel - Formeln - Funktion - Funktionen - Logische Negation - Ergebnis - Schaltfunktionen - Idempotenz - Darstellen - Darstellung - Aufgaben - Lösungen - Logikgatter - Gatter - Boolesche Funktion - Rechenregeln - De Morgan - De Morgansche Regeln - De Morgansche Gesetze - De Morgansches Theorem |
Aussagenlogik - Boolesche Algebra
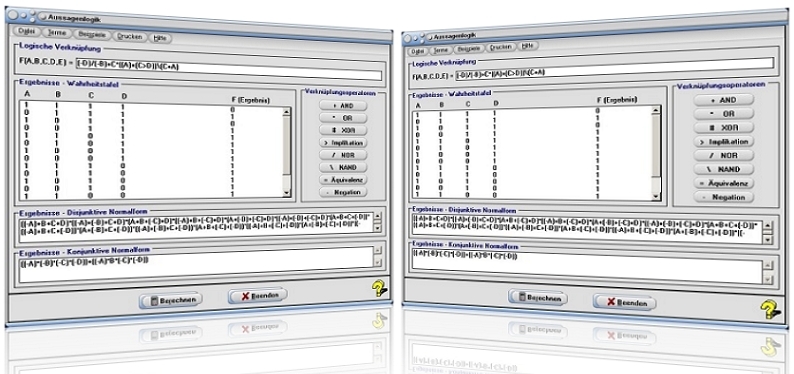
Modul Aussagenlogik
Unter dem Menüpunkt [Sonstiges] - Aussagenlogik können Operationen mit in der Booleschen Algebra definierten Aussagefunktionen in Tabellenform (Wahrheitstabelle) ausgegeben und ausgewertet werden.

Die Boolesche Algebra stellt eine mathematische Struktur dar, die auf der Grundlage binärer logischer Operationen basiert und die lediglich die Zahlen 0 und 1 benutzt.
Eine mathematische Aussage ist entweder wahr, oder falsch. Sie kann nur eine dieser Eigenschaften besitzen. Ausgedrückt wird dies durch die Benutzung der boolschen Wahrheitswerte Wahr (1) oder Falsch (0).
Durch die Verwendung von Operatoren und Operationen mit Aussagen, die als Aussagefunktionen bezeichnet werden, können kombinierte Aussagen daraufhin überprüft werden, ob sie wahr oder falsch sind.
Verknüpfte Aussagen werden u.a. in den Bereichen der Begründung mathematischer Beweistechniken, der Mengentheorie, sowie in der Schaltalgebra (Digitaltechnik) benötigt.
Die Aussagenlogik oder Boolesche Logik ist ein Teilgebiet der formalen Logik, die die zwischen Aussagen und Aussagenverbindungen bestehenden Beziehungen untersucht. Sie beschäftigt sich mit Aussagen und deren Verknüpfung durch Junktoren. Jeder Aussage wird hierbei ein Element der Booleschen Algebra als Wahrheitswert zugeordnet.
Zusammenhänge - Operatoren - Aussagefunktionen - Symbole - Übersicht
Zur Definition von Aussagefunktionen (elementaren Aussagen) stehen die folgenden 8 Funktionen und Operatoren (Zeichen) zur Verfügung:
| Aussagefunktion | Operator | |
| AND (Konjunktion, Und) | + | Wahr, wenn beide Aussagen zugleich wahr sind |
| OR (Disjunktion, Oder) | * | Wahr, wenn eine der beiden Aussagen wahr ist |
| XOR (Entweder oder) | # | Wahr, wenn entweder die eine oder die andere Aussage wahr ist |
| Implikation (Wenn ... so) | > | Nur falsch, wenn aus einer wahren Aussage eine falsche geschlussfolgert werden soll |
| NOR | / | Falsch, wenn beide Aussagen wahr sind |
| NAND | \ | Wahr, wenn beide Aussagen falsch sind |
| Äquivalenz (Genau dann, wenn) | = | Wahr, wenn beide Aussagen den gleichen Wahrheitswert besitzen |
| Negation (NOT, Nicht) | - | Wahr, wenn Ausgangsaussage falsch ist |
Nachfolgend wird die Tabelle der Wahrheitswerte gezeigt, die sich bei Verwendung der Aussagen A und B ergeben. Es sind hierbei genau 4 Kombinationen von Aussagen und Operationen möglich.
| A | B | A+B | A*B | A#B | A>B | A=B | A/B | A\B | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
Regeln der Aussagenlogik - Regeln der Aussagenverknüpfung - Logische Verknüpfungen - Grundlagen
Wenn eine Aussageform für alle Elemente einer Grundmenge erfüllt ist, so heißt sie allgemeingültig. Zwischen Aussagen beziehungsweise derer Verknüpfungen sind nachfolgend aufgeführte Äquivalenzen definiert, welche durch die entsprechenden Junktoren (Symbolzeichen) miteinander in Verbindung stehen:
Kommutativgesetz:
A1 ∧ A2 ⇔ A2 ∧ A1
A1 ∨ A2 ⇔ A2 ∨ A1
Assoziativgesetz:
( A1 ∧ A2 ) ∧ A3 ⇔ A1 ∧ ( A2 ∧ A3 )
( A1 ∨ A2 ) ∨ A3 ⇔ A1 ∨ ( A2 ∨ A3 )
Distributivgesetz:
A1 ∧ ( A2 ∨ A3 ) ⇔ ( A1 ∧ A2 ) ∨ ( A2 ∧ A3 )
A1 ∨ ( A2 ∧ A3 ) ⇔ ( A1 ∨ A2 ) ∧ ( A2 ∨ A3 )
De Morgan-Regeln:
¬( A1 ∧ A2 ) ⇔ ( ¬A1 ) ∨ ( ¬A2 )
¬( A1 ∨ A2 ) ⇔ ( ¬A1 ) ∧ ( ¬A2 )
Absorptionsgesetz:
A1 ∧ ( A1 ∨ A2 ) ⇔ A1
A1 ∨ ( A1 ∧ A2 ) ⇔ A1
Idempotenzgesetz:
A ∧ A ⇔ A
A ∨ A ⇔ A
Komplementgesetz:
A1 ∨ ( ¬A2 ∧ A2 ) ⇔ A
A1 ∧ ( ¬A2 ∨ A2 ) ⇔ A
Mit:
A, A, A2: Aussagen
Junktoren:
∧: Logisches Und
∨: Logisches Oder
¬: Nicht
⊻: Entweder ... oder
Fachbegriffe
Im folgenden sind die Bedeutungen einiger Begriffe zu diesem Fachthema aufgeführt.
Logik: Als Logik wird die Lehre von den Prinzipien des richtigen, somit schlüssigen Denkens und Beweisführens bezeichnet.
Wahrheitstafeln (Wahrheitstabellen): Eine Wahrheitstafel (Wahrheitstabelle) ist eine tabellarische Aufstellung des Wahrheitswertverlaufs logischer Aussagen.
Logische Aussagen: Bei einer logischen Aussage handelt es sich um einen Satz oder Ausdruck, der entweder wahr (1) oder falsch (0) sein kann.
Logische Verknüpfungen: Als logische Verknüpfung wird eine Operation der Booleschen Algebra bezeichnet. Durch Vernüpfungen dieser Art werden in der Schaltalgebra sowie der Aussagenlogik aus einfachen Aussagen kompliziertere Aussagen zusammengesetzt.
Boolesche Operatoren: Ein boolescher Operator stellt einen logischen Operator dar. Er ist somit ein Operator, der mit Wahrheitswerten operiert.
Fallunterscheidung: Eine Fallunterscheidung ist eine Unterscheidung, die dazu dient, alternative Abläufe zu beschreiben.
Logische Funktionen: Logische Funktionen werden verwendet, um zu prüfen, ob bestimmte Fakten bzw. Bedingungen gegeben sind, oder nicht. Hierzu zählen unter anderem die UND-Funktion, die ODER-Funktion, die NICHT-Funktion und die WENN-Funktion sowie weitere Aussagefunktionen.
Kontravalenz: Eine logische Kontravalenz bezeichnet die Verbindung zweier Aussagen durch die Teilaussagen entweder - oder. Es hat exakt eine der beiden Aussagen zutreffen, entweder die eine oder die andere. Keine der beiden Aussagen sind zugleich wahr oder falsch.
Äquivalenz: Eine logische Äquivalenz liegt gann vor, wenn zwei logische Ausdrücke ein und denselben Wahrheitswert besitzen.
Disjunktion: Mit dem Begriff Disjunktion wird das logische Oder beschrieben. Es ist genau dann wahr, wenn von zwei Aussagen wenigstens eine dieser wahr ist. Die Disjunktion in der Aussagenalgebra entspricht der Vereinigung in der Mengenalgebra und der Addition in der Booleschen Algebra.
Disjunktive Normalform (nicht ausschließendes ODER): Hiebei handelt es sich um einen logischen Ausdruck, der in der obersten Ebene aus ODER-Verknüpfungen besteht. Er besitzt folgendes Aussehen: A oder B oder C oder D. Einzelne Elemente dieser Verknüpfung können auch UND-Verknüpfungen beinhalten. Bespiel: (A und B) oder B (und A und C) oder C (und A) oder D
Konjunktion: Der Ausdruck Konjunktion beschreibt das logische Und. Dieses ist genau dann wahr, wenn von zwei Aussagen beide Teilaussagen wahr sind. Die Konjunktion in der Aussagenalgebra entspricht dem Durchschnitt in der Mengenalgebra und dem Produkt in der Booleschen Algebra.
Kontraposition: Als Kontraposition wird der Umkehrschluss einer Implikation verstanden. Für sie gilt somit der Schluss: Wenn A, dann B auf Wenn nicht B, dann nicht A.
Tautologie: Als Tautologie wird eine Aussage bezeichnet, die stets wahr ist, unabhängig vom Wahrheitswert der zugrundeliegenden Bestandteile.
Kontradiktion: Um eine Kontradiktion handelt es sich, wenn zwei Aussagen oder Begriffe im gegenseitigen Widerspruch stehen und sie eine gegenseitige Negation darstellen.
Konklusion: In der Logik wird eine Konklusion als Aussage definiert, die durch ein logisches Schlussfolgern aus einer oder mehrerer Prämissen gewonnen wird.
Logikgatter: Logikgatter sind Anordnungen (elektronische Schaltungen), die Wahrheitswerte verarbeiten und zur Umsetzung einer booleschen Funktion, binäre Eingangssignale zu einem binären Ausgangssignal verarbeiten. Es wird zwischen drei Grundtypen von Logikgattern unterschieden: Dies sind das UND-Gatter, das ODER-Gatter sowie das NICHT-Gatter.
Existenzquantor: Ein Existenzquantor ist ein Operator, der zum Ausdruck bringt, dass es mindestens ein Objekt gibt, welches bestimmte Bedingungen erfüllt.
Junktoren: Als Junktoren werden Zeichen oder Worte bezeichnet, die Teilaussagen in einer Form zu einer Gesamtaussage verknüpfen, dass der Wahrheitswert der resultierenden Gesamtaussage einzig und allein von den Wahrheitswerten dieser Teilaussagen bestimmt wird.
Aussageform: Unter einer Aussageform handelt es sich in der Logik um Ausdrücke deren Wahrheit oder Falschheit noch nicht bekannt ist.
Mathematische Aussage: Eine mathematische Aussage ist eine Behauptung, bei der feststeht, dass sie falsch oder wahr ist.
Implikationen: Eine Implikation ist eine Schlussfolgerung, die nur dann das Ergebnis falsch liefert, wenn aus einer wahren Aussage eine falsche geschlussfolgert werden soll.
Negation: Eine Negation ist eine Verneinung. Sie verneint eine Aussage.
Verknüpfungstafel: Eine Verknüpfungstafel ist eine quadratische Wertetabelle, in welcher alle möglichen Werte für eine Verknüpfung auf einer endlichen Menge angegeben werden.
Beispiele: Auf der Menge A = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 } werden die beiden folgenden Verknüpfungen betrachtet:
1. Die Addition a + b mod 5
2. Die Multiplikation a ⋅ b mod 5
Die beiden zuvor aufgeführten Verknüpfungen entsprechen den folgenden beiden Verknüpfungstafeln:
+ 0 1 2 3 4
0 0 1 2 3 4
1 1 2 3 4 0
2 2 3 4 0 1
3 3 4 0 1 2
4 4 0 1 2 3
⋅ 0 1 2 3 4
0 0 0 0 0 0
1 0 1 2 3 4
2 0 2 4 1 3
3 0 3 1 4 2
4 0 4 3 2 1
De Morgansche Gesetze - Funktionale Vollständigkeit
1. De Morgansche Gesetze:
Die De-Morganschen Gesetze (oft auch De-Morgansche Regeln genannt) sind zwei grundlegende Regeln für logische Aussagen. Bei ihnen handelt es sich um einen logischen Ausdruck, der aus ODER-Verknüpfungen besteht.
Die De-Morganschen Gesetze lauten in der Logik:
Nicht (a und b) ist äquivalent zu ((nicht a) oder (nicht b))
Nicht (a oder b) ist äquivalent zu ((nicht a) und (nicht b))
bzw.:
¬a(a∧b) ⇔ ¬a ∨ ¬b
¬a(a∨b) ⇔ ¬a ∧ ¬b
2. Funktionale Vollständigkeit:
Eine funktionale Vollständigkeit einer Menge von Grundverknüpfungen liegt vor, wenn alle Ausgangsverknüpfungen mit den Elementen einer Menge darstellbar sind. Es sind dies:
- Negation und Konjunktion
- Negation und Alternative
- Negation und Implkiation
- Anti-Alternative
- Anti-Konjugation
Wahrheitstabellen - Wahrheitstafel - Wahrheitswertetabelle - Logikgatter
Nachfolgend aufgeführt sind die Wahrheitstabellen (bzw. Logikgatter, Wahrheitstafeln, Wahrheitswertetabellen) wesentlicher logischer Aussagefunktionen.
1. Und-Verknüpfung
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. Oder-Verknüpfung
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
3. XOR-Verknüpfung
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
4. NOR-Verknüpfung
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
5. NAND-Verknüpfung
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Berechnung
Dieses Programmmodul ermöglicht die Erstellung von Aussagefunktionen und die Durchführung relevanter Rechenoperationen mit diesen.
Mit Hilfe der 8 zur Verfügung stehenden Funktionen können Sie in diesem Programmteil bis zu 5 Aussagen kombinieren. Eine kombinierte Aussage ist eine Funktion der Ausgangsaussagen H = F(A,B,C,D,E).
Nach der Definition einer Aussagefunktion im dafür vorgesehenen Eingabefeld und einer Bedienung der Schaltfläche Berechnen werden alle möglichen Belegungen der verwendeten Aussagen mit 0 (falsch), oder 1 (wahr) tabellarisch aufgelistet und die entsprechenden Wahrheitswerte im Tabellenfeld F (Ergebnis) der Wahrheitstabelle ausgegeben. Außerdem ermittelt das Programm die konjunktive und die disjunktive Normalform des logischen Terms und gibt diese aus.
Kann eine Aussagefunktion aufgrund eines Definitionsfehlers nicht ausgewertet werden, so erhalten Sie eine entsprechende Fehlermeldung.
Beachten Sie:
Bei der Definition einer Negation ist der Ausdruck in Klammern zu setzen. Der Ausdruck A+-B beispielsweise kann nicht ausgewertet werden. Er müsste wie folgt deklariert sein: A+(-B)
Um definierte Terme zu speichern, oder bereits gespeicherte Terme zu holen, verwenden Sie den Menüeintrag Terme - Terme speichern bzw. Terme - Terme holen.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung oder einem mathematischen Beweis zu folgen.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Beispiele
Beispiel 1:
Die Aussagen A und B sollen UND-verknüpft werden. Nach der Definition der Verknüpfungen im Eingabefeld mit der Zeichenfolge A+B werden nach einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse ausgegeben.
| A | B | F |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 0 |
Hieraus ist zu entnehmen:
Die Aussagenoperation A+B liefert nur das Ergebnis wahr, wenn die beiden Aussagen A und B zugleich wahr sind.
Für die disjunktive Normalform gibt das Programm den Term (A+B) aus. Die konjunktive Normalform des Ausdrucks lautet: (A* (B))+((-A)*B)+(A*B)
Beispiel 2:
Nach der Definition der aussagenlogischen Verbindung A*(B+C)=A im Eingabefeld und einer Bedienung der Schaltfläche Berechnen wird folgende Wahrheitswertetabelle ausgegeben:
| A | B | C | F |
| 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 |
Hieraus ist zu entnehmen:
Die Aussagenoperation A*(B+C)=A liefert nur das Ergebnis falsch, wenn Aussage A falsch ist, B und C zugleich wahr sind.
Für die disjunktive Normalform gibt das Programm den Term (A+B+C)*(A+(-B)+C)*((-A)+(-B)+C)*(A+B+(-C))*((-A)+B+(-C))*(A+(-B)+(-C))*((-A)+(-B)+(-C)) aus. Die konjunktive Normalform des Ausdrucks lautet: (A*(-B)*(-C))

Beispiel 1

Beispiel 2

Beispiel 3

Beispiel 4

Beispiel 5

Beispiel 6
Dieses Modul eignet sich neben vielem anderem auch zum Üben bereits erlernter Kenntnisse zu diesem Fachthema. Übungsaufgaben lassen sich durch benutzerdefinierte Festlegungen und Eingaben erstellen und unmittelbar hierauf numerisch bzw. grafisch auswerten. Übungen zu diesem Themengebiet können somit auf einfache Weise praktiziert werden, oder dazu genutzt werden, die Lösungen gestellter Aufgaben zu überprüfen und zu analysieren.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Aussagenlogik sowie unter Wikipedia - Wahrheitstabelle und unter Wikipedia - Logische Verknüpfung zu finden.
Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach
MathProf 5.0 - Unterprogramm Zahlentypumwandlung

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















