MathProf - Gebrochenrationale Funktion - Asymptoten - Pole

 

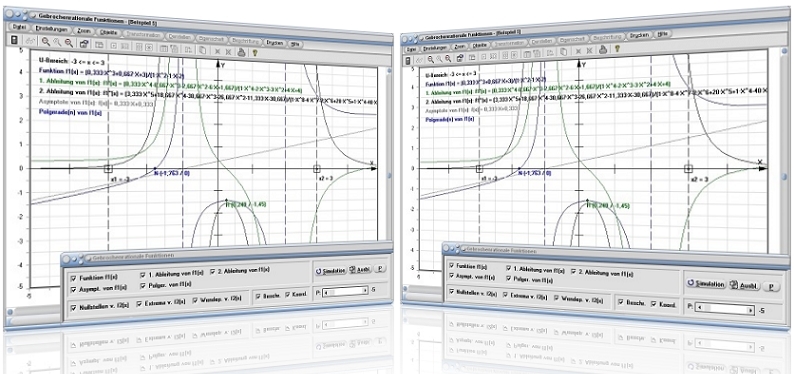
Modul Gebrochenrationale Funktionen

---

 
Das Unterprogramm [Analysis] - [Ganz- und gebrochenrationale Funktionen] -  Gebrochenrationale Funktionen ermöglicht die Durchführung von Untersuchungen mit gebrochenrationalen Funktionen (Polynomgleichungen). Hierzu zählt u.a. die Durchführung der Polynomdivision und die Ermittlung evtl. vorhandener Pole (Unendlichkeitsstellen) und Asymptoten.

 

Funktionen die als Quotient zweier Polynome f1(x) und f2(x) darstellbar sind, werden als gebrochenrationale Funktionen bezeichnet. Sie besitzen sowohl in ihrem Zähler wie auch in ihrem Nenner eine ganzrationale Funktion. Funktionen dieser Art sind auch unter den Bezeichnungen rationale Funktionen oder Bruchfunktionen bekannt.
 
In diesem Modul können Analysen mit einer, oder zwei gebrochenrationalen Funktionen f1(x) und f2(x) folgender Formen durchgeführt werden (Formeln):
 

 

 

(mit 0 ≤ m ≤ 100 und 0 ≤ n ≤ 100)
 

Des Weiteren besteht die Möglichkeit, den Zähler bzw. den Nenner einer zu untersuchenden gebrochenrationalen Funktion in Nullstellenform und somit mit g(x) = c·(x-x₁)·(x-x₂)· ... ·(x-x_n) bzw. h(x) = c·(x-x₁)·(x-x₂)· ... ·(x-x_n) zu definieren.

 

Hierbei werden u.a. ermittelt:
 

• Asymptote der Kurve der Funktion f1(x) (Senkrechte Asymptote - waagerechte Asymptote - Hüllkurve)
• Asymptote der Kurve der Funktion f2(x) (Senkrechte Asymptote - waagerechte Asymptote - Hüllkurve)
• Polgerade(n) (Pole, Polstellen) der Kurve der Funktion f1(x)
• Polgerade(n) (Pole, Polstellen) der Kurve der Funktion f2(x)
• Summe der Funktionen f1(x)+f2(x)
• Differenz der Funktionen f1(x)-f2(x)
• Differenz der Funktionen f2(x)-f1(x)
• Produkt der Funktionen f1(x)·f2(x)
• Quotient der Funktionen f1(x)/f2(x)

 
Ausgegeben wird ebenfalls:

• Resultat nach Durchführung einer Substitution f1(f2(x)) der Funktionen f1(x) und f2(x)

Zudem werden ermittelt:

• 1. Ableitung f1'(x) der Funktion f1(x)

• 2. Ableitung f1''(x) der Funktion f1(x)

• 1. Ableitung f2'(x) der Funktion f2(x)

• 2. Ableitung f2''(x) der Funktion f2(x)
  
  Auch erfolgt die Bestimmung der Nullstellen, Polstellen (Pole, Unendlichkeitsstellen), Hochpunkte, Tiefpunkte und Wendepunkte (Wendestellen) der gebrochenrationalen (rationalen) Funktion

 
Das Programm versucht auch alle auffindbaren reellen und komplexen Nullstellen, sowie Pole der entsprechenden Funktion f1(x) bzw. f2(x) im Bereich -∞ ≤ x ≤ ∞ zu ermitteln - unabhängig vom gewählten Untersuchungsbereich zur Durchführung einer Kurvendiskussion. Nullstellen können u. U. doppelt verhanden sein. Dies beruht auf der Tatsache, dass versucht wird alle zur Faktordarstellung der entsprechenden rationalen bzw. gebrochenrationalen Funktion erforderlichen Nullstellen numerisch zu ermitteln. Komplexe Nullstellen besitzen einen Imaginärteil, für welchen die Bezeichnung i verwendet wird.

Mit dem Begriff Polynomdivision wird ein Rechenverfahren beschrieben, bei dem ein Polynom durch ein weiteres dividiert wird. Hierbei resultiert ein Ganzteilpolynom sowie u.U. ein Restpolynom. Die Handhabung dieser Methode entspricht der in der Schule gelehrten schriftlichen Division von Zahlen mit Rest. Dieses Programm führt bei der Definition zweier Polynome eine derartige Division mit diesen durch und gibt das Ergebnis dieser Operation als Quotient f1(x)/f2(x) aus.

 

Hinweise:

Die Koeffizienten a_n bzw. b_n der Polynomfunktionen können als reelle Zahlenwerte oder als einfache, ganzzahlige Brüche definiert werden.

 

Textausgaben wie Fehler bei Ermittlung ... oder Fehler bei Durchführung ... beruhen im Allgemeinen darauf, dass die entsprechende Funktion aufgrund mathematischer Sachverhalte nicht ermittelt werden kann (es existieren keine Lösungen) und nicht auf Fehlern in verwendeten Algorithmen oder fehlerhaft durchgeführten Termdefinitionen.
 
 

 
Unendlichkeitsstellen bzw. Pole sind Definitionslücken gebrochenrationaler Funktionen der Form f1(x)/f2(x), bei welchen der Funktionswert dieser gegen +∞ bzw. -∞ strebt. In einer Stelle dieser Art ist f1(x₀) = 0 und f2(x₀) ≠ 0. Eine an einer derartigen Stelle errichtete Parallele zur y-Achse wird als Polgerade bezeichnet. Besitzt die Funktion an der Stelle f2(x₀) lediglich eine Polstelle, so wird diese als einfacher Pol bezeichnet. Sind an dieser Position hingegen mehrere Unendlichkeitsstellen vorhanden, so verfügt sie an dieser Stelle über eine mehrfache Polstelle. Verhält sich eine Funktion bei bei Annäherung an einen Pol beidseitig gleichartig, so liegt ein Pol ohne Vorzeichenwechsel vor, andernfalls handelt es sich um einen Pol mit Vorzeichenwechsel.

Nach der Zerlegung einer Funktion dieser Art in ein Zählerpolynom sowie ein Nennerpolynom, jeweils bestehend aus Linearfaktoren, liefern die im Zähler vorhandenen Linearfaktoren seine Nullstellen. Die im Nenner existierenden Linearfaktoren sind dessen Polstellen (Pole).
    
Ist der Grad des Nenners einer gebrochenrationalen Funktion der Form f1(x)/f2(x) größer als der Grad des Zählers derer, so wird die Funktion als echt gebrochen bezeichnet. Ist der Grad ihres Nenners (Nennergrad) hingegen kleiner oder gleich dem Grad des Zählers (Zählergrad), so lautet ihre Bezeichnung hingegen unecht gebrochen. Eine echt gebrochenrationale Funktion nähert sich bei x →∞ der Abszisse (der x-Achse bei y = 0). Unecht gebrochenrationale Funktionen werden mittels Polynomdivision in eine ganzrationale Funktion p(x) sowie eine echt gebrochenrationale Funktion r(x) zerlegt → f(x) = p(x) + r(x). Die Polynomfunktion y = p(x) ist die Asymptote der unecht gebrochenrationalen Funktion.
   
Unter einer Asymptote (Näherungsfunktion) wird eine Kurve verstanden, welcher sich der Graph einer Funktion im Unendlichen allmählich nähert. Die Distanz zwischen Kurve und Funktionsgraph vermindert sich hierbei stetig. Es werden folgende Arten von Asymptoten unterschieden:
 
- Waagerechte Asymptoten: Eine waagerechte Asymptote (horizontale Asymptote) ist eine Gerade, die parallel zur x-Achse des Koordinatensystems verläuft

- Senkrechte Asymptoten: Eine senkrechte Asymptote (vertikale Asymptote) ist eine Gerade, die parallel zur y-Achse des Koordinatensystems verläuft

- Schiefe Asymptoten: Eine schiefe Asymptote (schräge Asymptote) ist eine Gerade, die weder parallel zur x- noch zur y-Achse verläuft, sondern durch eine Geradengleichung beschrieben wird

- Kurvenförmige Asymptoten: Bei einer kurvenförmigen Asymptote handelt es sich um eine Kurve, die sich dem Graphen einer Funktion nähert
  

 

 

Untersuchen und darstellen lassen können Sie sich gebrochenrationale Funktionen, wenn Sie wie nachfolgend geschildert vorgehen:
 

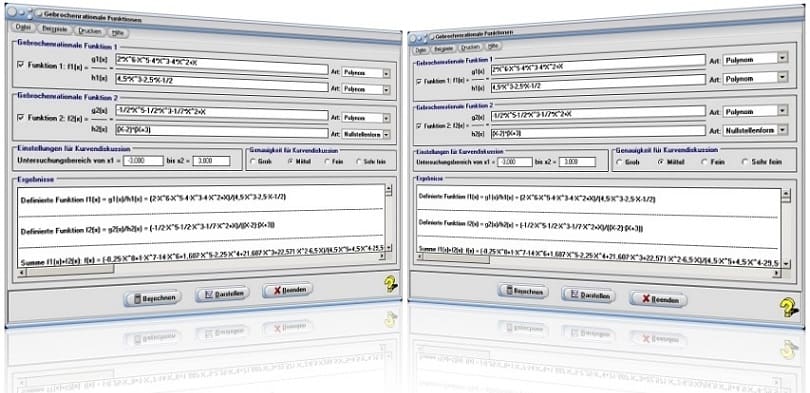
1. Aktivieren Sie das Kontrollkästchen Funktion 1 (voreingestellt). Definieren Sie die Terme des Zähler- und des Nennerpolynoms der Funktion f1(x) = g1(x)/h1(x) in den Eingabefeldern unter der Bezeichnung Funktion 1: f1(x) =.
   
   Ist zugleich eine zweite gebrochenrationale Funktion f2(x) = g2(x)/h2(x) zu untersuchen, so definieren Sie das entsprechende Zähler- und Nennerpolynom in den Feldern mit der Bezeichnung Funktion 2: f2(x) = und aktivieren das zugehörige Kontrollkästchen.
    
2. Wählen Sie durch die Selektion des Eintrags Polynom bzw. Nullstellenform aus der rechts neben dem entsprechenden Eingabefeld angeordneten Auswahlbox, ob eine Definition des jeweiligen Terms (des Zählers bzw. des Nenners der Funktion) in Form eines ganzrationalen Polynoms oder in Nullstellenform erfolgen soll.
    
3. Legen Sie im Formularbereich Einstellungen für Kurvendiskussion durch die Eingabe entsprechender Zahlenwerte den Bereich fest, innerhalb dessen eine Funktionsanalyse zur Ermittlung von Extrema und Wendepunkten durchgeführt werden soll (Untersuchungsbereich von x1 = und bis x2 =). Voreingestellt ist ein Untersuchungsbereich -3 £ x £ 3. Nullstellen werden unabhängig vom eingestellten Untersuchungsbereich ermittelt.
    
4. Durch die Aktivierung des Kontrollschalters Grob, Mittel, Fein oder Sehr fein legen Sie die zu verwendende Untersuchungsgenauigkeit zur Ermittlung von Extrema und Wendepunkten fest.
    
5. Nach einer Bedienung der Schaltfläche Berechnen werden die Resultate, soweit vorhanden bzw. ermittelbar, ausgegeben.
    
6. Klicken Sie auf die Schaltfläche Darstellen um sich die Zusammenhänge grafisch darstellen zu lassen.
    
7. Wählen Sie durch die Aktivierung des entsprechenden Kontrollkästchens auf dem Bedienformular die Kurve aus, die Sie sich darstellen lassen möchten. Zur Auswahl stehen:
   
   Funktion f1(x): Funktion f1(x) = g1(x)/h1(x)
   Funktion f2(x): Funktion f2(x) = g2(x)/h2(x)
   
   1. Ableitung von f1(x): 1. Ableitung f'(x) von Funktion f1(x)
   2. Ableitung von f1(x): 2. Ableitung f''(x) von Funktion f1(x)
   1. Ableitung von f2(x): 1. Ableitung f'(x) von Funktion f2(x)
   2. Ableitung von f2(x): 2. Ableitung f''(x) von Funktion f2(x)
   
   Asymptote von f1(x): Asymptote der Kurve der Funktion f1(x)
   Asymptote von f2(x): Asymptote der Kurve der Funktion f2(x)
   Polgerade(n) von f1(x): Polgerade(n) der Kurve der Funktion f1(x)
   Polgerade(n) von f2(x): Polgerade(n) der Kurve der Funktion f2(x)
   
   Summe f1(x)+f2(x): Summe der Funktionen f1(x)+f2(x)
   Subtraktion f1(x)-f2(x): Differenz der Funktionen f1(x)-f2(x)
   Subtraktion f2(x)-f1(x): Differenz der Funktionen f2(x)-f1(x)
   Produkt f1(x)·f2(x): Produkt der Funktionen f1(x)·f2(x)
   Quotient f1(x)/f2(x): Quotient der Funktionen f1(x)/f2(x)
   
   Substitution: Resultat nach Durchführung einer Substitution f1(f2(x)) der Funktionen f1(x) und f2(x)
    
8. Legen Sie durch die Aktivierung/Deaktivierung eines der Kontrollkästchen Nullstellen von f1(x) bzw. f2(x), Extrema von f1(x) bzw. f2(x) oder Wendep. von f1(x) bzw. f2(x) fest, ob eine Kurvendiskussion mit der entsprechenden Funktion durchgeführt werden soll.
   
   Möchten Sie den Untersuchungsbereich bei Durchführung einer Kurvendiskussion mit der Maus verändern, so klicken Sie in den rechteckig umrahmten Mausfangbereich einer Bereichsmarkierung und bewegen den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts (je schmaler der gewählte Bereich gewählt wird, desto exakter sind die resultierenden Berechnungsergebnisse).
    
9. Wurde eine Funktion deklariert, die das Einzelzeichen P zur Definition eines Funktionsparameters enthält, so definieren Sie den von ihm zu durchlaufenden Wertebereich und die gewünschte Schrittweite durch die Bedienung des Schalters P und positionieren Sie den Schieberegler P, um den Einfluss des Parameters zu untersuchen.
   
   Um eine automatisch ablaufende Parameterwertsimulation durchführen zu lassen, klicken Sie auf die Schaltfläche Simulation. Beendet werden kann die Ausführung dieser wieder durch eine erneute Betätigung derselben Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

 
Die bei der Durchführung interaktiver Kurvendiskussionen verwendeten Bezeichnungskürzel haben folgende Bedeutung:

 

Hinweis:

Der Parameter P kann in diesem Unterprogramm nur als einzelner Faktor, als Summand, oder als Zähler eines Bruchs verwendet werden. Eine Verwendung des Parametersymbols P in einer Form wie z.B. 1/P, 2*P, P/4 ist nicht zulässig und wird mit einer Fehlermeldung quittiert.

  

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden. Dieses Programm kann auch dabei behilflich sein, einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Wurde in den Eingabefeldern des Hauptformulars des Unterprogramms ein Term ohne Parameter P definiert, so wird ein den nachfolgend gezeigten Bildern ähnliches Bedienformular zur Verfügung gestellt, auf welchem Sie zusätzlich durch die Aktivierung der Kontrollkästchen entsprechende Einstellungen vornehmen können.

 

 
Enthält der erstellte Term das Einzelzeichen P zur Definition eines Funktionsparameters, so wird bei der Ausgabe einer grafischen Darstellung eines der nachfolgend abgebildeten Formulare eingeblendet.

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung des entsprechenden Kontrollkästchens folgende zusätzliche Einstellungen vornehmen:

• Beschriftung: Markierung und Nummerierung der mittels Kurvendiskussion ermittelten Punkte ein-/ausschalten
• Koordinaten: Anzeige der Koordinaten der mittels Kurvendiskussion ermittelten Punkte

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Gebrochenrationale Funktionen - Interaktiv

Mathematische Funktionen I

 

Beispiel 1 - Eine gebrochenrationale Funktion in Form eines Polynoms:

Gegeben sei die gebrochenrationale Funktion: f1(x) = (2·x⁶-x⁵-4·x³-4·x²+x) / (4·x³-2·x-3). Diese ist zu analysieren.
 

Vorgehensweise und Lösung:

 

Aus den rechts neben den obig positionierten zwei Eingabefeldern angeordneten Auswahlboxen wählen Sie jeweils den Eintrag Polynom. Aktivieren Sie das Kontrollkästchen Funktion f1(x) = (Kontrollkästchen Funktion f2(x) = bleibt deaktiviert), geben Sie die Zeichenfolge 2*X^6-X^5-4*X^3-4*X^2+X in das Feld g1(x) und die Zeichenfolge 4*X^3-2*X-3 in das Feld h1(x) ein und belassen Sie die Werte in den Eingabefeldern zur Kurvenuntersuchung auf den Vorgabeeinstellungen.

 

Nach einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:

Definierte Funktion f1(x) = g1(x)/h1(x) = (2·X^6-X^5-
4·X^3-4·X^2+X)/(4·X^3-2·X-3)

-------------------------------

1. Ableitung von f1(x):

 

f1'(x) = (24·X^8-8·X^7-20·X^6-28·X^5
+31·X^4+8·X^3+44·X^2+24·X-3)/
(16·X^6-16·X^4-24·X^3+4·X^2
+12·X+9)
 

-------------------------------

2. Ableitung von f1(x):

 

f1''(x) = (768·X^13-128·X^12-
1536·X^11-2048·X^10+992·X^9+
3360·X^8-640·X^7-4576·X^6-
480·X^5+2096·X^4+2268·X^3+
432·X^2+816·X+252)/(256·X^12
-512·X^10-768·X^9+384·X^8+
1152·X^7+736·X^6-576·X^5-
848·X^4-336·X^3+216·X^2

+216·X+81)
 

-------------------------------

Asymptote von f1(x): f(x) = 0,5·X^3-0,25·X^2+0,25·X-0,75

  -------------------------------

Nullstellen von f1(x):

Reelle Nullstellen:

N1 (-0,859 / 0)
N2 (0 / 0)
N3 (0,207 / 0)
N4 (1,635 / 0)

Komplexe Nullstellen:

N5 (-0,241 / -1,289 i)
N6 (-0,241 / 1,289 i)
 

-------------------------------

Pole von f1(x):

x1 = 1,09
 

-------------------------------

Extrema von f1(x) im Bereich von x1 = -3 bis x2 = 3:

H1 (-0,554 / 0,385)

T1 (0,104 / -0,018)
 

-------------------------------

Wendepunkte von f1(x) im Bereich von x1 = -3 bis x2 = 3:

W1 (-0,3 / 0,219)
W2 (1,716 / 0,43)
 
 

Beispiel 2 - Zwei gebrochenrationale Funktionen in Form von Polynomen:

Gegeben seien die gebrochenrationalen Funktionen f1(x) = (x⁷+x³+3·x²+x+1) / (5·x²-4·x-1) und f2(x) = (-x⁴+x³-3·x²+x-1) / (3·x²-5·x-1). Diese sind auf deren individuelle und gemeinsame Eigenschaften hin untersuchen zu lassen.

 

Vorgehensweise und Lösung:
 

Aus allen rechts neben den Eingabefeldern angeordneten Auswahlboxen wählen Sie den Eintrag Polynom. Aktivieren Sie die Kontrollkästchen Funktion f1(x) = und Funktion f2(x) =. Geben Sie die Zeichenfolge X^7+X^3+3*X^2+X+1 in das Feld g1(x) und die Zeichenfolge 5*X^2-4*X-1 in das Feld h1(x) ein. Belegen Sie die Eingabefelder g2(x) und h2(x) mit den Termen

-X^4+X^3-3*X^2+X-1 und 3*X^2-5*X-1.

 

Belassen Sie die Werte in den Eingabefeldern zur Kurvenuntersuchung auf den Vorgabeeinstellungen, so gibt das Programm nach einem Klick auf die Schaltfläche Berechnen aus:

 

Definierte Funktion f1(x) = g1(x)/h1(x) = (X^7+X^3+3·X^2+X+1)/
(5·X^2-4·X-1)
 

-------------------------------

Definierte Funktion f2(x) = g2(x)/h2(x) = (-X^4+X^3-3·X^2+X-1)/
(3·X^2-5·X-1)
 

-------------------------------

Summe f1(x)+f2(x):

 

f(x) = (3·X^9-5·X^8-1·X^7-5·X^6+
12·X^5-14·X^4+3·X^3-11·X^2-
3·X)/(15·X^4-37·X^3+12·X^2
+9·X+1)
 

-------------------------------

Differenz f1(x)-f2(x):

 

f(x) = (3·X^9-5·X^8-1·X^7+5·X^6
-6·X^5+22·X^4-29·X^3+1·X^2-
9·X-2)/(15·X^4-37·X^3+12·X^2+
9·X+1)
 

-------------------------------

Differenz f2(x)-f1(x):

 

f(x) = (-3·X^9+5·X^8+1·X^7-
5·X^6+6·X^5-22·X^4+29·X^3-
1·X^2+9·X+2)/(15·X^4-37·X^3+
12·X^2+9·X+1)
 

-------------------------------

Produkt f1(x)·f2(x):

 

f(x) = (-1·X^11+1·X^10-3·X^9
+1·X^8-2·X^7-2·X^6-1·X^5-
8·X^4-5·X^2-1)/(15·X^4-
37·X^3+12·X^2+9·X+1)
-------------------------------

Quotient f1(x)/f2(x):

 

f(x) = (3·X^9-5·X^8-1·X^7+
3·X^5+4·X^4-13·X^3-5·X^2-
6·X-1)/(-5·X^6+9·X^5-
18·X^4+16·X^3-6·X^2+3·X+1)
 

-------------------------------

Substitution f1(f2(x)):

 

f(x) = (-1·X^28+7·X^27-42·X^26+
168·X^25-588·X^24+1659·X^23-
4179·X^22+9024·X^21-17700·X^20
+31086·X^19-50586·X^18+
71838·X^17-82537·X^16+
60232·X^15+
3786·X^14-102232·X^13+
233407·X^12-
389598·X^11+422674·X^10-
180070·X^9-
106539·X^8+103730·X^7+
28399·X^6-17703·X^5-
20428·X^4-7424·X^3-
1542·X^2-143·X-7)/
(5·X^8-10·X^7+
47·X^6-72·X^5+108·X^4
-78·X^3+36·X^2-36·X)
 

-------------------------------

1. Ableitung von f1(x):

 

f1'(x) = (25·X^8-24·X^7-7·X^6+
5·X^4-8·X^3-20·X^2-16·X+3)/
(25·X^4-40·X^3+6·X^2+8·X+1)

-------------------------------

2. Ableitung von f1(x):

 

f1''(x) = (2500·X^11-6800·X^10+
4390·X^9+1520·X^8-1120·X^7-
448·X^6+1018·X^5+472·X^4-
+1688·X^3+272·X^2-76·X-40)/
(625·X^8-2000·X^7+1900·X^6-
80·X^5-554·X^4+16·X^3+
76·X^2+16·X+1)
 

-------------------------------

1. Ableitung von f2(x):

 

f2'(x) = (-6·X^5+18·X^4-6·X^3+
9·X^2+12·X-6)/(9·X^4-30·X^3+
19·X^2+10·X+1)

-------------------------------

2. Ableitung von f2(x):

 

f2''(x) = (-54·X^8+360·X^7-828·X^6+
282·X^5+342·X^4+888·X^3-
696·X^2+246·X+72)/(81·X^8
-540·X^7+1242·X^6-960·X^5
-221·X^4+320·X^3+138·X^2+
20·X+1)

-------------------------------

Asymptote von f1(x): f(x) = 0,2·X^5+
0,16·X^4+0,168·X^3+0,166·X^2+
0,367·X+0,927

-------------------------------

Asymptote von f2(x): f(x) = -0,333·X^2
-0,222·X-1,481

-------------------------------

 

Nullstellen von f1(x):

Reelle Nullstellen:

N1 (-1,122 / 0)

Komplexe Nullstellen:

N2 (-0,443 / 1,04 i)
N3 (-0,443 / -1,04 i)
N4 (-0,111 / 0,598 i)
N5 (-0,111 / -0,598 i)
N6 (1,115 / 0,801 i)
N7 (1,115 / -0,801 i)

-------------------------------

Nullstellen von f2(x):

Komplexe Nullstellen:

N1 (0,148 / -0,633 i)
N2 (0,148 / 0,633 i)
N3 (0,352 / -1,499 i)
N4 (0,352 / 1,499 i)

-------------------------------

Pole von f1(x):

x1 = -0,2
x2 = 1

-------------------------------

Pole von f2(x):

x1 = -0,18
x2 = 1,847
-------------------------------

Extrema von f1(x) im Bereich von x1 = -3 bis x2 = 3:

H1 (0,156 / -0,821)

T1 (1,397 / 6,739)

-------------------------------

Wendepunkte von f1(x) im Bereich von x1 = -3 bis x2 = 3:

W1 (-0,777 / 0,272)

-------------------------------

Extrema von f2(x) im Bereich von x1 = -3 bis x2 = 3:

H1 (-0,756 / -0,941)
H2 (2,901 / -7,16)

T1 (0,387 / 0,413)

-------------------------------

Wendepunkte von f2(x) im Bereich von x1 = -3 bis x2 = 3:

Keine Wendepunkte gefunden
 
 

Beispiel 3 - Eine gebrochenrationale Funktion in Nullstellenform:

Gegeben sei die gebrochenrationale Funktion: f1(x) = ((x+1)·(x-3/5)·(2·x-1))/ ((x-2)·(x+3)). Es gilt diese zu untersuchen.
 

Vorgehensweise und Lösung:

 

Aus den rechts neben den obig positionierten zwei Eingabefeldern angeordneten Auswahlboxen wählen Sie den Eintrag Nullstellenform. Aktivieren Sie das Kontrollkästchen Funktion f1(x) = (Kontrollkästchen Funktion f2(x) = bleibt deaktiviert), geben Sie die Zeichenfolge (X+1)*(X-3/5)*(2*X-1) in das Feld g1(x) und die Zeichenfolge (X-2)*(X+3) in das Feld h1(x) ein und belassen Sie die Werte in den Eingabefeldern zur Kurvenuntersuchung auf den Vorgabeeinstellungen.

 

Nach einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:

Definierte Funktion f1(x) = g1(x)/h1(x) = ((X+1)·(X-3/5)·(2·X-1))/((X-2)·(X+3))

-------------------------------

1. Ableitung von f1(x): f1'(x) = (2·X^4+4·X^3-34,6·X^2+1,2·X+9)/
(1·X^4+2·X^3-11·X^2-12·X+36)

-------------------------------

2. Ableitung von f1(x): f1''(x) = (25,2·X^5-50,4·X^4+151,2·X^3+
806,4·X^2-2293,2·X+151,2)/(1·X^8+
4·X^7-18·X^6-68·X^5+145·X^4+
408·X^3-648·X^2-864·X+1296)

-------------------------------

Asymptote von f1(x): f(x) = 2·X-2,2

-------------------------------

Nullstellen von f1(x):

Reelle Nullstellen:

N1 (-1 / 0)
N2 (0,5 / 0)
N3 (0,6 / 0)

-------------------------------

Pole von f1(x):

x1 = -3
x2 = 2

-------------------------------

Extrema von f1(x) im Bereich von x1 = -3 bis x2 = 3:

H1 (0,551 / 0,002)

T1 (-0,483 / -0,176)

-------------------------------

Wendepunkte von f1(x) im Bereich von x1 = -3 bis x2 = 3:

W1 (0,068 / -0,083)
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6
   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Rationale Funktion
Wikipedia - Kurvendiskussion
Wikipedia - Ableitung
Wikipedia - Nullstelle
Wikipedia - Extremwert

 

 

 

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

 

Startfenster des Unterprogramms Gebrochenrationale Funktionen
 

MathProf 5.0 - Unterprogramm Ganzrationale Funktionen - Interaktiv

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---