PhysProf - Hookesches Gesetz - Poisson-Zahl - Scherung - Torsion

Fachthemen: Hookesches Gesetz - Feder - Elastizität - Kompression
PhysProf - Mechanik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Veranschaulichung der Zusammenhänge, welche durch das Hookesche Gesetz beschrieben werden.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul: |
 |  |
Hookesches Gesetz
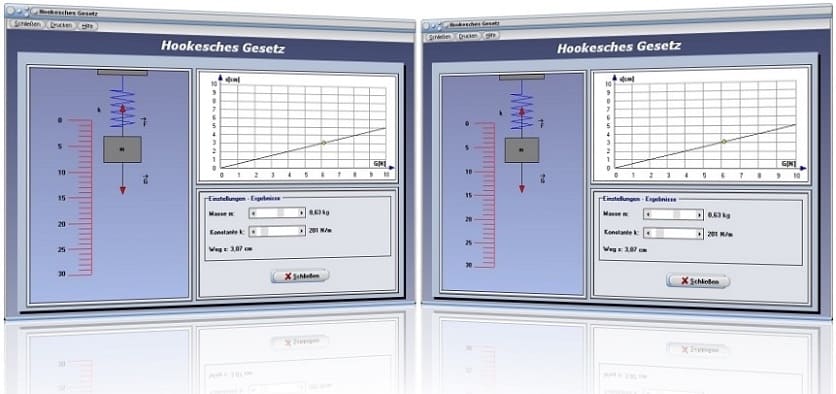
Modul Hookesches Gesetz
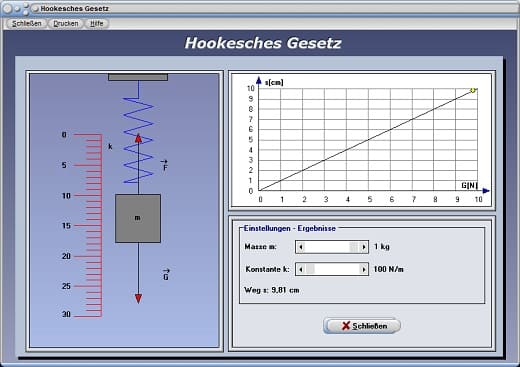
Das Programmmodul [Mechanik II] - [Hookesches Gesetz] erlaubt es, Zusammenhänge bzgl. der Federkraft zu analysieren.

Hookesches Gesetz - Abbildung 1

Hookesches Gesetz - Abbildung 2
Das Hookesche Gesetz (Federgesetz) besagt, dass sich die auf eine Feder wirkende Kraft proportional zur Verformung dieser verhält. Eine der meist genutzten Federarten ist die Schraubenfeder. Diese besteht aus einem langen Metallstück, welches um sich selbst gewickelt ist. Kräfte können durch Zug- und Druckwirkung die Form eines Körpers verändern.
Innerhalb der Elastizitätsgrenze eines Materials verhalten sich Kraft und Deformierung proportional. Als Richtgröße hierfür wird der sogenannte Proportionalitätsfaktor verwendet, welcher bei Federn speziell als Federkonstante bezeichnet wird. Die Federkonstante wird auch als Federsteifigkeit, Federhärte oder Federrate bezeichnet. Für sie gilt:

Die Reaktionskraft, welche an der Feder angreift, heißt Federkraft oder auch Federspannkraft (Spannkraft). Je härter eine Feder ist, desto größer ist die Federkonstante und somit die Federsteifigkeit. Sie wird beschrieben durch:
F = -k·s
Hierbei sind:
k: Federkonstante [N/m]
F: Kraft, welche die Länge der Feder ändert [N]
s: Federweg [m]
Der Wert der Federkonstante (Direktionskonstante), auch als Federhärte, Federsteifigkeit oder Federrate bezeichnet, hängt nicht nur von der Dimensionierung und Auslegung der Feder ab, sondern zudem vom Material, aus welchem sie besteht. Sie gibt an, in welchem Maß sich eine belastete Feder (in Metern) ausdehnt, wenn sie mit einem Gewicht (in Newton) belastet wird. Sie bezieht sich auf das Material aus dem sie gefertigt wurde sowie auf dessen Herstellungsart.
Der Federweg (die Auslenkung der Zugfeder) erteilt Auskunft darüber, um welches Maß sich eine Zugfeder verlängert, wenn sie mit einem Gewicht belastet wird. Die Hookesche Gerade kann als lineare Relation zwischen der wirkenden Federkraft und der daraus resultierenden Längenänderung ∆l der Feder interpretiert werden.
Federkraftmesser (auch als Kraftmesser bezeichnet) sind mechanische Messgeräte die die Dehnung einer Feder zur Messung der auf sie einwirkenden Kraft (zur Kraftmessung) anwenden.
Bei einer Zugfeder handelt es sich um eine aus Stahl bestehende Feder, die auf Zug belastbar ist und aus eng beieinander liegenden Drähten geformt ist.
Programmbedienung
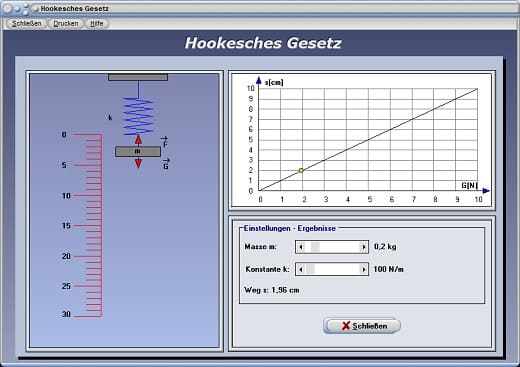
Mit Hilfe der Darstellung dieses Unterprogramms können Sie sich die Gültigkeit des Hookeschen Gesetzes für eine Feder anhand der Darstellung eines symbolisch dargestellten Federkraftmessers veranschaulichen. Hierbei ist es möglich, die Masse m des angehängten Körpers, wie auch die Konstante k mit Hilfe der zur Verfügung stehenden Rollbalken zu verändern. Das Verhalten einer Feder hinsichtlich ihrer Auslenkung in Abhängigkeit von der ihr angehängten Masse und ihrer Federkonstante kann dem Kraft-Weg-Diagramm (F-s-Diagramm) entnommen werden..
Hierbei ist zu erkennen, dass sich bei der gegebenen Federkonstante k die Auslenkung der Feder proportional zum Gewicht des angehängten Körpers verhält.
Unter einer statischen Kraft wird eine Kraft verstanden, welche an einem ruhenden oder einem geradlinig bewegten Körper angreift. Von einer dynamischen Kraft wird gesprochen, wenn diese an einem sich nicht gleichförmig und nicht geradlinig bewegenden Körper wirkt.
Mit dem Begriff Dehnung (Ausdehnung) wird die relative Längenänderung eines stabförmigen Körpers beschrieben, wenn dieser einer Druck- oder Zugbelastung ausgesetzt wird. Deren Dimension ist anhängig von der Form des Körpers, seinem Material (seiner Temperatur) sowie von der auf ihn wirkenden Kraft. Spannung und Dehnung sind zueinander proportional. Die Zugspannung beschreibt die Belastung die ein Material hinsichtlich Zug erfährt. Sie wird in Pa (N/m²) angegeben.
Gemäß dem Hookeschen Gesetz gilt:
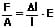
Der Elastizitätsmodul (Elastizitätskoeffizient, Zugmodul oder E-Modul bzw. E Modul) beschreibt das Verhältnis zwischen erforderlicher Spannung und erzielter Dehnung bei der Verformung eines festen Körpers. Für ihn gilt:
E = σ/ε
Es gilt: Die elastische Dehnung ε ist proportional zur einwirkenden Zugspannung σ.
Die Spannung ist definiert mit:
σ = F/A
E: Elastizitätsmodul [Pa]
σ: Spannung [Pa]
ε: Dehnung []
A: Querschnittsfläche [m²]
F: Wirkende Kraft [N]
Die bei einer Dehnung verursachte Längenänderung kann wie folgt berechnet werden:
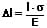
l: Ursprüngliche Länge des Stabs [m]
Δl: Längenänderung des Stabs [m]
σ: Spannung [Pa]
E: Elastizitätsmodul [Pa]
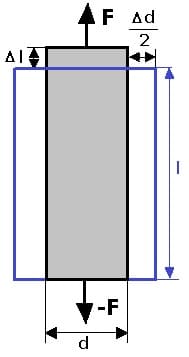
Durch die Dehnung eines Stabes (Körpers) ändert sich auch dessen Querschnittsfläche und sein Durchmesser. Es bestehen diesbezüglich folgende Zusammenhänge:
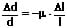
d: Ursprünglicher Durchmesser (ursprüngliche Breite) des Stabs [m]
Δd: Veränderter Durchmesser des Stabs [m]
l: Ursprüngliche Länge des Stabs [m]
Δl: Längenänderung des Stabs [m]
μ: Poisson-Zahl
Durch Kräfte ausgelöste Verformungen in Querrichtung die bei einem Wertstoff entstehen werden als Querdehnungen bezeichnet. Als Längsdehnungen werden derartige Verformungen bezeichnet, die in Längsrichtung auftreten.
Querkontraktion: Die Poissonzahl (Poissonsche Zahl, Querkontraktionszahl, Querdehnungszahl oder Querdehnzahl) μ gibt das Verhältnis Querdehnung/Längsdehnung an, welches durch eine Längenänderung eines Körpers unter dem Einfluss einer mechanischen Spannung verursacht wird. Sie ist eine Konstante (ein Materialkennwert), die vom Material des entsprechenden Körpers abhängig ist.
μ = Δd/d : Δl/l
Δd/d: Verhältnis der Längenänderung in Querrichtung
Δl/l: Verhältnis der Längenänderung in Längsrichtung
μ: Poisson-Zahl
Ein Spannungs-Dehnungs-Diagramm gibt Auskunft über die Eigenschaften Festigkeit und Elastiztät eines Materials. Jeder Werkstoff besitzt ein für ihn geltendes Diagramm dieser Art. Als Streckgrenze wird die Elastizitätsgrenze eines Werkstoffs bezeichnet, bei der bei einer einachsigen und momentenfreien Zugbeansruchung keine plastische Verformung auftritt. Der Werkstoff nimmt nach Durchführung einer Beanspruchung dieser Art wieder seine ursprüngliche Form an.
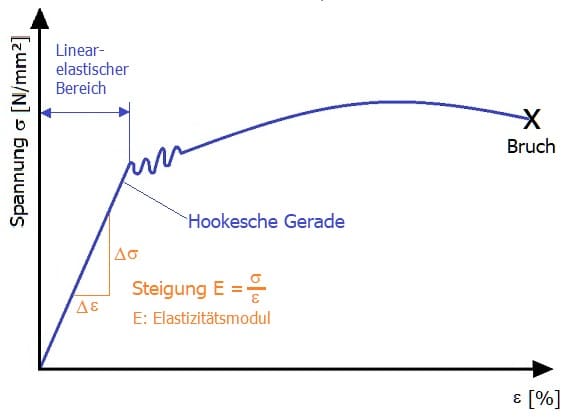
Abb.: Spannungs-Dehnungs-Diagramm
Ein Diagramm dieser Art wird in die folgenden wesentlichen Bereiche unterteilt:
I - Elastischer Bereich:
Dieser Bereich gliedert sich in den linear-elastischen und den nichtlinear-elastischen Teilbereich.
1. Linear-elastischer Bereich: Innerhalb dessen verläuft die Materialdehnung proportional zur Spannung und ist umkehrbar. Die Steigung der sich in diesem Abschnitt befindenden Strecke wird als Elastizitätsmodul (E-Modul) des entsprechenden Werkstoffs bezeichnet. Er berechnet sich wie folgt:
E = Δσ/Δε = tan φ
E: Elastizitätsmodul [Pa]
Δσ: Änderung der Spannung [Pa]
Δε: Änderung der Dehnung []
φ: Steigungswinkel der Strecke [rad]
2. Nichtlinear-elastischer Bereich: In diesem Bereich erfolgt keine proportionale Materialdehnung, dennoch ist diese umkehrbar.
II - Plastischer Bereich:
Eine in diesem Bereich durchgeführte Materialdehnung ist irreversibel und bedingt eine dauerhafte, plastische Verformung des Materials. Dieser plastische Bereich unterteilt sich in den Fließbereich, den Materialverfestigungsbereich sowie den Einschnürungsbereich.
1. Fließbereich: Innerhalb des Fließbereichs erfolgt bereits eine plastische Verformung des Materials, jedoch liegt trotz der zunehmenden Dehnung des Werkstoffs eine Schwankung der Spannungswerte vor.
2. Materialverfestigungsbereich: Innerhalb dieses Bereichs erfolgt aufgrund der Änderung der Gitterstruktur des Materials eine Schwächung des Kurvenanstiegs trotz einer zunehmenden Spannung.
3. Einschnürungsbereich: Durch die Bildung von Hohlräumen innerhalb der Gitterstruktur des Materials tritt eine Einschnürung in Richtung der Mitte des untersuchten Materials auf. Diese Einschnürung setzt sich bis zum Bruch des Materials stetig fort und es ist zur Durchführung einer Dehnung stets weniger Spannung erforderlich.
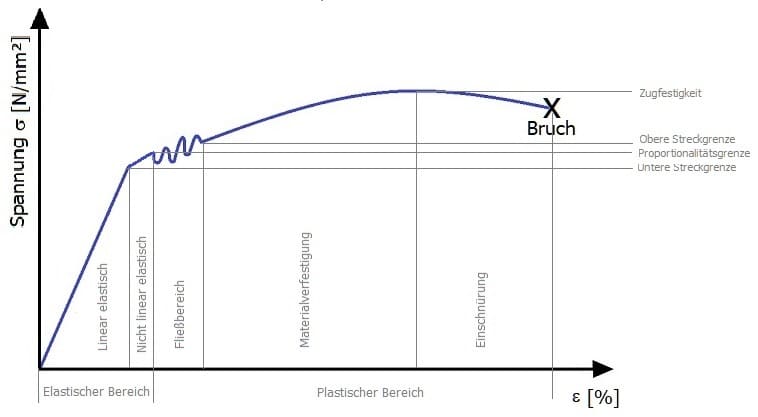
Abb.: Spannungs-Dehnungs-Diagramm - Bereiche
Linear elastisch: Beim Vorliegen einer linearen Elastizität verhalten sich die auftretenden Dehnungen proportional zu den wirkenden Spannungen. Dieser Zusammenhang wird auch als linear-elastisches Verhalten eines Materials bezeichnet.
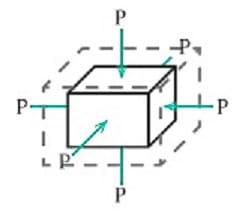
In der Physik wird unter Kompression das Verdichten (Zusammendrücken) von Körpern, Flüssigkeiten oder Gasen verstanden. Von einer Kompressibilität wird gesprochen, wenn durch einwirkende Druckveränderungen nennenswerte Dichteänderungen des Materials zu verzeichnen sind (meist lediglich bei Gasen).
Der Kompressionsmodul K gibt Auskunft darüber, in welcher Dimension eine allseitig wirkende Druckänderung vorzuliegen hat, um eine relative Volumenänderung zu bewirken. Er ist das Verhältnis einer notwendigen Druckänderung zu einer hervorgerufenen Volumenänderung. Sein Kehrwert wird als Kompressibilität bezeichnet.
Für die Kompression gilt:
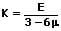
E: Elastizitätsmodul [Pa]
K: Kompressionsmodul [Pa]
μ: Poisson-Zahl
Für die Kompressibilität gilt:
κ = 1/K
κ: Kompressibilität [1/Pa]
K: Kompressionsmodul [Pa]
Volumenänderung:
Die durch Kompression verursachte Volumenänderung kann wie nachfolgend gezeigt berechnet werden:
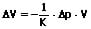
V: Volumen des Körpers [m³]
ΔV: Volumenänderung bei Druckveränderung [m³]
Δp: Druckänderung [Pa]
K: Kompressionsmodul [Pa]
Die elastische Verformung (elastische Formänderung) eines Körpers liegt vor, wenn dieser erneut seine ursprüngliche Form annimmt, nachdem die auf ihn bis dahin einwirkende Kraft nicht mehr wirksam ist. Für Verformungen dieser Art besitzt das Hookesche Gesetz Gültigkeit. Formänderungen dieser Art ergeben sich beispielsweise nach Krafteinwirkungen auf Gummi oder Schaumstoff.
Plastische Verformung (plastische Formänderung: Bei der plastischen Verformung (plastischen Formänderung) eines Körpers trifft dies nicht zu. Die Verformung eines Körpers ist plastisch, wenn er nach deren Umsetzung nicht wieder von alleine seine ursprüngliche Form annimmt. Derartige Formänderungen treten beispielsweise durch Krafteinwirkungen auf Metalle oder Knetwerkstoffe auf.
Bei der Verlängerung einer Feder um einen Weg s ist die dafür aufzubringende Arbeit nicht konstant. Sie wird als Federspannarbeit oder Spannarbeit bezeichnet, nimmt proportional mit s zu und wächst von 0 bis Fmax.
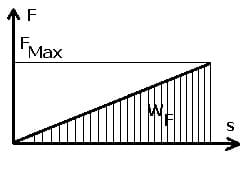
Als Verformungsarbeit (Federspannarbeit) wird eine mechanische Arbeit beschrieben, die verrichtet wird, wenn ein Körper verformt wird. Für sie gilt:
WF = k·s²/2
WF: Verformungsarbeit (Federspannarbeit) [J]
s: Federweg [m]
k: Federkonstante [N/m]
Die Spannenergie (elastische Energie) ist eine Form der potentiellen Energie und entspricht der Energie, die ein Körper (eine Feder) aufgrund seiner elastischen Verformung besitzt. Sie kann mittels dem Spannen einer Feder gespeichert werden und resultiert aus der Verformung einer Feder.
Für die Spannenergie gilt:
Es = k·s²/2
Es: Spannenergie [J]
s: Federweg [m]
k: Federkonstante [N/m]
Ein Federschwinger (Federpendel) besteht aus einer (vertikal angeordneten) elastischen Feder, an welcher eine Masse in Form eines Körpers befestigt ist und sich in auf- und abbewegt. Die Schwingungsdauer (Periodendauer) eines Federschwingers hängt von den elastischen Eigenschaften der Feder sowie von der Masse des ihr angehängten Körpers ab.
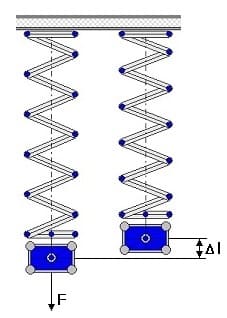
Bewegt sich die Feder innerhalb des elastischen Bereichs, so ist gemäß dem Hookeschen Gesetz die verformende Kraft proportional zur Verformung der Feder und sie führt eine harmonische Schwingung (lineare Federschwingung) aus. Wird der Federschwinger mehrmals aufeinanderfolgend ausgelenkt, so bewirken innere Reibungskräfte und der Luftwiderstand eine Dämpfung der Elongation (gedämpfte Schwingung).
Die Federkonstante besitzt den Wert:
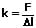
Für die Eigenfrequenz einer solchen Federschwingung gilt:
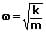
bzw.
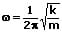
Die Schwingungsdauer einer derartigen linearen Schwingung kann wie folgt berechnet werden:
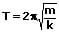
k: Federkonstante [N/m]
F: Wirkende Kraft [N]
Δl: Längenänderung der Feder [m]
m: Masse des angehängten Körpers [kg]
T: Schwingungsdauer [s]
f: Schwingungsfrequenz [1/s]
ω: Kreisfrequenz = 2πf [1/s]
Als Rückstellkraft FR wird diejenige Kraft bezeichnet, die einen harmonisch schwingenden Körper in Richtung der Ruhelage dieser Masse zieht. Für sie gilt allgemein:
FR = -ŷmω²sinφ = -ymω²
Die Rückstellkraft einer Feder kann näherungsweise wie folgt berechnet werden:
FR = -ks
Als Richtgröße wird das Verhältnis zwischen FR und y bezeichnet. Für sie gilt:
k = -FR/y = mω²
FR: Rückstellkraft [N]
m: Masse des schwingenden Körpers [kg]
y: Auslenkung [m]
ŷ: Amplitude der Auslenkung [m]
s: Federweg [m]
φ: Auslenkungswinkel [rad]
ω: Kreisfrequenz = 2πf [1/s]
Lineares Kraftgesetz:
Beim Vorliegen einer harmonischen Schwingung ist die rücktreibende Kraft eines Schwingungsystems proportional zu dessen Auslenkung. Findet die Anwendung des Hookeschen Gesetzes auf schwingende Körper statt, so wird vom linearen Kraftgesetz gesprochen. Somit gilt F ~ s und das lineare Kraftgesetz besitzt Gültigkeit.
Dieses lautet: F = -ks bzw. F = -ky
F: Wirkende Kraft [N]
s,y: Federweg [m]
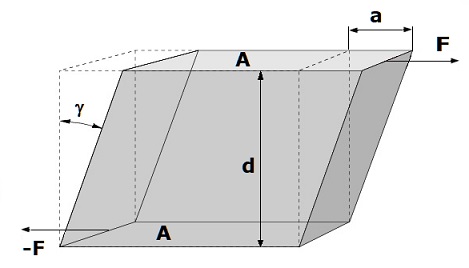
Scherung
Unter einer Scherung werden in der Geometrie der Ebene bestimmte affine Abbildungen der Ebene auf sich selbst verstanden, bei denen der Flächeninhalt erhalten bleibt. Eine Gerade der Ebene bleibt hierbei fix. Dies bedeutet, dass jeder Punkt dieser Gerade auf sich selbst abgebildet wird.
Es gilt entsprechend dem Hookeschen Gesetz:
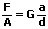
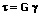
A: Fläche [m²]
F: Kraft (parallel zu A) [n]
τ: Schubspannung [N/m²]
γ: Schiebung (Scherung, Schubwinkel) [rad]
G: Schubmodul (Gleitmodul, Torsionsmodul) [N/m²]
a,d: Abstände [m] (tan(γ) ∼ a/d)
Es gilt: Schubspannung und Scherung (Schiebung) sind einander proportional.
Als Schubmodul wird das Verhältnis der erforderlichen Schubspannung zur erzielten Schiebung bezeichnet. Es gilt: G = 1/γ.
Als Schubkoeffizient wird der Kehrwert des Schubmoduls bezeichnet: Für ihn gilt: β = 1/G.
Der Schubmodul G kann auch aus den anderen Elastizitätskonstanten gebildet werden. Hierbei gilt:
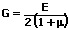
G: Schubmodul [N/m²]
E: Elastizitätsmodul []
μ: Poisson-Zahl []
Torsion
Entgegen der bei einer Scherung auftretenden Parallelverschiebung einzelner Schichten, erfolgt bei einer Torsion eine Verdrehung einzelner Schichten gegeneinander. Ein Ende des Zylinders wird entgegen dem festen Ende dessen mit der Wirkung eines Drehmoments M um den Drillwinkel α verdrillt.
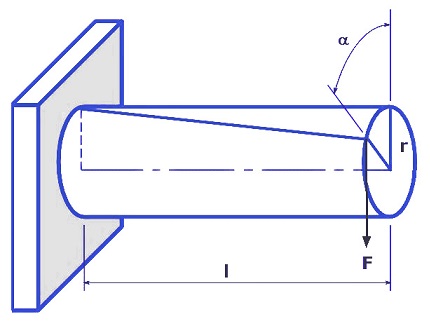
Es gilt:
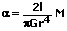
Es gilt: Drillwinkel α und Drehmoment M sind einander proportional.
Der Proportionalitätsfaktor ist das Richtmoment (die Winkelrichtgröße, das Direktionsmoment) D:
D = M/α
Somit gilt:
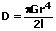
α: Drillwinkel [rad]
G: Torsionsmodul (Schubmodul) [N/m²]
l: Länge des Zylinders [m]
r: Radius des Zylinders [m]
M: Drehmoment [Nm]
D: Richtmoment [Nm]
In folgender Tabelle sind weitere Werte für den Elastizitätsmodul (Elastizitätskoeffizient) einiger Stoffe aufgeführt.
| Stoff | Elastizitätsmodul in GPa bei 20°C |
| Aluminium | 70 |
| Baustahl | 210 |
| Beryllium | 303 |
| Beton | 20...40 |
| Blei | 19 |
| Diamant | ca.1000 |
| Eis (−4 °C) | 10 |
| Glas | 40...90 |
| Gold | 78 |
| Gusseisen | 90 ...145 |
| Hartgummi | 5 |
| Holz | 10 ...15 |
| Keramik | 160 ... 440 |
| Kupfer | 100 ...130 |
| Magnesium | 44 |
| Marmor | 72 |
| Messing | 78...123 |
| Nickel | 195...205 |
| Polypropylen | 1,3...1,8 |
| PVC | 1,0 ... 3,5 |
| Titan | 110 |
| Wolfram | 405 |
| V2A-Stahl | 180 |
In folgender Tabelle sind weitere Werte für den Kompressionsmodul einiger Stoffe aufgeführt.
| Stoff | Kompressionsmodul in GPa bei 20°C |
| Aceton | 0,92 |
| Aluminium | 74 |
| Barium | 9,6 |
| Bismut | 31 |
| Blei | 46 |
| Bor | 320 |
| Borcarbid | 271 |
| Caesium | 1,6 |
| Diamant | 442 |
| Ethanol | 0,896 |
| Glas | 35...55 |
| Glycerin | 4,35 |
| Gold | 180 |
| Iod | 7,7 |
| Lithium | 11 |
| Magnesiumoxid | 277 |
| Methanol | 0,823 |
| Natrium | 6,3 |
| Öl | 1...1,6 |
| Osmium | 462 |
| Quecksilber | 28,5 |
| Platin | 271 |
| Rhodium | 380 |
| Rubidium | 2,5 |
| Stahl | 160 |
| Titan | 130 |
| Vanadium | 160 |
| Wasser | 2,08...2,68 |
| Zink | 58 |
| Zinn | 52,7 |
In folgender Tabelle sind weitere Werte der Poissonzahl (auch Poissonsche Zahl oder Querkontraktion) einiger Stoffe aufgeführt.
| Stoff | Poisson-Zahl |
| Aluminium | 0,35 |
| Beryllium | 0,032 |
| Beton | 0,2 |
| Blei | 0,44 |
| Bor | 0,21 |
| Eisen | 0,21…0,259 |
| Glas | 0,18…0,3 |
| Gummi | 0,5 |
| Holz | 0,035…0,67 |
| Kork | 0,00 |
| Kupfer | 0,35 |
| Lehm | 0,3 |
| Magnesium | 0,35 |
| Messing | 0,37 |
| Nickel | 0,31 |
| Plexiglas | 0,4 |
| Sand | 0,2 |
| Schaumstoff | 0,1…0,4 |
| Siliciumcarbid | 0,17 |
| Silicium | 0,22 |
| Stahl | 0,27 |
| Titan | 0,33 |
Hookesches Gesetz - Abbildung 3
Hookesches Gesetz - Abbildung 4
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Hookesches Gesetz zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz


4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit -
Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit
Unterprogramm Hookesches Gesetz

PhysProf 1.1 - Unterprogramm RLC-Kreis

MathProf 5.0 - Unterprogramm Kurven in Parameterform

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.















