MathProf - Mengenlehre - Mengenschreibweise - Schnittmenge - Menge

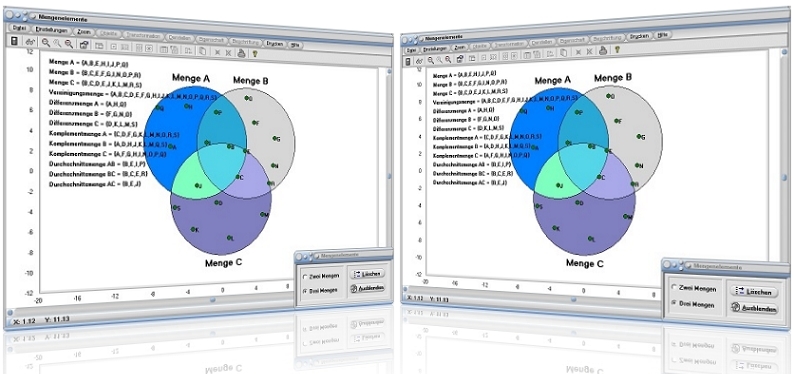
Modul Mengenelemente

---

 
Im kleinen Unterprogramm [Algebra] - [Mengen] - Mengenelemente können Untersuchungen zum Fachthemengebiet Mengenlehre durchgeführt werden.

 

In diesem Programmmodul zur Mengenlehre werden von einer Gesamtmenge ermittelt:
 

• Vereinigungsmenge

• Differenzmengen

• Komplementmengen

• Durchschnittsmengen

 

 

Wählen Sie durch die Aktivierung des Kontrollschalters Zwei Mengen bzw. Drei Mengen, ob Sie Untersuchungen mit zwei, oder drei Mengen durchführen möchten. Löschen Sie ggf. zuvor eingebundene Elemente durch die Benutzung der Schaltfläche Löschen.

 

Definieren Sie Mengenelemente durch einen Klick mit der linken Maustaste in die kreisförmig dargestellten Mengensymbole. Das Programm stellt diese in Form von Punkten dar und ermittelt hierauf unmittelbar die Ergebnisse für Differenzmengen, Komplementmengen sowie Durchschnittsmengen.
 

 
Menge (Mengenbegriff):

Eine Menge M ist eine Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens zu einem Ganzen. Diese Objekte heißen die Elemente der Menge. M={x ∈ N|E(x)}

Grundmenge:

Eine Grundmenge G setzt sich aus allen, in einem bestimmten mathematischen Zusammenhang betrachteten Objekten zusammen.

Leere Menge:

Eine leere Menge enthält kein Element, auch nicht die Null. Sie wiederum besitzt als einzige Teilmenge die leere Menge. M={}

Endliche Menge:

Eine Menge M ist genau dann endlich, wenn jede eindeutige Abbildung von M in sich eine eindeutige Abbildung auf M sein muss. f: M→{1,2,3,...,n}  n =|M|

Unendliche Menge:

Eine Menge ist genau dann unenedlich, wenn es eine eineindeutige Abbildung von M auf eine echte Teilmenge von M gibt. Eine Menge ist genau dann endlich, wenn sie nicht unendlich ist. f: M→{1,2,3,...,n} n=|M|

Abzählbare Menge:
 
Eine Menge M heißt abzählbar, wenn die Menge der natürlichen Zahlen zum Durchnumerieren der Elemente von M ausreicht. Dies bedeutet, dass eine eindeutige Abbildung von der Menge der natürlichen Zahlen auf M existiert.

Sätze:
Jede endliche Menge ist abzählbar
Jede unendliche Menge enthält eine abzählbar unendliche Teilmenge
Jede Teilmenge einer abzählbaren Menge ist abzählbar
Die Vereinigung abzählbar vieler abzählbarer Mengen ist wieder abzählbar
Die Menge der rationalen Zahlen Q ist abzählbar unendlich
Die Menge aller rellen Zahlen ist unabzählbar
Die Menge der natürlichen Zahlen ist abzählbar unendlich
 
Teilmenge (Teilmengenbeziehung):
 
Sind alle Elemente einer Menge M2 auch Elemente einer Menge M1, so nennt man M2 die Teilmenge von M1.

Echte Teilmenge:
 
Ist eine Menge M2 die Teilmenge einer Menge M1 und unterscheiden sich diese beiden Mengen, so wird von einer echten Teilmenge gesprochen.
 
Restmenge:

Die Menge aller Elemente die zur Menge M1, aber nicht zur Menge M2 gehören, nennt man Restmenge der Mengen M1 und M2.

Potenzmenge:

Als Potenzmenge wird die Menge aller möglichen Teilmengen einer gegebenen Grundmenge bezeichnet. P(M)={A∣ A⊆M}

Disjunkte Mengen:

Zwei Mengen M1 und M2 heißen disjunkt, wenn sie keine gemeinsamen Elemente besitzen.

Gleiche Mengen (Gleichheit zweier Mengen - Mengengleichheit):

Zwei Mengen M1 und M2 heißen gleich, wenn jedes Element von M2 auch Element von M1 ist und jedes Element von M1 auch Element von M2 ist. M1 = M2

Mächtigkeit (Kardinalität) von Mengen:

Ist eine Menge M endlich, so wird die Anzahl der Elemente als Mächtigkeit oder Ordinalzahl von M bezeichnet.

Gleichmächtige Mengen:
 
Zwei beliebige Mengen A und B sind zueinander gleichmächtig (A ~ B), wenn eine eineindeutige Abbildung von A auf B existiert. Die bedeutet, dass jedem Element der Menge A exakt ein Element der Menge B zugeordnet werden kann und jedem Element der Menge B genau ein Element der Menge A zugeordnet werden kann.

     

Nachfolgend sind wichtige Operationen der Mengenalgebra aufgeführt:
 
Durchschnittsmenge (Durchschnitt zweier Mengen):
 
Die Durchschnittsmenge (Schnittmenge) umfasst alle Elemente, die sowohl in Menge A, wie auch in Menge B enthalten sind.

A ∪ B = {x | x ∈ A und x ∈ B}

 

Vereinigungsmenge (Vereinigung zweier Mengen):
 
Die Vereinigungsmenge ist diejenige Menge, deren Elemente entweder in Menge A, oder in Menge B, oder in beiden Mengen enthalten sind.
A ∪ B = {x | x ∈ A oder x ∈ B}

 

Differenzmenge (Restmenge - Differenz zweier Mengen):
 
Die Differenzmenge umfasst alle Elemente, die zu einer Menge A gehören, jedoch nicht zu einer Menge B.

A \ B = {x | x ∈ A und x ∈ B}

 

Symmetrische Differenz:
 
Menge aller Elemente, die entweder in Menge A oder in Menge B, aber nicht in beiden Mengen enthalten sind.

A Δ B = (A \ B) ∈ (B \ A)

 

Komplementmenge:
 

Die Komplementmenge (Komplementärmenge) zu A umfasst alle Elemente, die nicht zu einer Menge A gehören.

¬A = {x | x ∉ A}

 

 

Kartesisches Produkt (Produktmenge, Paarmenge):
 
Das kartesische Produkt A × B zweier Mengen A und B ist die Menge aller geordneten Paare (a,b) wobei a ein Element der Menge A und b ein Element der Menge B ist (a ∈ A und b ∈ B).

Kleinstes Element - Größtes Element:
 
Ein Element einer geordneten Menge ist das größte Element der Menge, wenn alle anderen Elemente kleiner sind. Das kleinste Element einer Menge, ist das Element wenn alle anderen Elemente größer sind.
 

Nachfolgend sind Zusammenhänge (Gesetze) sowie gängige Zeichen (Symbole) der Mengenlehre aufgeführt:
 

Identitätsgesetz:

 

A ∪ A = A

A ∩ A = A

Durchschnitt und Vereinigung:
 

Die Mengenoperationen Durchschnitt und Vereinigung sind kommutativ, assoziativ und zueinander distributiv. Für sie gilt (De Morgansche Regeln bzw. Rechenregeln):

Kommutativtät:
 

 (A ∪ B) ∪ C = A ∪ (B ∪ C)

 (A ∩ B) ∩ C = A ∩ (B ∩ C)

Assoziativität:
 

A ∪ B = B ∪ A

A ∩ B = B ∩ A

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Distributivtät:
 

C (A ∪ B) = C A ∪ C B

C (A ∩ B) = C A ∩ C B

Differenzmengen:
 

Für die Differenzmengenbildung gilt:

 

(A \ B) \ C  = A \ (B ∪ C)

A \ (B \ C)  = (A \ B) ∪ (A ∩ C)

(A ∩ B) \ C = (A \ C) ∩ (B \ C)

(A ∪ B) \ C = (A \ C) ∪ (B \ C)

A \ (B ∩ C)  = (A \ B) ∪ (A \ C)

A \ (B ∪ C)  = (A \ B) ∩ (A \ C)

Symmetrische Differenz:
 

Für die symmetrische Differenz gilt:

 

(A Δ B) Δ C = A Δ (B Δ C)

A Δ B = B Δ A

(A Δ B) ∩ C = (A ∩ C) Δ (B ∩ C)

A Δ ∅ = A

A Δ A = ∅
 

 
Mengenlehre ist Lehrstoff der Grundschule wie auch am Gymnasium. Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf einfache Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthema.
 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben.

 

 

Venn-Diagramm

 

 

 

Nach einer Aktivierung des Kontrollschalters Drei Mengen und der Ausführung von acht Klicks in die kreisförmig dargestellten Mengensymbole, gemäß oben gezeigtem Muster, gibt das Programm aus:

 

Alle zur Menge A (gelb) gehörenden Elemente: Menge A = {A,B,C,E,H}

Alle zur Menge B (grau) gehörenden Elemente: Menge B = {B,C,G}

Alle zur Menge C (rot) gehörenden Elemente: Menge C = {C,D,F,H}

 

Vereinigungsmenge: {A,B,C,D,E,F,G,H}

(Menge deren Elemente entweder in Menge A, oder in Menge B, oder in beiden Mengen enthalten sind)

 

Differenzmenge: A = {A,E}

(Menge aller Elemente, welche zu Menge A gehören, jedoch nicht zu Menge B und nicht zu Menge C)

 

Differenzmenge: B = {G}

(Menge aller Elemente, welche zu Menge B gehören, jedoch nicht zu Menge A und nicht zu Menge C)

 

Differenzmenge: C = {D,F}

(Menge aller Elemente, welche zu Menge C gehören, jedoch nicht zu Menge A und nicht zu Menge B)

 

Komplementmenge: A = {D,F,G}

(Menge aller Elemente, welche nicht zu Menge A gehören)

 

Komplementmenge: B = {A,D,E,F,H}

(Menge aller Elemente, welche nicht zu Menge B gehören)

 

Komplementmenge: C = {A,B,E,G}

(Menge aller Elemente, welche nicht zu Menge C gehören)

 

Durchschnittsmenge: AB = {B,C}

(Menge aller Elemente, die sowohl in Menge A, wie auch in Menge B enthalten sind)

 

Durchschnittsmenge: BC = {C}

(Menge aller Elemente, die sowohl in Menge B, wie auch in Menge C enthalten sind)

 

Durchschnittsmenge: AC = {C,H}

(Menge aller Elemente, die sowohl in Menge A, wie auch in Menge C enthalten sind)
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3

   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

  

MathProf 5.0 - Unterprogramm Venn-Diagramm

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---