MathProf - Tangente - Normale - Gleichung - Tangentengleichung

 

Modul Tangente - Normale

---

Das Unterprogramm [Analysis] - [Tangente - Normale - Sekante] - Tangente - Normale stellt eine Ergänzung zum Unterprogramm Kurvendiskussion dar, bietet Einblick in die Differentialgeometrie und ermöglicht u.a. die Ermittlung (Berechnung) der Tangente und Normale einer Funktion bei einem bestimmten Abszissenwert (grafisches Ableiten).

Die Differentialgeometrie untersucht Kurven und Flächen mit Hilfe der Differentialrechnung. Jeder stetigen Funktion entspricht eine stetige Kurve und jeder differenzierbaren Funktion entspricht eine glatte Kurve.

 

Mit Hilfe dieses Moduls ist es u.a. möglich, sich die Werte für Folgendes ermitteln zu lassen:
 

• Funktionswert an Stelle Px (Qx)
• Steigungswinkel der Tangente in Punkt P (Q) (Tangentenwinkel)
• Wert der 1. Ableitung der Funktion in Punkt P (Q) (Tangentensteigung - Steigung der Tangente)
• Gleichung der durch Punkt P (Q) verlaufenden Tangente (Tangentengleichung)
• Abstand der durch Punkt P (Q) verlaufenden Tangente zum Koordinatenursprung
• Nullstelle der durch Punkt P (Q) verlaufenden Tangente

• Steigungswinkel der Normale (Normalensteigung) in Punkt P (Q)
• Gleichung der durch Punkt P (Q) verlaufenden Normale (Normalengleichung)
• Abstand der durch Punkt P (Q) verlaufenden Normale zum Koordinatenursprung
• Nullstelle der durch Punkt P (Q) verlaufenden Normale

• Eigenschaften des durch Punkt P (Q) verlaufenden Krümmungskreises
• Krümmung der Kurve in Punkt P (Q)  

 

Tangente - Normale - Tangentengleichung - Normalengleichung

Mit dem Begriff Tangente wird eine Gerade bezeichnet, welche die Kurve einer Funktion in einem bestimmten Berührpunkt P(x₀;y₀) berührt. Die Nullstelle einer Tangente ist derjenige Punkt bei dem diese Gerade die Abszisse (x-Achse) schneidet. Als Tangentengleichung wird die Gleichung bezeichnet, die die Steigung einer Tangente (Tangentensteigung) beschreibt. Sie besitzt die nachfolgend gezeigte Gestalt und lautet:



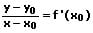
Tangentensteigung (Steigung der Tangente in einem Punkt): Die Steigung (der Anstieg) m_t der Tangente einer Funktion in einem Punkt P(x₀,y₀) und somit an der Stelle x₀ kann wie folgt berechnet werden:
 

 
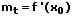
Die momentane Änderungsrate oder lokale Änderungsrate einer Funktion entspricht der Steigung der Tangente am Graphen dieser in einem bestimmten Punkt. Mit ihrer Hilfe kann die Steigung einer Kurve an jedem ihrer Punkte ermittelt werden
 
Eine Normale ist eine Gerade, die durch diesen Berührpunkt verläuft und vertikal (im Winkel von 90°) zur Tangente steht. Sie wird auch als das Lot zur Tangente oder Orthogonale zur Tangente bezeichnet. Die Nullstelle einer Normale ist der Punkt P(x₀;y₀) bei dem diese Gerade die Abszisse (x-Achse) schneidet. Sie besitzt die Steigung (Normalensteigung) m_n. Die Normalengleichung lautet:



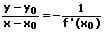
Normalensteigung: Die Steigung der Normale einer Funktion an einer Stelle x₀ berechnet sich wie folgt:

f'(x₀): 1. Ableitung f'(x) der Funktion f(x) an der Stelle x₀


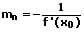
Steigungswinkel einer Tangente: Sofern es sich um keine vertikale Gerade (Senkrechte) handelt, gilt für den Steigungswinkel (den Anstiegswinkel) α einer Tangente, welche die Form y = mx + b besitzt:

tan(α) = Gegenkathete / Ankathete = m
 

Allgemeine Tangentengleichung: Eine Tangente die die Form f(x) = mx + b besitzt, wird als allgemeine Tangentengleichung bezeichnet.

Eine Funktion besitzt an einer Stelle x = x₀ eine waagerechte Tangente (horizontale Tangente), wenn an dieser Stelle die erste Ableitung dieser Funktion verschwindet und die Bedingung f'(x₀) = 0 erfüllt wrid.

Eine senkrechte Tangente (vertikale Tangente) an eine Kurve existiert in einem Punkt, an dem die Steigung der entsprechenden Funktion nicht definiert ist (unendlich ist).
 
 

 

Um eine explizit definierte Funktion an einer oder zwei verschiedenen Stellen untersuchen zu lassen, sollten Sie Folgendes ausführen:
 

1. Definieren Sie den entsprechenden Funktionsterm im dafür vorgesehenen Eingabefeld mit der Bezeichnung f(x) =. Beachten Sie hierbei die geltenden Syntaxregeln.
    

2. Legen Sie die Abszissenwerte der zu untersuchenden Stellen Px und Qx in den dafür zur Verfügung stehenden Eingabefeldern fest (zu untersuchende Stellen).
    

3. Nach einem Klick auf die Schaltfläche Berechnen werden die ermittelten Ergebnisse in der Tabelle ausgegeben.
    
4. Wählen Sie durch die Aktivierung des Kontrollkästchens Beide Stellen (Px und Qx) untersuchen aus, ob die Ausgabe der grafischen Darstellung lediglich für die Untersuchung an Stelle Px, oder an beiden Stellen (Px und Qx) erfolgen soll.
    
5. Bestimmen Sie durch die Aktivierung des Kontrollkästchens Zu untersuchende Stellen (Px bzw. Qx) verw., ob die Untersuchungen an den unter Einstellungen festgelegten Stellen durchgeführt werden sollen.
   
   Wird dieses nicht aktiviert, so stellt das Unterprogramm ein Bedienformular zur Verfügung, mit welchem eine Untersuchung innerhalb eines vorgegebenen Bereichs -10 ≤ x ≤ 10 durch die Positionierung eines Rollbalkens durchgeführt werden kann. Die im Formularbereich Einstellungen defnierten Werte für die Untersuchungsstellen Px und Qx werden hierbei ignoriert. Beim Aufruf der Darstellung verwendet das Programm in diesem Fall stets den Startwert Px = 0, für Qx den Startwert Qx = 2.
    
6. Bedienen Sie die Schaltfläche Darstellen.
    
7. Wurde auf dem Hauptformular des Unterprogramms das Kontrollkästchens Zu untersuchende Stellen (Px bzw. Qx) verw. aktiviert und möchten Sie während der Ausgabe der Darstellung die Abszissenwerte der im Hauptformular des Unterprogramms festgelegten Untersuchungspunkte P bzw. Q festlegen, so können Sie die Schaltfläche Punkt(e) auf dem Bedienformular nutzen und den, bzw. die entsprechenden Wert(e) im daraufhin erscheinenden Formular eingeben. Übernommen werden diese, wenn Sie die sich dort befindende Schaltfläche Ok bedienen.
    
8. Ist das Kontrollkästchen Zu untersuchende Stellen (Px bzw. Qx) verw.auf dem Hauptformular dieses Moduls deaktiviert worden, so kann durch eine Bedienung der Rollbalken x-Pos. Punkt P und x-Pos. Punkt Q eine Untersuchung des Verlaufs von Funktionstangenten bei bestimmten Abszissenpositionen innerhalb eines vorgegebenen Bereichs -10 ≤ x ≤ 10 analysiert werden.
   
   Um Abszissenpositionen simulativ verändern zu lassen, klicken Sie auf die Schaltfläche Simulation. Vor Ausführung einer Simulation wird Ihnen ein Formular zur Verfügung gestellt. Führen Sie hierauf ggf. notwendige Einstellungen durch und bestätigen Sie mit OK. Beendet werden kann die Ausführung einer Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

 
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Fachbitur (Fachabi) im Mathe-Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
 
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Wurde auf dem Hauptformular des Unterprogramms das Kontrollkästchen Zu untersuchende Stellen (Px bzw. Qx) verw. aktiviert und bleibt das Kontrollkästchen Beide Stellen (Px und Qx) untersuchen deaktiviert, oder wurden beide Kontrollkästchen aktiviert, so wird nachfolgend gezeigtes Bedienformular zur Verfügung gestellt.

 

 

Ist auf dem Hauptformular des Unterprogramms das Kontrollkästchens Beide Stellen (Px und Qx) untersuchen aktiviert worden und bleibt das Kontrollkästchen Zu untersuchende Stellen (Px bzw. Qx) verw. deaktiviert, so wird nachfolgend gezeigtes Bedienformular eingeblendet.

 

 

Sind auf dem Hauptformular des Unterprogramms die Kontrollkästchens Beide Stellen (Px und Qx) untersuchen und Zu untersuchende Stellen (Px bzw. Qx) verw. deaktiviert worden, so blendet das Programm nachfolgend gezeigtes Bedienformular ein.

 

 

Durch die Aktivierung der entsprechenden Kontrollkästchen lassen sich in allen Fällen darstellen:
 

• 1. Ableitung: 1. Ableitung der definierten Funktion f(x)

• Normale: Die durch Punkt P (Q) verlaufende Normale

• Krümmungskreis: Der durch Punkt P (Q) verlaufende Krümmungskreis
   

Hinweise

Achten Sie bei unstetigen Funktionen darauf, dass eine zu untersuchende Stelle innerhalb des Definitionsbereichs der Funktion liegt, da ansonsten keine Differenziation durchgeführt werden kann.

Das Laden und Speichern von Darstellungen wird in diesem Unterprogramm nur ermöglicht, wenn vor Ausgabe der grafischen Darstellung das Kontrollkästchen Beide Stellen (Px und Qx) untersuchen aktiviert ist und das Kontrollkästchen Zu untersuchende Stellen (Px bzw. Qx) verw. deaktiviert ist, oder wenn beide dieser Kontrollkästchen aktiviert sind.

 

Um Krümmungskreise nicht oval (ellipsenförmig) dargestellt zu bekommen, wählen Sie bei Ausgabe der grafischen Darstellung den Menüpunkt Einstellungen - Auflösung - Skalierungsart - Linear.
 

Analytische Ermittlung von Ableitungen

Unter dem Menüpunkt Ableitung analytisch können Sie sich die 1. Ableitung der definierten Funktion f(x) symbolisch differenziert ausgeben lassen. Es erscheint ein Formular.

1. Definieren Sie die Funktion, gemäß den geltenden Syntaxregeln, im Eingabefeld mit der Bezeichnung Y = f(x) =.
    
2. Nach der korrekten Deklaration der Funktion im Eingabefeld und der Bedienung des Schalters Ermitteln wird die 1. Ableitung der eingegebenen Funktion ermittelt und in den entsprechenden Ausgabefeldern angezeigt.

Ist die Funktionsdeklaration zu komplex um eine Ableitung symbolisch differenzieren zu können, so erscheint der Eintrag 'Funktion zu komplex - nicht differenzierbar' in den Ausgabefeldern.

Durch die Bedienung der dortigen Schaltfläche Schließen, kehren Sie wieder zum Unterprogramm zurück.

Hinweis:

Beinhaltet eine Funktionsdeklaration den Parameter P, so erhalten Sie eine Fehlermeldung, da parameterhaltige Funktionen nicht analytisch differenziert werden können.

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Mathematische Funktionen II

Tangente – Sekante

Tangente und Normale von externem Punkt

Kurvendiskussion

 

 

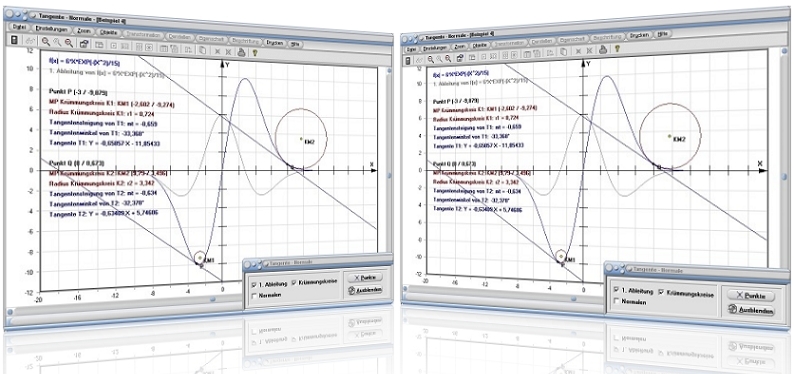
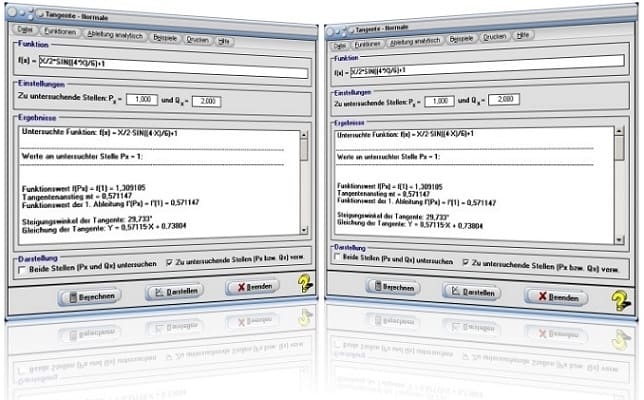
Es gilt, Untersuchungen (grafisches Ableiten) mit der Funktion f(x) = x/2·sin(x/5) an den Stellen Px = 1 und Qx = 2 durchführen zu lassen.

 

Vorgehensweise und Lösung:

 

Nach der Eingabe des Terms X/2*SIN(X/5) in das Feld f(x) =, der Festlegung der o.a. Koordinatenwerte in den Feldern Px = und Qx = sowie einer Bedienung des Schalters Berechnen erhalten Sie folgende Ergebnisse:

 

Werte an untersuchter Abszissenposition x = 1 (Stelle Px = 1):

Funktionswert: f(Px) = f(1) = 0,099335
Tangentenanstieg (Tangentensteigung): mt = 0,197335
Funktionswert der 1. Ableitung: f'(Px) = f'(1) = 0,197341

Steigungswinkel der Tangente: 11,163°
Gleichung der Tangente (Tangentengleichung): Y = 0,19734·X - 0,09801

Abstand der Tangente zum Koordinatenursprung (0|0): 0,096152
Nullstelle der Tangente: (0,496635 / 0)

Steigungswinkel der Normale (Normalensteigung): -78,837°
Gleichung der Normale (Normalengleichung): Y = -5,06736·X + 5,1667

Abstand der Normale zum Koordinatenursprung (0|0): 1,000311
Nullstelle der Normale: (1,019603 / 0)

Mittelpunkt des Krümmungskreises: MK (-0,0676 / 5,5094)
Radius des Krümmungskreises: rk = 5,5144

Krümmung der Kurve in Punkt P: kr = 0,1813

 
Werte an untersuchter Stelle Qx = 2 (Stelle Qx = 2):
 
Funktionswert: f(Qx) = f(2) = 0,389418
Tangentenanstieg (Tangentensteigung): mt = 0,378921
Funktionswert der 1. Ableitung: f'(Qx) = f'(2) = 0,378921

Steigungswinkel der Tangente (Tangentenwinkel): 20,753°
Gleichung der Tangente (Tangentengleichung): Y = 0,37892·X - 0,36848

Abstand der Tangente zum Koordinatenursprung (0|0): 0,34452
Nullstelle der Tangente: (0,972298 / 0)

Steigungswinkel der Normale (Normalenwinkel): -69,247°
Gleichung der Normale (Normalengleichung): Y = -2,63907·X + 5,66756

Abstand der Normale zum Koordinatenursprung (0|0): 2,008221
Nullstelle der Normale: (2,147559 / 0)

Mittelpunkt des Krümmungskreises: MK (-0,562 / 7,1507)
Radius des Krümmungskreises: rk = 7,2305

Krümmung der Kurve in Punkt Q: kr = 0,1383
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6
    

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden:

Wikipedia - Tangente
Wikipedia - Ableitung
   

 

 

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

 

Startfenster des Unterprogramms Tangente - Normale
 

MathProf 5.0 - Unterprogramm Kurvendiskussion - Interaktiv

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---