PhysProf - Beugung - Spalt - Gitter - Leuchtdichte - Lichtstärke - Lichtstrom
Fachthemen: Beugung am Spalt - Lichtbeugung - Licht - Strahlung - Auflösung
PhysProf - Optik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen zur Begleitung des Physikunterrichts und des Unterrichts naturwissenschaftlicher Fächer sowie für alle die sich für Physik interessieren. Zur effektiven Benutzung dessen wird ein bereits erlangtes Grundwissen zum entsprechenden Themengebiet vorausgesetzt.
Online-Hilfe für das Modul
zur Darstellung und Auswertung von Zusammenhängen, welche beim Auftreffen von Lichtwellen an Spalten gelten.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte und eignet sich zudem als Begleitung zu Versuchen im Physikunterricht.
Es können Untersuchungen zur Beugung am Einzelspalt, zum Doppelspaltexperiment sowie zur Beugung am Gitter durchgeführt werden.
Hierbei unterstützt es, ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul:Beugung - Beugung am Spalt - Beugung am Einzelspalt - Beugung am Doppelspalt - Beugung am Gitter - Wellenoptik - Physikalische Optik - Einfachspalt - Mehrfachspalt - Wellenlänge - Minima - Maxima - Doppelspalt - Doppelspaltexperiment - Gitterkonstante - Beugungswinkel - Spaltbreite - Intensitätsverteilung - Intensität - Intensitätsmaxima - Beugungsmaxima - Beugungsmuster - Beugungsbild - Berechnen - Formel - Formelzeichen - Rechner - Simulation - Animation - Graphen - Was - Wie - Weshalb - Was ist - Warum - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Beschreibung - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Einheit - Physikalische Einheit - Licht - Optisches Gitter - Lichtwellen - Doppelspaltversuch - Definition - Gleichung - Lambda - Minimum - Maximum - Spalt - Spalte - Gitter - Extrema - Lichtbeugung - Diffraktion - Elementarwelle - Elementarwellen - Ablenkung - Ablenken - Schattenraum - Kante - Lichtbeugung am Gitter - Interferenzstreifen - Interferenzmaxima - Interferenzminima - Interferenzmaximum - Interferenzminimum - Transmissionsgitter - Reflexionsgitter - Interferenzbedingung - Interferenzen - Interferenz von Wellen - Interferenzmuster - Interferenz am Doppelspalt - Destruktive Interferenz - Konstruktive Interferenz - Beugungsordnung - Optische Gitter - Gittergleichung - Hauptmaximum - Nebenmaximum - Hauptmaxima - Nebenmaxima - Beugungsgitter - Gesetzmäßigkeiten - Verändern - Veränderung - Ändern - Änderung - Gangunterschied - Interferenz - Wirkung - Einzelspalt - Lichtstrahl - Lichtstrahlen - Strahl - Strahlen - Strahlenbündel - Helligkeit - Beugung von Wellen - Wellen - Huygenssches Prinzip - Huygens - Prinzip - Bedingung - Spaltabstand - Apertur - Öffnungsweite - Berechnung - Physik - Unterricht - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Einführung - Aufgaben - Abituraufgaben - Lösungen - Versuch - Physikalisch - Ablauf - Abläufe - Untersuchen - Analyse - Vorgang - Vorgänge - Darstellen - Bild - Grafik - Grafische Darstellung - Lichtstrahlung - Strahlung - Strahlungsfluss - Strahlungsleistung - Bestrahlung - Bestrahlungsstärke - Strahlstärke - Strahlungsintensität - Strahlungsstärke - Spezifische Ausstrahlung - Ausstrahlungsstromdichte - Abstrahlungsstärke - Strahldichte - Strahlungsdichte - Leuchtdichte - Lichtstrom - Lichtstärke - Lumen - Candela - Raumwinkel - Lichtausstrahlung - Lichtmenge - Beleuchtung - Beleuchtungsstärke - Lux - Belichtung - Luxsekunde - Solarkonstante - Lichtausbeute - Ausstrahlungswinkel - Abstrahlwinkel - Strahlungswinkel - Numerische Apertur - Auflösungsgrenze - Auflösungsvermögen - Auflösung - Abbe-Limit - Abbe Grenze - Fernrohr - Mikroskop - Lambertsches Gesetz - Lambert-Beersches Gesetz - Extinktion - Extinktionskoeffizient - Absorptionskoeffizient |
 |  |
Beugung am Spalt - Lichtstrahlung - Auflösung
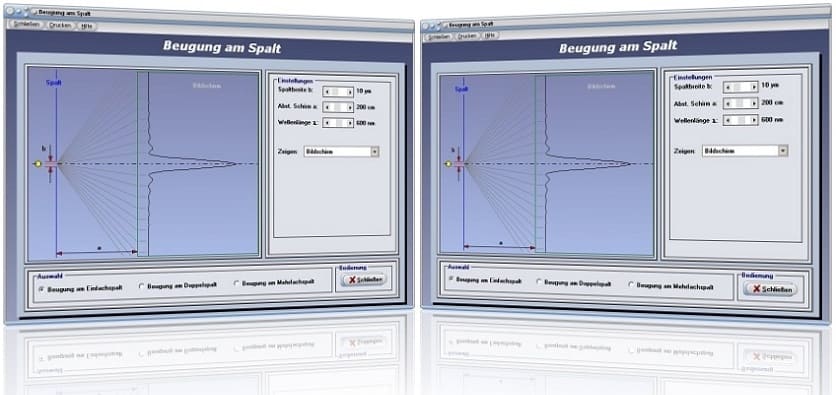
Modul Beugung am Spalt
Mit Hilfe des Unterprogramms [Optik] - [Beugung am Spalt] können Zusammenhänge analysiert werden, welche beim Auftreffen von Lichtwellen an Spalten auftreten.
Beugung am Einfachspalt
Beugung am Einfachspalt - Funktionsverlauf
Beugung am Doppelspalt
Beugung am Doppelspalt - Funktionsverlauf
Beugung am Mehrfachspalt
Beugung am Mehrfachspalt - Funktionsverlauf
Mit dem Begriff Wellenoptik (physikalische Optik) wird in der Physik der Teilbereich der Optik bezeichnet, in welchem Licht in Form elektormagnetischer Wellen behandelt wird. Sie wird zur Beschreibung der Eigenschaften des Lichts eingesetzt. Hierzu zählen neben dessen Farbe, der Überlagerung (Interferenz) seiner Wellen unter anderem die Beugung sowie die Polarisation dessen.
Licht, welches an scharfen Kanten vorbeiläuft, wird gebeugt. Unter Lichtbeugung (Diffraktion) wird die Ablenkung eines Lichtstrahls an einem Hindernis (einer Kante) verstanden. Zur Beugung (Ablenkung) dessen kommt es, da sich diese Wellen im geometrischen Schattenraum des Hindernisses (Spalt, Gitter) nicht vollständig eliminieren können. Es entstehen sogenannte Interferenz-Erscheinungen.
Hinsichtlich der Untergliederung verschiedener Arten der Beugung am Spalt wird unterschieden zwischen der Beugung am Einfachspalt (Beugung am Einzelspalt), der Beugung am Doppelspalt und der Beugung am Gitter. Auf diese Beugungsarten wird in einem nachfolgenden Kapitel eingegangen.
Das Huygenssche Prinzip besagt, dass jeder Punkt einer ebenen Wellenfront die auf einen Spalt trifft, die Ausgangsposition einer weiteren Elementarwelle ist. Interferenzen von Wellen, die hinter einem Einzelspalt (Einfachspalt) auftreten, können bei derem Auftreffen auf einem Bildschirm als Interferenzmuster oder Interferenzstreifen interpretiert werden. Hierbei entstehen sogenannte Interferenzminima sowie Interferenzmaxima.
Doppelspaltexperiment - Doppelspaltversuch: Bei der Durchführung des Doppelspaltexperiments (Doppelspaltversuchs) wird zusammenhängendes (monochromatisches) Licht auf eine Blende gelenkt, die über zwei schmale, eng beieinander positionierte, parallel angeordnete Spalte verfügt. Der Abstand der Lichtquelle zum Doppelspalt ist erheblich größer als der Abstand dieser beiden Spalte. Hinter dieser Blende befindet sich ein Bildschirm, auf welchem ein Interferenzmuster zu sehen ist, das sich aus unterschiedlich hellen Streifen zusammensetzt. Dieses bildet sich aufgrund der Überlagerung der Lichtwellen, die durch diese beiden Öffnungen gelangen. Auf dem Schirm kann die Intensitätsverteilung des Lichts analysiert und mit Hilfe des Huygenschen Prinzips berechnet werden.
Dieses Experiment lässt sich auch mit Elektronen, Neutronen, Photonen und Atomen durchführen. Auch hierbei zeigt sich dass hinsichtlich der Eigenschaften von Wellen und Teilchen unter bestimmten Bedingungen dieselben Sachverhalte vorliegen.
Optische Gitter sind periodische Strukturen die zur Beugung von Licht eingesetzt werden. Als Beugungsgitter (optisches Gitter oder Mehrfachspalt) wird die Anordnung einer Reihe eng beieinander positionierter, parallel angeordneter Spalten bezeichnet. Wie auch beim Einzel- oder Doppelspalt kommt es hierbei zu einer Beugung (Ablenkung von Wellen an einem Hindernis) des Lichts und einer Interferenz (Überlagerung) der Wellen deren Muster auf einem Schirm abgebildet werden kann.
Zur Messung von Lichtwellenlängen kommen keine Doppel- oder Mehrfachspalte zum Einsatz. Vielmehr werden Transmissionsgitter und Reflexionsgitter verwendet. Transmissionsgitter sind Beugungsgitter, bei denen Licht durch das Gitter hindurchdringt und eine Reflexion an deren Oberfläche weitestgehend ausbleibt. Sie werden in Form von Metall- oder Glasplatten erzeugt, die über Rillen (Furchen) verfügen, die in gleichmäßigen Abständen eingeritzt werden. Reflexionsgitter besitzen eine spiegelnde Oberfläche die über eine gleichmäßig parallel angebrachte Gitterstruktur verfügen, wodurch das reflektierte Licht interferiert.
Bei einer Gittergleichung handelt es sich um eine Gleichung, die die Position der Interferenzmaxima bei der Beugung von Wellen hinter einem Doppelspalt oder einem Beugungsgitter beschreibt (siehe Beugung).
Bei einer Elementarwelle handelt es sich um eine Welle, die sich kugel- oder kreisförmig um ihr Zentrum ausbreitet.
Als Schattenraum wird der vom Schatten eines Objekts erfüllte Raum bezeichnet, in den kein Licht gelangen kann.
Unter dem Fachbegriff Gangunterschied wird der Abstand (Wegunterschied) zweier oder mehrerer kohärenter Wellen verstanden.
Mit dem Begriff Strahlenbündel wird eine Anzahl einzelner Strahlen (Lichtstrahlen, Teilchenstrahlen) bezeichnet, die exakt oder beinahe parallel zueinander verlaufen.
Lichtwellen werden gemäß dem Huygensschen Prinzip an den Kanten von Spalten gebeugt. Hierbei kommt es zur Überlagerung entstehender Elementarwellen. Das dabei entstehende Muster wird als Beugungsmuster oder Beugungsbild bezeichnet.
Interferenz - Interferenzmuster - Bedingungen
Unter dem Begriff Interferenz wird die Überlagerung von Wellen verstanden.
Destruktive Interferenz:
Bei einer destruktiven Interferenz (destruktiven Überlagerung) entspricht der Gangunterschied zweier Wellen einem geradzahligen Vielfachen derer halber Wellenlänge λ/2 (es resultiert gegenphasiges Schwingen). Besitzen beide Wellen dieselbe Amplitude, so führt dies zu einer Auslöschung der Gesamtamplitude (Minimum).
Konstruktive Interferenz:
Entspricht der Gangunterschied zweier Wellen einem geradzahligen ganzzahligen Vielfachen derer Wellenlänge λ (lambda), so handelt es sich um eine konstruktive Interferenz (konstruktive Überlagerung). Besitzen beide Wellen dieselbe Amplitude, so führt dies zu einer Verdoppelung der Gesamtamplitude (Maximum).
Beugung - Spalt - Doppelspalt - Gitter
Die nachfolgend verwendete Variable k wird als Beugungsordnung bezeichnet. Mit zunehmender Beugungsordnung nimmt die Intensität der Beugungsmaxima ab.
I - Beugung am Einfachspalt (Einzelspalt):
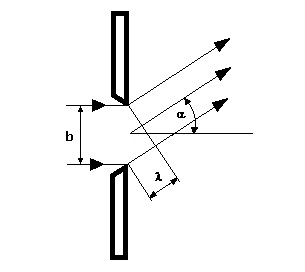
An den Kanten eines engen Spaltes bilden sich nach dem Huygensschen Prinzip der Elementarwellen. Je nach Richtung besteht zwischen diesen ein bestimmter Gangunterschied, bei welchem bei der Überlagerung Maxima oder Minima resultieren.
Intensitätsminima treten auf für:
Intensitätsmaxima treten auf für:
(mit k = 0, ± 1, ± 2, ...)
Hierbei liegt das Hauptmaximum in der ursprünglichen Richtung des Lichts (bei α = 0). Nebenmaxima besitzen eine wesentlich geringere Intensität, welche sich mit wachsendem k stets verringert.
II - Beugung am Doppelspalt:
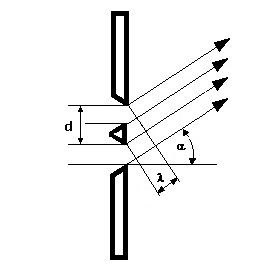
Liegen zwei Spalte dicht beieinander, so spricht man von Doppelspalt. Bei einem Doppelspalt liegen ähnliche Verhältnisse vor. Zur Interferenz gelangen jeweils entsprechende Strahlen beider Spalte. Je nach Gangunterschied entstehen Maxima oder Minima.
Hierbei gilt für Intensitätsminima:
Für Intensitätsmaxima gilt:
(mit k = 0, ± 1, ± 2, ...)
III - Beugungsgitter (Beugung am Gitter):
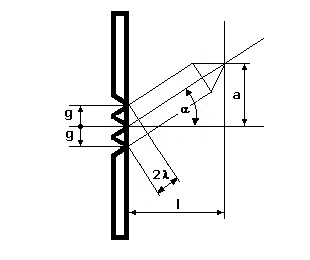
Sind in regelmäßigen Abständen mehrere oder viele Spalte angeordnet, so wird von einem Beugungsgitter gesprochen. Der zwischen einzelnen Spalten bestehende Abstand wird als Spaltabstand bezeichnet. Hierbei auftretende Beugungserscheinungen entsprechen prinzipiell den am Doppelspalt auftretenden. Durch die hohe Zahl der parallel nebeneinander liegenden Spalte sind Maxima jedoch deutlich heller. Den Abstand zweier Spalte bezeichnet man als Gitterkonstante g. Je größer die Gitterkonstante g und je kleiner die Wellenlänge λ ist, desto weiter entfernen sich die Beugungsmaxima voneinander. Es gilt:
(mit k = 0, ± 1, ± 2, ...)
Je kleiner die Gitterkonstante g ist, desto größer ist der Beugungswinkel für eine bestimmte Wellenlänge.
Für alle drei zuvor beschriebenen Fälle gilt:
Die Spaltbreite sowie die Wellenlänge beeinflussen die Position der Maxima und Minima. Der Beugungswinkel vergrößert sich bei zunehmender Wellenlänge. Eine Beugung tritt erstmalig dann ein, wenn die Spaltbreite kleiner oder gleich der Wellenlänge des Lichts ist.
αmin: Beugungswinkel für Richtung der Minima [rad]
αmax: Beugungswinkel für Richtung der Maxima [rad]
λ: Wellenlänge [m]
b: Spaltbreite [m]
d: Abstand zweier Spalte [m]
g: Gitterkonstante
k: Beugungsordnung der Maxima und Minima
Programmbedienung
Mit diesem Unterprogramm können Sie die Auswirkung einzelner Parameteränderungen der Einflussgrößen auf die o.a. Zusammenhänge untersuchen.
An den dargestellten Spaltöffnungen wird ein einfallender Lichtstrahl um einen Winkel α abgelenkt. Benutzen Sie die zur Verfügung stehenden Rollbalken Spaltbreite b, Abst. Schirm a, Wellenlänge λ und ändern Sie die Werte der Größen Spaltbreite, Schirmabstand (bzw. Spaltabstand) und Wellenlänge. Die Darstellung wird hierauf aktualisiert.
Je größer die Wellenlänge des einfarbigen Lichts ist, desto größer wird der Winkel α und die Maxima streben auseinander. Aus den Abständen einer derartigen Anordnung und der Interferenzstreifen kann die Wellenlänge des verwendeten Lichts berechnet werden.
Durch die Aktivierung des Kontrollschalters Einfachspalt, Doppelspalt oder Mehrfachspalt legen Sie zunächst fest, ob Sie die Analyse für einen Einfachspalt, einen Doppel- oder Mehrfachspalt durchführen möchten.
Möchten Sie sich die Intensität in Form eines Funktionsverlaufs darstellen lassen, so wählen Sie aus der aufklappbaren Auswahlliste den Eintrag Funktionsverlauf. Hierauf wird die Intensitätskurve in einem kartesischen Koordinatensystem dargestellt. Das Programm gibt in diesem Fall zudem alle Maxima bzw. Minima der Kurve aus, welche innerhalb eines bestimmten Bereiches existieren.
Auch in diesem Fall können Sie die Werte der Einflussgrößen durch die Bedienung der dafür vorgesehenen Rollbalken einstellen. Zudem besteht die Möglichkeit, durch die Aktivierung des dafür vorgesehenen Kontrollkästchens Pos. der Extrema markieren, die ermittelten Extrema im Schaubild markieren zu lassen.
Auflösungsvermögen - Auflösungsgrenze
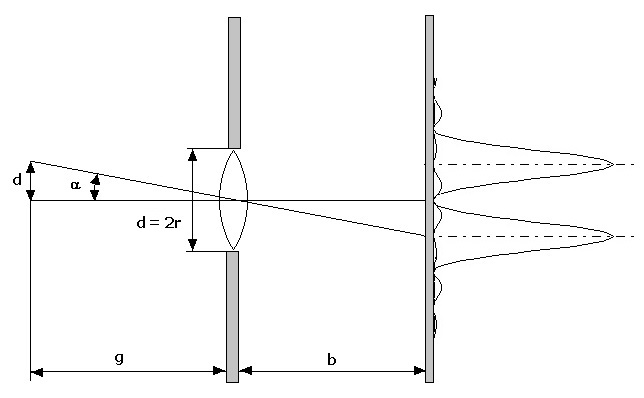
Unter dem Begriff Auflösungsvermögen wird in der Optik die Differenzierbarkeit von Bildpunkten verstanden. Von optischen Geräten und vom menschlichen Auge können einzelne Punkte von Gegenständen, abhängig von der Entfernung dieser vom entsprechenden Gegenstand, nicht als separate punktförmige Objekte identifiziert werden.
Als Auflösungsgrenze wird die Größe der durch das Auflösungsvermögen eines optischen Gerätes bestimmten Abbildungsqualität bezeichnet. Sie entspricht dem geringsten Abstand zweier Bildpunkte die noch optisch zu unterscheiden sind. Die Auflösungsgrenze des menschlichen Auges liegt bei ca. 1'.
Für die Auflösungsgrenze des menschlichen Auges sowie des Fernrohrs gilt:
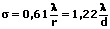
Für die Auflösungsgrenze eines Mikroskops gilt:
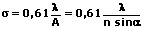
σ: Auflösungsgrenze
α: Halber Öffnungswinkel des Objektivs
λ: Wellenlänge des Lichts [m]
r: Radius der Öffnung [m]
d: Durchmesser der Öffnung [m]
n: Brechzahl (des Mediums zwischen Objektiv und Objekt)
Als Apertur oder Öffnungsweite wird in der Optik die Dimension einer Öffnung (der Durchmesser) bezeichnet, durch welche Lichtstrahlen gesendet oder empfangen werden.
Als numerische Apertur A wird der Faktor der Brechzahl des Mediums und des halben Öffnungswinkels des Objektivs bezeichnet. Es gilt:
A = n·sin(α)
Lichtstrahlung - Strahlungsfluss - Strahlungsleistung - Bestrahlung - Bestrahlungsstärke - Strahlungsstärke - Strahlungsintensität - Strahlungsdichte - Leuchtdichte - Lichtstärke - Lichtstrom - Lichtmenge - Beleuchtungsstärke - Belichtung
Ein Lichtstrahl beschreibt die geradlinige Ausbreitung des Lichts aus einer Lichtquelle. Nachfolgend aufgeführt sind einige grundlegende Zusammenhänge zum Fachthema Lichtstrahlung. Zudem sind relevante Formeln zu den Themen Licht und Strahlen angegeben.
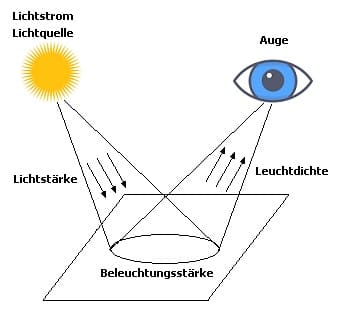
Ausstrahlungswinkel - Abstrahlwinkel - Strahlungswinkel:
Als Ausstrahlungswinkel (auch Abstrahlwinkel oder Strahlungswinkel genannt) wird der Öffnungswinkel des Lichtbündels einer Leuchte (Lampe) bezeichnet, mit dem Licht aus einer Strahlungsquelle austritt. Er wird durch die Bauart des verwendeten Reflektors bestimmt.
Strahlungsfluss:
Als Strahlungsfluss oder Strahlungsleistung Φe wird die je Zeiteinheit von einer Strahlungsquelle als Strahlung abgegebene Energie bezeichnet. Ist die Leistung je Zeiteinheit konstant, so gilt:
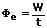
Φe: Strahlungsfluss [W]
W: abgegebene Energie [J]
t: Zeit [s]
Ist die Leistung je Zeiteinheit nicht konstant, so ergibt sich:
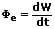
Bestrahlung:
Wird der Strahlungsfluss auf eine Fläche des Empfängers bezogen, so gilt für die gleichmäßige Bestrahlung He:
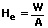
He: Bestrahlung [J/m²]
W: aufgenommene Energie [J]
A: Fläche des Empfängers [m²]
Bei einer ungleichmäßigen Bestrahlung gilt:
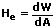
Bestrahlungsstärke:
Als Bestrahlungsstärke Ee wird die gesamte Leistung der eingehenden elektromagnetischen Energie bezeichnet, die auf eine Empfängerfläche Ae trifft. Sie bezieht sich auf die Fläche des Empfängers und es gilt bei einer gleichmäßigen Verteilung des Strahlungsflusses:
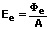
Ee: Bestrahlungsstärke [W/m²]
W: eingehende Energie [J]
Ae: Fläche des Empfängers [m²]
Liegt eine ungleichmäßige Verteilung des Strahlungsflusses vor, so gilt:
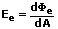
Strahlungsstärke:
Als Strahlungsstärke (Strahlstärke) oder Strahlungsintensität Ie wird die von einer Strahlungsquelle in einer gegebenen Raumrichtung abgestrahlte Leistung bezeichnet. Für sie gilt:
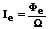
Ie: Strahlstärke [W/sr]
Φe: Strahlungsfluss [W]
Ω: Raumwinkel [sr]
Ist der Strahlungsfluss innerhalb der Raumrichtung nicht gleichmäßig verteilt, so gilt:
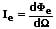
Spezifische Ausstrahlung:
Als spezifische Ausstrahlung (Ausstrahlungsstromdichte bzw. Abstrahlungsstärke) wird die elektromagnetische Strahlungsleistung dΦe bezeichnet, die von einem Oberflächenelement dAs abgestrahlt wird. Hierbei gilt für einen gleichmäßigen Strahlungsfluss:
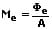
Me: spezifische Ausstrahlung [W/m²]
Φe: Strahlungsfluss [W]
As: Strahlungsfläche [m²]
Variiert der Strahlungsfluss an den Stellen der Strahlungsoberfläche so gilt:
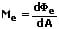
Strahlungsdichte:
Die Strahlungsdichte (Strahldichte) Le definiert die von einer Sendefläche abgegebene Strahlung. Sie ist die Flächendichte der Strahlstärke Ie, bezogen auf die projizierte abstrahlende Fläche. Es gilt:
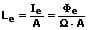
Le: Strahlungsdichte [W/(sr·m²)]
Ie: Strahlstärke [W/sr]
Φe: Strahlungsfluss [W]
As: Abstrahlende Fläche [m²]
Ω: Raumwinkel [sr]
Ist die Strahlungsdichte auf die projizierte abstrahlende Fläche nicht gleichmäßig verteilt, so gilt:
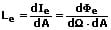
Leuchtdichte:
Die Leuchtdichte Lv beschreibt die Helligkeit ausgedehnter, flächenhafter Lichtquellen und entspricht dem Quotienten aus Lichtstärke und leuchtender Fläche. Es gilt:
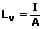
Lv: Leuchtdichte der Lichtquelle [cd/m²]
I. Lichtstärke der leuchtenden Fläche [cd]
A: (scheinbare) Fläche [m²]
Lichtstärke:
Die Lichtstärke beschreibt den auf den Raumwinkel bezogenen Lichtstrom. Sie ist die Eigenschaft einer Lichtquelle und ist unabhängig von der Position des Beobachters. Sie ist als photometrische Basisgröße definiert und als SI-Einheit ist die Candela (cd) festgelegt.
Eine Candela ist die Lichtstärke einer Strahlungsquelle, die monochromatische Strahlung der Frequenz 540·1012 Hertz, (entsprechend einer Vakuumwellenlänge von 555 nm), mit einer Leistung von 1/683 Watt je Steradiant in einer bestimmten Richtung aussendet.
Lichtstrom:
Der Lichtstrom Φ ist eine photometrische Größe für die von einer Lichtquelle je Zeiteinheit abgestrahlte Lichtstärke. Er ist das Produkt der Lichtstärke und dem vom Licht durchstrahlten Raumwinkel. Als SI-Einheit des Lichtstroms ist das Lumen (lm) festgelegt. Ist die Lichtstärke innerhalb des Raumwinkels konstant, so gilt:
Φ = I·Ω
Φ: Lichtstrom [lm]
I: Lichtstärke [cd]
Ω: Raumwinkel [sr]
Ist die Lichtstärke innerhalb des Raumwinkels nicht konstant, dann gilt für den Lichtstrom:
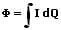
Raumwinkel:
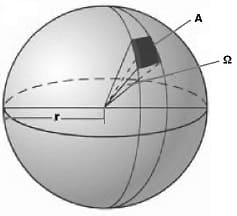
Der Raumwinkel Ω entspricht dem Flächeninhalt A der Teilfläche einer Kugeloberfläche, dividiert durch das Quadrat des Radius r der Kugel.
Ω = A/r²
Ω: Raumwinkel [sr]
A: Teilfläche der Kugeloberfläche [m²]
r: Radius der Kugel [m]
Spezifische Lichtausstrahlung:
Als spezifische Lichtausstrahlung M wird der Lichtstrom bezeichnet, der vom Oberflächenelement einer Lichtquelle ausgeht. Sie ist der Quotient aus Lichtstrom und Oberfläche des Strahlers. Es gilt:
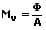
M: spezifische Lichtausstrahlung [lm/m²]
Φ: Lichtstrom [lm]
As: Fläche des Strahlers [m²]
Sind der Lichtstrom und die Oberfläche nicht gleichmäßig verteilt, so gilt:
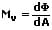
Lichtmenge:
Die Lichtmenge Q gibt die Menge an elektromagnetischer Strahlung an, die für das menschliche Auge zum Sehen nutzbar ist. Sie ist das Produkt des Lichtstroms und der Zeit. Für sie gilt bei konstantem Lichtstrom:
Q = Φ·t
Q: Lichtmenge [lm·s]
Φ: Lichtstrom [lm]
t: Zeit [s]
Ist der Lichtstrom nicht konstant, so gilt:
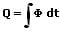
Beleuchtungsstärke:
Mit dem Begriff Beleuchtungsstärke wird der Lichtstrom beschrieben, der auf ein beleuchtetes Objekt (eine Empfängerfläche) trifft. Sie ist der Quotient eines auftreffenden Lichtstroms und der Fläche des Empfängers. Ihre SI-Einheit ist das Lux (lx). 1 Lux = 1 lm/m².
Sie reduziert sich mit dem Quadrat der Entfernung zwischen Lichtquelle und beleuchteter Fläche. Für sie gilt bei konstantem Lichtstrom:
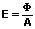
E: Beleuchtungsstärke [lx]
Φ: Lichtstrom [lm]
A: Fläche des Empfängers [m²]
Ist der Lichtstrom nicht konstant, so gilt:
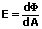
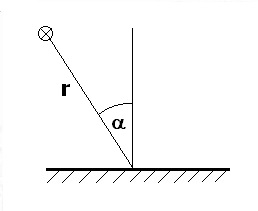
Wird zudem berücksichtigt, dass die Empfängerfläche um den Winkel α gegen die Einstrahlrichtung geneigt sein kann, so ergibt sich:
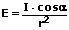
E: Beleuchtungsstärke [lx]
Φ: Lichtsrom [lm]
A: Fläche des Empfängers [m²]
I: Lichtstärke [cd]
r: Abstand der Lichtquelle von Empfängerfläche [m]
α: Winkel zwischen Flächennormale und Strahlungsrichtung
Lambertsches Gesetz:
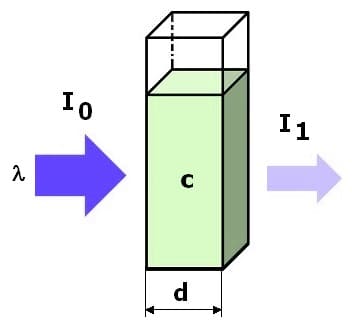
Das Lambertsche Gesetz (Lambert-beersches Gesetz) beschreibt die Extinktion (die Schwächung der Strahlungsintensität des Lichts) mit der Weglänge beim Durchgang durch ein absorbierendes Material und somit den Zusammenhang zwischen der Intensität des transmittierten (ausfallenden Lichts) und der Intensität des einfallenden Lichts einer bestimmten Wellenlänge. Die Extinktion wird durch den Extinktionskoeffizienten, die Stoffmengenkonzentration der Flüssigkeit sowie die Schichtdicke des durchstrahlten Körpers bestimmt. Es gilt:
E = lg(l0/l1) = ε·c·d
E: Extinktion
I0: Intensität des einfallenden Lichts [W/m²]
I1: Intensität des transmittierten Lichts [W/m²]
ε: Absorptionskoeffizient oder Extinktionskoeffizient [m²/mol]
c: Stoffmengenkonzentration der absorbierenden Substanz in Flüssigkeit [mol/m³]
d: Schichtdicke des durchstrahlten Körpers [m]
Belichtung:
Als Belichtung H wird die über eine Zeitspanne Δt empfangene Lichtmenge Q bezogen auf ein Flächenelement A bezeichnet. Bei konstanter Beleuchtungsstärke gilt:
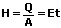
Liegt während der Zeit t keine konstante Beleuchtungsstärke vor, so gilt:
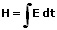
H: Belichtung [lx·s]
Q: Lichtmenge [lm·s]
A: Beleuchtete Fläche [m²]
E: Beleuchtungsstärke [lx]
t: Zeit [s]
Lichtausbeute:
Mit Lichtausbeute ηv einer Lichtquelle (Lampe) wird der Quotient aus dem von der Lampe abgegebenen Lichtstrom Φv und der von ihr aufgenommenen Leistung bezeichnet. Es gilt:
ηv = Φv/P
ηv: Lichtausbeute [lm/W]
Φv: Lichtstrom [lm]
P: Leistungsaufnahme der Lichtquelle [W]
Je höher dieser Wert ist, desto größer ist der für das menschliche Auge nutzbare Lichtstrom bei gegebener Leistungsaufnahme der Lampe.
Solarkonstante:
Von der Sonne wird kontinuierlich eine Leistung von ca. 3,7·1027 W abgestrahlt. Die pro Flächeneinhait auf der Erde auftreffende Leistung wird als Solarkonstante bezeichnet. Ihr Wert beträgt bei vertikal auftreffendem Strahleneinfall ca. 1,37 KW/m².
Solarkonstante = 1,37 KW/m²
In der nachfolgenden Tabelle sind die oben beschriebenen Größen und Einheiten aufgeführt die in der Radiometrie sowie der Photometrie Anwendung finden.
| Größe | Symbol | SI-Einheit |
| Strahlungsfluss | Φe | W |
| Strahlstärke | Ie | W/sr |
| Bestrahlungsstärke | Ee | W/m2 |
| Spezifische Ausstrahlung | Me | W/m2 |
| Strahldichte | Le | W/m2sr |
| Strahlungsenergie | Qe | J |
| Bestrahlung | He | J/m2 |
| Belichtung | H | lx·s |
| Leuchtdichte | Lv | cd/m2 |
| Lichtstärke | Iv | cd = lm/sr |
| Lichtstrom | Φv | lm |
| Spezifische Lichtausstrahlung | Mv | lm/m2 |
| Lichtmenge | Qv | lm·s |
Nachfolgend aufgeführt sind Werte für die Lichtstärke, die Beleuchtungsstärke, die Leuchtdichte sowie für die Lichtausbeute verschiedener Lichtquellen.
Beispiele für Lichtstärken unterschiedlicher Lichtquellen.
| Lichtquelle | Lichtstärke Iv in [cd] |
| Glühwürmchen | 0,0002 |
| Kerze (alle Richtungen) | ca. 1 |
| Glühlampe 100 W (alle Richtungen) | ca. 100 |
| Fahrradlampe 5 Watt | ca. 2,5 |
| Reflektor-Fahrradlampe 5 Watt | ca. 250 |
| Reflektor-Glühlampe 120 Watt | ca. 10000 |
| Leuchtfeuer (Leuchtturm) Helgoland | 40·106 |
| Sonne (alle Richtungen) | 3·1027 |
Beispiele für Beleuchtungsstärken unterschiedlicher Lichtquellen.
| Lichtquelle | Beleuchtungsstärke E in [lx] |
| Sternenlicht | 220·10-9 |
| Nacht bei Vollmond | 0,05 - 0,36 |
| Kerze (bei 1m Entfernung) | 1 |
| Straßenbeleuchtung | 10 |
| Wohnzimmerbeleuchtung | 50 |
| Flurbeleuchtung | 100 |
| Zimmerbeleuchtung | 500 |
| Dämmerung (Sonne knapp unter Horizont) | 750 |
| Innenbeleuchtung Fernsehstudio | 1000 |
| Bedeckter Tag im Winter | 3500 |
| Schattenlicht im Sommer | 10000 |
| Klarer Himmel mit Sonne im Sommer | 130000 |
Beispiele für Leuchtdichten unterschiedlicher Lichtquellen.
| Lichtquelle | Leuchtdichte Lv in [cd/m²] |
| Nachthimmel bewölkt | 10−6 - 10−4 |
| Nachthimmel klar | 0,001 |
| Nachthimmel bei Vollmond | 0,1 |
| LCD-Monitor, schwarz | 0,15 - 0,8 |
| Leuchtstofflampe | 0,2 - 0,4 |
| Röhrenmonitor (weiß) | 80 - 200 |
| Mittlerer bedeckter Himmel | 2000 |
| Mondoberfläche | 2500 |
| Mittlerer klarer Himmel | 8000 |
| 60-W-Glühlampe (matt) | 120000 |
| Xenon-Hochdrucklampe | 50000 - 100000 |
| Natriumdampflampe | 500000 |
| Sonnenscheibe am Horizont | 6·105 |
| Sonnenscheibe am Mittag | 1600·106 |
Beispiele für die Lichtausbeute unterschiedlicher Lampen.
| Lampenart | Lichtausbeute ηv in [lm/W] |
| Glühlampe | 10 - 30 |
| Halogenlampe | 25 |
| Energiesparlampe | 50 - 80 |
| Quecksilberdampflampe | 80 - 105 |
| LED-Lampe | 60 - 150 |
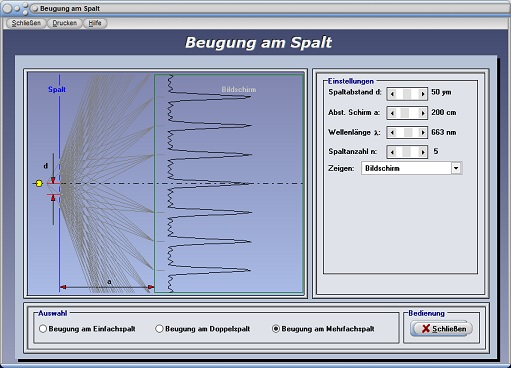
Beugung am Mehrfachspalt - Beugungsmuster 1
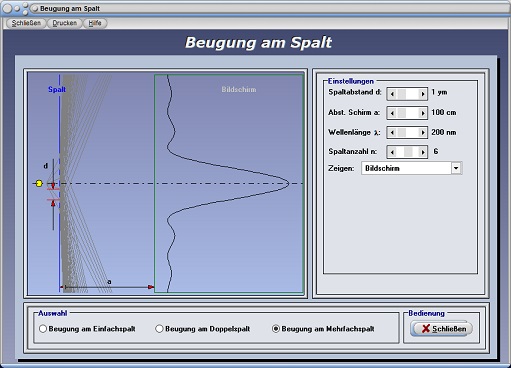
Beugung am Mehrfachspalt - Beugungsmuster 2
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen oder deren Frageworte die Wörter Welche?, Welcher?, Welches? bzw. Wodurch? sind, beantwortet werden und zugrunde liegende Sachverhalte können einfach erklärt werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Doppelspaltexperiment
Wikipedia - Beugung
Wikipedia - Optisches Gitter
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Reflexion - Lichtbrechung - Zerstreuungslinse - Sammellinse - Hohlspiegel - Reflexion am Spiegel - Plancksches Strahlungsgesetz
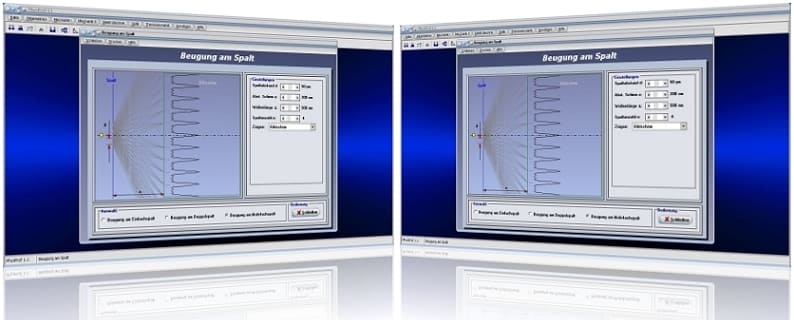
Unterprogramm Beugung am Spalt
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
