MathProf - Primzahl - Primfaktorzerlegung - Primfaktoren - Tabelle

Fachthemen: Primzahlen - Primfaktoren - Primfaktorzerlegung
MathProf - Zahlentheorie - Software für interaktive Mathematik und zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen. Ein Programm zum Einsatz im Mathematikunterricht sowie für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul aus einem Bereich der Zahlentheorie zur Untersuchung natürlicher Zahlen hinsichtlich derer Primzahl-Eigenschaften.
Der in diesem Programmteil implementierte Rechner sucht hierbei unter anderem nach Primzahlen, Primzahlzwillingen, Primzahlvierlingen, Mirp-Primzahlen, Primfaktoren, Cousin-Primzahlen, Fastprime-Primzahlen, Pseudo-Primzahlen sowie Ruth-Aaron-Paaren und gibt diese in einer Liste aus.
Dieses Unterprogramm ermöglicht neben dem Berechnen von Primzahlen unter anderem die Durchführung der Primzahlzerlegung bzw. Primfaktorzerlegung. Auch die Resultate der Eulerschen Phi-Funktion werden berechnet und die Zerlegung von Primzahlen kann veranlasst werden. Die Auflistung ermittelter Ergebnisse erfolgt in einer Tabelle.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind eingebunden.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Primzahlen - Tabelle - Rechner - Primfaktoren - Primzahl - Primfaktor - Beispiele - Berechnen - Berechnung - Zerlegen - Zerlegung - Liste - Übersicht - Finden - Primzahltabelle - Primzahlentabelle - Was ist eine Primzahl - Menge - Primfaktorzerlegung - Primzahlzerlegung - Eulersche Phi Funktion - Primzahlzwilling - Primzahldrilling - Primzahlzwillinge - Primzahldrillinge - Primzahlvierlinge - Pseudoprimzahlen - Finden - Herleitung - Beweis - Primzahlrechner - Primzahlenrechner - 4n+1-Primzahlen - Primzahlpaare - Mirp-Zahlen - Eulersches Theorem - Primzahlen bis 10 - Primzahlen von 1 bis 100 - Primzahlen bis 200 - Primzahlen bis 300 - Primzahlen bis 500 - Primzahlen bis 1000 - Primzahlen bis 10000 - Primzahlen bis 20 - Primzahlen bis 2000 - Primzahlen bis 30 - Primzahlen bis 300 - Primzahlen bis 40 - Primzahlen bis 400 - Primzahlen bis 4000 - Primzahlen bis 30 - Primzahlen bis 50 - Primzahlen bis 5000 - Primzahlen bis 60 - Primzahlen bis 600 - Primzahlen bis 70 - Primzahlen bis 700 - Primzahlen bis 8 - Primzahlen bis 80 - Primzahlen bis 800 - Primzahlen bis 9 - Primzahlen bis 90 - Primzahlen bis 999 - Primzahlen bis 100 - Primzahlen über 100 - Gibt es - Primzahlen ab - Alle Primzahlen - Alle Primzahlen bis 100 - Alle Primzahlen bis 1000 - Alle Primzahlen bis 10000 - Unter - Von - Bis - Über - Erklärung - Einfach erklärt - Wie - Weshalb - Was ist - Warum - Was sind - Welche - Welcher - Welches - Wodurch - Bedeutung - Was bedeutet - Beschreibung - Definition - Differenz - Kleinste Primzahl - Kleiner - Zwischen - Wie viele - Wieviel - Welche - Paare - Sexy-Primzahlen - 6n+1 - Vier Quadrate Satz - Mirp-Primzahlen - ggT - Distanz-m-Primzahlen - Cousin-Primzahlen - Erkennen - Pseudo-Primzahlen - Sophie-Primzahlen - Fastprime Zahlen - Cunningham-Primzahlen - Ruth-Aaron-Paare - Mersenne Zahlen - Mersennesche Zahlen - Mersenne Primzahlen - Zweistellige Primzahl - Fundamentalsatz der Arithmetik - Mathematik - Faktoren - Satz von Fermat - Anzahl - Ermitteln - Große Primzahlen - Primteiler - Sätze von Fermat - Fermatsche Zahlen - Fermat - Satz von Euler - Satz von Euler-Fermat - Kleiner Satz von Fermat - Zahlen - Begriff - Begriffe - Eigenschaften - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Mathe - Lernen - Erlernen - Einführung - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Ermitteln - Übersicht - Tabelle - Programm - Untersuchen - Untersuchung - Faktorisierung - Faktorzerlegung |
Primzahlen - Primfaktoren - Primfaktorzerlegung
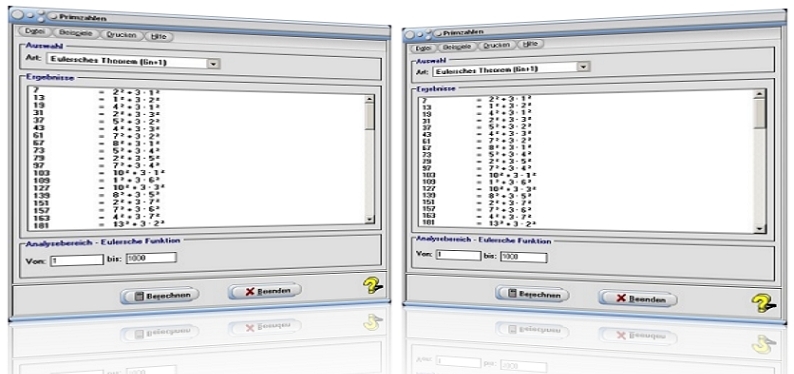
Modul Primzahlen
Das Unterprogramm [Algebra] - [Primzahlen] - Primzahlen ermöglicht die Untersuchung natürlicher Zahlen auf deren
Primzahleigenschaften.

Jede natürliche Zahl, die größer eins ist, kann sofern sie selbst keine Primzahl ist, in Faktoren zerlegt werden, die Primzahlen sind. Mittels einer Primfaktorzerlegung wird eine natürliche Zahl als ein Produkt von Primzahlen beschrieben. Unter einer Primfaktorzerlegung wird das Schreiben einer natürlichen Zahl in Form des Produkts von Primzahlen verstanden. Sie wird auch als Faktorisierung oder Faktorzerlegung bezeichnet.
Primfaktor: Die Primfaktoren (Primteiler) einer Zahl sind Primzahlen, die eine natürliche Zahl teilen. Ist der Teiler einer Zahl eine Primzahl, so wird dieser als Primteiler bezeichnet. Beispielsweise kann die Zahl 104 kann in die Primfaktoren 2 und 13 zerlegt werden und mit dem Produkt der folgenden Primzahlen beschrieben werden: 104 = 2·2·2·13. Bei der Durchführung einer Primzahlzerlegung (dem Erkennen) wird folgender Weg praktiziert:
- Es wird eine Primzahl gesucht, durch welche die zu zerlegende Zahl teilbar ist (begonnen wird stets mit der Zahl 2)
- Die Teilung dieser Zahl mit der ermittelten Primzahl durchgeführt und diese wird notiert
- Die geteilte Zahl wird nach der oben beschriebenen Vorgehensweise so häufig wiederholt durchgeführt bis diese durch keine weitere Primzahl mehr ganzzahlig teilbar ist. Alle hierdurch ermittelten Primzahlen sowie die zuletzt verbleibende Zahl werden ebenfalls notiert.
Beispiel - Primfaktorzerlegung der Zahl 24:
Zunächst wird die Zahl 24 auf deren Teilbarkeit durch 2 getestet.
24 ist durch 2 teilbar und es gilt: 24 = 2 · 12
Nun wird die Zahl 12 auf deren Teilbarkeit durch 2 getestet.
Auch 12 ist durch 2 teilbar und es gilt: 12 = 2 · 6 und somit 24 = 2 · 2 · 6
Darauffolgend wird die Zahl 6 auf Teilbarkeit durch 2 getestet.
Auch 6 ist durch 2 teilbar und es gilt: 6 = 2 · 3 und somit 24 = 2 · 2 · 2 · 3
Da es sich bei der Zahl 3 um eine Primzahl handelt, kann das Verfahren beendet werden.
Zusammengefasst resultiert hieraus: 24 = 2 · 12 = 2 · 2 · 6 = 2 · 2 · 2 · 3
Eine Zahl der Form Fk =
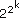 mit einer ganzen Zahl k ∈ IN wird als Fermatsche Zahl bezeichnet. Von Pierre de Fermat (1601-1665) wurde die Vermutung geäußert, dass alle Zahlen dieser Art Primzahlen seien. Dies wurde jeoch bereits 1732 von Leonard Euler widerlegt. Er zeigte, dass bereits die sechste Fermat-Zahl F5 = 4294967297 durch 641 teilbar ist. Die ersten Fermat-Zahlen lauten: F0 = 3 , F1 = 5 , F2 = 17 , F3 = 257, F4 = 65537 und F5 = 4294967297.
mit einer ganzen Zahl k ∈ IN wird als Fermatsche Zahl bezeichnet. Von Pierre de Fermat (1601-1665) wurde die Vermutung geäußert, dass alle Zahlen dieser Art Primzahlen seien. Dies wurde jeoch bereits 1732 von Leonard Euler widerlegt. Er zeigte, dass bereits die sechste Fermat-Zahl F5 = 4294967297 durch 641 teilbar ist. Die ersten Fermat-Zahlen lauten: F0 = 3 , F1 = 5 , F2 = 17 , F3 = 257, F4 = 65537 und F5 = 4294967297. Nachfolgend aufgeführt finden Sie eine Übersicht, der Arten von Primzahlen die sich in diesem Modul ermitteln lassen:
- Primzahlen
- Primzahlzwillinge
- Primzahlvierlinge
- Sexy-Primzahlen
- 4n+1-Primzahlen
- Mirp-Primzahlen
- Eulersches Theorem (6n+1)
- Primfaktoren (Zerlegung einer Zahl in ihre Primfaktoren)
- Distanz-m-Primzahlen
- Cousin-Primzahlen
- Gute Primzahlen
- Fastprime Zahlen
- Eulersche Funktion
- Vierquadrate-Satz nach Lagrange
- Pseudo-Primzahlen
- Sophie-Primzahlen
- Cunningham-Primzahlen
- Ruth-Aaron-Paare
Arten von Primzahlen
Im Weiteren erfolgt die Beschreibung der in diesem Modul berechenbaren Arten von Primzahlen.
1. Primzahlen (Was ist eine Primzahl):

Primzahlen sind natürliche Zahlen, welche genau 2 Teiler besitzen. Sie ergeben bei einer Teilung durch sich selbst die ganze Zahl 1 und sind nur durch die Zahl 1 teilbar. Die kleinste Primzahl ist die Zahl 2, da die Zahl 1 als solche nicht als Primzahl definiert ist.
Der Fundamentalsatz der Arithmetik besagt, dass sich jede ganze Zahl größer als 1 bis zur Ordnung der Faktoren eindeutig als ein Produkt von Primzahlen darstellen lässt, wenn sie selbst keine Primzahl ist.
2. Primzahlzwillinge:

Unter Primzahlzwillingen versteht man Primzahlen, die sich um den Differenzbetrag 2 voneinander unterscheiden. Das kleinste Primzahlpaar ist daher [3;5].
3. Primzahlvierlinge:

Weisen Primzahlen die Abstände 2, 4 und 2 auf, so spricht man von Primzahlvierlingen. Diese treten in einer Dekade auf, bei welcher die auf 1, 3, 7 und 9 endenden Zahlen auch Primzahlen sind (Ausnahme ist der Primzahlvierling 5, 7, 11, 13).
4. Sexy-Primzahlen:

Sexy-Primzahlen werden nach derselben Weise definiert wie Cousin-Primzahlen, jedoch mit dem Unterschied, dass die Differenz zweier Primzahlen den Wert 6 besitzen muss. Werden Primzahlpaare zugelassen, zwischen welchen sich weitere Primzahlen befinden, so ist das kleinste Paar [23;29]. Werden hingegen auch Paare zugelassen, zwischen welchen sich Primzahlen befinden, so bildet das Paar [5;11] das kleinste Sexy-Primzahlpaar. In diesem Unterprogramm werden alle derartigen Primzahlpaare ausgegeben.
5. 4n+1-Primzahlen:

Primzahlen des Typs 4n+1 sind Primzahlen, die u.a. die Eigenschaft besitzen, in die Summe zweier Quadratzahlen zerlegt werden zu können.
6. Mirp-Primzahlen:

Eine Mirp-Zahl ist eine zweistellige Primzahl, welche rückwärts (Ziffernfolge in umgekehrter Reihenfolge) gelesen eine Primzahl darstellt.
7. Eulersches Theorem (6n+1):

Primzahlen des Typs z = 6n+1 können in Zahlen der Form z = a² + 3b² zerlegt werden. Dies besagt das Eulersche Theorem. So kann beispielsweise die Primzahl 7 in die Summe 2² + 3·1², die Primzahl 43 in die Summe 4² + 3·2² gewandelt werden.
8. Distanz-m-Primzahlen:

Unter Distanz-m-Primzahlen werden Primzahlpaare verstanden, zwischen welchen sich keine weiteren Primzahlen befinden und die Differenz zwischen diesen der Zahl m entspricht (siehe auch Primzahlzwillinge, Cousin-Primzahlen, Sexy-Primzahlen). Bei einer geforderten Distanz von 6 sind die ersten Paare, die diese Bedingung erfüllen somit [5,11], [7,13], [11,17] usw. Derartige Primzahlpaare werden ab der Zahl 3 ermittelt. Mit der kleinsten Primzahl 2 wird diese Untersuchung nicht durchgeführt.
9. Cousin-Primzahlen:

Ein Primzahlpaar dessen Differenz exakt 4 ist, wird Cousin-Primzahlpaar genannt. Die einzige Ausnahme bildet das Paar [3;7]. Dieses besitzt zwar die Differenz 4, da aber die Primzahl 5 dazwischen liegt, wird dieses Paar nicht als Cousin-Primzahlpaar gewertet.
10. Gute Primzahlen:

Gute Primzahlen sind Primzahlen deren Quadrat größer ist als das Produkt der vorigen oder nachfolgenden Primzahl.
11. Fastprime Zahlen:

Fastprime Zahlen werden nach deren Grad eingeteilt. Die Anzahl der Faktoren, in die sich eine natürliche Zahl bei derer Primfaktorzerlegung zerlegen lässt, gibt diesen an.
12. Eulersche Funktion:

Die Eulersche Phi-Funktion ist eine zahlentheoretische Funktion. Sie ordnet jeder natürlichen n die Anzahl a der natürlichen Zahlen von 1 bis n zu, die zu n teilerfremd sind (also ggT(a,n) = 1).
Sie ist benannt nach Leonhard Euler und wird mit dem griechischen Buchstaben φ bezeichnet.
13. Vierquadrate-Satz nach Lagrange:

Der Vierquadrate-Satz nach Lagrange besagt:
Jede natürliche Zahl kann als Summe von vier Quadratzahlen geschrieben werden. Demzufolge sind Primzahlen der Form 4n+3 als Summe vierer Quadrate darstellbar.
14. Pseudo-Primzahlen:

Kleiner Satz von Fermat:
Der kleine Satz von Fermat lautet: Für alle Primzahlen p und alle natürlichen Zahlen n, die kein Vielfaches von p sind, gilt: n(p - 1) ≡ 1 mod (p) (np-1 ergibt bei der Division durch p stets den Rest 1).
Existieren natürliche Zahlen, die keine Primzahlen sind, jedoch obige Bedingung trotzdem erfüllen, so nennt man diese Pseudoprimzahlen (zur Basis n). Für sie muss gelten: n(p - 1) ≡ 1 mod (p), wenn 2 ≤ n ≤ p-2 und ggT(n,p) = 1.
Der Satz von Fermat ist ein Sonderfall des Satzes von Euler, welcher lediglich Gültigkeit für einen Primzahlmodul besitzt.
Satz von Euler:
Der Satz von Euler (Satz von Euler-Fermat) lautet: Sei m ≥ 1, und sei a teilerfremd zu m. Dann gilt aφ(m) ≡ 1 mod (m).
Er ist nach Leonhard Euler und Pierre de Fermat benannt und stellt eine Verallgemeinerung des kleinen fermatschen Satzes auf beliebige Moduli n ∈ N dar.
15. Sophie-Primzahlen:

Eine Sophie-Primzahl ist eine Primzahl p, für welche eine Primzahl 2p+1 gleichermaßen eine Primzahl ist.
16. Cunningham-Primzahlen:

Cunningham-Primzahlen 1. Art sind Folgen von Primzahlen der Form: p, 2p+1, 2(2p+1)+1, 2(2(2p+1)+1)+1, ....
Cunningham-Primzahlen 2. Art sind Folgen von Primzahlen der Form: p, 2p+1, 4p+3, 8p+, ...
17. Ruth-Aaron-Paare:

Als Ruth-Aaron-Zahlen bezeichnet man ein Paar aufeinanderfolgender natürlicher Zahlen, deren Primfaktoren die gleiche Summe haben.
Liste aller Primzahlen zwischen 1 und 10000 - Primzahlentabelle
Primzahltabelle (Primzahlentabelle): Nachfolgend finden Sie eine Liste aller Primzahlen zwischen der Zahl 1 und der Zahl 10000:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733, 3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911, 3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001, 4003, 4007, 4013, 4019, 4021, 4027, 4049, 4051, 4057, 4073, 4079, 4091, 4093, 4099, 4111, 4127, 4129, 4133, 4139, 4153, 4157, 4159, 4177, 4201, 4211, 4217, 4219, 4229, 4231, 4241, 4243, 4253, 4259, 4261, 4271, 4273, 4283, 4289, 4297, 4327, 4337, 4339, 4349, 4357, 4363, 4373, 4391, 4397, 4409, 4421, 4423, 4441, 4447, 4451, 4457, 4463, 4481, 4483, 4493, 4507, 4513, 4517, 4519, 4523, 4547, 4549, 4561, 4567, 4583, 4591, 4597, 4603, 4621, 4637, 4639, 4643, 4649, 4651, 4657, 4663, 4673, 4679, 4691, 4703, 4721, 4723, 4729, 4733, 4751, 4759, 4783, 4787, 4789, 4793, 4799, 4801, 4813, 4817, 4831, 4861, 4871, 4877, 4889, 4903, 4909, 4919, 4931, 4933, 4937, 4943, 4951, 4957, 4967, 4969, 4973, 4987, 4993, 4999, 5003, 5009, 5011, 5021, 5023, 5039, 5051, 5059, 5077, 5081, 5087, 5099, 5101, 5107, 5113, 5119, 5147, 5153, 5167, 5171, 5179, 5189, 5197, 5209, 5227, 5231, 5233, 5237, 5261, 5273, 5279, 5281, 5297, 5303, 5309, 5323, 5333, 5347, 5351, 5381, 5387, 5393, 5399, 5407, 5413, 5417, 5419, 5431, 5437, 5441, 5443, 5449, 5471, 5477, 5479, 5483, 5501, 5503, 5507, 5519, 5521, 5527, 5531, 5557, 5563, 5569, 5573, 5581, 5591, 5623, 5639, 5641, 5647, 5651, 5653, 5657, 5659, 5669, 5683, 5689, 5693, 5701, 5711, 5717, 5737, 5741, 5743, 5749, 5779, 5783, 5791, 5801, 5807, 5813, 5821, 5827, 5839, 5843, 5849, 5851, 5857, 5861, 5867, 5869, 5879, 5881, 5897, 5903, 5923, 5927, 5939, 5953, 5981, 5987, 6007, 6011, 6029, 6037, 6043, 6047, 6053, 6067, 6073, 6079, 6089, 6091, 6101, 6113, 6121, 6131, 6133, 6143, 6151, 6163, 6173, 6197, 6199, 6203, 6211, 6217, 6221, 6229, 6247, 6257, 6263, 6269, 6271, 6277, 6287, 6299, 6301, 6311, 6317, 6323, 6329, 6337, 6343, 6353, 6359, 6361, 6367, 6373, 6379, 6389, 6397, 6421, 6427, 6449, 6451, 6469, 6473, 6481, 6491, 6521, 6529, 6547, 6551, 6553, 6563, 6569, 6571, 6577, 6581, 6599, 6607, 6619, 6637, 6653, 6659, 6661, 6673, 6679, 6689, 6691, 6701, 6703, 6709, 6719, 6733, 6737, 6761, 6763, 6779, 6781, 6791, 6793, 6803, 6823, 6827, 6829, 6833, 6841, 6857, 6863, 6869, 6871, 6883, 6899, 6907, 6911, 6917, 6947, 6949, 6959, 6961, 6967, 6971, 6977, 6983, 6991, 6997, 7001, 7013, 7019, 7027, 7039, 7043, 7057, 7069, 7079, 7103, 7109, 7121, 7127, 7129, 7151, 7159, 7177, 7187, 7193, 7207, 7211, 7213, 7219, 7229, 7237, 7243, 7247, 7253, 7283, 7297, 7307, 7309, 7321, 7331, 7333, 7349, 7351, 7369, 7393, 7411, 7417, 7433, 7451, 7457, 7459, 7477, 7481, 7487, 7489, 7499, 7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561, 7573, 7577, 7583, 7589, 7591, 7603, 7607, 7621, 7639, 7643, 7649, 7669, 7673, 7681, 7687, 7691, 7699, 7703, 7717, 7723, 7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823, 7829, 7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919, 7927, 7933, 7937, 7949, 7951, 7963, 7993, 8009, 8011, 8017, 8039, 8053, 8059, 8069, 8081, 8087, 8089, 8093, 8101, 8111, 8117, 8123, 8147, 8161, 8167, 8171, 8179, 8191, 8209, 8219, 8221, 8231, 8233, 8237, 8243, 8263, 8269, 8273, 8287, 8291, 8293, 8297, 8311, 8317, 8329, 8353, 8363, 8369, 8377, 8387, 8389, 8419, 8423, 8429, 8431, 8443, 8447, 8461, 8467, 8501, 8513, 8521, 8527, 8537, 8539, 8543, 8563, 8573, 8581, 8597, 8599, 8609, 8623, 8627, 8629, 8641, 8647, 8663, 8669, 8677, 8681, 8689, 8693, 8699, 8707, 8713, 8719, 8731, 8737, 8741, 8747, 8753, 8761, 8779, 8783, 8803, 8807, 8819, 8821, 8831, 8837, 8839, 8849, 8861, 8863, 8867, 8887, 8893, 8923, 8929, 8933, 8941, 8951, 8963, 8969, 8971, 8999, 9001, 9007, 9011, 9013, 9029, 9041, 9043, 9049, 9059, 9067, 9091, 9103, 9109, 9127, 9133, 9137, 9151, 9157, 9161, 9173, 9181, 9187, 9199, 9203, 9209, 9221, 9227, 9239, 9241, 9257, 9277, 9281, 9283, 9293, 9311, 9319, 9323, 9337, 9341, 9343, 9349, 9371, 9377, 9391, 9397, 9403, 9413, 9419, 9421, 9431, 9433, 9437, 9439, 9461, 9463, 9467, 9473, 9479, 9491, 9497, 9511, 9521, 9533, 9539, 9547, 9551, 9587, 9601, 9613, 9619, 9623, 9629, 9631, 9643, 9649, 9661, 9677, 9679, 9689, 9697, 9719, 9721, 9733, 9739, 9743, 9749, 9767, 9769, 9781, 9787, 9791, 9803, 9811, 9817, 9829, 9833, 9839, 9851, 9857, 9859, 9871, 9883, 9887, 9901, 9907, 9923, 9929, 9931, 9941, 9949, 9967, 9973
In der nachfolgend gezeigten Tabelle aufgeführt sind die Primzahlfaktoren der Zahlen des Bereichs von 1 bis 1500.
| Zahl | Primzahlfaktoren |
| 1 | --------- |
| 2 | Primzahl |
| 3 | Primzahl |
| 4 | 2*2 |
| 5 | Primzahl |
| 6 | 2*3 |
| 7 | Primzahl |
| 8 | 2*2*2 |
| 9 | 3*3 |
| 10 | 2*5 |
| 11 | Primzahl |
| 12 | 2*2*3 |
| 13 | Primzahl |
| 14 | 2*7 |
| 15 | 3*5 |
| 16 | 2*2*2*2 |
| 17 | Primzahl |
| 18 | 2*3*3 |
| 19 | Primzahl |
| 20 | 2*2*5 |
| 21 | 3*7 |
| 22 | 2*11 |
| 23 | Primzahl |
| 24 | 2*2*2*3 |
| 25 | 5*5 |
| 26 | 2*13 |
| 27 | 3*3*3 |
| 28 | 2*2*7 |
| 29 | Primzahl |
| 30 | 2*3*5 |
| 31 | Primzahl |
| 32 | 2*2*2*2*2 |
| 33 | 3*11 |
| 34 | 2*17 |
| 35 | 5*7 |
| 36 | 2*2*3*3 |
| 37 | Primzahl |
| 38 | 2*19 |
| 39 | 3*13 |
| 40 | 2*2*2*5 |
| 41 | Primzahl |
| 42 | 2*3*7 |
| 43 | Primzahl |
| 44 | 2*2*11 |
| 45 | 3*3*5 |
| 46 | 2*23 |
| 47 | Primzahl |
| 48 | 2*2*2*2*3 |
| 49 | 7*7 |
| 50 | 2*5*5 |
| 51 | 3*17 |
| 52 | 2*2*13 |
| 53 | Primzahl |
| 54 | 2*3*3*3 |
| 55 | 5*11 |
| 56 | 2*2*2*7 |
| 57 | 3*19 |
| 58 | 2*29 |
| 59 | Primzahl |
| 60 | 2*2*3*5 |
| 61 | Primzahl |
| 62 | 2*31 |
| 63 | 3*3*7 |
| 64 | 2*2*2*2*2*2 |
| 65 | 5*13 |
| 66 | 2*3*11 |
| 67 | Primzahl |
| 68 | 2*2*17 |
| 69 | 3*23 |
| 70 | 2*5*7 |
| 71 | Primzahl |
| 72 | 2*2*2*3*3 |
| 73 | Primzahl |
| 74 | 2*37 |
| 75 | 3*5*5 |
| 76 | 2*2*19 |
| 77 | 7*11 |
| 78 | 2*3*13 |
| 79 | Primzahl |
| 80 | 2*2*2*2*5 |
| 81 | 3*3*3*3 |
| 82 | 2*41 |
| 83 | Primzahl |
| 84 | 2*2*3*7 |
| 85 | 5*17 |
| 86 | 2*43 |
| 87 | 3*29 |
| 88 | 2*2*2*11 |
| 89 | Primzahl |
| 90 | 2*3*3*5 |
| 91 | 7*13 |
| 92 | 2*2*23 |
| 93 | 3*31 |
| 94 | 2*47 |
| 95 | 5*19 |
| 96 | 2*2*2*2*2*3 |
| 97 | Primzahl |
| 98 | 2*7*7 |
| 99 | 3*3*11 |
| 100 | 2*2*5*5 |
| 101 | Primzahl |
| 102 | 2*3*17 |
| 103 | Primzahl |
| 104 | 2*2*2*13 |
| 105 | 3*5*7 |
| 106 | 2*53 |
| 107 | Primzahl |
| 108 | 2*2*3*3*3 |
| 109 | Primzahl |
| 110 | 2*5*11 |
| 111 | 3*37 |
| 112 | 2*2*2*2*7 |
| 113 | Primzahl |
| 114 | 2*3*19 |
| 115 | 5*23 |
| 116 | 2*2*29 |
| 117 | 3*3*13 |
| 118 | 2*59 |
| 119 | 7*17 |
| 120 | 2*2*2*3*5 |
| 121 | 11*11 |
| 122 | 2*61 |
| 123 | 3*41 |
| 124 | 2*2*31 |
| 125 | 5*5*5 |
| 126 | 2*3*3*7 |
| 127 | Primzahl |
| 128 | 2*2*2*2*2*2*2 |
| 129 | 3*43 |
| 130 | 2*5*13 |
| 131 | Primzahl |
| 132 | 2*2*3*11 |
| 133 | 7*19 |
| 134 | 2*67 |
| 135 | 3*3*3*5 |
| 136 | 2*2*2*17 |
| 137 | Primzahl |
| 138 | 2*3*23 |
| 139 | Primzahl |
| 140 | 2*2*5*7 |
| 141 | 3*47 |
| 142 | 2*71 |
| 143 | 11*13 |
| 144 | 2*2*2*2*3*3 |
| 145 | 5*29 |
| 146 | 2*73 |
| 147 | 3*7*7 |
| 148 | 2*2*37 |
| 149 | Primzahl |
| 150 | 2*3*5*5 |
| 151 | Primzahl |
| 152 | 2*2*2*19 |
| 153 | 3*3*17 |
| 154 | 2*7*11 |
| 155 | 5*31 |
| 156 | 2*2*3*13 |
| 157 | Primzahl |
| 158 | 2*79 |
| 159 | 3*53 |
| 160 | 2*2*2*2*2*5 |
| 161 | 7*23 |
| 162 | 2*3*3*3*3 |
| 163 | Primzahl |
| 164 | 2*2*41 |
| 165 | 3*5*11 |
| 166 | 2*83 |
| 167 | Primzahl |
| 168 | 2*2*2*3*7 |
| 169 | 13*13 |
| 170 | 2*5*17 |
| 171 | 3*3*19 |
| 172 | 2*2*43 |
| 173 | Primzahl |
| 174 | 2*3*29 |
| 175 | 5*5*7 |
| 176 | 2*2*2*2*11 |
| 177 | 3*59 |
| 178 | 2*89 |
| 179 | Primzahl |
| 180 | 2*2*3*3*5 |
| 181 | Primzahl |
| 182 | 2*7*13 |
| 183 | 3*61 |
| 184 | 2*2*2*23 |
| 185 | 5*37 |
| 186 | 2*3*31 |
| 187 | 11*17 |
| 188 | 2*2*47 |
| 189 | 3*3*3*7 |
| 190 | 2*5*19 |
| 191 | Primzahl |
| 192 | 2*2*2*2*2*2*3 |
| 193 | Primzahl |
| 194 | 2*97 |
| 195 | 3*5*13 |
| 196 | 2*2*7*7 |
| 197 | Primzahl |
| 198 | 2*3*3*11 |
| 199 | Primzahl |
| 200 | 2*2*2*5*5 |
| 201 | 3*67 |
| 202 | 2*101 |
| 203 | 7*29 |
| 204 | 2*2*3*17 |
| 205 | 5*41 |
| 206 | 2*103 |
| 207 | 3*3*23 |
| 208 | 2*2*2*2*13 |
| 209 | 11*19 |
| 210 | 2*3*5*7 |
| 211 | Primzahl |
| 212 | 2*2*53 |
| 213 | 3*71 |
| 214 | 2*107 |
| 215 | 5*43 |
| 216 | 2*2*2*3*3*3 |
| 217 | 7*31 |
| 218 | 2*109 |
| 219 | 3*73 |
| 220 | 2*2*5*11 |
| 221 | 13*17 |
| 222 | 2*3*37 |
| 223 | Primzahl |
| 224 | 2*2*2*2*2*7 |
| 225 | 3*3*5*5 |
| 226 | 2*113 |
| 227 | Primzahl |
| 228 | 2*2*3*19 |
| 229 | Primzahl |
| 230 | 2*5*23 |
| 231 | 3*7*11 |
| 232 | 2*2*2*29 |
| 233 | Primzahl |
| 234 | 2*3*3*13 |
| 235 | 5*47 |
| 236 | 2*2*59 |
| 237 | 3*79 |
| 238 | 2*7*17 |
| 239 | Primzahl |
| 240 | 2*2*2*2*3*5 |
| 241 | Primzahl |
| 242 | 2*11*11 |
| 243 | 3*3*3*3*3 |
| 244 | 2*2*61 |
| 245 | 5*7*7 |
| 246 | 2*3*41 |
| 247 | 13*19 |
| 248 | 2*2*2*31 |
| 249 | 3*83 |
| 250 | 2*5*5*5 |
| 251 | Primzahl |
| 252 | 2*2*3*3*7 |
| 253 | 11*23 |
| 254 | 2*127 |
| 255 | 3*5*17 |
| 256 | 2*2*2*2*2*2*2*2 |
| 257 | Primzahl |
| 258 | 2*3*43 |
| 259 | 7*37 |
| 260 | 2*2*5*13 |
| 261 | 3*3*29 |
| 262 | 2*131 |
| 263 | Primzahl |
| 264 | 2*2*2*3*11 |
| 265 | 5*53 |
| 266 | 2*7*19 |
| 267 | 3*89 |
| 268 | 2*2*67 |
| 269 | Primzahl |
| 270 | 2*3*3*3*5 |
| 271 | Primzahl |
| 272 | 2*2*2*2*17 |
| 273 | 3*7*13 |
| 274 | 2*137 |
| 275 | 5*5*11 |
| 276 | 2*2*3*23 |
| 277 | Primzahl |
| 278 | 2*139 |
| 279 | 3*3*31 |
| 280 | 2*2*2*5*7 |
| 281 | Primzahl |
| 282 | 2*3*47 |
| 283 | Primzahl |
| 284 | 2*2*71 |
| 285 | 3*5*19 |
| 286 | 2*11*13 |
| 287 | 7*41 |
| 288 | 2*2*2*2*2*3*3 |
| 289 | 17*17 |
| 290 | 2*5*29 |
| 291 | 3*97 |
| 292 | 2*2*73 |
| 293 | Primzahl |
| 294 | 2*3*7*7 |
| 295 | 5*59 |
| 296 | 2*2*2*37 |
| 297 | 3*3*3*11 |
| 298 | 2*149 |
| 299 | 13*23 |
| 300 | 2*2*3*5*5 |
| 301 | 7*43 |
| 302 | 2*151 |
| 303 | 3*101 |
| 304 | 2*2*2*2*19 |
| 305 | 5*61 |
| 306 | 2*3*3*17 |
| 307 | Primzahl |
| 308 | 2*2*7*11 |
| 309 | 3*103 |
| 310 | 2*5*31 |
| 311 | Primzahl |
| 312 | 2*2*2*3*13 |
| 313 | Primzahl |
| 314 | 2*157 |
| 315 | 3*3*5*7 |
| 316 | 2*2*79 |
| 317 | Primzahl |
| 318 | 2*3*53 |
| 319 | 11*29 |
| 320 | 2*2*2*2*2*2*5 |
| 321 | 3*107 |
| 322 | 2*7*23 |
| 323 | 17*19 |
| 324 | 2*2*3*3*3*3 |
| 325 | 5*5*13 |
| 326 | 2*163 |
| 327 | 3*109 |
| 328 | 2*2*2*41 |
| 329 | 7*47 |
| 330 | 2*3*5*11 |
| 331 | Primzahl |
| 332 | 2*2*83 |
| 333 | 3*3*37 |
| 334 | 2*167 |
| 335 | 5*67 |
| 336 | 2*2*2*2*3*7 |
| 337 | Primzahl |
| 338 | 2*13*13 |
| 339 | 3*113 |
| 340 | 2*2*5*17 |
| 341 | 11*31 |
| 342 | 2*3*3*19 |
| 343 | 7*7*7 |
| 344 | 2*2*2*43 |
| 345 | 3*5*23 |
| 346 | 2*173 |
| 347 | Primzahl |
| 348 | 2*2*3*29 |
| 349 | Primzahl |
| 350 | 2*5*5*7 |
| 351 | 3*3*3*13 |
| 352 | 2*2*2*2*2*11 |
| 353 | Primzahl |
| 354 | 2*3*59 |
| 355 | 5*71 |
| 356 | 2*2*89 |
| 357 | 3*7*17 |
| 358 | 2*179 |
| 359 | Primzahl |
| 360 | 2*2*2*3*3*5 |
| 361 | 19*19 |
| 362 | 2*181 |
| 363 | 3*11*11 |
| 364 | 2*2*7*13 |
| 365 | 5*73 |
| 366 | 2*3*61 |
| 367 | Primzahl |
| 368 | 2*2*2*2*23 |
| 369 | 3*3*41 |
| 370 | 2*5*37 |
| 371 | 7*53 |
| 372 | 2*2*3*31 |
| 373 | Primzahl |
| 374 | 2*11*17 |
| 375 | 3*5*5*5 |
| 376 | 2*2*2*47 |
| 377 | 13*29 |
| 378 | 2*3*3*3*7 |
| 379 | Primzahl |
| 380 | 2*2*5*19 |
| 381 | 3*127 |
| 382 | 2*191 |
| 383 | Primzahl |
| 384 | 2*2*2*2*2*2*2*3 |
| 385 | 5*7*11 |
| 386 | 2*193 |
| 387 | 3*3*43 |
| 388 | 2*2*97 |
| 389 | Primzahl |
| 390 | 2*3*5*13 |
| 391 | 17*23 |
| 392 | 2*2*2*7*7 |
| 393 | 3*131 |
| 394 | 2*197 |
| 395 | 5*79 |
| 396 | 2*2*3*3*11 |
| 397 | Primzahl |
| 398 | 2*199 |
| 399 | 3*7*19 |
| 400 | 2*2*2*2*5*5 |
| 401 | Primzahl |
| 402 | 2*3*67 |
| 403 | 13*31 |
| 404 | 2*2*101 |
| 405 | 3*3*3*3*5 |
| 406 | 2*7*29 |
| 407 | 11*37 |
| 408 | 2*2*2*3*17 |
| 409 | Primzahl |
| 410 | 2*5*41 |
| 411 | 3*137 |
| 412 | 2*2*103 |
| 413 | 7*59 |
| 414 | 2*3*3*23 |
| 415 | 5*83 |
| 416 | 2*2*2*2*2*13 |
| 417 | 3*139 |
| 418 | 2*11*19 |
| 419 | Primzahl |
| 420 | 2*2*3*5*7 |
| 421 | Primzahl |
| 422 | 2*211 |
| 423 | 3*3*47 |
| 424 | 2*2*2*53 |
| 425 | 5*5*17 |
| 426 | 2*3*71 |
| 427 | 7*61 |
| 428 | 2*2*107 |
| 429 | 3*11*13 |
| 430 | 2*5*43 |
| 431 | Primzahl |
| 432 | 2*2*2*2*3*3*3 |
| 433 | Primzahl |
| 434 | 2*7*31 |
| 435 | 3*5*29 |
| 436 | 2*2*109 |
| 437 | 19*23 |
| 438 | 2*3*73 |
| 439 | Primzahl |
| 440 | 2*2*2*5*11 |
| 441 | 3*3*7*7 |
| 442 | 2*13*17 |
| 443 | Primzahl |
| 444 | 2*2*3*37 |
| 445 | 5*89 |
| 446 | 2*223 |
| 447 | 3*149 |
| 448 | 2*2*2*2*2*2*7 |
| 449 | Primzahl |
| 450 | 2*3*3*5*5 |
| 451 | 11*41 |
| 452 | 2*2*113 |
| 453 | 3*151 |
| 454 | 2*227 |
| 455 | 5*7*13 |
| 456 | 2*2*2*3*19 |
| 457 | Primzahl |
| 458 | 2*229 |
| 459 | 3*3*3*17 |
| 460 | 2*2*5*23 |
| 461 | Primzahl |
| 462 | 2*3*7*11 |
| 463 | Primzahl |
| 464 | 2*2*2*2*29 |
| 465 | 3*5*31 |
| 466 | 2*233 |
| 467 | Primzahl |
| 468 | 2*2*3*3*13 |
| 469 | 7*67 |
| 470 | 2*5*47 |
| 471 | 3*157 |
| 472 | 2*2*2*59 |
| 473 | 11*43 |
| 474 | 2*3*79 |
| 475 | 5*5*19 |
| 476 | 2*2*7*17 |
| 477 | 3*3*53 |
| 478 | 2*239 |
| 479 | Primzahl |
| 480 | 2*2*2*2*2*3*5 |
| 481 | 13*37 |
| 482 | 2*241 |
| 483 | 3*7*23 |
| 484 | 2*2*11*11 |
| 485 | 5*97 |
| 486 | 2*3*3*3*3*3 |
| 487 | Primzahl |
| 488 | 2*2*2*61 |
| 489 | 3*163 |
| 490 | 2*5*7*7 |
| 491 | Primzahl |
| 492 | 2*2*3*41 |
| 493 | 17*29 |
| 494 | 2*13*19 |
| 495 | 3*3*5*11 |
| 496 | 2*2*2*2*31 |
| 497 | 7*71 |
| 498 | 2*3*83 |
| 499 | Primzahl |
| 500 | 2*2*5*5*5 |
| 501 | 3*167 |
| 502 | 2*251 |
| 503 | Primzahl |
| 504 | 2*2*2*3*3*7 |
| 505 | 5*101 |
| 506 | 2*11*23 |
| 507 | 3*13*13 |
| 508 | 2*2*127 |
| 509 | Primzahl |
| 510 | 2*3*5*17 |
| 511 | 7*73 |
| 512 | 2*2*2*2*2*2*2*2*2 |
| 513 | 3*3*3*19 |
| 514 | 2*257 |
| 515 | 5*103 |
| 516 | 2*2*3*43 |
| 517 | 11*47 |
| 518 | 2*7*37 |
| 519 | 3*173 |
| 520 | 2*2*2*5*13 |
| 521 | Primzahl |
| 522 | 2*3*3*29 |
| 523 | Primzahl |
| 524 | 2*2*131 |
| 525 | 3*5*5*7 |
| 526 | 2*263 |
| 527 | 17*31 |
| 528 | 2*2*2*2*3*11 |
| 529 | 23*23 |
| 530 | 2*5*53 |
| 531 | 3*3*59 |
| 532 | 2*2*7*19 |
| 533 | 13*41 |
| 534 | 2*3*89 |
| 535 | 5*107 |
| 536 | 2*2*2*67 |
| 537 | 3*179 |
| 538 | 2*269 |
| 539 | 7*7*11 |
| 540 | 2*2*3*3*3*5 |
| 541 | Primzahl |
| 542 | 2*271 |
| 543 | 3*181 |
| 544 | 2*2*2*2*2*17 |
| 545 | 5*109 |
| 546 | 2*3*7*13 |
| 547 | Primzahl |
| 548 | 2*2*137 |
| 549 | 3*3*61 |
| 550 | 2*5*5*11 |
| 551 | 19*29 |
| 552 | 2*2*2*3*23 |
| 553 | 7*79 |
| 554 | 2*277 |
| 555 | 3*5*37 |
| 556 | 2*2*139 |
| 557 | Primzahl |
| 558 | 2*3*3*31 |
| 559 | 13*43 |
| 560 | 2*2*2*2*5*7 |
| 561 | 3*11*17 |
| 562 | 2*281 |
| 563 | Primzahl |
| 564 | 2*2*3*47 |
| 565 | 5*113 |
| 566 | 2*283 |
| 567 | 3*3*3*3*7 |
| 568 | 2*2*2*71 |
| 569 | Primzahl |
| 570 | 2*3*5*19 |
| 571 | Primzahl |
| 572 | 2*2*11*13 |
| 573 | 3*191 |
| 574 | 2*7*41 |
| 575 | 5*5*23 |
| 576 | 2*2*2*2*2*2*3*3 |
| 577 | Primzahl |
| 578 | 2*17*17 |
| 579 | 3*193 |
| 580 | 2*2*5*29 |
| 581 | 7*83 |
| 582 | 2*3*97 |
| 583 | 11*53 |
| 584 | 2*2*2*73 |
| 585 | 3*3*5*13 |
| 586 | 2*293 |
| 587 | Primzahl |
| 588 | 2*2*3*7*7 |
| 589 | 19*31 |
| 590 | 2*5*59 |
| 591 | 3*197 |
| 592 | 2*2*2*2*37 |
| 593 | Primzahl |
| 594 | 2*3*3*3*11 |
| 595 | 5*7*17 |
| 596 | 2*2*149 |
| 597 | 3*199 |
| 598 | 2*13*23 |
| 599 | Primzahl |
| 600 | 2*2*2*3*5*5 |
| 601 | Primzahl |
| 602 | 2*7*43 |
| 603 | 3*3*67 |
| 604 | 2*2*151 |
| 605 | 5*11*11 |
| 606 | 2*3*101 |
| 607 | Primzahl |
| 608 | 2*2*2*2*2*19 |
| 609 | 3*7*29 |
| 610 | 2*5*61 |
| 611 | 13*47 |
| 612 | 2*2*3*3*17 |
| 613 | Primzahl |
| 614 | 2*307 |
| 615 | 3*5*41 |
| 616 | 2*2*2*7*11 |
| 617 | Primzahl |
| 618 | 2*3*103 |
| 619 | Primzahl |
| 620 | 2*2*5*31 |
| 621 | 3*3*3*23 |
| 622 | 2*311 |
| 623 | 7*89 |
| 624 | 2*2*2*2*3*13 |
| 625 | 5*5*5*5 |
| 626 | 2*313 |
| 627 | 3*11*19 |
| 628 | 2*2*157 |
| 629 | 17*37 |
| 630 | 2*3*3*5*7 |
| 631 | Primzahl |
| 632 | 2*2*2*79 |
| 633 | 3*211 |
| 634 | 2*317 |
| 635 | 5*127 |
| 636 | 2*2*3*53 |
| 637 | 7*7*13 |
| 638 | 2*11*29 |
| 639 | 3*3*71 |
| 640 | 2*2*2*2*2*2*2*5 |
| 641 | Primzahl |
| 642 | 2*3*107 |
| 643 | Primzahl |
| 644 | 2*2*7*23 |
| 645 | 3*5*43 |
| 646 | 2*17*19 |
| 647 | Primzahl |
| 648 | 2*2*2*3*3*3*3 |
| 649 | 11*59 |
| 650 | 2*5*5*13 |
| 651 | 3*7*31 |
| 652 | 2*2*163 |
| 653 | Primzahl |
| 654 | 2*3*109 |
| 655 | 5*131 |
| 656 | 2*2*2*2*41 |
| 657 | 3*3*73 |
| 658 | 2*7*47 |
| 659 | Primzahl |
| 660 | 2*2*3*5*11 |
| 661 | Primzahl |
| 662 | 2*331 |
| 663 | 3*13*17 |
| 664 | 2*2*2*83 |
| 665 | 5*7*19 |
| 666 | 2*3*3*37 |
| 667 | 23*29 |
| 668 | 2*2*167 |
| 669 | 3*223 |
| 670 | 2*5*67 |
| 671 | 11*61 |
| 672 | 2*2*2*2*2*3*7 |
| 673 | Primzahl |
| 674 | 2*337 |
| 675 | 3*3*3*5*5 |
| 676 | 2*2*13*13 |
| 677 | Primzahl |
| 678 | 2*3*113 |
| 679 | 7*97 |
| 680 | 2*2*2*5*17 |
| 681 | 3*227 |
| 682 | 2*11*31 |
| 683 | Primzahl |
| 684 | 2*2*3*3*19 |
| 685 | 5*137 |
| 686 | 2*7*7*7 |
| 687 | 3*229 |
| 688 | 2*2*2*2*43 |
| 689 | 13*53 |
| 690 | 2*3*5*23 |
| 691 | Primzahl |
| 692 | 2*2*173 |
| 693 | 3*3*7*11 |
| 694 | 2*347 |
| 695 | 5*139 |
| 696 | 2*2*2*3*29 |
| 697 | 17*41 |
| 698 | 2*349 |
| 699 | 3*233 |
| 700 | 2*2*5*5*7 |
| 701 | Primzahl |
| 702 | 2*3*3*3*13 |
| 703 | 19*37 |
| 704 | 2*2*2*2*2*2*11 |
| 705 | 3*5*47 |
| 706 | 2*353 |
| 707 | 7*101 |
| 708 | 2*2*3*59 |
| 709 | Primzahl |
| 710 | 2*5*71 |
| 711 | 3*3*79 |
| 712 | 2*2*2*89 |
| 713 | 23*31 |
| 714 | 2*3*7*17 |
| 715 | 5*11*13 |
| 716 | 2*2*179 |
| 717 | 3*239 |
| 718 | 2*359 |
| 719 | Primzahl |
| 720 | 2*2*2*2*3*3*5 |
| 721 | 7*103 |
| 722 | 2*19*19 |
| 723 | 3*241 |
| 724 | 2*2*181 |
| 725 | 5*5*29 |
| 726 | 2*3*11*11 |
| 727 | Primzahl |
| 728 | 2*2*2*7*13 |
| 729 | 3*3*3*3*3*3 |
| 730 | 2*5*73 |
| 731 | 17*43 |
| 732 | 2*2*3*61 |
| 733 | Primzahl |
| 734 | 2*367 |
| 735 | 3*5*7*7 |
| 736 | 2*2*2*2*2*23 |
| 737 | 11*67 |
| 738 | 2*3*3*41 |
| 739 | Primzahl |
| 740 | 2*2*5*37 |
| 741 | 3*13*19 |
| 742 | 2*7*53 |
| 743 | Primzahl |
| 744 | 2*2*2*3*31 |
| 745 | 5*149 |
| 746 | 2*373 |
| 747 | 3*3*83 |
| 748 | 2*2*11*17 |
| 749 | 7*107 |
| 750 | 2*3*5*5*5 |
| 751 | Primzahl |
| 752 | 2*2*2*2*47 |
| 753 | 3*251 |
| 754 | 2*13*29 |
| 755 | 5*151 |
| 756 | 2*2*3*3*3*7 |
| 757 | Primzahl |
| 758 | 2*379 |
| 759 | 3*11*23 |
| 760 | 2*2*2*5*19 |
| 761 | Primzahl |
| 762 | 2*3*127 |
| 763 | 7*109 |
| 764 | 2*2*191 |
| 765 | 3*3*5*17 |
| 766 | 2*383 |
| 767 | 13*59 |
| 768 | 2*2*2*2*2*2*2*2*3 |
| 769 | Primzahl |
| 770 | 2*5*7*11 |
| 771 | 3*257 |
| 772 | 2*2*193 |
| 773 | Primzahl |
| 774 | 2*3*3*43 |
| 775 | 5*5*31 |
| 776 | 2*2*2*97 |
| 777 | 3*7*37 |
| 778 | 2*389 |
| 779 | 19*41 |
| 780 | 2*2*3*5*13 |
| 781 | 11*71 |
| 782 | 2*17*23 |
| 783 | 3*3*3*29 |
| 784 | 2*2*2*2*7*7 |
| 785 | 5*157 |
| 786 | 2*3*131 |
| 787 | Primzahl |
| 788 | 2*2*197 |
| 789 | 3*263 |
| 790 | 2*5*79 |
| 791 | 7*113 |
| 792 | 2*2*2*3*3*11 |
| 793 | 13*61 |
| 794 | 2*397 |
| 795 | 3*5*53 |
| 796 | 2*2*199 |
| 797 | Primzahl |
| 798 | 2*3*7*19 |
| 799 | 17*47 |
| 800 | 2*2*2*2*2*5*5 |
| 801 | 3*3*89 |
| 802 | 2*401 |
| 803 | 11*73 |
| 804 | 2*2*3*67 |
| 805 | 5*7*23 |
| 806 | 2*13*31 |
| 807 | 3*269 |
| 808 | 2*2*2*101 |
| 809 | Primzahl |
| 810 | 2*3*3*3*3*5 |
| 811 | Primzahl |
| 812 | 2*2*7*29 |
| 813 | 3*271 |
| 814 | 2*11*37 |
| 815 | 5*163 |
| 816 | 2*2*2*2*3*17 |
| 817 | 19*43 |
| 818 | 2*409 |
| 819 | 3*3*7*13 |
| 820 | 2*2*5*41 |
| 821 | Primzahl |
| 822 | 2*3*137 |
| 823 | Primzahl |
| 824 | 2*2*2*103 |
| 825 | 3*5*5*11 |
| 826 | 2*7*59 |
| 827 | Primzahl |
| 828 | 2*2*3*3*23 |
| 829 | Primzahl |
| 830 | 2*5*83 |
| 831 | 3*277 |
| 832 | 2*2*2*2*2*2*13 |
| 833 | 7*7*17 |
| 834 | 2*3*139 |
| 835 | 5*167 |
| 836 | 2*2*11*19 |
| 837 | 3*3*3*31 |
| 838 | 2*419 |
| 839 | Primzahl |
| 840 | 2*2*2*3*5*7 |
| 841 | 29*29 |
| 842 | 2*421 |
| 843 | 3*281 |
| 844 | 2*2*211 |
| 845 | 5*13*13 |
| 846 | 2*3*3*47 |
| 847 | 7*11*11 |
| 848 | 2*2*2*2*53 |
| 849 | 3*283 |
| 850 | 2*5*5*17 |
| 851 | 23*37 |
| 852 | 2*2*3*71 |
| 853 | Primzahl |
| 854 | 2*7*61 |
| 855 | 3*3*5*19 |
| 856 | 2*2*2*107 |
| 857 | Primzahl |
| 858 | 2*3*11*13 |
| 859 | Primzahl |
| 860 | 2*2*5*43 |
| 861 | 3*7*41 |
| 862 | 2*431 |
| 863 | Primzahl |
| 864 | 2*2*2*2*2*3*3*3 |
| 865 | 5*173 |
| 866 | 2*433 |
| 867 | 3*17*17 |
| 868 | 2*2*7*31 |
| 869 | 11*79 |
| 870 | 2*3*5*29 |
| 871 | 13*67 |
| 872 | 2*2*2*109 |
| 873 | 3*3*97 |
| 874 | 2*19*23 |
| 875 | 5*5*5*7 |
| 876 | 2*2*3*73 |
| 877 | Primzahl |
| 878 | 2*439 |
| 879 | 3*293 |
| 880 | 2*2*2*2*5*11 |
| 881 | Primzahl |
| 882 | 2*3*3*7*7 |
| 883 | Primzahl |
| 884 | 2*2*13*17 |
| 885 | 3*5*59 |
| 886 | 2*443 |
| 887 | Primzahl |
| 888 | 2*2*2*3*37 |
| 889 | 7*127 |
| 890 | 2*5*89 |
| 891 | 3*3*3*3*11 |
| 892 | 2*2*223 |
| 893 | 19*47 |
| 894 | 2*3*149 |
| 895 | 5*179 |
| 896 | 2*2*2*2*2*2*2*7 |
| 897 | 3*13*23 |
| 898 | 2*449 |
| 899 | 29*31 |
| 900 | 2*2*3*3*5*5 |
| 901 | 17*53 |
| 902 | 2*11*41 |
| 903 | 3*7*43 |
| 904 | 2*2*2*113 |
| 905 | 5*181 |
| 906 | 2*3*151 |
| 907 | Primzahl |
| 908 | 2*2*227 |
| 909 | 3*3*101 |
| 910 | 2*5*7*13 |
| 911 | Primzahl |
| 912 | 2*2*2*2*3*19 |
| 913 | 11*83 |
| 914 | 2*457 |
| 915 | 3*5*61 |
| 916 | 2*2*229 |
| 917 | 7*131 |
| 918 | 2*3*3*3*17 |
| 919 | Primzahl |
| 920 | 2*2*2*5*23 |
| 921 | 3*307 |
| 922 | 2*461 |
| 923 | 13*71 |
| 924 | 2*2*3*7*11 |
| 925 | 5*5*37 |
| 926 | 2*463 |
| 927 | 3*3*103 |
| 928 | 2*2*2*2*2*29 |
| 929 | Primzahl |
| 930 | 2*3*5*31 |
| 931 | 7*7*19 |
| 932 | 2*2*233 |
| 933 | 3*311 |
| 934 | 2*467 |
| 935 | 5*11*17 |
| 936 | 2*2*2*3*3*13 |
| 937 | Primzahl |
| 938 | 2*7*67 |
| 939 | 3*313 |
| 940 | 2*2*5*47 |
| 941 | Primzahl |
| 942 | 2*3*157 |
| 943 | 23*41 |
| 944 | 2*2*2*2*59 |
| 945 | 3*3*3*5*7 |
| 946 | 2*11*43 |
| 947 | Primzahl |
| 948 | 2*2*3*79 |
| 949 | 13*73 |
| 950 | 2*5*5*19 |
| 951 | 3*317 |
| 952 | 2*2*2*7*17 |
| 953 | Primzahl |
| 954 | 2*3*3*53 |
| 955 | 5*191 |
| 956 | 2*2*239 |
| 957 | 3*11*29 |
| 958 | 2*479 |
| 959 | 7*137 |
| 960 | 2*2*2*2*2*2*3*5 |
| 961 | 31*31 |
| 962 | 2*13*37 |
| 963 | 3*3*107 |
| 964 | 2*2*241 |
| 965 | 5*193 |
| 966 | 2*3*7*23 |
| 967 | Primzahl |
| 968 | 2*2*2*11*11 |
| 969 | 3*17*19 |
| 970 | 2*5*97 |
| 971 | Primzahl |
| 972 | 2*2*3*3*3*3*3 |
| 973 | 7*139 |
| 974 | 2*487 |
| 975 | 3*5*5*13 |
| 976 | 2*2*2*2*61 |
| 977 | Primzahl |
| 978 | 2*3*163 |
| 979 | 11*89 |
| 980 | 2*2*5*7*7 |
| 981 | 3*3*109 |
| 982 | 2*491 |
| 983 | Primzahl |
| 984 | 2*2*2*3*41 |
| 985 | 5*197 |
| 986 | 2*17*29 |
| 987 | 3*7*47 |
| 988 | 2*2*13*19 |
| 989 | 23*43 |
| 990 | 2*3*3*5*11 |
| 991 | Primzahl |
| 992 | 2*2*2*2*2*31 |
| 993 | 3*331 |
| 994 | 2*7*71 |
| 995 | 5*199 |
| 996 | 2*2*3*83 |
| 997 | Primzahl |
| 998 | 2*499 |
| 999 | 3*3*3*37 |
| 1000 | 2*2*2*5*5*5 |
| 1001 | 7*11*13 |
| 1002 | 2*3*167 |
| 1003 | 17*59 |
| 1004 | 2*2*251 |
| 1005 | 3*5*67 |
| 1006 | 2*503 |
| 1007 | 19*53 |
| 1008 | 2*2*2*2*3*3*7 |
| 1009 | Primzahl |
| 1010 | 2*5*101 |
| 1011 | 3*337 |
| 1012 | 2*2*11*23 |
| 1013 | Primzahl |
| 1014 | 2*3*13*13 |
| 1015 | 5*7*29 |
| 1016 | 2*2*2*127 |
| 1017 | 3*3*113 |
| 1018 | 2*509 |
| 1019 | Primzahl |
| 1020 | 2*2*3*5*17 |
| 1021 | Primzahl |
| 1022 | 2*7*73 |
| 1023 | 3*11*31 |
| 1024 | 2*2*2*2*2*2*2*2*2*2 |
| 1025 | 5*5*41 |
| 1026 | 2*3*3*3*19 |
| 1027 | 13*79 |
| 1028 | 2*2*257 |
| 1029 | 3*7*7*7 |
| 1030 | 2*5*103 |
| 1031 | Primzahl |
| 1032 | 2*2*2*3*43 |
| 1033 | Primzahl |
| 1034 | 2*11*47 |
| 1035 | 3*3*5*23 |
| 1036 | 2*2*7*37 |
| 1037 | 17*61 |
| 1038 | 2*3*173 |
| 1039 | Primzahl |
| 1040 | 2*2*2*2*5*13 |
| 1041 | 3*347 |
| 1042 | 2*521 |
| 1043 | 7*149 |
| 1044 | 2*2*3*3*29 |
| 1045 | 5*11*19 |
| 1046 | 2*523 |
| 1047 | 3*349 |
| 1048 | 2*2*2*131 |
| 1049 | Primzahl |
| 1050 | 2*3*5*5*7 |
| 1051 | Primzahl |
| 1052 | 2*2*263 |
| 1053 | 3*3*3*3*13 |
| 1054 | 2*17*31 |
| 1055 | 5*211 |
| 1056 | 2*2*2*2*2*3*11 |
| 1057 | 7*151 |
| 1058 | 2*23*23 |
| 1059 | 3*353 |
| 1060 | 2*2*5*53 |
| 1061 | Primzahl |
| 1062 | 2*3*3*59 |
| 1063 | Primzahl |
| 1064 | 2*2*2*7*19 |
| 1065 | 3*5*71 |
| 1066 | 2*13*41 |
| 1067 | 11*97 |
| 1068 | 2*2*3*89 |
| 1069 | Primzahl |
| 1070 | 2*5*107 |
| 1071 | 3*3*7*17 |
| 1072 | 2*2*2*2*67 |
| 1073 | 29*37 |
| 1074 | 2*3*179 |
| 1075 | 5*5*43 |
| 1076 | 2*2*269 |
| 1077 | 3*359 |
| 1078 | 2*7*7*11 |
| 1079 | 13*83 |
| 1080 | 2*2*2*3*3*3*5 |
| 1081 | 23*47 |
| 1082 | 2*541 |
| 1083 | 3*19*19 |
| 1084 | 2*2*271 |
| 1085 | 5*7*31 |
| 1086 | 2*3*181 |
| 1087 | Primzahl |
| 1088 | 2*2*2*2*2*2*17 |
| 1089 | 3*3*11*11 |
| 1090 | 2*5*109 |
| 1091 | Primzahl |
| 1092 | 2*2*3*7*13 |
| 1093 | Primzahl |
| 1094 | 2*547 |
| 1095 | 3*5*73 |
| 1096 | 2*2*2*137 |
| 1097 | Primzahl |
| 1098 | 2*3*3*61 |
| 1099 | 7*157 |
| 1100 | 2*2*5*5*11 |
| 1101 | 3*367 |
| 1102 | 2*19*29 |
| 1103 | Primzahl |
| 1104 | 2*2*2*2*3*23 |
| 1105 | 5*13*17 |
| 1106 | 2*7*79 |
| 1107 | 3*3*3*41 |
| 1108 | 2*2*277 |
| 1109 | Primzahl |
| 1110 | 2*3*5*37 |
| 1111 | 11*101 |
| 1112 | 2*2*2*139 |
| 1113 | 3*7*53 |
| 1114 | 2*557 |
| 1115 | 5*223 |
| 1116 | 2*2*3*3*31 |
| 1117 | Primzahl |
| 1118 | 2*13*43 |
| 1119 | 3*373 |
| 1120 | 2*2*2*2*2*5*7 |
| 1121 | 19*59 |
| 1122 | 2*3*11*17 |
| 1123 | Primzahl |
| 1124 | 2*2*281 |
| 1125 | 3*3*5*5*5 |
| 1126 | 2*563 |
| 1127 | 7*7*23 |
| 1128 | 2*2*2*3*47 |
| 1129 | Primzahl |
| 1130 | 2*5*113 |
| 1131 | 3*13*29 |
| 1132 | 2*2*283 |
| 1133 | 11*103 |
| 1134 | 2*3*3*3*3*7 |
| 1135 | 5*227 |
| 1136 | 2*2*2*2*71 |
| 1137 | 3*379 |
| 1138 | 2*569 |
| 1139 | 17*67 |
| 1140 | 2*2*3*5*19 |
| 1141 | 7*163 |
| 1142 | 2*571 |
| 1143 | 3*3*127 |
| 1144 | 2*2*2*11*13 |
| 1145 | 5*229 |
| 1146 | 2*3*191 |
| 1147 | 31*37 |
| 1148 | 2*2*7*41 |
| 1149 | 3*383 |
| 1150 | 2*5*5*23 |
| 1151 | Primzahl |
| 1152 | 2*2*2*2*2*2*2*3*3 |
| 1153 | Primzahl |
| 1154 | 2*577 |
| 1155 | 3*5*7*11 |
| 1156 | 2*2*17*17 |
| 1157 | 13*89 |
| 1158 | 2*3*193 |
| 1159 | 19*61 |
| 1160 | 2*2*2*5*29 |
| 1161 | 3*3*3*43 |
| 1162 | 2*7*83 |
| 1163 | Primzahl |
| 1164 | 2*2*3*97 |
| 1165 | 5*233 |
| 1166 | 2*11*53 |
| 1167 | 3*389 |
| 1168 | 2*2*2*2*73 |
| 1169 | 7*167 |
| 1170 | 2*3*3*5*13 |
| 1171 | Primzahl |
| 1172 | 2*2*293 |
| 1173 | 3*17*23 |
| 1174 | 2*587 |
| 1175 | 5*5*47 |
| 1176 | 2*2*2*3*7*7 |
| 1177 | 11*107 |
| 1178 | 2*19*31 |
| 1179 | 3*3*131 |
| 1180 | 2*2*5*59 |
| 1181 | Primzahl |
| 1182 | 2*3*197 |
| 1183 | 7*13*13 |
| 1184 | 2*2*2*2*2*37 |
| 1185 | 3*5*79 |
| 1186 | 2*593 |
| 1187 | Primzahl |
| 1188 | 2*2*3*3*3*11 |
| 1189 | 29*41 |
| 1190 | 2*5*7*17 |
| 1191 | 3*397 |
| 1192 | 2*2*2*149 |
| 1193 | Primzahl |
| 1194 | 2*3*199 |
| 1195 | 5*239 |
| 1196 | 2*2*13*23 |
| 1197 | 3*3*7*19 |
| 1198 | 2*599 |
| 1199 | 11*109 |
| 1200 | 2*2*2*2*3*5*5 |
| 1201 | Primzahl |
| 1202 | 2*601 |
| 1203 | 3*401 |
| 1204 | 2*2*7*43 |
| 1205 | 5*241 |
| 1206 | 2*3*3*67 |
| 1207 | 17*71 |
| 1208 | 2*2*2*151 |
| 1209 | 3*13*31 |
| 1210 | 2*5*11*11 |
| 1211 | 7*173 |
| 1212 | 2*2*3*101 |
| 1213 | Primzahl |
| 1214 | 2*607 |
| 1215 | 3*3*3*3*3*5 |
| 1216 | 2*2*2*2*2*2*19 |
| 1217 | Primzahl |
| 1218 | 2*3*7*29 |
| 1219 | 23*53 |
| 1220 | 2*2*5*61 |
| 1221 | 3*11*37 |
| 1222 | 2*13*47 |
| 1223 | Primzahl |
| 1224 | 2*2*2*3*3*17 |
| 1225 | 5*5*7*7 |
| 1226 | 2*613 |
| 1227 | 3*409 |
| 1228 | 2*2*307 |
| 1229 | Primzahl |
| 1230 | 2*3*5*41 |
| 1231 | Primzahl |
| 1232 | 2*2*2*2*7*11 |
| 1233 | 3*3*137 |
| 1234 | 2*617 |
| 1235 | 5*13*19 |
| 1236 | 2*2*3*103 |
| 1237 | Primzahl |
| 1238 | 2*619 |
| 1239 | 3*7*59 |
| 1240 | 2*2*2*5*31 |
| 1241 | 17*73 |
| 1242 | 2*3*3*3*23 |
| 1243 | 11*113 |
| 1244 | 2*2*311 |
| 1245 | 3*5*83 |
| 1246 | 2*7*89 |
| 1247 | 29*43 |
| 1248 | 2*2*2*2*2*3*13 |
| 1249 | Primzahl |
| 1250 | 2*5*5*5*5 |
| 1251 | 3*3*139 |
| 1252 | 2*2*313 |
| 1253 | 7*179 |
| 1254 | 2*3*11*19 |
| 1255 | 5*251 |
| 1256 | 2*2*2*157 |
| 1257 | 3*419 |
| 1258 | 2*17*37 |
| 1259 | Primzahl |
| 1260 | 2*2*3*3*5*7 |
| 1261 | 13*97 |
| 1262 | 2*631 |
| 1263 | 3*421 |
| 1264 | 2*2*2*2*79 |
| 1265 | 5*11*23 |
| 1266 | 2*3*211 |
| 1267 | 7*181 |
| 1268 | 2*2*317 |
| 1269 | 3*3*3*47 |
| 1270 | 2*5*127 |
| 1271 | 31*41 |
| 1272 | 2*2*2*3*53 |
| 1273 | 19*67 |
| 1274 | 2*7*7*13 |
| 1275 | 3*5*5*17 |
| 1276 | 2*2*11*29 |
| 1277 | Primzahl |
| 1278 | 2*3*3*71 |
| 1279 | Primzahl |
| 1280 | 2*2*2*2*2*2*2*2*5 |
| 1281 | 3*7*61 |
| 1282 | 2*641 |
| 1283 | Primzahl |
| 1284 | 2*2*3*107 |
| 1285 | 5*257 |
| 1286 | 2*643 |
| 1287 | 3*3*11*13 |
| 1288 | 2*2*2*7*23 |
| 1289 | Primzahl |
| 1290 | 2*3*5*43 |
| 1291 | Primzahl |
| 1292 | 2*2*17*19 |
| 1293 | 3*431 |
| 1294 | 2*647 |
| 1295 | 5*7*37 |
| 1296 | 2*2*2*2*3*3*3*3 |
| 1297 | Primzahl |
| 1298 | 2*11*59 |
| 1299 | 3*433 |
| 1300 | 2*2*5*5*13 |
| 1301 | Primzahl |
| 1302 | 2*3*7*31 |
| 1303 | Primzahl |
| 1304 | 2*2*2*163 |
| 1305 | 3*3*5*29 |
| 1306 | 2*653 |
| 1307 | Primzahl |
| 1308 | 2*2*3*109 |
| 1309 | 7*11*17 |
| 1310 | 2*5*131 |
| 1311 | 3*19*23 |
| 1312 | 2*2*2*2*2*41 |
| 1313 | 13*101 |
| 1314 | 2*3*3*73 |
| 1315 | 5*263 |
| 1316 | 2*2*7*47 |
| 1317 | 3*439 |
| 1318 | 2*659 |
| 1319 | Primzahl |
| 1320 | 2*2*2*3*5*11 |
| 1321 | Primzahl |
| 1322 | 2*661 |
| 1323 | 3*3*3*7*7 |
| 1324 | 2*2*331 |
| 1325 | 5*5*53 |
| 1326 | 2*3*13*17 |
| 1327 | Primzahl |
| 1328 | 2*2*2*2*83 |
| 1329 | 3*443 |
| 1330 | 2*5*7*19 |
| 1331 | 11*11*11 |
| 1332 | 2*2*3*3*37 |
| 1333 | 31*43 |
| 1334 | 2*23*29 |
| 1335 | 3*5*89 |
| 1336 | 2*2*2*167 |
| 1337 | 7*191 |
| 1338 | 2*3*223 |
| 1339 | 13*103 |
| 1340 | 2*2*5*67 |
| 1341 | 3*3*149 |
| 1342 | 2*11*61 |
| 1343 | 17*79 |
| 1344 | 2*2*2*2*2*2*3*7 |
| 1345 | 5*269 |
| 1346 | 2*673 |
| 1347 | 3*449 |
| 1348 | 2*2*337 |
| 1349 | 19*71 |
| 1350 | 2*3*3*3*5*5 |
| 1351 | 7*193 |
| 1352 | 2*2*2*13*13 |
| 1353 | 3*11*41 |
| 1354 | 2*677 |
| 1355 | 5*271 |
| 1356 | 2*2*3*113 |
| 1357 | 23*59 |
| 1358 | 2*7*97 |
| 1359 | 3*3*151 |
| 1360 | 2*2*2*2*5*17 |
| 1361 | Primzahl |
| 1362 | 2*3*227 |
| 1363 | 29*47 |
| 1364 | 2*2*11*31 |
| 1365 | 3*5*7*13 |
| 1366 | 2*683 |
| 1367 | Primzahl |
| 1368 | 2*2*2*3*3*19 |
| 1369 | 37*37 |
| 1370 | 2*5*137 |
| 1371 | 3*457 |
| 1372 | 2*2*7*7*7 |
| 1373 | Primzahl |
| 1374 | 2*3*229 |
| 1375 | 5*5*5*11 |
| 1376 | 2*2*2*2*2*43 |
| 1377 | 3*3*3*3*17 |
| 1378 | 2*13*53 |
| 1379 | 7*197 |
| 1380 | 2*2*3*5*23 |
| 1381 | Primzahl |
| 1382 | 2*691 |
| 1383 | 3*461 |
| 1384 | 2*2*2*173 |
| 1385 | 5*277 |
| 1386 | 2*3*3*7*11 |
| 1387 | 19*73 |
| 1388 | 2*2*347 |
| 1389 | 3*463 |
| 1390 | 2*5*139 |
| 1391 | 13*107 |
| 1392 | 2*2*2*2*3*29 |
| 1393 | 7*199 |
| 1394 | 2*17*41 |
| 1395 | 3*3*5*31 |
| 1396 | 2*2*349 |
| 1397 | 11*127 |
| 1398 | 2*3*233 |
| 1399 | Primzahl |
| 1400 | 2*2*2*5*5*7 |
| 1401 | 3*467 |
| 1402 | 2*701 |
| 1403 | 23*61 |
| 1404 | 2*2*3*3*3*13 |
| 1405 | 5*281 |
| 1406 | 2*19*37 |
| 1407 | 3*7*67 |
| 1408 | 2*2*2*2*2*2*2*11 |
| 1409 | Primzahl |
| 1410 | 2*3*5*47 |
| 1411 | 17*83 |
| 1412 | 2*2*353 |
| 1413 | 3*3*157 |
| 1414 | 2*7*101 |
| 1415 | 5*283 |
| 1416 | 2*2*2*3*59 |
| 1417 | 13*109 |
| 1418 | 2*709 |
| 1419 | 3*11*43 |
| 1420 | 2*2*5*71 |
| 1421 | 7*7*29 |
| 1422 | 2*3*3*79 |
| 1423 | Primzahl |
| 1424 | 2*2*2*2*89 |
| 1425 | 3*5*5*19 |
| 1426 | 2*23*31 |
| 1427 | Primzahl |
| 1428 | 2*2*3*7*17 |
| 1429 | Primzahl |
| 1430 | 2*5*11*13 |
| 1431 | 3*3*3*53 |
| 1432 | 2*2*2*179 |
| 1433 | Primzahl |
| 1434 | 2*3*239 |
| 1435 | 5*7*41 |
| 1436 | 2*2*359 |
| 1437 | 3*479 |
| 1438 | 2*719 |
| 1439 | Primzahl |
| 1440 | 2*2*2*2*2*3*3*5 |
| 1441 | 11*131 |
| 1442 | 2*7*103 |
| 1443 | 3*13*37 |
| 1444 | 2*2*19*19 |
| 1445 | 5*17*17 |
| 1446 | 2*3*241 |
| 1447 | Primzahl |
| 1448 | 2*2*2*181 |
| 1449 | 3*3*7*23 |
| 1450 | 2*5*5*29 |
| 1451 | Primzahl |
| 1452 | 2*2*3*11*11 |
| 1453 | Primzahl |
| 1454 | 2*727 |
| 1455 | 3*5*97 |
| 1456 | 2*2*2*2*7*13 |
| 1457 | 31*47 |
| 1458 | 2*3*3*3*3*3*3 |
| 1459 | Primzahl |
| 1460 | 2*2*5*73 |
| 1461 | 3*487 |
| 1462 | 2*17*43 |
| 1463 | 7*11*19 |
| 1464 | 2*2*2*3*61 |
| 1465 | 5*293 |
| 1466 | 2*733 |
| 1467 | 3*3*163 |
| 1468 | 2*2*367 |
| 1469 | 13*113 |
| 1470 | 2*3*5*7*7 |
| 1471 | Primzahl |
| 1472 | 2*2*2*2*2*2*23 |
| 1473 | 3*491 |
| 1474 | 2*11*67 |
| 1475 | 5*5*59 |
| 1476 | 2*2*3*3*41 |
| 1477 | 7*211 |
| 1478 | 2*739 |
| 1479 | 3*17*29 |
| 1480 | 2*2*2*5*37 |
| 1481 | Primzahl |
| 1482 | 2*3*13*19 |
| 1483 | Primzahl |
| 1484 | 2*2*7*53 |
| 1485 | 3*3*3*5*11 |
| 1486 | 2*743 |
| 1487 | Primzahl |
| 1488 | 2*2*2*2*3*31 |
| 1489 | Primzahl |
| 1490 | 2*5*149 |
| 1491 | 3*7*71 |
| 1492 | 2*2*373 |
| 1493 | Primzahl |
| 1494 | 2*3*3*83 |
| 1495 | 5*13*23 |
| 1496 | 2*2*2*11*17 |
| 1497 | 3*499 |
| 1498 | 2*7*107 |
| 1499 | Primzahl |
| 1500 | 2*2*3*5*5*5 |
Mersenne Zahlen - Mersennsche Zahlen - Mersenne Primzahlen
Eine Mersennesche Zahl ist eine Zahl der Form 2n-1. Die Primzahlen unter den Mersenne-Zahlen werden als Mersenne-Primzahlen bezeichnet.
Nachfolgend aufgeführt ist die Liste aller bislang bekannten Mersenne-Primzahlen.
| Nr. | Exponent p | Ziffern | Jahr | Entdecker |
|---|---|---|---|---|
| 1 | 2 | 1 | - | - |
| 2 | 3 | 1 | - | - |
| 3 | 5 | 2 | - | - |
| 4 | 7 | 3 | - | - |
| 5 | 13 | 4 | 1456 | unbekannt |
| 6 | 17 | 6 | 1588 | Cataldi |
| 7 | 19 | 6 | 1588 | Cataldi |
| 8 | 31 | 10 | 1772 | Euler |
| 9 | 61 | 19 | 1883 | Pervushin |
| 10 | 89 | 27 | 1911 | Powers |
| 11 | 107 | 33 | 1914 | Powers |
| 12 | 127 | 39 | 1876 | Lucas |
| 13 | 521 | 157 | 1952 | Robinson |
| 14 | 607 | 183 | 1952 | Robinson |
| 15 | 1279 | 386 | 1952 | Robinson |
| 16 | 2203 | 664 | 1952 | Robinson |
| 17 | 2281 | 687 | 1952 | Robinson |
| 18 | 3217 | 969 | 1957 | Riesel |
| 19 | 4253 | 1281 | 1961 | Hurwitz |
| 20 | 4423 | 1332 | 1961 | Hurwitz |
| 21 | 9689 | 2917 | 1963 | Gillies |
| 22 | 9941 | 2993 | 1963 | Gillies |
| 23 | 11213 | 3376 | 1963 | Gillies |
| 24 | 19937 | 6002 | 1971 | Tuckerman |
| 25 | 21701 | 6533 | 1978 | Noll, Nickel |
| 26 | 23209 | 6987 | 1979 | Noll |
| 27 | 44497 | 13395 | 1979 | Nelson, Slowinski |
| 28 | 86243 | 25962 | 1982 | Slowinski |
| 29 | 110503 | 33265 | 1988 | Colquitt, Welsh |
| 30 | 132049 | 39751 | 1983 | Slowinski |
| 31 | 216091 | 65050 | 1985 | Slowinski |
| 32 | 756839 | 227832 | 1992 | Slowinski, Gage |
| 33 | 859433 | 258716 | 1994 | Slowinski, Gage |
| 34 | 1257787 | 378632 | 1996 | Slowinski, Gage |
| 35 | 1398269 | 420921 | 1996 | Armengaud, Woltman u. a. (GIMPS) |
| 36 | 2976221 | 895932 | 1997 | Spence, Woltman u. a. (GIMPS) |
| 37 | 3021377 | 909526 | 1998 | Clarkson, Woltman, Kurowski u. a. (GIMPS, PrimeNet) |
| 38 | 6972593 | 2098960 | 1999 | Hajratwala, Woltman, Kurowski u. a. (GIMPS, PrimeNet) |
| 39 | 13466917 | 4053946 | 2001 | Cameron, Woltman, Kurowski u. a. (GIMPS, PrimeNet) |
| 40 | 20996011 | 6320430 | 2003 | Shafer, Woltman, Kurowski u. a. (GIMPS, PrimeNet) |
| 41 | 24036583 | 7235733 | 2004 | Findley, Woltman, Kurowski u. a. (GIMPS, PrimeNet) |
| 42 | 25964951 | 7816230 | 2005 | Nowak, Woltman, Kurowski u. a. (GIMPS, PrimeNet) |
| 43 | 30402457 | 9152052 | 2005 | Cooper, Boone, u. a. (GIMPS, PrimeNet) |
| 44 | 32582657 | 9808358 | 2006 | Cooper, Boone, u. a. (GIMPS, PrimeNet) |
| 45 | 37156667 | 11185272 | 2008 | Elvenich, Woltman, Kurowski, u. a. (GIMPS, PrimeNet) |
| 46 * | 43112609 | 12978189 | 2008 | Smith, Woltman, Kurowski, u. a. (GIMPS, PrimeNet) |
| 47 * | 42643801 | 12837064 | 2009 | Odd Magnar Strinmo, Melhus (GIMPS, PrimeNet) |
| 48 * | 57885161 | 17425170 | 2013 | Cooper, u. a. (GIMPS, PrimeNet) |
| 49 * | 74207281 | 22338618 | 2016 | Cooper, u. a. (GIMPS, PrimeNet) |
| 50 * | 77232917 | 23249425 | 2017 | Jonathan Pace (GIMPS, PrimeNet) |
| 51 * | 82589933 | 24862048 | 2018 | Patrick Laroche (GIMPS, PrimeNet) |
Bei den mit * gekennzeichneten Zahlen handelt es sich um Mersenne-Primzahlen deren Existenz noch nicht bewiesen ist.
Quelle: Wikipedia - Mersennesche Zahlen
Berechnung - Nutzung dieses Moduls
Um mit diesem Modul Untersuchungen zum entsprechenden Themengebiet durchzuführen, wählen Sie zunächst den hierfür relevanten Eintrag aus der aufklappbaren Auswahlbox und legen durch die Eingabe erforderlicher Werte in die dafür vorgesehenen Felder den zu analysierenden Zahlenwertebereich fest.
Bedienen Sie hierauf die Schaltfläche Berechnen, so werden die Ergebnisse in der dafür zur Verfügung stehenden Tabelle ausgegeben.
Bei der Suche nach Distanz-m-Primzahlen muss der Wert für die geforderte Distanz, innerhalb der sich keine weiteren Primzahlen befinden sollen, im Eingabefeld Distanz m definiert werden.
Die Suche nach Fastprime Zahlen erfordert die Festlegung der Anzahl n der Faktoren, in die eine natürliche Zahl bei derer Primfaktorzerlegung aufgeteilt werden soll. Geben Sie hierfür den entsprechenden Wert in das Feld Grad n ein.
Da es mehrere Möglichkeiten gibt, eine Zahl als Summe von vier Quadratzahlen darzustellen, können Sie durch die Aktivierung des Kontrollschalters Eine Zerlegung bzw. Alle Zerlegungen festlegen, ob lediglich eine dieser ausgegeben werden soll, oder ob Sie alle derer angezeigt bekommen möchten.
Bei der Analyse von Pseudo-Primzahlen ist es erforderlich den Wert für die Basis zu definieren. Legen Sie diesen durch die Eingabe des entsprechenden Werts in das Feld Basis fest.
Vor der Ermittlung von Cunningham-Zahlen muss festgelegt werden, welcher Art die Zahlen der Reihe entsprechen sollen. Aktivieren Sie hierzu den Kontrollschalter Reihen 1. Art, bzw. Reihen 2. Art. Zudem ist die Festlegung einer Mindestreihenlänge erforderlich. Führen Sie diese durch die Eingabe eines entsprechenden Zahlenwerts in das Feld Reihenlänge durch.
Hinweis:
Da die Ermittlung von Primzahlen über einen großen Zahluntersuchungsbereich hinweg sehr zeitaufwändig sein kann, können Sie laufende Berechnungen durch die Bedienung der Taste ESC abbrechen.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Anwendungsaufgaben genutzt werden.
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Weitere Themenbereiche
Sieb des Eratosthenes
Beispiele
Beispiel 1 - Primzahlen:
Wurde der Eintrag Primzahlen gewählt und zur Suche nach Primzahlen ein Bereich zwischen 1 und 15 festgelegt, so gibt das Programm folgende Ergebnisse aus:
Primzahlen: 2; 3; 5; 7; 11; 13
Beispiel 2 - Primzahlzwillinge:
Wurde der Eintrag Primzahlzwillinge gewählt und ein Untersuchungsbereich zwischen 2 und 30 festgelegt, so ermittelt das Programm die Primzahlzwillinge: [3;5]; [5;7]; [11;13]; [17;19]; [29;31].
Beispiel 3 - Primzahlvierlinge:
Wurde der Eintrag Primzahlvierlinge gewählt und ein Untersuchungsbereich zwischen 2 und 200 festgelegt, so ermittelt das Programm die Primzahlvierlinge: [5;7;11;13], [11;13;17;19],[101;103;107;109],[191;193;197;199].
Beispiel 4 - Sexy-Primzahlen:
Wurde der Eintrag Sexy-Primzahlen gewählt und ein Untersuchungsbereich zwischen 1 und 20 festgelegt, so ermittelt das Programm die Primzahlzwillinge: [5;11]; [7;13]; [11;17]; [13;19]; [17;23].
Beispiel 5 - 4n+1-Primzahlen:
Wurde der Eintrag 4n+1-Primzahlen gewählt und ein Untersuchungsbereich zwischen 1 und 40 festgelegt, so ermittelt das Programm die 4n+1-Primzahlen mit: 5 = 1²+2², 13 = 2²+3², 17 = 1²+4², 29 = 2²+5², 37 = 1²+6².
Beispiel 6 - Mirp-Primzahlen:
Wurde der Eintrag Mirp-Primzahlen gewählt und ein Untersuchungsbereich zwischen 1 und 80 festgelegt, so ermittelt das Programm die Mirp-Primzahlen: 11, 13, 17, 31, 37, 71, 73, 79.
Beispiel 7 - Euler-Theorem:
Wurde der Eintrag Euler-Theorem (6n+1) gewählt und ein Untersuchungsbereich zwischen 1 und 50 festgelegt, so ermittelt das Programm die 6n+1-Primzahlen mit: 7 = 2²+3·1², 13 = 1²+3·2², 19 = 4²+3·1², 31 = 2²+3·3², 37 = 5²+3·2², 43 = 4²+3·3².
Beispiel 8 - Primfaktoren - Primfaktorzerlegung:
Wurde der Eintrag Primfaktoren gewählt und gilt es die Primfaktoren aller Zahlen innerhalb eines Bereichs von 100 bis 105 ermitteln zu lassen, so gibt das Programm folgende Ergebnisse aus:
100 = 2·2·2·5
101 Primzahl
103 Primzahl
104 = 2·2·2·13
105 = 3·5·7
Beispiel 9 - Distanz-m-Primzahlen:
Wurde der Eintrag Distanz-m-Primzahlen gewählt, ein Untersuchungsbereich zwischen 1 und 20, sowie eine Distanz von m = 4 festgelegt, so findet das Programm die Distanz-m-Primzahlen: [3;7]; [7;11]; [13;17]; [19;23]; [37;41]; [43;47].
Beispiel 10 - Cousin-Primzahlen:
Wurde der Eintrag Cousin-Primzahlen gewählt und ein Untersuchungsbereich zwischen 1 und 60 festgelegt, so ermittelt das Programm die Cousin-Primzahlen: [7;11]; [13;17]; [19;23]; [37;41]; [43;47].
Beispiel 11 - Gute-Primzahlen:
Wurde der Eintrag Gute-Primzahlen gewählt und ein Untersuchungsbereich zwischen 1 und 60 festgelegt, so ermittelt das Programm als Gute Primzahlen: 11, 17, 29, 37, 41, 53.
Beispiel 12 - Fastprime-Zahlen:
Wurde der Eintrag Fastprime-Zahlen gewählt und ein Untersuchungsbereich zwischen 1 und 300 festgelegt, so ermittelt das Programm die Fastprime-Zahlen: 64 = 2·2·2·2·2·2, 96 = 2·2·2·2·2·3, 144 = 2·2·2·2·3·3, 160 = 2·2·2·2·2·5, 216 = 2·2·2·3·3·3, 224 = 2·2·2·2·2·7, 240 = 2·2·2·2·3·5.
Beispiel 13 - Eulersche Funktion:
Die Zahl 6 ist zu 2 Zahlen zwischen 1 und 6 teilerfremd (1 und 5), somit ist φ(6) = 2. Die Zahl 13 ist als Primzahl zu den 12 Zahlen von 1 bis 12 teilerfremd, somit ist φ(13) = 12.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| φ(n) | 1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | 4 | 10 | 4 | 12 | 6 | 8 |
Beispiel 14 - Vierqauadratesatz nach Lagrange:
Wurde der Eintrag Vierquadratesatz Lagrange gewählt und ein Untersuchungsbereich zwischen 1 und 50 festgelegt, so ermittelt das Programm die Primzahlen: 7 = 2²+1²+1²+1², 11 = 3²+1²+1²+0², 19 = 4²+1²+1²+1², 23 = 3²+3²+2²+1², 31 = 5²+2²+1²+1².
Beispiel 15 - Pseudoprimzahlen:
Wurde der Eintrag Pseudoprimzahlen gewählt, ein Untersuchungsbereich zwischen 1 und 300, sowie eine Basis 11 festgelegt, so ermittelt das Programm die Pseudo-Primzahlen: 15, 70, 133, 190, 259.
Beispiel 16 - Sophie-Primzahlen:
Wurde der Eintrag Sophie-Primzahlen gewählt und ein Untersuchungsbereich zwischen 1 und 50 festgelegt, so gibt das Programm die Sophie-Primzahlen 2, 3, 5, 11, 23, 29, 41 aus.
Beispiel 17 - Cunningham-Primzahlen:
Wurde der Eintrag Cunningham-Primzahlen gewählt, ein Untersuchungsbereich zwischen 1 und 400 festgelegt, eine Reihenlänge von 3 festgelegt, so ermittelt das Programm für Reihen der 1. Art die Tupel [2;3,5], [19;37;73], [79;157;313], [331;661;1321] und für Reihen der 2. Art die Tupel [11;23,47], [41;83;167].
Beispiel 18 - Ruth-Aaron-Paare:
Wurde der Eintrag Ruth-Aaron-Paare gewählt und ein Untersuchungsbereich zwischen 1 und 500 festgelegt, so gibt das Programm die Ruth-Aaron-Paare: [5;6]; [8;9]; [15;16]; [77;78], [125;126] aus.

Beispiel 1 - Primfaktoren

Beispiel 2 - Fastprime-Zahlen

Beispiel 3 - Cunningham-Primzahlen

Beispiel 4 - Cousin-Primzahlen

Beispiel 5 - 4n+1-Primzahlen

Beispiel 6 - Primzahlzwillinge
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Primzahl zu finden.
Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
MathProf 5.0 - Unterprogramm Sieb des Eratosthenes

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















