MathProf - Feigenbaum - Diagramm - Fraktale - Konstante

 

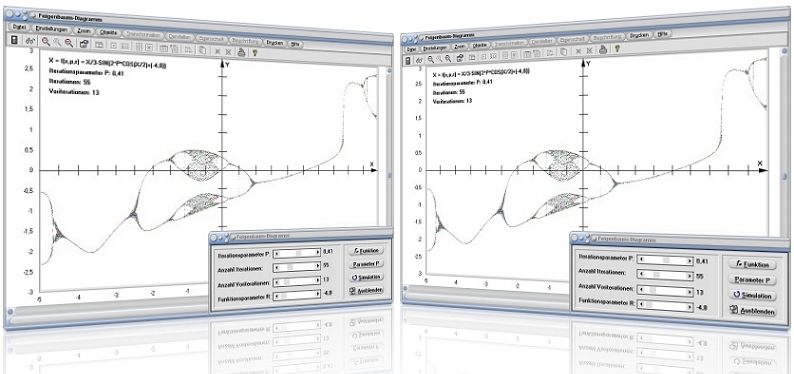
Modul Feigenbaum-Diagramm

---

 
Mit Hilfe des Unterprogramms [Sonstiges] - [Fraktale] - Feigenbaum-Diagramm lassen sich Feigenbaum-Diagramme unter dem Einfluss von Parametern darstellen.

 

Um das chaotische Verhalten einer Funktion f(x,p) zu analysieren, wird über deren Parameter p eine Iteration durchgeführt. Hierunter wird die wiederholte Anwendung derselben Rechenvorschrift verstanden, wobei jedes Berechnungsergebnis als Ausgangswert für die darauffolgende Berechnung dient. Die entsprechende Funktion wird somit mehrfach auf sich selbst angewandt. Dieser Vorgang kann beliebig oft wiederholt werden, wobei die Anzahl durchgeführter Iterationsschritte als Iterationstiefe bezeichnet wird.
 
Ein Endzustand ist häufig erst nach einigen Iterationsschritten (Voriterationen) erkennbar, denn die Anfangsphase, welche als Einschwingphase bezeichnet wird, zeigt in der Regel noch nicht den für die Bahn typischen Verlauf. Werden diese Zusammenhänge grafisch dargestellt, so kann hieraus das Verhalten dieser Funktion entnommen werden. Eine Darstellung dieser Art trägt die Bezeichnung Feigenbaum-Diagramm.

Ein Feigenbaumdiagramm entsteht durch das Aufzeichnen der Wertepaare einer logistischen Gleichung (p,x_n) der Form x_n+1 = p·(1-x_n)·x_n.
 
Zunächst wird eine festgelegte Anzahl n durchzuführender Iterationen festgelegt, die hierauf für alle zu berechnenden Punkte der Diagramms beibehalten wird. Für jeden Wert p wird hierauf eine Reihe von x₀ Startwerten, die zwischen 0 und 1 liegen, zufällig oder in fortlaufender Reihenfolge gewählt. Für alle festgelegten Startwerte werden mit der logistischen Gleichung gemeinsam mit dem festgelegten Wert für p n-malig Iterationen durchgeführt.
 
Für jeden berechneten Wert von x_n wird in der Grafik (dem Diagramm) beim Abszissenwert p ein Punkt dargestellt. Dieser Vorgang wird über den gesamten Wertebereich von p durchgeführt. Jeder der im Diagramm dargestelten Punkte ist somit das Ergebnis einer festgelegten Anzahl von n durchgeführten Iterationen für einen definierten Startwert x₀. In einigen Bereichen des Diagramms in dem einzelne Linienzüge sichtbar sind, konvergieren nahezu alle Startwerte bei p auf die gleichen Endwerte x_n. In Bereichen, bei denen dies nicht zutrifft, verteilen sich diese Endwerte zufällig und es entsteht das charaktistische Bild eines Feigenbaumdiagramms.
 

In dem Bereich, in welchem lediglich ein einzelner Ast zu sehen ist, strebt das Verhalten des Systems gegen einen einzigen Endzustand (Konvergenz). Sind 2, 4 ,6 , 8 .....Äste zu erkennen, so pendelt das Verhalten des Systems zwischen 2, 4 ,6 , 8..... Endzuständen. Diese werden als Perioden bezeichnet. Wird die Intervalllänge, innerhalb welcher eine Periode vorliegt stetig kleiner, so strebt das Verhältnis der Längen zweier aufeinander folgender Äste gegen einen Grenzwert von δ = 4,6692016091029, die Feigenbaumkonstante.

Es handelt sich hierbei um eine Naturkonstante, welche bei vielen physikalischen Prozessen auszumachen ist, deren Verhalten von Konvergenz über Periodizität in Chaos übergeht.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Benutzbarbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens genutzt werden.
 
Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf anschauliche Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthemengebiet.

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Darstellung

 

 

Um mit Hilfe dieses Moduls Analysen zu diesem Fachthema durchzuführen, sollten Sie folgendermaßen vorgehen:
 

1. Definieren Sie die Funktion mit der Zusammenhänge untersucht werden sollen, indem Sie den Schalter fx Funktion bedienen. Geben Sie den entsprechenden Funktionsterm in das Feld mit der Bezeichnung f(x,p,r) = ein und bedienen Sie hierauf die Schaltfläche OK. Beachten Sie hierbei die geltenden Syntaxregeln.
   
   Befinden sich bereits gespeicherte Funktionen in der Bibliothek, so können diese durch einen Doppelklick auf den entsprechenden Eintrag in der Tabelle in das Eingabefeld übernommen werden.
    

2. Legen Sie den Startwert für den Iterationsparameter P durch eine Bedienung des Rollbalkens Iterationsparameter P fest.
    

3. Bestimmen Sie die Anzahl durchzuführender Iterationen bzw. Voriterationen durch eine Bedienung der Schieberegler Anzahl Iterationen bzw. Anzahl Voriterationen.
    

4. Möchten Sie derartige Zusammenhänge unter Einfluss eines Funktionsparameters untersuchen, so besteht die Möglichkeit der entsprechenden Funktion einen Parameter R zu übergeben. Um den zu durchlaufenden Parameterwertebereich dessen festzulegen und die gewünschte Parameterschrittweite zu definieren, bedienen Sie den Schalter Parameter P.
   
   Grundsätzliches bezüglich der Nutzung von Funktionsparametern bei der Darstellung mathematischer Funktionen finden Sie unter Verwendung von Funktionsparametern.
   
   Beachten Sie hierbei, dass in diesem Unterprogramm der Funktionsparameter die Bezeichnung R trägt - und nicht P! Wurde eine Funktion mit Funktionsparameter R definiert, so kann dieser durch eine Positionierung des Rollbalkens Parameter R verändert werden.
    

5. Starten Sie bei Bedarf eine Autosimulation mit dem Schalter Simulation, um die Einflüsse des Iterationsparameters P, bzw. des Funktionsparameters R zu untersuchen und beenden Sie diese wieder durch einen erneuten Klick auf diese Schaltfläche. Vor dem Start einer Simulation wird Ihnen ein Auswahlformular zur Verfügung gestellt, auf welchem Sie durch die Aktivierung des entsprechenden Kontrollschalters eine Auswahl bzgl. der simulativ zu verändernden Größe treffen können. Ebenfalls können Sie hierauf den Wert für die zu verwendende Verzögerung einstellen. Ändern Sie diese bei Bedarf und bestätigen Sie mit OK. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Lindenmeyer-System

Lindenmeyer-System II

 

 

 

Bei Darstellung des Feigenbaum-Diagramms mit den Einstellungen

 

Iterationsparameter: P = -0,8

Iterationen: 100

Voriterationen: 10

 

zur Funktionsgleichung X = f(x,p) = P·X·2^(2·P-1) kann festgestellt werden:

 

Chaotisches Verhalten bis zum Wert x = -3,2

Periodisch konvergentes Verhalten zwischen x = -3,2 und x = -1,2 

Konvergentes Verhalten zwischen x = -1,2 und x = 1,2
 

 

Grafische Darstellung - Beispiel 1
 

Grafische Darstellung - Beispiel 2

  

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Feigenbaumkonstante zu finden.

 

 

Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach

 

MathProf 5.0 - Unterprogramm Pythagoras-Baum

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---