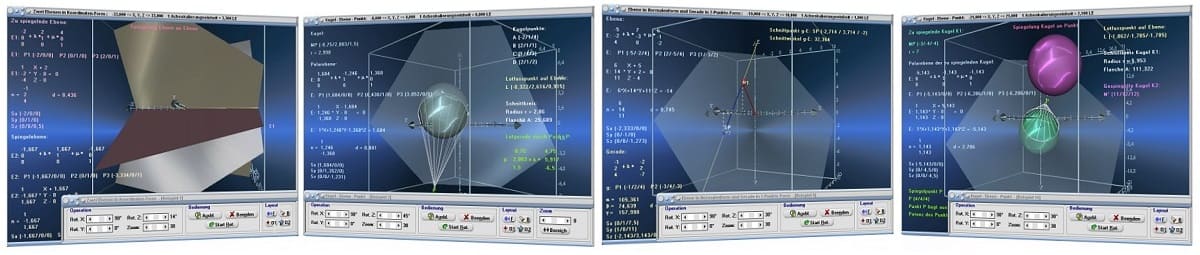
Screenshots zum
Themengebiet Vektoralgebra
Nachfolgend dargestellt sind Screenshots von Beispielen
einiger zu diesem Fachthemengebiet in MathProf 5.0
implementierter Unterprogramme.
finden Sie hier, oder durch die Ausführung eines Klicks auf ein Bild.
Unter dem Programmpunkt [Vektoralgebra] - [Grundlegendes (2D)] - [Vektoraddition in der Ebene} wird die Möglichkeit geboten, sich Zusammenhänge bei der
Addition von Vektoren in der Ebene zu verdeutlichen.
Das Unterprogramm [Vektoralgebra] - [Grundlegendes (2D)] - [Vektorielle Linearkombination] ermöglicht die Analyse der Zusammenhänge bei der Bildung einer
Linearkombination zweier Vektoren in der Ebene.
Das kleine Modul [Vektoralgebra] - [Vektoraddition] - [Grafische Vektoraddition im Raum] ermöglicht die Analyse der Zusammenhänge bei Durchführung einer
Vektoraddition im Raum.
Zwei 3D-Module unter [Vektoralgebra] ermöglichen die Durchführung von verschiedenen Berechnungen sowie grafischen Untersuchungen mit Geraden
im Raum.
Entsprechende Module unter [Vektoralgebra] - [Ebene - Gerade] ermöglichen die numerische Durchführung
relevanter Berechnungen zu diesem Fachthema sowie die grafische Darstellung von Ebenen und Geraden im Raum.
Durch die Verwendung unterschiedlicher Teilprogramme unter [Vektoralgebra] - [Ebene] können Berechnungen und grafische Darstellungen zu Sachverhalten bzgl.
Ebenen und Punkten im Raum durchgeführt bzw. ausgegeben werden.
Mit Hilfe mehrerer Unterprogramme zum Fachthemenbereich [Vektoralgebra] - [Ebene] können Spiegelungen von Ebenen im Raum numerisch und grafisch
durchgeführt werden.
Mit Hilfe mehrerer Module zum Fachthemenbereich [Vektoralgebra] - [Ebene] können Spiegelungen von Ebenen im Raum numerisch und grafisch
durchgeführt werden.
Das Unterprogramm [Vektoralgebra] - [Kugel - Kugel] ermöglicht die Durchführung verschiedener Untersuchungen mit zwei Kugeln im Raum sowie die
Ermittlung und Darstellung ven Schnittebenen derer.
Unter dem Menüeintrag [Vektoralgebra] - [Kugel - Ebene - Punkt] ermöglicht die Durchführung von Untersuchungen
mit Ebenen, Kugeln und Punkten bzgl. verschiedener Sachverhalte.
Im 3D-Modul [Vektoralgebra] - [Kugel - Gerade] können numerische wie grafische Analysen mit Kugeln und Geraden im Raum durchgeführt werden.
Im 3D-Modul [Vektoralgebra] - [Kugel - Gerade] können numerische wie grafische Analysen mit Kugeln und Geraden im Raum durchgeführt werden.
Mit Hilfe des 3D-Moduls [Vektoralgebra] - [Kugel - Ebene - Punkt] können Analysen zu Sachverhallten bzgl. den Positionen von Kugeln und Punkten im
Raum numerisch wie auch grafisch ausgeführt werden.
Im 3D-Teilprogramm [Vektoralgebra] - [Kugel - Ebene - Punkt] können Untersuchungen zu Spiegelungen von Kugeln an Punkten im Raum praktiziert werden.
Das 3D-Modul [Vektoralgebra] - [Kugel - Kugel] ermöglicht die Durchführung verschiedener numerischer wie auch grafischer Untersuchungen mit zwei
Kugeln im Raum.
Das 3D-Modul [Vektoralgebra] - [Kugel - Kugel] ermöglicht die Durchführung verschiedener numerischer wie auch grafischer Untersuchungen mit zwei
Kugeln im Raum.
Zu diesem Fachthemengebiet sind insgesamt 43 Unterprogramme eingebunden.
Gerade und Vektoren - Vektorielle Linearkombination - Vektorielles Teilverhältnis - Vektoraddition in der Ebene - Resultierende - Komponentendarstellung (3D) - Vektorprodukt (3D) - Skalarprodukt (3D) - Spatprodukt (3D) - Vektorprojektion (3D) - Tripelprodukt (3D) - Numerische Vektoraddition im Raum - Grafische Vektoraddition im Raum (3D) - Gerade in Punkt-Richtungs-Form (3D) - Gerade in 2-Punkte-Form (3D) - Ebene in Punkt-Richtungs-Form (3D) - Ebene in 3-Punkte-Form (3D) - Ebene in Normalen-Form (3D) - Ebene in Koordinaten-Form (3D) - Zwei Ebenen (3D) - Kugel - Gerade (3D) - Kugel - Ebene - Punkt (3D) - Kugel - Kugel (3D)
Weitere relevante Seiten zu diesem Programm
 |  |
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Weitere Videos zu einigen in MathProf implementierten Modulen finden Sie, indem Sie den Reiter MathProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Weitere Videos zu einigen in PhysProf implementierten Modulen finden Sie, indem Sie den Reiter PhysProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Weitere Videos zu einigen mit SimPlot erzeugten Animationen finden Sie unter SimPlot-Videos, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
